ABSTRACT
Examining the albedo distribution of the near-Earth object (NEO) population allows for a better understanding of the relationship between absolute (H) magnitude and size, which impacts calculations of the size frequency distribution and impact hazards. Examining NEO albedos also sheds light on the differences between the NEO and Main Belt populations. We combine albedo results from the ExploreNEOs Warm Spitzer Exploration Science program with taxonomic classifications from the literature, publicly available data sets, and new observations from our concurrent spectral survey to derive the average albedos for C-, D-, Q-, S-, V-, and X-complex NEOs. Using a sample size of 118 NEOs, we calculate average albedos of 0.29+0.05−0.04, 0.26+0.04−0.03, and 0.42+0.13−0.11 for the Q-, S-, and V-complexes, respectively. The averages for the C- and D-complexes are 0.13+0.06−0.05 and 0.02+0.02−0.01, but these averages are based on a small number of objects (five and two, respectively) and will improve with additional observations. We use albedos to assign X-complex asteroids to one of the E-, M-, or P-types. Our results demonstrate that the average albedos for the C-, S-, V-, and X-complexes are higher for NEOs than the corresponding averages observed in the Main Belt.
1. INTRODUCTION
For decades, researchers have sought to perfect a classification scheme for asteroids based on the features observed in their reflectance spectra. As a result, several taxonomic systems have emerged, such as those of Tholen (1984), Bus & Binzel (2002a), and DeMeo et al. (2009), each depending in some way on measurements of the spectral slope and absorption features, and enabling basic compositional properties to be inferred if average compositions of the different classes are known. While in some cases a taxonomic classification can suggest the presence of certain minerals, such as silicates, in other cases the mineralogical interpretation is ambiguous. In these cases, albedo measurements are required to break the spectroscopic degeneracy and to more effectively constrain the mineralogy. Accurate albedo measurements alone are not enough to determine composition, but usually exclude certain mineralogies. The combination of a taxonomic classification based on spectral features and measured geometric albedo provides a robust assessment of basic compositional properties and the effects of any surface processing, such as space weathering.
These studies are particularly illuminating for near-Earth objects (NEOs). Investigations of the average albedos of the various taxonomic complexes, as well as the range of albedos within a complex, shed light on the properties of the NEO population and how it differs from other asteroid populations. The factors that most influence the albedo of an object are the bulk composition and the constituent minerals of the object. However, physical properties of an object's surface, such as the degree of space weathering and the grain size distribution, also affect the albedo of an object.
In addition to providing insight into the mineralogies of near-Earth asteroids (NEAs), understanding the albedo distribution and the average albedos of certain populations, such as taxonomic classes, informs our understanding of the NEA population as a whole. Conversions from absolute magnitude (H) to size rely on albedo (Harris & Harris 1997) and are frequently used in determinations of debiased size frequency distributions of NEOs and the related impact risk (Morbidelli et al. 2002; Stuart & Binzel 2004). For many years, these calculations relied on albedo values obtained from studies of the Main Belt population. However, several key differences exist between the Main Belt and near-Earth environments, such as space weathering rates and collisional evolution timescales. Additionally, NEOs are a biased sample of the Main Belt population and have different taxonomic class abundances than the Main Belt. Due to these differences, we do not expect the average albedos of the total NEO population or of the individual taxonomic complexes to be identical to their Main Belt counterparts. Therefore, studies of NEA albedos, such as those done by Delbó et al. (2003) and Stuart & Binzel (2004), are important to our understanding of the NEO population. The more accurate our relationship between H magnitude and object size is, the more accurately we can examine the size distribution of NEOs and the progress toward meeting the Congressional mandate of identifying 90% of NEOs larger than 140 m.12
Stuart & Binzel (2004) calculated debiased average albedos for the C-, D-, O-, Q-, S-, V-, and X-complexes in the NEO population using the albedos of a total of 36 objects within those complexes. Their work demonstrated that for NEOs the average population albedo and the average albedos of some complexes were not equivalent to their corresponding Main Belt averages. For years the average albedo of the NEO population was assumed to be 0.11 (Stuart 2001; Werner et al. 2002), which was the canonical average of the Main Belt population (Ryan & Woodward 2010). Using this average albedo, H = 18 corresponds to a diameter of 1 km. Stuart & Binzel (2004) found a debiased NEO population albedo of 0.14 ± 0.02, which changed the H magnitude of a 1 km object to H = 17.8 ± 0.1. Stuart & Binzel (2004) calculated average Main Belt C-, S-, and X-complex albedos using the values from Tedesco et al. (2002) as 0.06 ± 0.04, 0.20 ± 0.06, and 0.10 ± 0.09, respectively. Debiased albedos for the same complexes in the NEO population were calculated to be 0.101 ± 0.027, 0.238 ± 0.044, and 0.072 ± 0.025, respectively. The C- and S-complex albedos were noticeably higher for NEOs. The X-complex NEO average was consistent with the average and error of the Main Belt calculation. Delbó (2004) also showed evidence of higher albedos in the near-Earth population than in the Main Belt.
Stuart & Binzel (2004) also give a sense of the nominal albedo range expected for each taxonomic complex. The darker complexes show a narrower range of albedos than the high albedo complexes. The C-complex shows a range of albedos from 0.052–0.17, while the Q-, S-, and V-complexes have ranges of 0.14–0.63, 0.15–0.52, and 0.31–0.53, respectively. Since the X-complex is comprised of three types of objects that are only distinguishable when the albedo is known, the wide range of albedos for this complex (0.023–0.55) is expected. Stuart & Binzel (2004) only had a single NEO albedo from the dark D-complex. This value closely matched D-types in Main Belt, which suggested a narrow range of albedos between the two populations.
In this paper, we use results from the ExploreNEOs Warm Spitzer Exploration Science project (Trilling et al. 2010) to investigate the average albedo by spectral complex for 118 NEOs. Section 2 describes the albedos obtained through the ExploreNEOs program and complementary taxonomic classifications from the literature and new observations. Section 3 combines the albedo values and taxonomic classifications to calculate average albedos for the C-, D-, Q-, S-, V-, and X-complexes. We discuss the implications of our results in Section 4.
2. DATA
2.1. Albedos from ExploreNEOs
The albedo values presented here were determined as part of the ExploreNEOs Warm Spitzer Exploration Science project. ExploreNEOs uses the post-cryogenic, or warm, mode of IRAC (Fazio et al. 2004) on the Spitzer Space Telescope (Werner et al. 2004). Thermal modeling using the IRAC fluxes and published H magnitudes for each asteroid yields an estimate of the diameter and albedo.
This is the fifth paper in the ExploreNEOs series. Paper I (Trilling et al. 2010) described the design of the ExploreNEOs program and the thermal modeling procedure in detail. Paper II (Harris et al. 2011) compared initial results with previous ground-based observations to determine the accuracy of the survey. The results indicated that the nominal diameter error is approximately ±20% and the nominal albedo error is ±50%.
Paper III (Mueller et al. 2011) examined low delta-V NEOs and updated the error analysis presented in Paper I. The updated error analysis considers the various sources of uncertainty present in the ExploreNEOs observations: the measured flux uncertainty, the calibration uncertainty, the uncertainty in absolute magnitude (H), and the uncertainty of the Near-Earth Asteroid Thermal Model (NEATM) temperature parameter η. The first two uncertainty sources are observational errors from our Warm Spitzer measurements. The error in H magnitude is due to uncertainties and biases in ground-based surveys. η provides a first-order description of the thermal effects of surface roughness and thermal inertia, the latter of which is determined by regolith properties. In the framework of ExploreNEOs, η is not generally constrained by the data but is assumed based on an empirical correlation with the solar phase angle. A robust error margin is included in the Monte Carlo analysis developed by Mueller et al. (2011). The Monte Carlo procedure generates 1000 sets of synthetic fluxes distributed around the measured flux values. This Monte Carlo approach adopts the median value as the nominal albedo. These improved results are somewhat different than the values presented in Papers I and II. The Monte Carlo method also showed that an NEO's albedo error distribution is not well described by a Gaussian function, and Mueller et al. (2011) adopted asymmetric error bars to better capture the true uncertainty. For each NEO, Mueller et al. (2011) calculated the probability that the albedo falls within each of four bins (pV < 7.5%, 7.5% < pV < 15%, 15% < pV < 30%, and 30% < pV). These albedo bins were designed to correspond to taxonomic types and provide insight into potential mineralogy. We modified these bins in this work in order to classify E-, M-, and P-types from our X-complex sample.
There are 447 NEOs that have been observed and modeled in the ExploreNEOs program as of 2011 February 15. The albedo and diameter results for these objects have either been presented in one of the previous ExploreNEOs papers or will appear in the upcoming Paper VI (D. E. Trilling et al. 2011, in preparation). As stated above, our albedo results are subject to several sources of error, notably incorrect absolute magnitudes (H) and NEATM temperature parameters η. We are near completion of a ground-based photometry program that is targeting a large percentage of our Warm Spitzer sample in order to correct the H magnitudes (A. R. Hagen et al. 2011, in preparation). In the future, this will allow us to present more accurate individual albedos and average albedos. For the moment, we expect the errors on the albedos to be approximately ±50% (Harris et al. 2011). Despite the large errors, the large number of objects included for a given taxonomic class allows us to find the average with relatively high precision.
This work presents the nominal modeling results for all objects included, with a single exception. For the case of C-complex object (3671) Dionysus, we use a revised albedo value from Mueller et al. (2011). The inclusion of this revised value allows us to find a reasonable C-complex average despite the small C-complex sample size. We used the nominal ExploreNEOs albedo for (433) Eros even though it differs from the known value so that we preserve the statistical properties of our sample. The large discrepancy between the ExploreNEOs albedo and the known albedo is discussed in Paper I (Trilling et al. 2010). Briefly, it is due to the near pole-on observation of the object and the geometry's effect on the nominal H magnitude and η values.
2.2. Taxonomic Classes
We obtained taxonomic classifications for objects in our ExploreNEOs target list via two sources: previously published work and new classifications. The literature classifications include papers defining taxonomic systems as well as other large spectroscopic surveys. Our search was assisted by the Neese (2010) asteroid taxonomy catalog on the Planetary Data System. The complete list of sources is Tholen (1989), Xu et al. (1995), Binzel et al. (2001), Bus & Binzel (2002a), Binzel et al. (2004a), Binzel et al. (2004b), Stuart & Binzel (2004), Lazzarin et al. (2004), Lazzaro et al. (2004), and DeMeo et al. (2009). From these sources, we cataloged available classifications for each object within the Tholen (1984), Bus (Bus & Binzel 2002a), and Bus–DeMeo (DeMeo et al. 2009) systems. In total, we identified 86 published taxonomic classifications for objects with known ExploreNEOs albedos prior to 2011 February 15.
In addition to the previously published classifications, we classified 60 objects within the Bus–DeMeo system using a combination of publicly available spectra and new observations made by our group. All objects were classified using the online Bus–DeMeo taxonomic classifier13 described in DeMeo et al. (2009). Overlap exists between the objects classified in the literature and those classified for this work. A total of 118 ExploreNEOs objects have classifications presented in this work.
The publicly available spectra for objects within the ExploreNEOs sample are drawn from Reddy (2010) and the MIT-UH-IRTF Joint Campaign for NEO Spectral Reconnaissance.14 Our new observations come from an ongoing spectroscopy observing campaign to study ExploreNEOs targets. This observing campaign uses a variety of visible and near-infrared spectrographs and will be discussed in detail in C. A. Thomas et al. (2011, in preparation).
The Reddy (2010) and our current observing campaign data sets contain only near-infrared spectra from the SpeX instrument (Rayner et al. 2003) on NASA's Infrared Telescope Facility (IRTF). The Joint Campaign data include near-infrared SpeX data and visible spectra from SMASSI (Xu et al. 1995) or SMASSII (Bus & Binzel 2002b) when available. The spectra are classified using all available data, that is, including the visible wavelength data where present.
Table 1 presents the classifications and derived albedos for the 118 objects for which both taxonomic information and ExploreNEOs results were available. This table is divided by taxonomic complex. We use the definitions of the complexes defined in Binzel et al. (2004b) and used to calculate average complex albedos in Stuart & Binzel (2004). The list of types within the complexes is given in Table 2. One class is determined for each object for each available taxonomic system except in the case of the X-complex. Members of the X-complex can have two designations in the event that both a spectral classification (e.g., Xe, Xk) and an albedo-based classification (E, M, P) exist.
Table 1. Warm Spitzer Obtained Albedos Divided by Asteroid Taxonomic Class
| Number | Name | pv | σ+ | σ− | Tholen | Bus | Bus–DeMeo |
|---|---|---|---|---|---|---|---|
| C-complex | |||||||
| 2100 | Ra-Shalom | 0.14 | 0.10 | 0.06 | C (2) | Xc (5), C (7,8) | |
| 3671 | Dionysus | 0.69 | 0.33 | 0.25 | Cb (5,7,8) | ||
| 3671 | Dionysusa | 0.18 | 0.09 | 0.07 | Cb (5,7,8) | ||
| 65679 | 1989 UQ | 0.06 | 0.05 | 0.03 | B (5,6,7) | ||
| 99935 | 2002 AV4 | 0.23 | 0.19 | 0.11 | B (13) | ||
| 175706 | 1996 FG3 | 0.03 | 0.03 | 0.01 | C (4,5,6,7) | C* (13) | |
| Averageb | 0.23 | 0.15 | 0.13 | ||||
| Averagec | 0.13 | 0.06 | 0.05 | ||||
| S & B average | 0.101 | 0.027 | 0.027 | ||||
| D-complex | |||||||
| 17274 | 2000 LC16 | 0.02 | 0.02 | 0.01 | Xk (7) | D (1,11) | |
| 162998 | 2001 SK162 | 0.03 | 0.03 | 0.01 | T (6,7) | D (1) | |
| Average | 0.02 | 0.02 | 0.01 | ||||
| S & B average | 0.042 | 0.013 | 0.013 | ||||
| Q-complex | |||||||
| 1566 | Icarus | 0.14 | 0.10 | 0.06 | Q (8) | ||
| 1685 | Toro | 0.38 | 0.33 | 0.18 | S (2) | S (5,7,10) | Sq (11) |
| 1863 | Antinous | 0.11 | 0.08 | 0.05 | SU (2) | Sq (4,7) | |
| 2212 | Hephaistos | 0.06 | 0.08 | 0.03 | SG (2) | Sq (13) | |
| 2340 | Hathor | 0.60 | 0.28 | 0.21 | CSU (2) | Sq (5,7) | |
| 3122 | Florence | 0.21 | 0.20 | 0.10 | S (5,7) | Sqw (11) | |
| 4183 | Cuno | 0.10 | 0.10 | 0.05 | Sq (5,7) | ||
| 4544 | Xanthus | 0.37 | 0.23 | 0.16 | Q (13) | ||
| 5011 | Ptah | 0.11 | 0.11 | 0.05 | Q (13) | ||
| 5131 | 1990 BG | 0.96 | 0.38 | 0.39 | S (5,7) | Sq (13) | |
| 5143 | Heracles | 0.40 | 0.22 | 0.16 | V (3) | O (5,7) | Q (11,13) |
| 5626 | 1991 FE | 0.15 | 0.18 | 0.08 | S (5,7) | Sq (1) | |
| 5646 | 1990 TR | 0.66 | 0.42 | 0.29 | Q (1) | ||
| 6239 | Minos | 0.57 | 0.37 | 0.29 | Sqw (11) | ||
| 10115 | 1992 SK | 0.38 | 0.24 | 0.17 | S: (7) | Sq (13) | |
| 10563 | Izhdubar | 0.20 | 0.16 | 0.09 | Q (5,7) | ||
| 12711 | 1991 BB | 0.19 | 0.14 | 0.09 | Sr (5,7) | Q (1) | |
| 20826 | 2000 UV13 | 0.18 | 0.31 | 0.12 | Sq (7) | ||
| 21088 | 1992 BL2 | 0.26 | 0.32 | 0.14 | Q (1) | ||
| 22753 | 1998 WT | 0.27 | 0.17 | 0.11 | Sq (13) | ||
| 25916 | 2001 CP44 | 0.21 | 0.22 | 0.11 | Q (13) | ||
| 27346 | 2000 DN8 | 0.19 | 0.17 | 0.09 | Q (1) | ||
| 35107 | 1991 VH | 0.26 | 0.20 | 0.11 | Sk (5,7) | Sq (11,12,13) | |
| 40267 | 1999 GJ4 | 0.28 | 0.28 | 0.14 | Sq (4,7) | ||
| 66251 | 1999 GJ2 | 0.37 | 0.32 | 0.21 | Q (13) | ||
| 68216 | 2001 CV26 | 0.26 | 0.21 | 0.13 | Sq (1,12) | ||
| 68359 | 2001 OZ13 | 0.47 | 0.32 | 0.22 | Sq (13) | ||
| 85839 | 1998 YO4 | 0.17 | 0.16 | 0.08 | Q (1) | ||
| 85938 | 1999 DJ4 | 0.30 | 0.22 | 0.14 | Sq (4,7) | ||
| 86067 | 1999 RM28 | 0.17 | 0.16 | 0.09 | Q (1) | ||
| 137032 | 1998 UO1 | 0.13 | 0.11 | 0.06 | Sq (12,13) | ||
| 138883 | 2000 YL29 | 0.19 | 0.17 | 0.09 | Q (1) | ||
| 141052 | 2001 XR1 | 0.22 | 0.08 | 0.05 | Sq (7) | Sq (13) | |
| 143651 | 2003 QO104 | 0.14 | 0.12 | 0.07 | Q (13) | ||
| 159402 | 1999 AP10 | 0.35 | 0.24 | 0.16 | Sq (1,12) | ||
| 1997 UH9 | 0.36 | 0.23 | 0.15 | Sq (5,7,9) | |||
| 1997 US9 | 0.35 | 0.22 | 0.15 | Q (5,7) | |||
| 2002 NP1 | 0.26 | 0.19 | 0.12 | Q (1) | |||
| 2004 QT24 | 0.42 | 0.24 | 0.17 | Q (13) | |||
| 2007 RF5 | 0.21 | 0.18 | 0.09 | Sq (13) | |||
| Average | 0.29 | 0.05 | 0.04 | ||||
| S & B average | 0.247 | 0.060 | 0.060 | ||||
| S-complex | |||||||
| 433 | Erosd | 0.07 | 0.08 | 0.03 | S (2) | S (5,7,8) | S* (1,11) |
| 1627 | Ivar | 0.09 | 0.12 | 0.05 | S (2) | S (5,7,8) | S (1,13) |
| 1865 | Cerberus | 0.50 | 0.29 | 0.21 | S (2) | S (5,7) | S (13) |
| 1943 | Anteros | 0.17 | 0.15 | 0.08 | S (2) | L (4,6,7,10) | S* (1,11) |
| 1980 | Tezcatlipoca | 0.47 | 0.43 | 0.24 | SU (2) | Sl (5,7,8) | S*(11,12,13) |
| 2062 | Aten | 0.20 | 0.15 | 0.08 | S (2) | Sr (5,7) | |
| 4957 | Brucemurray | 0.18 | 0.19 | 0.09 | S (5,7) | ||
| 5587 | 1990 SB | 0.29 | 0.43 | 0.19 | Sq (5,7,8) | Sr (11) | |
| 6047 | 1991 TB1 | 0.80 | 0.44 | 0.35 | S (5,7) | S (11,13) | |
| 6455 | 1992 HE | 0.31 | 0.42 | 0.18 | S (5,7) | Srw (11) | |
| 7822 | 1991 CS | 0.28 | 0.18 | 0.12 | S (5,7) | S* (1) | |
| 7977 | 1977 QQ5 | 0.06 | 0.06 | 0.03 | S (5,7) | ||
| 10165 | 1995 BL2 | 0.68 | 0.45 | 0.27 | L (5,7) | ||
| 11066 | Sigurd | 0.38 | 0.31 | 0.18 | S (3) | K (7) | Sr (1) |
| 11398 | 1998 YP11 | 0.18 | 0.17 | 0.09 | Sr (7) | Sr (12,13) | |
| 12923 | Zephyr | 0.20 | 0.16 | 0.09 | S: (7) | ||
| 15745 | 1991 PM5 | 0.24 | 0.18 | 0.11 | S (7) | ||
| 16657 | 1993 UB | 0.09 | 0.09 | 0.04 | Sr (5,7) | ||
| 16834 | 1997 WU22 | 0.43 | 0.28 | 0.20 | S (4,7,8) | S* (1,13) | |
| 18882 | 1999 YN4 | 0.18 | 0.15 | 0.09 | S (4,7) | ||
| 20790 | 2000 SE45 | 0.10 | 0.11 | 0.05 | S (7) | S (11) | |
| 22099 | 2000 EX106 | 0.29 | 0.18 | 0.12 | S (6,7) | ||
| 25143 | Itokawa | 0.36 | 0.22 | 0.15 | S (6) | ||
| 36183 | 1999 TX16 | 0.44 | 0.39 | 0.23 | Ld (4,7) | ||
| 36284 | 2000 DM8 | 0.19 | 0.16 | 0.09 | Sq (7) | K (11) | |
| 54686 | 2001 DU8 | 0.37 | 0.32 | 0.20 | S (7) | ||
| 54690 | 2001 EB | 0.24 | 0.21 | 0.11 | Sl (7) | S (11) | |
| 55532 | 2001 WG2 | 0.14 | 0.12 | 0.06 | Sk (7) | ||
| 85709 | 1998 SG36 | 0.32 | 0.27 | 0.15 | Sr (13) | ||
| 85818 | 1998 XM4 | 0.30 | 0.23 | 0.15 | S (7) | ||
| 85989 | 1999 JD6 | 0.05 | 0.05 | 0.02 | K (4,7) | L (12) | |
| 86326 | 1999 WK13 | 0.27 | 0.21 | 0.12 | S (4,7) | ||
| 96590 | 1998 XB | 0.11 | 0.09 | 0.05 | S: (7) | ||
| 99907 | 1989 VA | 0.24 | 0.19 | 0.11 | Sq (5,7) | S* (11,13) | |
| 100926 | 1998 MQ | 0.37 | 0.22 | 0.16 | S (5,7) | ||
| 137064 | 1998 WP5 | 0.29 | 0.25 | 0.14 | Sl (4,7) | ||
| 161989 | Cacus | 0.29 | 0.21 | 0.13 | S (2) | ||
| 163001 | 2001 SE170 | 0.09 | 0.09 | 0.05 | Sr (13) | ||
| 1998 VO | 0.28 | 0.20 | 0.12 | S (6) | |||
| 1999 YG3 | 0.18 | 0.14 | 0.08 | S (4,7) | |||
| 2000 AD205 | 0.08 | 0.08 | 0.04 | K (13) | |||
| 2000 RS11 | 0.35 | 0.24 | 0.14 | Sa (9) | |||
| 2000 YF29 | 0.27 | 0.16 | 0.11 | S (6,7) | |||
| 2004 VC | 0.21 | 0.16 | 0.09 | Sr (13) | |||
| 2005 MC | 0.19 | 0.21 | 0.09 | Sr (1) | |||
| 2006 SZ217 | 0.16 | 0.14 | 0.07 | Sr (13) | |||
| Average | 0.26 | 0.04 | 0.03 | ||||
| S & B average | 0.239 | 0.044 | 0.044 | ||||
| V-complex | |||||||
| 3551 | Verenia | 0.28 | 0.21 | 0.14 | V (2) | V (8) | |
| 4055 | Magellan | 0.36 | 0.27 | 0.17 | V (2) | V (7,8,10) | V (11,13) |
| 5604 | 1992 FE | 0.71 | 0.32 | 0.23 | V (6,7,8) | V (11,13) | |
| 8566 | 1996 EN | 0.30 | 0.22 | 0.14 | V (1) | ||
| 52750 | 1998 KK17 | 0.46 | 0.25 | 0.20 | V (1,13) | ||
| 137052 | 1998 VO33 | 0.73 | 0.42 | 0.32 | V (5,7) | ||
| 137924 | 2000 BD19 | 0.11 | 0.09 | 0.05 | V (12) | ||
| Average | 0.42 | 0.13 | 0.11 | ||||
| S & B average | 0.417 | 0.147 | 0.147 | ||||
| X-complex | |||||||
| 3103 | Eger | 0.42 | 0.33 | 0.20 | Xe (5,7), E (9) | Xe (11) | |
| 3691 | Bede | 0.63 | 0.38 | 0.28 | Xc (5,7) | X* (13) | |
| 4660 | Nereus | 0.39 | 0.24 | 0.16 | Xe (6,7), E (8,9) | ||
| 5645 | 1990 SP | 0.06 | 0.08 | 0.04 | Xe (9) | ||
| 5751 | Zao | 0.53 | 0.35 | 0.23 | X (5,7,10), E (8) | ||
| 10302 | 1989 ML | 0.51 | 0.28 | 0.19 | X (4,6,7), E (14) | ||
| 17511 | 1992 QN | 0.72 | 0.31 | 0.25 | X (5,7) | ||
| 33342 | 1998 WT24 | 0.75 | 0.35 | 0.26 | Xe (9), E (15) | ||
| 85990 | 1999 JV6 | 0.07 | 0.06 | 0.04 | Xk (4,6,7) | ||
| 100085 | 1992 UY4 | 0.02 | 0.02 | 0.01 | P (16) | X* (12) | |
| 136564 | 1977 VA | 0.53 | 0.28 | 0.21 | XC (2,6) | X* (13) | |
| 137170 | 1999 HF1 | 0.10 | 0.09 | 0.05 | X: (7) | X* (13) | |
| 141079 | 2001 XS30 | 0.11 | 0.09 | 0.05 | Xc (7) | ||
| 152563 | 1992 BF | 0.08 | 0.08 | 0.04 | Xc (5,6,7) | ||
| 153219 | 2000 YM29 | 0.02 | 0.02 | 0.01 | X* (13) | ||
| 164202 | 2004 EW | 0.34 | 0.20 | 0.13 | X* (13) | ||
| 2000 CO101 | 0.17 | 0.12 | 0.08 | Xk (7) | |||
| 2001 UY4 | 0.03 | 0.02 | 0.01 | X (7) | |||
| Average | 0.31 | 0.08 | 0.07 | ||||
| S & B average | 0.072 | 0.025 | 0.025 | ||||
Notes. Each of the 118 objects included in this sample are displayed with the object's albedo, asymmetric error, and available taxonomic classifications in the Tholen, Bus, and Bus–DeMeo systems. For some objects the complex, but not the subclass, could be determined. These objects are noted as that complex followed by a star (e.g., C*). aAlternate albedo value of (3671) Dionysus from ExploreNEOs III (Mueller et al. 2011). bAverage C-complex albedo using the nominal albedo value for (3671) Dionysus. cAlternate average C-complex albedo using the alternate albedo value for (3671) Dionysus. dThis is the nominal ExploreNEOs albedo for Eros. The true albedo for this object is higher than presented here. For additional discussion please see Section 2.1. References. (1) ExploreNEOs concurrent spectral survey, C. A. Thomas et al. (2011, in preparation); (2) Tholen 1989; (3) Xu et al. 1995; (4) Binzel et al. 2001; (5) Bus & Binzel 2002a; (6) Binzel et al. 2004a; (7) Binzel et al. 2004b; (8) Stuart & Binzel 2004; (9) Lazzarin et al. 2004; (10) Lazzaro et al. 2004; (11) DeMeo et al. 2009; (12) Reddy 2010; (13) MIT-UH-IRTF Joint Campaign for NEO Spectral Reconnaissance; (14) Mueller et al. 2007; (15) Harris et al. 2007; (16) Volquardsen et al. 2007.
Table 2. Listing of Types Included in Each Taxonomic Complex
| Complex | Types Included |
|---|---|
| C | B, C, Cb, Cg, Ch, Cgh |
| D | D, T |
| Q | Q, Sq |
| S | S, Sa, Sk, Sl, Sr, K, L, Ld |
| V | V |
| X | X, Xc, Xk, Xe, E, M, P |
Download table as: ASCIITypeset image
For most objects, the online classification system returned a variety of possible subclasses. This is due primarily to our use of spectra containing only near-infrared wavelengths. The additional absorption features and slope information contained in the visible wavelength region are extremely beneficial to classification, especially when considering the relatively featureless C- and X-complexes. As described in DeMeo et al. (2009), the lack of visible wavelength data allows certain classes to occupy the same principal component space. This prevents the data from being formally classified via principal component analysis and all possible types are returned by the system. Some of these objects can still be classified if the presence or absence of weak absorption features typical to the potential subclasses are taken into account. These features are too small to be distinguished in principal component space and too small to affect the residuals between the input spectrum and the class average spectrum, but are indicative of certain classifications.
We examined the object's spectrum compared to the average spectra of the possible subclasses. Potential classifications were ruled out when the shapes, slopes, and/or residuals of the object in question were not consistent with the average subclass spectra. At times this examination allowed us to determine the precise subclass classification for the object. For some of our objects, we were unable to conclusively determine the subclass in the Bus–DeMeo system among the potential subclass assignments. Fortunately, our sample only required the complex of an object, not an accurate determination of the object's subclass. If the potential subclass classifications all belonged to a single complex, then the object was classified as belonging to that complex and the object was marked as the complex letter followed by a star (e.g., X*).
When an object has been assigned to several different subclasses within the same complex by different sources (either literature or new classification), this object is also marked with the complex letter and a star. This discrepancy has not changed the complex of any objects outside of the Sq- and S-classes. Although Sq is a subtype of S, it is considered part of the Q-complex (Binzel et al. 2004b). In the case where an object has different S-subtype classifications and one of them is Sq, we defer to the most recent data set. This rule applies unless the object was defined as Sq in the creation of the Bus–DeMeo taxonomic system (DeMeo et al. 2009). In that case, we defer to the initial DeMeo et al. (2009) taxonomic classification.
If the potential subclass classifications spanned more than one taxonomic complex, then the object was labeled as being of indeterminate complex and was removed from the sample. Four objects were removed because their spectra were indeterminate between the C- and X-complexes. The difficulty of determining subclasses and distinguishing between the C- and X-complexes is due to the ambiguity of making IR-only classifications. Since these classes have subtle visible wavelength spectral features, the visible wavelength component is often crucial to making definitive complex and subclass assignments for the relatively featureless classes.
3. RESULTS: AVERAGE ALBEDOS FOR TAXONOMIC CLASSES
We calculate the average albedos for the main taxonomic classes in near-Earth space. Table 1 shows the collection of albedo and taxonomy information for all objects in our sample, divided by complex. We also show the ExploreNEOs and Stuart & Binzel average albedos for the C-, D-, Q-, S-, V-, and X-complexes. We expect large errors on the albedo for each individual object in our sample (Harris et al. 2011). Given these large errors, we anticipate that the nominal albedo ranges for each class will be larger than those seen in the Stuart & Binzel sample. However, the mean errors within each complex should be, and are, small in general. The Stuart & Binzel (2004) average albedos are based on a sample of 36 objects divided among the complexes as follows: 6 C, 1 D, 1 O, 7 Q, 12 S, 3 V, and 6 X. We present here 118 objects divided among the complexes with the following distribution: 5 C, 2 D, 40 Q, 46 S, 7 V, and 18 X.
We use the asymmetric error bars introduced by Mueller et al. (2011) in order to better present the non-Gaussian distribution of uncertainty associated with the albedo calculation. In order to calculate the resulting asymmetric error on the average albedos, we consider the positive and negative errors separately. We take the separate positive and negative errors for each complex and propagate them using traditional propagation techniques ( , where N is the sample size). The final asymmetric error presented for a complex is the standard deviation of the mean folded in quadrature with the positive and negative propagated uncertainties. This method produces separate positive and negative uncertainties for the complex average albedo.
, where N is the sample size). The final asymmetric error presented for a complex is the standard deviation of the mean folded in quadrature with the positive and negative propagated uncertainties. This method produces separate positive and negative uncertainties for the complex average albedo.
The individual and average albedos for each complex are shown in Figures 1 and 2. Figure 1 shows individual albedos for each of the six complexes. The distribution of individual objects within a complex is compared to both the ExploreNEOs average (red diamonds) and the Stuart & Binzel (2004) average (blue squares). Figure 2 shows each individual albedo and its corresponding error for the C-, Q-, S-, and V-complexes. The horizontal ordering corresponds to the ordering in Table 1. The ExploreNEOs and Stuart & Binzel averages are also shown for these four complexes. The D-complex only has two objects and is therefore not displayed in this manner. The X-complex is displayed in Figure 3 with the horizontal ordering corresponding to the order in which the objects appear in Table 3.
Figure 1. Average albedos of NEAs by taxonomic type. Asteroids were divided into types using various publications and observational data from online resources and our complementary ground-based observing program (C. A. Thomas et al. 2011, in preparation). The black circles indicate individual Warm Spitzer albedos compared to our class averages (red diamonds) and previously published averages (blue squares). For the Q-, S-, and V-complexes, we show comparable averages with smaller errors than previous work by Stuart & Binzel (2004). The C-complex has one anomalous object, Dionysus (open circles), with an ambiguous albedo that produces two possible averages. Our D-complex average is based on only two objects. The average is consistent with the Stuart & Binzel average, which is based on the debiased population from a single D-complex observation. Our X-complex average samples the full albedo range of the class, but has less physical meaning than the other class averages due to the EMP degeneracy of the X-complex.
Download figure:
Standard image High-resolution imageFigure 2. ExploreNEOs albedo and error measurements for all objects in the Q-complex (top left), S-complex (top right), C-complex (bottom left), and V-complex (bottom right) as well as the ExploreNEOs (red diamonds) and Stuart & Binzel averages (blue squares). For each complex, the objects are arranged from left to right in the order in which they appear in Table 1. The spread along the x-axis is to separate each object for visual clarity. The C-complex shows both values for (3671) Dionysus (open circles) and the two resulting class averages. Despite the large individual errors, the sample sizes for the Q-, S-, and V-complexes allow us to calculate average albedos with greater precision than Stuart & Binzel.
Download figure:
Standard image High-resolution imageFigure 3. ExploreNEOs albedo and error measurements for all objects in the X-complex along with the ExploreNEOs (red diamond) and Stuart & Binzel (blue square) averages. The objects are ordered with increasing albedo and are in the same order as presented in Table 3. The objects are spread in the x-axis for visual clarity. Using the albedo value and the probability bin distribution, we are able to separate our X-complex sample into albedo-based classes where the E-types are high albedo (pV > 30%), M-types are of intermediate albedo (10% < pV < 30%), and P-types are low albedo (pV < 10%).
Download figure:
Standard image High-resolution imageTable 3. Determination of E-, M-, and P-types among the X-complex
| Number | Name | pv | σ+ | σ− | p1 | p2 | p3 | Type |
|---|---|---|---|---|---|---|---|---|
| 153219 | 2000 YM29 | 0.02 | 0.02 | 0.01 | 0.99 | 0.01 | 0.00 | P |
| 100085 | 1992 UY4 | 0.02 | 0.02 | 0.01 | 0.98 | 0.02 | 0.00 | P |
| 2001 UY4 | 0.03 | 0.02 | 0.01 | 0.98 | 0.02 | 0.00 | P | |
| 5645 | 1990 SP | 0.06 | 0.08 | 0.04 | 0.71 | 0.26 | 0.03 | P |
| 85990 | 1999 JV6 | 0.07 | 0.06 | 0.04 | 0.67 | 0.31 | 0.02 | P |
| 152563 | 1992 BF | 0.08 | 0.08 | 0.04 | 0.61 | 0.36 | 0.03 | P, poss M |
| 137170 | 1999 HF1 | 0.10 | 0.09 | 0.05 | 0.49 | 0.48 | 0.03 | Either P or M |
| 141079 | 2001 XS30 | 0.11 | 0.09 | 0.05 | 0.44 | 0.52 | 0.04 | M, poss P |
| 2000 CO101 | 0.17 | 0.12 | 0.08 | 0.17 | 0.68 | 0.15 | M | |
| 164202 | 2004 EW | 0.34 | 0.20 | 0.13 | 0.01 | 0.38 | 0.61 | E, poss M |
| 4660 | Nereus | 0.39 | 0.24 | 0.16 | 0.01 | 0.30 | 0.69 | E |
| 3103 | Eger | 0.42 | 0.33 | 0.20 | 0.02 | 0.29 | 0.69 | E |
| 10302 | 1989 ML | 0.51 | 0.28 | 0.19 | 0.00 | 0.14 | 0.86 | E |
| 136564 | 1977 VA | 0.53 | 0.28 | 0.21 | 0.00 | 0.13 | 0.87 | E |
| 5751 | Zao | 0.53 | 0.35 | 0.23 | 0.00 | 0.16 | 0.84 | E |
| 3691 | Bede | 0.63 | 0.38 | 0.28 | 0.00 | 0.10 | 0.90 | E |
| 17511 | 1992 QN | 0.72 | 0.31 | 0.25 | 0.00 | 0.03 | 0.97 | E |
| 33342 | 1998 WT24 | 0.75 | 0.35 | 0.26 | 0.00 | 0.02 | 0.98 | E |
Notes. The 18 X-complex objects are shown with their albedo, asymmetric error, and probabilities of falling into one of the three defined albedo ranges (p1: pV < 10%, p2: 10% < pV < 30%, and p3: 30% < pV).
Download table as: ASCIITypeset image
C-Complex. There are five objects in our sample that have been classified as C-complex asteroids. Four of these objects have albedos within the range expected for the C-complex. The fifth object is (3671) Dionysus, whose nominal albedo of 0.689 is much higher than expected for a C-complex asteroid. Dionysus was examined in Mueller et al. (2011) because of this class-albedo discrepancy. That paper concludes that this disagreement was due to the assumed η (beaming parameter) value in the ExploreNEOs thermal modeling (which is derived from an empirical linear relationship between η and solar phase angle—see ExploreNEOs I and II) being inappropriate in this case. A corrected calculation yields an albedo of 0.178, which is more consistent with the Cb classification. Ideally, any given spectral class would have enough objects with albedos to make a single incorrect datum inconsequential. However, given the small number of objects in this spectral class presented here, this single point has a large effect on the class average. For this reason, we present two class averages for the C-complex: one with the original Dionysus value (mean = 0.23+0.15−0.13) and one with the corrected Mueller et al. Dionysus value (mean = 0.13+0.06−0.05). The initial and corrected albedo for Dionysus and the two averages that result all appear in Figures 1 and 2. The average C-complex albedo using the corrected Dionysus albedo is consistent with the Stuart & Binzel (2004) complex average.
D-Complex. There are currently only two objects in our sample that have been classified as D-complex asteroids. Due to the small number of objects, we do not intend the average calculated here to serve as a final D-complex class average. Our preliminary D-complex average albedo is 0.02+0.02−0.01. We show the results for the D-complex to highlight the precision with which ExploreNEOs can determine individual albedos for low albedo objects. Due to this precision, we will not require as many albedos for the D-complex to get an accurate average albedo as compared to the brighter spectral classes. This is fortunate because D-class objects are not as common in near-Earth space as Q- and S-class objects. We anticipate identifying a small number of additional D-complex objects within our sample through our ongoing ground-based observing campaign.
Q-Complex. There are 40 objects in our sample that have been classified as Q-complex. The objects span the range of expected Q-complex albedos but there are also possible outliers on the low and high albedo ends. Because of the large sample size, we can readily calculate the average albedo for this complex. Our derived average albedo of 0.29+0.05−0.04 is consistent with and slightly higher than the Stuart & Binzel (2004) value of 0.247 ± 0.060. The Q-complex contains both Q- and Sq-class objects. We are unable to distinguish the average albedos of these two classes from the complex average.
S-Complex. There are 46 objects in our sample that have been classified as S-complex. As expected, the S-complex objects have a distribution very similar to the Q-complex, but with a slight shift to lower albedo. Our derived average albedo of 0.26+0.04−0.03 is again consistent with and slightly higher than the Stuart & Binzel (2004) value of 0.239 ± 0.044.
The S-complex contains all S-types (except the Sq-type), as well as the K- and L-types. Since the K- and L-objects are expected to have different compositions from the S-types, we also calculate the average albedo of objects solely within the S-types. This derived average albedo is 0.26+0.04−0.02. The inclusion of K- and L-objects does not change the derived average albedo. Since our sample includes only two K- and three L-type objects, we cannot calculate reliable class averages for these classes at this time.
V-Complex. There are seven objects in our sample that have been classified as V-complex. These objects span the nominal expected range for V-complex asteroids and also show potential high and low albedo outliers. Despite the small number of objects within this population we were able to constrain the V-complex average albedo to slightly greater precision than the Stuart & Binzel average. Our V-complex average albedo of 0.42+0.13−0.11 is virtually indistinguishable from the Stuart & Binzel average of 0.417 ± 0.147.
X-Complex. There are 18 objects in our sample that have been classified as X-complex. The X-complex is a group of objects based on spectral properties that encompasses three types that are only distinguishable when the albedo is known. When geometric albedos are known for these X-type bodies they can be separated into the E-, M-, and P-classes (Bowell & Lumme 1979; Tholen 1984), where the E-types are high albedo (pV > 30%), M-types are of intermediate albedo (10% < pV < 30%), and P-types are low albedo (pV < 10%) objects (Clark et al. 2004).
The 18 objects in our sample span the large range of albedos expected from the X-complex. The combination of spectral classification and albedo allow us to identify E-, M-, and P-type membership within our sample. Table 3 shows the X-complex objects with albedos and corresponding errors along with the probability bin values. Mueller et al. (2011) introduced probability bins as an alternate method of displaying the error of an albedo value by showing the likelihood that the true albedo would belong to one of the four bins. In order to classify our X-complex sample into the albedo-based E-, M-, and P-classes the albedo bins used here have been defined to match the E-, M-, and P-class albedo boundaries (i.e., three bins defined as p1: pV < 10%, p2: 10% < pV < 30%, and p3: 30% < pV). This allows for a more straightforward measure of the statistical likelihood of an object being E-, M-, or P-type. Objects are assigned to a class if all of the following conditions are met: (1) the object's nominal albedo falls within the albedo range for that class, (2) the corresponding probability bin displays a probability greater than 50% that the object's albedo falls within the albedo range for the class, and (3) the greatest probability bin value is at least twice as probable as the next largest bin value. Four objects do not meet all three of these conditions and therefore cannot be conclusively classified. Three of these four objects meet the first two conditions and are noted with their most probable albedo-based classification as well as the other potential class assignment. The albedo of the fourth object, (137170) 1999 HF1, is extremely close to the boundary between the P- and M-types and the corresponding probability bins show nearly equal probability of the object belonging to either class. For this reason, we cannot distinguish between a P- or M-type classification for this object, however, an E-type classification can be ruled out. (3103) Eger, (4660) Nereus, (5751) Zao, (10302) 1989 ML, and (33342) 1998 WT24 have previously been classified as E-type objects (Stuart & Binzel 2004; Lazzarin et al. 2004; Mueller et al. 2007; Harris et al. 2007). (100085) 1992 UY4 has previously been classified as P-type (Volquardsen et al. 2007). Our current class assignments agree with these previous classifications. One object of interest in this sample is (152563) 1992 BF, which as been identified as having an orbit solution dependent on the Yarkovsky force (Vokrouhlický et al. 2008).
The distribution of albedos and errors for the individual X-complex objects are shown in Figure 3 along with the ExploreNEOs and Stuart & Binzel class averages. The objects are placed in order of increasing albedo in this figure in order to display the distinction between the low and intermediate (P- and M-types) albedo objects and the high albedo (E-type) objects. Our X-complex average albedo of 0.31+0.08−0.07 is much larger than the value of 0.072 ± 0.025 presented by Stuart & Binzel. In this instance the results of the population debiasing present in the Stuart & Binzel sample are evident. The low albedos of the P-type objects apparently dominate the debiased X-complex population.
Our X-complex average likely reflects the variety of the population, but our average has no real physical meaning because of the EMP degeneracy. This degeneracy makes it difficult to assign an albedo to an X-complex object for calculations of an individual object's physical properties. The verified spread in albedos throughout the population (pV = 0.023–0.55 in Stuart & Binzel, pV = 0.02–0.75 in this work) would cause large uncertainty in any individual diameter calculation derived from an X-complex average. However, a debiased X-complex average would inform our understanding of the X-complex component of the NEO population. Such an average could be used in the conversion from H magnitudes to size frequency distributions and in establishing the number and H magnitude of D > 140 m potential Earth impactors. In the future we can calculate the averages for the individual E, M, and P populations, which can be used for size frequency distributions in combination with E, M, and P abundances within the X-complex in near-Earth space. However, E-, M-, and P-class averages would not be as broadly useful for examining the physical properties of individual objects since the albedo of the object would have to be known in order to use the appropriate class average.
4. DISCUSSION
4.1. Fractional Abundances
In addition to average class albedos, Stuart & Binzel (2004) also present the debiased fractional abundances of taxonomic classes within the NEO population. For the classes examined here these fractions are C = 10%, D = 17%, Q = 14%, S = 22%, V = 1%, and X = 34%. This work presents the albedo and taxonomic class for 118 objects. Our sample has the following fractional distribution: C = 4%, D = 2%, Q = 34%, S = 39%, V = 6%, and X = 15%. This comparison allows us to comment on the biases within our sample. We target only known NEOs, so most of the sample bias originates from the discovery statistics. NEO searches are optical magnitude limited and the magnitude of a given object depends on its size and albedo. For large sizes, objects of all albedos should be well sampled, and are (Trilling et al. 2010). However, for small objects only those with higher albedos, and therefore brighter apparent magnitudes than their low albedo counterparts, will be well sampled by the discovery surveys, as seen in Paper I (Trilling et al. 2010). As a result, discovery statistics present a bias against small, low albedo objects. The discovery bias explains why our sample underrepresents the darker C- and D-complexes and overrepresents the brighter Q-, S-, and V-complexes. The underrepresentation of the X-complex is likely due to underrepresentation of the low-albedo P-type component. This underrepresentation of the P-type component can also be seen in the high average X-complex albedo compared to the debiased X-complex Stuart & Binzel average. In addition to this discovery bias, the spectroscopy sample provides a slight bias against the C- and X-complex objects because of the ambiguity in distinguishing between these classes for some objects. As discussed in Section 2.2, four objects were removed from the sample because their taxonomic complex could not be determined. Obtaining visible spectroscopy data for objects within our Warm Spitzer sample has become a critical part of our observing campaign. These visible wavelength observations will allow us to definitively classify these currently ambiguous objects and will provide additional insight into the mineralogy of a wide variety of objects.
To further investigate observational bias we examine the fractional abundances for objects with diameters smaller than and larger than 1 km. Most classes agree with the total population fractional abundance values to within a couple percent. However, larger variations are found when examining the X-complex. For bodies smaller than 1 km, the X-complex comprises 22% of the 46 object population, while for bodies larger than 1 km, it comprises 11% of the 72 object population. These differing values are due to bright E-class objects comprising the majority of the D < 1 km X-complex population. The majority of E-class objects in our sample have diameters smaller than 1 km and their absence in the D > 1 km sample likely contributes to the lower X-complex fractional abundance value.
4.2. Space Weathering
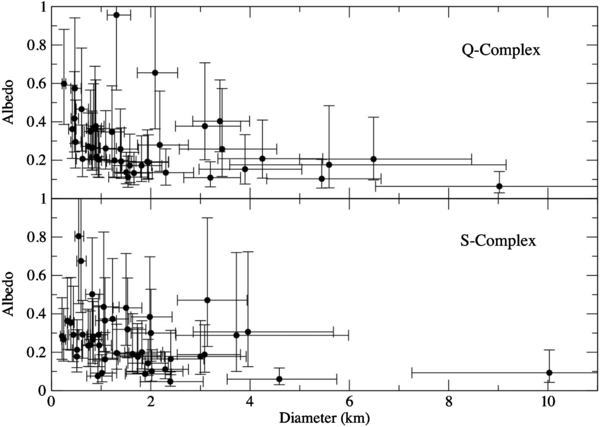
Collisional evolution theories for small bodies indicate that the expected lifetime of a body varies with the asteroid size (O'Brien & Greenberg 2005). Since a large object will have a longer collisional lifetime than a smaller body, large objects will have a greater age, on average, than small objects. This concept is particularly important for our understanding of S- and Q-type spectral and albedo variations. Exposure to space allows a process known as space weathering to increase the spectral slope, decrease the band depth, and lower the albedo of a silicate object such as the S- and Q-type asteroids (Adams & McCord 1971; Pieters et al. 2000). The space weathering effect increases with time until a point when saturation is reached (Noble et al. 2001). In addition to surfaces refreshed via catastrophic collisions, smaller collisions and YORP spin-up of small bodies covered in regolith can cause movement (and possibly removal) of the regolith, which would reset the surface age (Richardson et al. 2005; Fahnestock & Scheeres 2009; Delbo et al. 2011). Therefore smaller objects should not be as space weathered and would be expected to have higher albedos in general than their larger, older counterparts. For both the S- and Q-complexes we see a trend of higher albedo with smaller object diameter (Figure 4). This is expected since small asteroids should, on average, have younger, fresher surfaces. This trend was previously seen in the NEA population by Delbó et al. (2003) and is expected given our current understanding of the space weathering process on S- and Q-type bodies. The albedo–diameter trend is also present in the overall sample (Trilling et al. 2010). The trend could be due to the S- and Q-types numerically dominating the sample or it could be evidence of this space weathering trend throughout the population. The other complexes do not have enough objects to comment on the relationship between albedo and diameter within their populations.
Figure 4. Diameter vs. albedo for Q- and S-complex objects. The data show a trend of higher albedo with smaller object diameter for both the Q- and S-complexes. This trend was previously seen in the NEA population by Delbó et al. (2003).
Download figure:
Standard image High-resolution imageOur average albedos for the S- and Q-complexes are equivalent to the Stuart & Binzel (2004) values within errors, though our values are slightly higher. Since the difference between our averages and those of Stuart & Binzel (2004) are comparable to the difference between S- and Q-complex average albedos, the differences between our results and those of Stuart & Binzel (2004) could be the result of probing smaller sizes. However, the Stuart & Binzel averages are the result of a debiased complex population such that the resulting average should well sample the population of the smallest (and therefore highest albedo) objects within those classes. We can compare the size ranges examined by Stuart & Binzel and this work. Stuart & Binzel (2004) have 12 S-complex asteroids with sizes from 0.16 to 9.12 km (if you exclude Eros) and 7 Q-complex asteroids with sizes from 0.29 to 3.57 km (Harris 1998; Harris et al. 1998; Harris & Davies 1999; Harris & Lagerros 2002; Delbó et al. 2003). Our sample contains 46 S-complex asteroids from 0.21 to 10.01 km (if we exclude Eros) and 40 Q-complex asteroids from 0.25 to 9.02 km. The lower size limits of our sample are quite similar to that of Stuart & Binzel. Therefore, while the possible higher average albedos in our sample are not the direct result of sampling smaller sizes, they could be due to our S- and Q-complex samples containing more small-diameter, high-albedo objects than those of Stuart & Binzel (2004).
4.3. Comparisons to Previous Results
Ryan & Woodward (2010) calculated revised IRAS Main Belt albedos using the NEATM (Harris 1998). We can compare our taxonomic averages and population average with those calculated for the Main Belt (Table 4). Due to the extremely low number of known Q-types in the Main Belt, no average Q-complex albedo exists for the Main Belt. The C-, S-, V-, and X-complexes show higher average albedos in the near-Earth population. This is consistent with the conclusions of previous work. Stuart & Binzel (2004) showed higher NEO albedos for the C- and S-complexes, while Delbó (2004) also showed evidence of higher NEO albedos throughout the NEO population. The D-complex shows a near-Earth albedo average less than that seen in the Main Belt. This could be due to the small number of objects included in our D-complex average calculation. Acquiring additional D-complex albedos will show if this darkening of D-complex objects in the near-Earth population is real. Our overall NEA population average albedo of 0.28 is much larger than that found in the Main Belt (0.11 traditionally, 0.08 in Ryan & Woodward 2010). Delbó et al. (2003) showed a similar average NEO albedo of 0.25. However, both of these samples are biased. Stuart & Binzel (2004) calculated a debiased NEO average albedo of 0.14 ± 0.02 and Morbidelli et al. (2002) found that a 1 km NEO corresponded to H = 17.85 for a debiased population, which implies an average albedo of 0.13. Both of these debiased NEO average albedos are larger than the Main Belt averages.
Table 4. Comparison of Main Belt Average Albedos from Ryan & Woodward (2010) with Warm Spitzer Derived Averages
| Taxonomic Complex | Main Belt | Near-Earth |
|---|---|---|
| C | 0.066 | 0.13 |
| D | 0.067 | 0.02 |
| Q | ... | 0.29 |
| S | 0.155 | 0.26 |
| V | 0.348 | 0.42 |
| X | 0.113 | 0.31 |
| Total population | 0.081 | 0.28 |
Download table as: ASCIITypeset image
There are several potential reasons for the differences in albedos between the NEO and Main Belt populations. The discrepancy could be due to the different size regimes examined for each sample. The Main Belt albedos (Tedesco et al. 2002; Ryan & Woodward 2010) are from the IRAS catalog which primarily sampled objects with diameters larger than 10 km. In contrast, our albedo sample has only two objects, (433) Eros and (1627) Ivar, with diameters larger than 10 km. Additionally, we do not expect the space weathering rate to be the same in both the near-Earth and Main Belt populations since the rate of weathering depends on the distance from the sun (Nesvorný et al. 2010). We expect smaller objects to be statistically younger and therefore fresher, although the collisional rates are higher in the Main Belt population than they are in near-Earth space. For similarly sized objects we expect fresher objects in the Main Belt. However, the large difference in sizes between the NEO and Main Belt objects could exceed the space weathering and collisional contributions and display fresher surfaces within the ExploreNEOs sample than within the IRAS sample. The discrepancy could also be due to the NEO population being an incomplete sample of the Main Belt population. The inner Main Belt is the largest contributor to the NEO population (Bottke et al. 2002) and contains the brighter objects in the Main Belt (Gradie & Tedesco 1982). Knowing this, we expect the NEO population average albedo to be brighter than the average albedo of the Main Belt. It is possible that this source region bias also affects the individual taxonomic complexes, which contain within them varieties of compositions and surface properties that effect the albedo. Our brighter NEO complex averages might be explained if the NEO taxonomic complexes only represent the brighter fraction of the corresponding Main Belt complex population. Additionally, the difference between NEO and Main Belt albedos may be due to heating effects within the NEO population. For example, certain carbonaceous chondrites will initially darken when exposed to heat, but will start to get brighter when heated past 500°C (T. Hiroi 2011, private communication). This heating effect is unlikely to be a large contributor to the difference in albedos between NEOs and MBAs. The likely explanation of this difference in albedos is a combination of these and other factors.
We can also compare our average albedos with laboratory measurements of meteorites. Piironen et al. (1998) determined the single particle albedos of ordinary chondrites and C2 carbonaceous chondrites to be 0.50 ± 0.25 and 0.15 ± 0.02, respectively. Use of the Lumme–Bowell scattering model (Lumme & Bowell 1981) with these values yields geometric albedos of 0.13–0.24 for ordinary chondrites and 0.04–0.07 for carbonaceous chondrites. The Q-complex provides the best spectral match to ordinary chondrites and some S-complex objects are thought to be space weathered objects of ordinary chondritic, Q-complex origin. The albedos for ordinary chondrites are lower than the average albedos of the Q- and S-complexes, but are within the range of albedos seen in our Q- and S-complex samples. This suggests that some objects within those complexes are consistent with ordinary chondrites. The ordinary chondrite albedo range is in agreement with the Main Belt S-complex average. The carbonaceous chondrites are spectrally similar to the C-complex asteroids. The albedo for carbonaceous chondrites is lower than our C-complex albedo, but is within the range of albedos seen for the complex. The carbonaceous chondrite albedos are in agreement with the Main Belt C-complex average. The fact that measured MBA albedos provide a better match to meteorite albedos than NEA albedos is strange given our current understanding of meteorite delivery from the Main Belt to near-Earth space before landing on Earth.
Two of our X-complex objects have been observed by radar15: (3013) Eger and (17511) 1992 QN. Both of these objects were classified as E-type using our Warm Spitzer albedos and albedo probability bins. Eger was also previously classified as E-type by Gaffey et al. (1992). Benner et al. (2008) showed that E-type NEAs have very high circular polarization ratios (average = 0.892) while the M- and P-types have much lower values (averages = 0.143 and 0.188, respectively). The SC/OC ratios for Eger and 1992 QN rank among the highest of 214 NEAs detected by radar that were reported by Benner et al. (2008) with SC/OC ratios of 0.92 ± 0.06 and 1.10 ± 0.19, respectively (Benner et al. 1997, 2008). The measured high radar circular polarization ratios of Eger and 1992 QN are consistent with our classifications as E-type objects. In return, our classification of 1992 QN as an E-type object provides independent support for the apparent link between E-type classification and large radar SC/OC.
5. CONCLUSIONS AND FUTURE WORK
We have combined Spitzer-derived albedos with spectroscopically determined taxonomic types for 118 NEOs. We find average albedo values of 0.29+0.05−0.04, 0.26+0.04−0.03, and 0.42+0.13−0.11 for the Q-, S-, and V-complexes, respectively. We also report preliminary average albedo estimates of 0.13+0.06−0.05, 0.02+0.02−0.01, and 0.31+0.08−0.07 for the C-, D-, and X-complexes, respectively. Our results agree with the previous work of Stuart & Binzel (2004), with the exception of the X-complex. However, the disagreement over the X-complex average is due to the fact that the Stuart & Binzel sample was a debiased average, while no debiasing appears in our sample. Therefore, our values are measuring two different populations and are not contradictory. The close agreement of our C-, Q-, S-, and V-complex average albedos with the debiased Stuart & Binzel average albedos shows that debiasing does not have a significant effect on calculations for these classes. We use ExploreNEOs albedo values to identify E-, M-, and P-type objects within the X-complex sample.
A crucial component of our observing campaign is the acquisition of accurate H magnitudes for a large fraction of the ExploreNEOs sample. The inclusion of improved H magnitudes will result in increased precision and accuracy in the individual albedos and average albedos. This increased precision and accuracy will allow us to study the true range of albedos for each class. We will continue to collect albedo values from our ExploreNEOs observations and to study the spectral properties of the Warm Spitzer sample through our visible and near-infrared spectroscopy observations. These observations will increase the sample size available for each taxonomic complex. We will be able to improve our calculated average albedos for all the complexes examined. In particular, we seek to improve the averages available for the C-, D-, and X-complexes and add additional complexes to our calculations, such as the A-, O-, and R-complexes. The increased sample size will also allow us to study differences in average albedos for the types that comprise the complexes (e.g., Sq- and Q-types; K- and L-types in the S-complex). These types often have different surface properties or compositions. Our growing sample will allow us to study additional details of the albedo differences by type that have not been previously investigated.
This work is based in part on observations made with the Spitzer Space Telescope, which is operated by JPL/Caltech under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech.
Some of this work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration (NASA). This material is based in part upon work supported by NASA under the Science Mission Directorate Research and Analysis Programs.
Part of the data utilized in this publication were obtained and made available by the MIT-UH-IRTF Joint Campaign for NEO Reconnaissance. The IRTF is operated by the University of Hawaii under Cooperative Agreement no. NCC 5-538 with the National Aeronautics and Space Administration, Office of Space Science, Planetary Astronomy Program. The MIT component of this work is supported by the National Science Foundation under Grant 0506716.
Facilities: Spitzer (IRAC) - Spitzer Space Telescope satellite, IRTF (SpeX) - Infrared Telescope Facility
Footnotes
- 12
- 13
- 14
- 15