Temporal evolution of electron density and temperature in low pressure transient Ar/N₂ plasmas estimated by optical emission spectroscopy

The experimental set-up used in this work was described in detail before [4], hence only the most important parameters shall be repeated here. The DBD-Jet was made from a small glass tube with an inner diameter of 4 mm which served as plasma vessel and extended into a cone shape at the gas inlet. Plasma was ignited by applying a sine-wave high-voltage with a frequency of 30 kHz between two electrodes made from aluminium-tape. From the discharge tube the plasma flow expanded into a larger glass tube which was evacuated by a turbomolecular pump and served as an expansion volume. To systematically study the impact of gas composition on the plasma parameters, the original set-up was modified by an additional mass flow controller which allowed to add small admixtures of nitrogen to the argon gas. For all presented experiments the argon flow was kept constant at 100 sccm while the nitrogen flow was varied between 0% and 4%. The pressure inside the discharge tube was estimated by laser absorption measurements similar as in [4] to be 155 Pa (1.13 torr). To provide optical access for the laser in axial direction, a small hole was located in the back electrode of the discharge tube.

Emission spectra were taken by a Czerny–Turner monochromator with an attached intensified-CCD camera (Princeton Instruments PI-MAX4 1024f). All spectra were acquired radially in the discharge tube similar to the previous experiments. Data was acquired for 90 frames, equally distributed over the discharge cycle. For each frame the exposure time was 500 ns. A relative response calibration was performed for the set-up using a Ocean Optics HL2000 Tungsten Halogen lamp prior to measurement. Similar to previous observations in [4], light intensity was found to vary by orders of magnitude within the discharge cycle (see figure 4).

Addition of nitrogen to the driving gas gave rise to optical emission from the intensive first positive system (1PS) of N₂ (see figure 1). Due to the long lifetime of the radiating molecular states (few μs) [6], emission intensities of nitrogen exhibited smaller variations during the discharge cycle than argon emissions used for plasma diagnostics. As a result, N₂ emissions were found to disturb peak fitting of the argon emissions especially during the phases of reduced intensity.

Zoom In Zoom Out Reset image size

To enhance data quality, nitrogen emission of the 1PS originating from ${{\rm{B}}}^{3}{{\rm{\Pi }}}_{{\rm{g}}}({{\rm{v}}}^{{\prime} })\to {{\rm{A}}}^{3}{{\rm{\Sigma }}}_{{\rm{u}}}({{\rm{v}}}^{{\prime\prime} })$ transitions was modelled in the respective wavelength range and subtracted from the emission spectra. For spectra simulation, all molecular energy levels up to a rotational quantum number J = 60 and their possible optical transitions were created according to [7]. Molecular bands were generated by superposition of all created transitions assuming Gaussian line shapes for each individual line. Individual line intensities within a band were calculated from ${{\rm{B}}}^{3}{{\rm{\Pi }}}_{{\rm{g}}}({{\rm{v}}}^{{\prime} })$ level population assuming a Maxwell–Boltzmann distribution among the rotational levels. Transition strengths were calculated from the corresponding Franck–Condon and Hoenl-London factors. The rotational temperature T_rot was used as free parameter allowing the fit to adjust the band shape to the observed spectrum. Due to the long lifetime of ${{\rm{B}}}^{3}{{\rm{\Pi }}}_{{\rm{g}}}({{\rm{v}}}^{{\prime} }),{T}_{{\rm{rot}}}$ was assumed to be a good indicator for the argon gas temperature T_gas which was required for analysis of argon emission lines [6]. Intensities of each band were free fit parameters since they were not required for further analysis in this work. Energies for all ${{\rm{B}}}^{3}{{\rm{\Pi }}}_{{\rm{g}}}({{\rm{v}}}^{{\prime} })$ and ${{\rm{A}}}^{3}{{\rm{\Sigma }}}_{{\rm{u}}}({{\rm{v}}}^{{\prime\prime} })$ states were calculated according to energy formulas provided in [7] using constants provided in [8, 9]. Levels of ${{\rm{A}}}^{3}{{\rm{\Sigma }}}_{{\rm{u}}}({{\rm{v}}}^{{\prime\prime} })$ were of Hunds coupling type a while for ${{\rm{B}}}^{3}{{\rm{\Pi }}}_{{\rm{g}}}({{\rm{v}}}^{{\prime} })$ a transition from coupling type a to type b for levels with j > 30 was assumed. Franck–Condon Factors were taken from [10] and Hoenl-London factors were calculated according to [11].

Emission intensities of the prominent argon $2{\rm{p}}\to 1{\rm{s}}$ transition array were subsequently estimated for each recorded frame from the area of their corresponding peaks considering the modelled nitrogen background emission.

The previously presented method for estimation of T_e will only be discussed briefly in this work and for a detailed description the reader is referred to [4]. The model combined direct estimation of the 1s states by an established self-absorption technique with CRM of the relative argon Paschen 2p state densities [5]. The underlying CRM was based on a model by Zhu and Pu which was extended by individually resolving higher-energetic levels. For a detailed description of the processes incorporated by the model see [4, 12]. In this work, the cross sections for excitation transfer for $1{{\rm{s}}}_{5}\leftrightarrow 1{{\rm{s}}}_{4},1{{\rm{s}}}_{4}\leftrightarrow 1{{\rm{s}}}_{2}$ and $1{{\rm{s}}}_{3}\leftrightarrow 1{{\rm{s}}}_{2}$ were rescaled to match with notably higher experimental rate coefficients reported in [13].

While a total of 31 excited argon levels was considered for modelling, only optical emission from the argon Paschen $2{\rm{p}}\to 1{\rm{s}}$ transition array, which is commonly found to be the most intensive for low-pressure argon discharges, was used for data analysis in the presented work. In each recorded frame, densities of all four 1s levels were estimated from their radiation trapping. The same line pairs and absorption length as in [4] were used for the self-absorption technique and with the densities of the 1s states known, relative densities of the 2p states became available from the emission intensities according to equation (1)

$$\begin{eqnarray}&&{I}_{2{\rm{p}}\to 1{\rm{s}}}\sim {n}_{2{\rm{p}}}{A}_{2{\rm{p}}\to 1{\rm{s}}}\gamma ({n}_{1{\rm{s}}},{T}_{1{\rm{s}}},l).\end{eqnarray} \tag{ 1 }$$

Here ${n}_{2{\rm{p}}},{n}_{1{\rm{s}}},{A}_{2{\rm{p}}\to 1{\rm{s}}},\gamma ,{T}_{1{\rm{s}}}$ and l denote number densities of the upper and lower level of the transition, the transitions Einstein coefficient for spontaneous emission (taken from [14]), the light escape factor, the temperature of the absorbing 1s levels as well as the optical absorption length.

The electron temperature was estimated by comparing observed relative densities of several 2p states with results of the CRM for a range of electron temperatures. In this work a Maxwell–Boltzmann distribution was assumed for the EEDF to demonstrate the method. For a discussion on the impact of non-maxwellian EEDFs see [4].

In each frame the particular 1s densities, estimated from self absorption, were fed to the CRM to calculate excitation rates and radiation trapping. From the best match between measurement and simulation, T_e was estimated for each 2p level individually.

By measuring 1s state densities directly instead of solving the corresponding rate-balance equations (RBEs) their densities were kept constant within the solving process of the CRM. Therefore, they were no longer affected by its input parameters (in particular n_e). Hence the dominating population processes of the 2p states scaled linear with ${{n}}_{{e}}$ and population ratios lost their sensitivity to variations of electron density.

However, population dynamics of the four 1s states in the collisional phase of the discharge were governed by electron impact processes. Therefore their measured absolute number densities depended directly on n_e. Although 1s number densities themselves reacted only slowly on changes of plasma parameters and hence were not suited for a time-resolved estimation of n_e, the rate of the density variation was utilized for a quantitative analysis. The underlying idea is to compare observed changing rates between subsequent frames at t and t − τ with simulated changing rates from the CRM. Based on their measured density profiles the changing rate R(t) for each 1s state can be described as

$$\begin{eqnarray}&&{R}_{{\rm{mea}}}(t)=\displaystyle \frac{{{\rm{d}}{n}}_{1{\rm{s}}}}{{\rm{d}}{t}}\approx \displaystyle \frac{{n}_{1{\rm{s}}}(t)-{n}_{1{\rm{s}}}(t-\tau )}{\tau }.\end{eqnarray} \tag{ 2 }$$

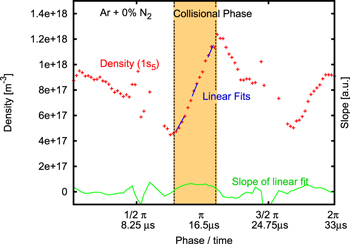
While generally a direct estimation of the rate from the density profile according to equation (2) would be possible, it was found to be very prone to noise in the number 1s densities. To circumvent this problem and reduce scattering, rates were estimated from the slope of a linear fit considering three measured density values at (t − τ), t and (t + τ) (see figure 2). Theoretical changing rates ${R}_{{\rm{sim}},{n}_{e}}(t)$ were simulated based on measured number densities ${n}_{1{\rm{s}}}(t)$ and T_e(t) for the respective frame. Note that no RBEs were solved for the 1s states.

Zoom In Zoom Out Reset image size

Because the previous model considered 1s states only as sources and sinks for population processes of other states, modelling of their changing rates demanded incorporation of some additional processes. Atomic collisions causing population of 1s states as well as de-population due to Penning ionisation were taken from [12]. Quenching of 1s states by molecular nitrogen was considered by rate constants from [15] (Ar $1{{\rm{s}}}_{5}$ and $1{{\rm{s}}}_{3}$) and [16] (Ar $1{{\rm{s}}}_{4}$ and $1{{\rm{s}}}_{2}$).

To estimate electron densities, changing rates were calculated for several values of n_e and the value showing best agreement with observed changing rates yielded the electron density. For verification, the process was performed for the 1s levels individually.

Densities of two metastable ($1{{\rm{s}}}_{3}$ and $1{{\rm{s}}}_{5}$) and two resonant ($1{{\rm{s}}}_{2}$ and $1{{\rm{s}}}_{4}$) 1s levels are depicted in figure 3. Similarly to previous observations, densities of all 1s states exhibited significant variations during the discharge cycle featuring decline during recombination and rise during the collisional part [4]. Low intensity of underlying argon emission lines in the 'dark/recombining phases' around $\tfrac{1}{2}\pi$ and $\tfrac{3}{2}\pi$ together with relatively constant emission from molecular nitrogen complicate reliable estimation of densities in this part (see figures 1 and 4). Hence estimated 1s densities exhibited notable scattering during the dark phases. Naturally, this effect was more pronounced when the amount of nitrogen in the feeding gas was increased. The problem was partly overcome by subtracting the superposed emission bands of nitrogen 1PS during spectra fitting in the dark phase. The gas temperature used for density calculations by self-absorption was assumed to be 350 K which corresponded to the rotational temperature found to agree best with the nitrogen 1PS emission bands.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Higher admixtures of nitrogen resulted in reduced densities of all 1s states. This trend can be explained by collisional quenching of argon 1s states by nitrogen. Similar observations were made before [17, 18].

The uncertainty of the method was estimated via a Monte-Carlo approach by calculating the densities from input data which was artificially scattered. The initial intensities were randomly scattered between 0% and ±5%. The standard deviation of the resulting densities was found to be highest in the dark phases. However, for most of the cycle and especially the collisional part standard deviation was around 10% for $1{{\rm{s}}}_{5}$ and $1{{\rm{s}}}_{4}$ as well as 15% for $1{{\rm{s}}}_{3}$ and $1{{\rm{s}}}_{2}$. Especially in the case of $1{{\rm{s}}}_{2}$ it was found to rise quickly as intensity dropped in the dark parts. This may very likely be accounted to the generally low density of this state.

Profiles for the temporal evolution of the electron temperature in all gas combinations are depicted in figure 5. Temperatures were estimated individually from densities of nine argon Paschen 2p states.

Zoom In Zoom Out Reset image size

Data quality exhibited similar trends as number density estimations of the 1s states with reduced confidence close to the 'dark phases' of the discharge. Considering that densities of the 1s states directly entered T_e estimation, this was likely caused by scattering of their values.

It appears noteworthy that individual estimations of T_e from different 2p states differed when nitrogen was added to the discharge. In particular, levels $2{{\rm{p}}}_{2}$ and $2{{\rm{p}}}_{8}$ were found to yield very high temperatures during the collisional phases while the other levels remained at lower temperatures, similar to the value for pure argon (see figure 5). This effect became more pronounced when more nitrogen was added to the discharge and underlines the impact of N₂ on argon population kinetics. Impact of superposed 1PS emission of nitrogen can be excluded as a cause for the observed deviation since its spectrum was modelled and subtracted from the measurement. Furthermore, its intensity was largely outperformed by argon emissions during the collisional phase of the discharge cycle. Hence, it may be assumed that quenching by nitrogen affected $2{{\rm{p}}}_{2}$ and $2{{\rm{p}}}_{8}$ more strongly than the other 2p levels. Similar observations were made before for the Paschen 1s levels of argon where a notable variation of the quenching constants was observed for the individual sub levels [15, 16].

No individual interaction cross sections of argon 2p levels with nitrogen were available, therefore this effect could not be incorporated by the model. Higher quenching rates for $2{{\rm{p}}}_{2}$ and $2{{\rm{p}}}_{8}$ caused the simulated density ratios, ${{n}}_{\mathrm{sim}}(2{{\rm{p}}}_{2})/{{n}}_{\mathrm{sim}}(2{{\rm{p}}}_{1})$ and ${{n}}_{\mathrm{sim}}(2{{\rm{p}}}_{8})/{{n}}_{\mathrm{sim}}(2{{\rm{p}}}_{1})$, to be higher than their measured values. Higher estimations for T_e were subsequently caused by the fact that $2{{\rm{p}}}_{1}$ is preferably populated by ground state excitation and therefore features a stronger increase in number density when T_e increases [19]. Hence, for $2{{\rm{p}}}_{2}$ and $2{{\rm{p}}}_{8}$ small population ratios could only be achieved by the presented CRM under the assumption of very high values for T_e. This problem may be overcome in future works when individual interaction constants for $\mathrm{Ar}(2{\rm{p}})\ +\ {{\rm{N}}}_{2}$ become available.

To reduce the effect of missing quenching constants on the following calculations in this work, electron temperatures estimated from $2{{\rm{p}}}_{2}$ and $2{{\rm{p}}}_{8}$ were removed from the calculation of the average value of T_e. The averaged value was subsequently used for estimation of the electron density.

As depicted in figure 5, no notable change in average electron temperature estimated from the remaining seven 2p states was observed when nitrogen admixture was increased. However, temporal profiles were found to vary with N₂ admixture, featuring less plateau-like shapes at higher additions (see figure 5). This variation was accompanied by a systematic change in overall density and light emission from 2p states (see figure 4). Their temporal profiles were found to drop significantly earlier for larger admixtures of nitrogen, resulting also in longer dark periods and a less plateau-like shape. Furthermore, overall light emission was significantly lower at higher admixtures.

The findings show that, apart from the reduced number of useful 2p levels, the presented method for electron temperature estimation is robust towards small additions of a reactive gas. This may be especially important when, unlike for nitrogen, interaction constants are unknown.

The influence of uncertainties in the argon 1s densities was tested by a worst-case evaluation, assuming a deviation by ±15%. Their effect on the results of the CRM was tested in the bright part of the discharge cycle in pure argon as well as argon with $2 \% \,{{\rm{N}}}_{2}$ and found to affect the resulting electron temperatures by about 5%. Furthermore, the impact of a deviation of T_gas by ±10% was evaluated in the same way. Here, the indirect effect of T_gas due to a change of the argon Paschen 1s densities was considered by reducing/increasing their densities by $\sqrt{10 \% }$ at the same time (see [5]). The variation caused T_e to vary by around 5%. Hence, the overall uncertainty of the estimated electron temperature is mostly defined by systematic deviation among the results from individual argon 2p states when the average value is estimated. From figure 5 they were found to scatter within approximately ±20% (not considering $2{{\rm{p}}}_{2}$ and $2{{\rm{p}}}_{8}$ for argon–nitrogen mixtures). However, this deviation is systematic and does not originate from scattering.

Electron densities estimated from the slope of the argon 1s states for two extreme cases ($0 \% \,{{\rm{N}}}_{2}$ and 4% N₂) are depicted in figure 6. Particular good agreement between the individually estimated densities of $1{{\rm{s}}}_{5}$ and $1{{\rm{s}}}_{4}$ was found during the collisional phases (${\rm{\Phi }}=\pi$ and ${\rm{\Phi }}=2\pi$). This may be accounted to a more reliable estimation of the changing rate compared to $1{{\rm{s}}}_{2}$ and $1{{\rm{s}}}_{3}$ due to their higher densities and generally better data quality (see figure 3). Electron density was found to drop for larger admixtures of N₂. This observation is in agreement with reduced 2p number densities in figure 4 and previous observations from Thomson scattering [20].

Zoom In Zoom Out Reset image size

To estimate the impact of the input parameters on the outcome of the n_e estimation the input values of ${T}_{e},\tfrac{{{\rm{d}}{n}}_{1{\rm{s}}}}{{\rm{d}}{t}}$ and T_gas were varied by ±20%, ±10% and ±10% respectively. Variations of n_e in the collisional phase were compared for pure argon as well as argon with $2 \% {{\rm{N}}}_{2}$. Assuming a ±20% deviation for T_e as a worst-case scenario, n_e was found to change by approximately a factor of 3. Variation of the changing rates and T_gas revealed only small disturbances of the resulting electron density (approximately 10%) which may be neglected considering the impact of uncertainties in T_e and the finite simulation step-width of n_e in figure 6 which was 20 steps per order of magnitude. In future works, an improvement of the modelling of the individual argon Paschen 2p levels (e.g. by improved cross sections for electron impact excitation) may reduce the systematic scattering of T_e among the individual 2p levels and significantly improve the quality of n_e.

While estimated values of n_e for different 1s states were in satisfying agreement during the collisional phases where electron impact was governing the population mechanics, they exhibited notable scattering during the rest of the cycle and no agreement was observed. In order to extend the estimation to the whole discharge cycle, relative changes in light emission intensity were utilized.

With the temporal profiles of n_e, T_e and n_1s known, absolute densities of all 2p states could be calculated during the collisional phase. Dividing the calculated absolute number densities by their observed densities yielded individual calibration factors for each level. With these factors evaluated during the collisional phase, absolute 2p state number densities could be reconstructed for the rest of the discharge cycle. Subsequently, electron densities were estimated from comparison of simulated and absolute 2p state densities at all frames. The corresponding results are depicted in figure 7.

Zoom In Zoom Out Reset image size