Abstract
We use the quantum correlations of twin beams of light to investigate the fundamental addition of noise when one of the beams propagates through a fast-light medium based on phase-insensitive gain. The experiment is based on two successive four-wave mixing processes in rubidium vapor, which allow for the generation of bright two-mode-squeezed twin beams followed by a controlled advancement while maintaining the shared quantum correlations between the beams. The demonstrated effect allows the study of irreversible decoherence in a medium exhibiting anomalous dispersion, and for the first time shows the advancement of a bright nonclassical state of light. The advancement and corresponding degradation of the quantum correlations are found to be operating near the fundamental quantum limit imposed by using a phase-insensitive amplifier.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Anomalous dispersion in dielectric media can lead to negative group velocities and superluminal propagation of classical optical pulses. This could, on first glance, seem to lead to a conflict with information (or Einstein) causality, but it is actually a natural consequence of the causal transfer function of atomic media [1]. One physical explanation that is sometimes given for the speed limitation on causal information transfer is that fundamental quantum processes will inevitably add sufficient noise to any communication channel to prevent information transfer faster than the speed of light [1–5]. Here we demonstrate the use of a bright, continuous-variable two-mode state of light that exhibits quantum correlations stronger than classical correlations to investigate the advancement of optical signals in fast-light media. Using the correlated fluctuations in twin beams generated by four-wave mixing (4WM), we study the degradation of the quantum correlations as a function of the group velocity advancement due to anomalous dispersion. We show that noise measurements on our experimental system behave in quantitative agreement with the theoretical predictions based on a quantum-limited phase-insensitive optical amplifier. These results suggest that when using phase-insensitive gain as the method for generating anomalous dispersion, fundamental added noise is a significant contributing factor to limiting the speed of information transfer.
Slow-light properties (or positive group indices) produce temporal delays that can be investigated using quantum-correlated twin beams as well [6–11]. These delays are produced while also adding noise, but without the same potential for controversy. Such slow-light media make it possible to delay optical pulses with a frequency bandwidth matched to the bandwidth of the normal dispersion by many pulse lengths. With the other sign of the dispersion, and fast-light media, the same physics of altered group velocities is at play [12–15], while the pulse advance is much more constrained and the fundamental role of the noise becomes important to study as well [1–5]. While there have been many experiments investigating the advancement of classical pulses, there are relatively few experiments that address this issue for a nonclassical state of light.
2. Fast light, quantum noise and the speed of information transfer
While some investigations have involved single-photon propagation in fast-light media [16–18], here we use a continuous-variable bright quantum state to probe a fast-light medium. Continuous-variable quantum states eliminate the need for photon-counting or number-resolving detection, and allow for high-efficiency direct detection schemes to be used. Due to the lack of experimental investigations in this regime, it is an open question whether or not quantum correlations such as entanglement or squeezing could be detected after propagation through a fast-light medium. One can imagine that, due to the noise added by the phase-insensitive gain during the propagation, the quantum state would be immediately degraded and the quantum correlations fully destroyed given any advancement. On the other hand, it might be possible for some degree of quantum correlation to survive, particularly for advancements short compared to the correlation times involved. In this paper, we address this question by sending half of a bipartite continuous variable quantum state through a fast-light medium. This signal consists of fluctuations on one mode of a bright, continuous-wave twin-beam state of light. This mode taken by itself exhibits intensity fluctuations that are much larger than the standard quantum limit. Due to the nature of the twin-beam state these random fluctuations are quantum correlated with the fluctuations in the other twin beam, which acts as a time reference against which we can calibrate the advancement. The intensity cross-correlation between the beams will be shifted in time, depending on the relative advancement of the signal beam fluctuations [11].
The semi-classical description of slow-light and fast-light propagation in atomic media is typically based on the expression for the refractive index of an atomic gas [19], which takes the form

where g is the gain coefficient, γ the linewidth, ω0 is the center angular frequency of an optical transition and  the angular frequency of the optical field (k is the accompanying wave vector). This results in the group index
the angular frequency of the optical field (k is the accompanying wave vector). This results in the group index  and the corresponding group velocity
and the corresponding group velocity  . In regions where the dispersion
. In regions where the dispersion  can be linearly expanded over a given bandwidth, optical pulses with matching frequency bandwidth can propagate nearly distortion free while being delayed or advanced relative to a pulse traveling through vacuum. This is quantified by the pulse peak delay
can be linearly expanded over a given bandwidth, optical pulses with matching frequency bandwidth can propagate nearly distortion free while being delayed or advanced relative to a pulse traveling through vacuum. This is quantified by the pulse peak delay

where L is the propagation length and c is the vacuum speed of light. There is no known physical limit for the possible delay of optical pulses (i.e. for ng > 1). The situation is different for advancing optical pulses (corresponding to ng < 1), where a large relative advancement could seem to be in conflict with the relativistic causality principle. The seeming conflict was quickly identified and resolved by Sommerfeld and Brillouin [20, 21], who showed that a superluminal group velocity in dispersive media cannot be used for any information transfer faster than c, and that the group velocity cannot be identified with the information velocity of light pulses, which is always strictly c.
Triggered by advancements in experimental fast-light systems, renewed discussions on the topic have appeared over time [12–15, 18, 22–27]. This led to new proposals to investigate the physical processes that actually work to prevent large pulse advances and superluminal signaling [1–5]. The usual discussion of (noiseless) classical signals being passed through a fast-light medium involves the discussion of analytic signals. While the peak of a pulse form may be advanced, it is said that any measurement of the faintest leading edge of the pulse, an analytic signal, will determine the following waveform. Thus, the information was transmitted well before the peak, or any other obvious part of the waveform. This, of course, implies that new information can only correspond to nonanalytic points in the waveform, which also corresponds to an infinite frequency bandwidth to accommodate any discontinuities in the waveform or its derivatives, which can never fit into the finite linear dispersion regions that we can create. While this tightly constrains the problems that can be discussed, the fact is that the tiniest of leading edges of a pulse waveform are never well defined in practice, and one cannot create analytic optical signals. At some point the signal is so small that noise dominates. Equivalently, the wave function of the optical pulse will contain less than a single photon, and can only be measured in a statistical sense. In this case quantum field noise as well as detector noise become fundamental to even defining the problem. In these scenarios the ability to discern signals is limited by the signal-to-noise ratio. States of light that correspond to classical distributions of fields and their fluctuations result in a noise floor referred to as the standard quantum limit, which is a limiting factor in how precisely one can make measurements. Coherent states of light fall into this category. The use of quantum states of light can allow measurements to go beyond this limit by lowering the noise floor. The bright twin-beam state of light used here exhibits this property, and results in a 2.5 dB reduction of noise below the shot noise limit [28]6.
3. Experimental scheme
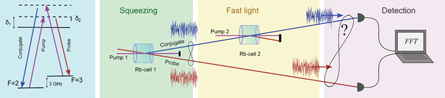
Our experimental scheme is shown in figure 1. Our system is based on 4WM in rubidium vapor, which is used to generate a pair of bright, strongly intensity-correlated twin beams. Each continuous-wave beam itself exhibits random intensity fluctuations, but the noise of the intensity-difference signal of the two photocurrents can be well below the standard quantum limit over a range of detection frequencies of a few MHz. The intensity-difference noise of the twin beams can be expressed using the mean photon numbers of the probe and conjugate modes,  and
and  [29, 30]
[29, 30]

This variance of the two-mode squeezed state can be smaller than the variance obtained with a pair of coherent state beams with equal intensity, which in this context defines the standard quantum limit.
Figure 1. Experimental scheme. On the left we show the relevant transitions for the 4WM scheme with the one-photon detuning δ1 and the two-photon detuning δ2. Continuous-wave intensity-squeezed twin beams (probe and conjugate beams) are created via the 4WM scheme in the first Rb cell. The conjugate beam is fed into a second 4WM process in the second Rb cell. The second pump beam's frequency is slightly detuned from the first pump beam, resulting in the probe experiencing little gain and strong anomalous dispersion. The photocurrent from the two detectors is digitized and subsequently the intensity-difference spectrum is analyzed via a discrete Fourier transformation and the relative time lag between the beams is determined by their intensity cross-correlation function.
Download figure:
Standard image High-resolution imageOne of the beams is sent through a second 4WM process such that it experiences a region of anomalous dispersion resulting from a nearby gain line, which has a spectral overlap with the typical range where intensity difference squeezing between the twin beams is present. Thus we can expect two things to occur:
- (i)Random intensity fluctuations on the beam that fit into the spectral bandwidth of the anomalous dispersion may be advanced according to equation (2), relative to their respective counterpart (the other beam of the twin-beam pair).
- (ii)The second 4WM process will inevitably introduce extra noise, which will either partially diminish or completely destroy the correlations between the twin beams.
The extra noise will consist partially of technical noise, such as scattered pump light, which can be minimized, and fundamental quantum noise. The 4WM process used to generate fast light is phase-insensitive, and as such we can quantify this added fundamental noise by using the input–output relations for an ideal phase-insensitive amplifier [31]. The expectation value of the output photon number  is thereby connected to the input photon number
is thereby connected to the input photon number  and the gain G by
and the gain G by

The variance of the output photon number is

With the expressions equations (3)–(5) the expected variance of the twin beams can be derived for the situation of one beam experiencing independent ideal phase-insensitive gain, which provides a lower bound for the added noise in this type of system. These expressions, along with the refractive index describing a Lorentzian gain line (equation (1), and the resulting group index and velocity), model the measured gain line and noise very well quantitatively, as seen in figure 2. While the simplified Lorentzian model for the gain line is used to provide intuition as to where to expect anomalous dispersion, the phase-insensitive amplification noise model's agreement with the experimentally measured values indicates that in the detuning region of interest the noise added to the advanced beam due to the nearby gain line is very close to the fundamental limit for an ideal phase-insensitive amplifier.
Figure 2. The red line represents a scan over the gain line in the fast-light cell versus the detuning of the fast-light pump laser (0 dB is equal to a gain of 1). We simultaneously recorded the intensity difference squeezing via balanced detection at a detection frequency of 750 kHz (green line). The input squeezing starts from the baseline of intensity difference squeezing −2.5 dB below the standard quantum limit, which is marked by 0 dB. The blue line shows ng − 1 derived from the measured gain profile. In the inset we show the region of interest for positive pump-detuning, where the intensity-difference noise is below the standard quantum limit and simultaneously the group index is less than zero. A Lorentzian fit is used to model the observed gain line profile, with the resulting group index following from equation (1) (and the resulting equations from equation (1)). This model is used to provide intuition as to where one can expect anomalous dispersion and negative group velocities. The noise model predicting the added noise is that of an ideal phase-insensitive amplifier, see equations (3)–(5). As expected, the experimentally measured noise is somewhat larger than the ideal scenario, and does not include subtraction of the scattered pump light, but agrees very well in the frequency region of interest (see inset).
Download figure:
Standard image High-resolution imageThe first stage of the experiment generates a pair of intensity difference squeezed beams via a 4WM process in 85Rb vapor [32–38]. The light beams involved are derived from a tapered amplifier system that is seeded with an external-cavity diode laser operating at 795 nm. A strong pump beam (200 mW) is sent through a vapor cell (heated to 114 °C), and a weak probe beam (20 μW), detuned by ≈ + 3 GHz, is injected at a small angle, as shown in figure 1. The 4WM gain amplifies the probe beam while traveling through the rubidium vapor and generates a conjugate beam at ≈ − 3 GHz relative to the pump and in a separate spatial mode. The coupled gain in the probe and conjugate modes results in two strongly intensity-correlated beams, which can be verified by direct intensity-difference detection with a pair of balanced photodiodes.
In the second step of the experiment one of the correlated beams is injected into a second 4WM process where the pump frequency is detuned by a few MHz relative to the pump of the first 4WM process, resulting in additional gain and accompanying dispersion of the injected beam. The frequency of the second pump beam can be detuned independently of the frequency of the first pump beam. A full scan of the resulting gain line is shown in figure 2, with a peak gain of 7.5 dB. The resulting gain line is of approximately Lorentzian shape and has a typical full-width at half-maximum (FWHM) of 10 MHz.
4. Results
In order to gain insight into which frequency regions one might expect to find both negative group velocities and quantum correlations in, an approximate model for the gain lineshape is used (equation (1)). The effect on the conjugate beam caused by traveling through this gain region can be described by a complex refractive index. The imaginary part describes the gain, which in turn adds noise proportional to the gain. This can be directly seen in the measured intensity-difference noise trace in figure 2. Here the gain is plotted in red. It is known that nonlinear optical susceptibilities do not always satisfy Kramers–Kronig relations applicable to linear dielectric media. For a nonlinear medium driven by a constant pump at a separate frequency from a weak probe, however, a related dispersion relation can be constructed. In this case, if probe saturation and self-action effects may be neglected, a dispersion relation may be written. The dashed red and blue lines show the gain line shape and the associated group index, respectively, and are based on the approximate dispersion model (equation (1) and the resulting equations). Here we have excellent agreement with the experimental data for all detunings. The real part of the refractive index describes the modified dispersion and the altered group index, shown in blue. The group index shows large positive values (slow light) near the center of the gain line, and negative values at the wings (fast light). The theoretically predicted noise (dashed green) associated with ideal phase-insensitive amplification is closely followed by the measured noise (solid green) in the low-gain regions. The noise added by phase-insensitive amplification (equations (3)–(5)) results in a good fit to the experimental data on the line wings, where the gain is low (which is the region of interest in the present experiment). The excess noise near the line center may be attributed to optical losses before the second rubidium cell which lead to an amplified intensity difference between probe and conjugate after the cell, as well as uncontrolled technical noise. Our further investigation concentrates on the region shown in the inset, where we have anomalous dispersion and reasonable agreement with the model for the added noise.
This characterization defines the detuning range for the pump used in the second 4 WM process, relative to the first 4WM pump frequency. We can expect the best chance for quantum correlations to survive when the additional gain is close to 1 and only a small amount of noise is added. This can be achieved in a region where the group index is negative on both wings of the gain line, at detunings ranging from −20 to −15 MHz and from 14.5 to 20 MHz. The gain in these regions varies from 1 to 1.25, with an experimental uncertainty of 0.05. This sets the center frequency and bandwidth for which we can expect group advancement of a transmitted signal. Frequency components of the signal that lie outside this frequency bandwidth experience a delay instead of an advancement.
A pair of amplified balanced detectors (detection efficiency 95%) allows us to directly monitor the amount of intensity difference squeezing. Additionally, by acquiring the individual time traces of the photocurrents generated by the twin beams we can measure the intensity correlation between the two beams, giving us information about the relative advancement of the beam that passes through the fast-light medium. All detectors are at equal distances from the first 4WM process to within a few centimeters, and thus the distances are not a limiting factor in determining the delay or advancement. The signals are recorded simultaneously with a high-speed digital oscilloscope (1 million points per trace, 2.5 giga-samples per second). We take a discrete Fourier transform of the difference signal to derive the spectral noise power of the intensity-difference output signal. The shot noise level is determined by sending a pair of coherent states with the same total optical power as the generated twin beams into the detection path. Our setup allows for intensity difference squeezing of −2.5 dB below the shot noise limit, mainly limited by the available pump power and scattered pump light.
From the two individual time traces i1 and i2 we calculate the intensity cross-correlation function [39, 40]

with a resolution of 400 ps, where i1, i2 denote the individual photocurrents. The maximum of the cross-correlation function when the 4WM process is off gives us the built-in lag in the arrival time of the correlations shared between probe and conjugate. When the second 4WM process is on we use the cross-correlation of the advanced beam with the reference twin beam as the signature for the presence of advancement or delay, which is given by

The sampling rate and length of our data acquisition are chosen such that it spans the correlation bandwidth given by the width of the 4WM gain line (≈ 20 MHz). As one can expect that different spectral parts of the full correlation spectrum may experience different group indices (even different in sign) we can selectively compute the cross-correlation function using only frequencies in the spectral region where we observe quantum correlations by applying a digital filter to the recorded data . The same filtering is applied to all of the data, in both the reference and fast-light cases. We use a Hanning window with the 3 dB roll-off points at 100 kHz and 3 MHz before the cross-correlation is computed. (We checked with different window types and widths that the observed effects are independent of the particular window choice.)
A typical example for the resulting intensity cross-correlation function is shown in figure 3. The red line shows the cross-correlation for the undisturbed input beam pair with a relative intensity squeezing of −2.5 dB. The green line shows an example for a cross-correlation between the beams, when one beam is passed near-resonantly (i.e. for a detuning of 6 MHz in figure 4) through the fast-light region of the second 4WM process. As can be seen in figure 4(a), for detunings of the second pump from approximately 0–15 MHz, the sign of the advancement/delay of the cross-correlation changes depending on whether or not the filtering is applied. If we apply the filter to restrict our analysis to the frequency region where there are quantum correlations, the resulting cross-correlation traces are advanced, as expected for the wing of a gain line. This frequency band is the region of interest, since we are investigating the effects of fast-light propagation on nonclassical light.
Figure 3. Intensity cross-correlation between probe and conjugate beam for a relative detuning of the two pump beams of 6 MHz. The cross-correlation shown is composed from the frequency spectrum from 100 to 3 MHz, where we also observe relative intensity squeezing. The correlations are advanced by 12 ns.
Download figure:
Standard image High-resolution imageFigure 4. (a) Observed delay of the cross-correlation function versus the detuning of the pump beam of the fast-light process relative to the pump beam that generates the squeezed beams. Pump powers are 200 and 300 mW, respectively. The pump diameters in the center of the first and second cells are ≈ 1 and ≈ 1.5 mm. The red points show the delay obtained by using the full spectrum of the correlated photon pairs (≈ 20 MHz). The green points show the cross-correlation for the noise bandwidth between 100 kHz and 3 MHz. (b) Simultaneously observed relative intensity squeezing in the bandwidth between 100 kHz and 3 MHz.
Download figure:
Standard image High-resolution imageTo demonstrate that squeezing between the two beams can be maintained when one of the beams is advanced, we set the detuning of the fast-light pump in the region where we can expect (from the line scan of figure 2) to have both significant anomalous dispersion and an extra gain not far above 1. In addition to the intrinsic added noise due to the phase insensitive gain, scattered pump light contributes an additional ≈ 0.2 dB of extra noise.
A sampling over a wide range of detunings of the fast-light pump, where the measured gain on the conjugate beam is less than 1.1 (0.41 dB), is shown in figure 4. Shown is the measured delay according to equation (7) versus two-photon detuning of the second pump (figure 4(a)) and simultaneously the measured squeezing integrated over the detection bandwidth between 100 kHz and 3 MHz (figure 4(b)). We obtain a relative advancement of up to 12 ns while still maintaining some relative intensity squeezing of the twin beams (see figure 4(b)). The measured data are quantitatively consistent with the additional noise being the minimum amount that must be added by a quantum-limited phase-insensitive amplifier (see equation (5)). Following equation (2), the advancement of 12 ns corresponds to a group index of the order of −150, which is in good quantitative agreement with the values shown in figure 2. Also the characteristic shape of the group index versus the two-photon detuning shown in figure 2 agrees well with a Lorentzian gain line model (see equation (1)).
We interpret this behavior as follows: the first 4WM process creates correlated photon pairs over a bandwidth of ≈ 20 MHz, which is determined by the spectral width of the gain lines for the probe and the conjugate of the 4WM process. The second 4WM process operates at a center frequency that is detuned a few MHz from the first process. Consequently, different parts of the spectrum will experience normal dispersion or anomalous dispersion when passing through the second cell. We can confirm this interpretation by filtering the photocurrents to the band from 100 kHz to 3 MHz, as shown in figure 4(a). The twin beams exhibit squeezing over this entire bandwidth, with a resulting cross-correlation FWHM of ≈ 165 ns. This spectral band also experiences only anomalous dispersion for detunings of the second pump greater than 3 MHz, and the resulting cross-correlation is advanced. For detunings of the fast-light pump greater than 15 MHz the advancement of the cross-correlation is not much affected by the choice of bandwidth, as here the full bandwidth of the photon pairs generated in the first 4WM process fits into the region of anomalous dispersion of the second 4WM process. For zero detuning we reproduce an experimental situation similar to the one described in [11], where most of the correlations are delayed and strongly degraded by added noise. In this case the spectral region of the quantum correlations that exhibit slow light is closer to the center of the gain line and therefore suffers from excess noise.
5. Conclusion
In summary, we have performed an experiment in which we sent one arm of a two-mode squeezed state through an atomic medium with anomalous dispersion. We have shown that the noise added due to the advancement using this system operates near the fundamental limit imposed by using a phase-insensitive amplifier as the fast-light medium. To the best of our knowledge, we presented the first direct measurement of the quantum limited noise penalty of a fast-light medium. Additionally, the present experiment shows that it is, in principle, possible to advance one of the two modes in a bipartite quantum state and still maintain some degree of nonclassical correlation, albeit for short advances compared with the average correlation time involved. The effect demonstrated here can lead to a better understanding of the physical processes that contribute to the 'peaceful coexistence between quantum mechanics and relativity' [41]. An extension of this work would be to investigate the dispersive and noise properties of a phase-sensitive amplifier [42].
Acknowledgments
This work was supported by the Air Force Office of Scientific Research. UV acknowledges support from the Alexander von Humboldt Foundation. This research was performed while RG held a National Research Council Research Associateship Award at NIST. QG was supported by the Marie Curie IOF FP7 Program—(Multimem—300632).
Footnotes
- 6
We remind the reader that the entanglement property of a bipartite state does not allow superluminal signaling, cf [28], and this is not changed by including a delay or an advance in one beam path.