ABSTRACT
Dark matter (DM) halos of Sc–Im and dwarf spheroidal (dSph) galaxies satisfy scaling laws: halos in lower-luminosity galaxies have smaller core radii, higher central densities, and smaller velocity dispersions. These results are based on maximum-disk rotation curve decompositions for giant galaxies and Jeans equation analysis for dwarfs. (1) We show that spiral, Im, and Sph galaxies with absolute magnitudes MV > −18 form a sequence of decreasing baryon-to-DM surface density with decreasing luminosity. We suggest that this is a sequence of decreasing baryon retention versus supernova-driven losses or decreasing baryon capture after cosmological reionization. (2) The structural differences between S+Im and Sph galaxies are small. Both are affected mostly by the physics that controls baryon depletion. (3) There is a linear correlation between the maximum rotation velocities of baryonic disks and the outer circular velocities Vcirc of test particles in their DM halos. Baryons become unimportant at Vcirc = 42 ± 4 km s−1. Smaller galaxies are dim or dark. (4) We find that, absent baryon "depletion" and with all baryons converted into stars, dSph galaxies would be brighter by ∼4.6 mag and dIm galaxies would be brighter by ∼3.5 mag. Both have DM halos that are massive enough to help to solve the "too big to fail" problem with DM galaxy formation. (5) We suggest that there exist many galaxies that are too dark to be discovered by current techniques, as required by cold DM theory. (6) Central surface densities of DM halos are constant from MB ∼ −5 to −22. This implies a Faber–Jackson law with halo mass M ∝ (halo dispersion)4.
1. INTRODUCTION
The systematic properties of dark matter (DM) can help us to understand what it is made of and how it affects galaxy formation and evolution. Best known is the imperfect (Casertano & van Gorkom 1991) conspiracy (van Albada & Sancisi 1986; Faber 1987; Sancisi & van Albada 1987) between visible and dark matter to make almost flat, featureless rotation curves. It results from the need, in order to form stars, for baryons to dissipate inside their DM halos until they self-gravitate (Blumenthal et al. 1986; Ryden & Gunn 1987; Flores et al. 1993). Rotation curve decompositions have been published for many galaxies. We first use these data to investigate the scaling laws for DM halos of late-type disk galaxies.
We show that DM halos in less luminous galaxies have smaller core radii rc, higher central densities ρ◦, and smaller central velocity dispersions σ. These correlations were first found by Athanassoula et al. (1987, hereafter ABP), Kormendy (1988, 1990), and Kormendy & Freeman (1996). Some of the correlations have been confirmed at least qualitatively by, e.g., Burkert (1995), Persic et al. (1996, 1997), Verheijen (1997), Salucci & Burkert (2000), Borriello & Salucci (2001), Begum & Chengalur (2004), Graham et al. (2006), Spano et al. (2008), Kuzio de Naray et al. (2008), de Blok et al. (2008), and Plana et al. (2010). The most thorough discussion to date is by Kormendy & Freeman (2004). This paper updates that work.
DM scaling laws are analogous to the fundamental plane relations for elliptical galaxies (Lauer 1985; Djorgovski & Davis 1986, 1987; Dressler et al. 1987; Faber et al. 1987; Djorgovski et al. 1988; see Kormendy & Djorgovski 1989 for a review), and they are interesting for the same reason: they provide new constraints on galaxy formation and evolution. Implications are discussed in Section 9.
For the giant galaxies, we estimate the halo parameters by decomposing their H i rotation curves V(r) into contributions from their visible matter and their DM halos (Carignan & Freeman 1985; van Albada et al. 1985). As rotation velocities become smaller for fainter galaxies (Tully & Fisher 1977), our faintest galaxies with absolute magnitudes  become pressure supported and rotation curve decompositions are no longer possible. We can still derive the central densities of the DM halos from their density and velocity dispersion profiles via the Jeans equations, but we cannot directly measure the DM core radii rc and velocity dispersions σ for these faint systems. In this paper, we use both rotation and velocity dispersion data to study the properties of DM halos over a large range of galaxy luminosities.
become pressure supported and rotation curve decompositions are no longer possible. We can still derive the central densities of the DM halos from their density and velocity dispersion profiles via the Jeans equations, but we cannot directly measure the DM core radii rc and velocity dispersions σ for these faint systems. In this paper, we use both rotation and velocity dispersion data to study the properties of DM halos over a large range of galaxy luminosities.
Only Sc–Im and dwarf spheroidal (dSph) galaxies are included, except in Figure 10. We omit E–Sbc galaxies because of the effects of their bulge components. (1) The rotation curve decompositions for these galaxies involve two visible components with different geometries and different unknown mass-to-light ratios M/L. They are therefore less reliable. (2) Baryonic gravitational compression of the DM can significantly modify the halo DM density distribution when the visible mass density is high (e.g., Sellwood & McGaugh 2005). Although many Sa–Sbc galaxies do satisfy the DM correlations, others deviate in the sense of small rc and large ρ◦ (ABP; Kormendy 1988, 1990; Jardel et al. 2011). This is especially true for elliptical galaxies (Thomas et al. 2009; Thomas 2010; Bender et al. 2015). We cannot be sure that Sc–Im galaxies are unaffected by baryonic compression, but their halos are the most nearly "pristine" (that is, uncompressed) that we are able to measure.
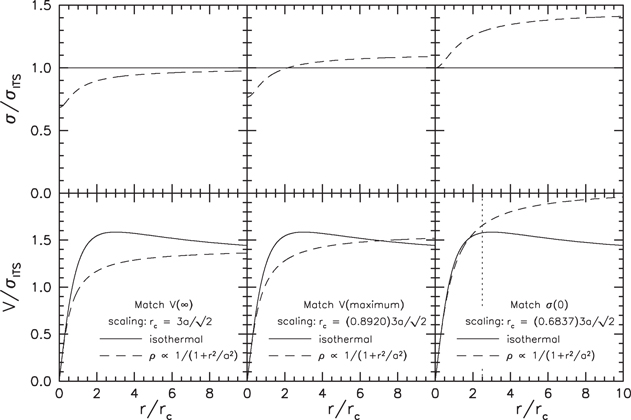
Figure 1. Rotation curves (bottom) and velocity dispersion profiles (top) for the isothermal and analytic (PITS) halos normalized to the velocity dispersion σITS of the ITS. The analytic halo is scaled in r and V so that both models have the same central density and asymptotic outer rotation velocity (left), maximum rotation velocity (middle), and central velocity dispersion (right). In the bottom-right panel, the analytic and isothermal halos have similar rotation curves out to r/rc ≃ 2.5 (vertical dotted line), i.e., over the radius range of typical H i rotation curves. However, the two models extrapolate very differently as 
Download figure:
Standard image High-resolution imageRoad map: Sections 2 and 3 discuss the measurement of DM parameters, our choice of Sc–Im galaxies, and calibration of DM parameters determined using the analytic "pseudo-isothermal sphere" DM model to parameters determined using the nonsingular isothermal sphere. They are necessarily long. Readers who are primarily interested in results can skip, especially on a first reading, to Section 5's discussion of Figure 4 and correlation fit Equations (21)–(33). Section 6 discusses the measurement of DM densities ρo in dSph and dwarf Magellanic irregular (dIm) galaxies. Readers who are primarily interested in results can skip to Section 7 on the estimation of baryon depletion in dwarf galaxies. Section 8 contains two additional observational results. Section 9 summarizes our conclusions.
2. MEASUREMENT OF DM HALO PARAMETERS BY ROTATION CURVE DECOMPOSITION
2.1. Technique
The H i rotation curves of giant spirals typically extend out to a few tens of kiloparsecs in radius. Over this region, we model the DM halo as a nonsingular isothermal sphere (ITS) with velocity dispersion σ, central density ρ◦, and core radius rc. These three parameters are not independent; they are related by

(e.g., King 1966), where G is the gravitational constant. In the core of the ITS ( ), the density is roughly constant and the rotation curve of a massless disk is
), the density is roughly constant and the rotation curve of a massless disk is

For  the density ρ(r) of the ITS is ∝ r−2 and the rotation curve becomes flat,
the density ρ(r) of the ITS is ∝ r−2 and the rotation curve becomes flat,

If we have rotation data only in the inner V ∝ r part of the ITS, then we can measure ρ◦ but not rc or σ. Therefore ρ◦ is often the only halo parameter that we can measure for low-luminosity galaxies in which the rotation data do not extend to large radii. On the other hand, if the measurements extend out into the flat part of the rotation curve, then all three halo parameters can be estimated.
In low-luminosity Sc–Im galaxies, the visible matter contributes only a small fraction of the total mass. In brighter systems, the visible matter appears to dominate the radial potential gradient in the inner parts of the disk, and a multicomponent mass model (stars + gas + DM) is needed. The shape of the rotation curve due to the visible stellar matter is calculated from the observed surface brightness distribution assuming that the mass-to-light ratio is constant with radius. Values of M/L are adjusted to fit as much of the inner rotation curve as desired. The contribution from the H i gas, including a correction for He, is calculated separately. Molecular gas is assumed to follow the light distribution (e.g., Regan et al. 2001), so its contribution is included in the adopted M/L. Given the total rotation curve Vvis due to the potential of the visible matter, the DM halo rotation curve is  A mass model such as the nonsingular ITS is then fitted to VDM to derive the halo asymptotic velocity
A mass model such as the nonsingular ITS is then fitted to VDM to derive the halo asymptotic velocity  rc, and ρ◦.
rc, and ρ◦.
Rotationally supported late-type dwarfs are especially suitable for rotation curve decomposition. They are easy to measure: they are rich in H i, and the gas extends to large radii. They are easy to interpret: they contain a disk and a halo but not a bulge. They are interesting: they give leverage to the derivation of any correlations between DM parameters and luminosity. And they are relevant: the visible matter density is low, so it has not greatly modified the halo parameters.
A note on total DM masses: The referee emphasizes that the total mass of a DM halo with a ρ ∝ r−2 density profile does not converge. However, analysis of cold dark matter (CDM) n-body simulations shows that the volume density is best fitted by an "Einasto profile" (Einasto 1965; Einasto & Haud 1989) d ln (ρ(r))/d ln r ∝  with n ≃ 5.8 (Merritt et al. 2006). Its total mass converges as
with n ≃ 5.8 (Merritt et al. 2006). Its total mass converges as  Point 3 in Section 2.2 notes that Navarro et al. (1996) functional forms with outer ρ ∝ r−3 are also popular in fitting n-body halos, even though they—unlike Einasto halos—logarithmically diverge in mass as
Point 3 in Section 2.2 notes that Navarro et al. (1996) functional forms with outer ρ ∝ r−3 are also popular in fitting n-body halos, even though they—unlike Einasto halos—logarithmically diverge in mass as  We find that the above Einasto and Navarro–Frenk–White (NFW) profiles agree remarkably well over ∼7 orders of magnitude in ρ before the Einasto profile decreases more rapidly at the largest r. Comparison of decompositions made with isothermal, NFW, and Einasto DM halos is postponed to a future paper. Here we note that, in using isothermal halos over modest ρ ranges at small r, we do not mean to imply that they should be extrapolated to large radii where total masses diverge. In fact, we mention total DM masses only briefly in this paper.
We find that the above Einasto and Navarro–Frenk–White (NFW) profiles agree remarkably well over ∼7 orders of magnitude in ρ before the Einasto profile decreases more rapidly at the largest r. Comparison of decompositions made with isothermal, NFW, and Einasto DM halos is postponed to a future paper. Here we note that, in using isothermal halos over modest ρ ranges at small r, we do not mean to imply that they should be extrapolated to large radii where total masses diverge. In fact, we mention total DM masses only briefly in this paper.
2.2. Our Assumptions
Lake & Feinswog (1989) point out that few observations of rotation curves reach large enough radii to determine halo parameters if measurement errors are interpreted strictly. Further assumptions are required.
1. We assume that observed rotation curves that become flat stay flat at larger radii.
2. The mass-to-light ratio of the disk is unknown and cannot be determined from the rotation curve alone. As van Albada et al. (1985) showed, halo parameters and disk mass-to-light ratios are degenerate. A wide range of DM and disk parameters can give a good fit to the observed rotation curve. As the amount of visible mass is reduced, the required central DM density increases and its core radius decreases. Their extreme models (van Albada et al. 1985, Figures 4 and 8) provided almost equally acceptable fits to the rotation curve. At one extreme is a maximum disk, with the largest M/L that does not require the halo to have a hollow core. This assumption gives the minimum ρ◦ for the halo and the maximum value of rc consistent with the rotation curve. The other extreme has a disk with M/L = 0.
Fortunately, we have additional constraints. Disk masses cannot be arbitrarily small. The presence of bars and spiral density waves requires that disks be self-gravitating. ABP used Toomre's (1981) swing amplifier theory and the properties of the observed spiral structure (i.e., two arms but not one) to constrain the density of the disk. For 18 of 21 Sc–Im galaxies, the outcome favored maximum disk decompositions. We adopt maximum disk decompositions, recognizing that this is still a controversial subject.
Many authors try to settle the question of maximal versus submaximal disks using a range of dynamical observations and arguments. Some evidence favors maximal disks (e.g., Visser 1980; Taga & Iye 1994; Sackett 1997; Debattista & Sellwood 1998, 2000; Bosma 1999; Salucci & Persic 1999; Sellwood & Moore 1999; Weiner et al. 2001; Athanassoula 2004; Weiner 2004). Other evidence suggests that some disks are submaximal (e.g., Bottema 1993, 1997; Courteau & Rix 1999; Herrmann & Ciardullo 2009; Bershady et al. 2011; van der Kruit & Freeman 2011). Our choice of maximum disks affects only giant galaxies; dwarfs are so dominated by DM that M/L uncertainties have little effect. With submaximal disks, DM parameter correlations with galaxy luminosity would be shallower. The referee notes that, with M/L = 0 minimum disks (see Figure 10 of de Blok & McGaugh 1997), the sense of the ρo(MB) and rc(MB) correlations in Section 5 would be reversed. This would be inconsistent with constraints summarized in Section 9.11. In any case, minimum disks cannot make self-gravitating structures such as bars and density waves.
3. For the DM halo model, we adopt the nonsingular (cored) ITS (Section 2.1). Ryder et al. (2004) and de Blok (2010) review the well-known collision (Moore 1994) between the cuspy central density profiles ρ(r) seen in CDM simulations and the observational evidence that dwarf galaxies (at least) have flat cores. The Navarro et al. (1996, 1997; NFW) profile, with its ρ ∝ r−1 cusp at small radii, has its roots in DM-only simulations and is still widely used. See Diemand & Moore (2011) for a review of cusp structure. CDM simulation papers widely agree that CDM halos are expected to have cuspy centers rather than isothermal-like cores (e.g., Moore et al. 1998, 2001; Klypin et al. 2001, 2011; Colín et al. 2004; Diemand et al. 2004, 2005, 2008; Hayashi et al. 2004; Navarro et al. 2004, 2010; Klypin et al. 2011).
De Blok (2010) reviews the controversial observational situation. The observed rotation curves, especially for fainter galaxies, usually indicate that their DM halos have cores. Some authors have tried to "save cusps" by emphasizing systematic uncertainties like beam smearing in the H i rotation data and noncircular motions in the higher-resolution optical rotation data; these could create the appearance of a core. Over the past decade, rotation curve data and mass modeling have improved, and cores in the DM halos of dwarf and low-surface-brightness galaxies are consistently favored (e.g., de Blok & Bosma 2002; Marchesini et al. 2002; Weldrake et al. 2003; Gentile et al. 2004, 2009; de Blok et al. 2008; Oh et al. 2008, 2011a, 2011b; Spano et al. 2008; Donato et al. 2009; Plana et al. 2010; Chen & McGaugh 2010; Walker et al. 2010). De Blok (2010) concludes that almost all dwarf disk galaxies that have been studied have cored halos. The situation is less clear for giant disks like M101. A careful review by Sellwood (2009) concludes that the core-cusp problem is unsolved for giant galaxies. We note, however, that hydrodynamic simulations of galaxy formation with feedback (e.g., Governato et al. 2010) show that violent feedback from rapid star formation in the inner regions of disk galaxies can transform a cusped DM halo into a cored halo. We adopt cored isothermal halos in this paper.
The dSph galaxies are in pressure equilibrium, and the dynamical analysis is based on stellar radial velocities rather than rotation. Many authors use Jeans equation analyses. Another promising approach is Schwarzschild (1979, 1982) orbit superposition modeling of the observed spatial and velocity distributions of individual stars in dSph galaxies. The Nuker team orbit superposition code (e.g., Gebhardt et al. 2003; Richstone et al. 2004; Thomas et al. 2004, 2005; Siopis et al. 2009) has been applied to six dSph companions of our Galaxy by Jardel and Gebhardt. They conclude that these galaxies have a heterogeneous range of DM profiles: dSph galaxies with cores include Fornax (Jardel & Gebhardt 2012) and probably Carina (Jardel & Gebhardt 2013); dSph galaxies with cuspy, NFW-like profiles include Draco (Jardel et al. 2013) and Sextans (Jardel & Gebhardt 2013); and Sculptor is uncertain but most consistent with an NFW profile (Jardel & Gebhardt 2013); see Jardel (2014) for a summary. However, (1) the features in the line-of-sight velocity distributions that differentiate between best-fit NFW profiles and best-fit cored halos are far from obvious in these papers; (2) in the formally NFW galaxies, cored halos are excluded by not much more than 1σ, and (3) the cored halo machinery used in our paper provides an adequate fit to all the data. Other authors using different analysis techniques favor cored halos for dSph galaxies (e.g., Amorisco & Evans 2012).
In Section 6.1, Figure 5, and the
In the present paper, we do not further discuss the issue of halo cores and cusps, other than to note again that baryonic physics can affect CDM density distributions and produce cores when none were present initially. The most promising mechanism is rapid ejection of most baryons via star formation feedback (Navarro et al. 1996; Gnedin & Zhao 2002; Governato et al. 2010; de Souza et al. 2011; Oh et al. 2011a; Di Cintio et al. 2014; Madau et al. 2014). The idea is especially compelling for tiny dwarfs. Surface brightnesses decrease rapidly with decreasing galaxy luminosity. Galaxies like Draco and UMi are so DM dominated that if the present stars were spread out into primordial gas with a density profile like that of the stars, then—given metal-poor stellar populations like those of M/L ∼ 2 globular clusters but measured dynamical M/L ∼ 102—that gas would not self-gravitate. It would be difficult to engineer instabilities that make stars. The suggestion has long been that these galaxies contained more baryons when the stars formed and then blew most of the baryons away via the first supernovae (see Kormendy 1985, 1987b; Kormendy et al. 2009; Kormendy & Bender 2012 for the observations, and Dekel & Silk 1986 for the theoretical concepts). Observational evidence that is consistent with this picture is presented in Section 8.
For the purposes of this paper, the difference between cored and cusped DM profiles is relatively benign. The history of work on the luminous density profiles of elliptical galaxies is relevant here. Ground-based observations of the central parts of ellipticals were made during the 1980s and revealed results that include the fundamental plane correlations (Kormendy 1984, 1987b, 1987c; Lauer 1985). Then the Hubble Space Telescope (HST) showed that the brightest ellipticals have cores with surface brightnesses  at small radii, with m ≃ 0–0.25 (e.g., Lauer et al. 1995). Earlier ground-based observations of core radii and central densities proved to probe the same physics as HST observations of break radii and densities (Kormendy et al. 1994). Thus, most of the ground-based results remained valid. In the future, when the details of halo density profiles are better known, we expect that our DM parameters will continue to measure the relevant physics. Our core radius may turn out to be a measure of a break radius in the halo density profile, and the central density will probably be a measure of some average density inside the break radius, independent of whether the halos have flat cores or not.
at small radii, with m ≃ 0–0.25 (e.g., Lauer et al. 1995). Earlier ground-based observations of core radii and central densities proved to probe the same physics as HST observations of break radii and densities (Kormendy et al. 1994). Thus, most of the ground-based results remained valid. In the future, when the details of halo density profiles are better known, we expect that our DM parameters will continue to measure the relevant physics. Our core radius may turn out to be a measure of a break radius in the halo density profile, and the central density will probably be a measure of some average density inside the break radius, independent of whether the halos have flat cores or not.
2.3. Galaxy Selection Criteria
For rotation-dominated galaxies, DM halo parameters are taken from rotation curve decompositions in the literature. While some authors use the nonsingular ITS model for their dark halos, most others use a simple analytic pseudo-isothermal sphere. These models are significantly different, and we need to derive the transformations between DM halo parameters from the two models (Section 3), using the nonsingular ITS as our reference model. Other than this transformation, we have made as few changes as possible, only adjusting the data to a uniform distance scale and adopting the following selection criteria:
1. As mentioned above, we include only late-type, Sc–Im and dSph systems. It now seems likely that dSph galaxies are related to late-type galaxies. The structural parameters of their visible matter are similar to those of the lowest-luminosity Im galaxies (Kormendy 1985, 1987c; Binggeli & Cameron 1991; Ferguson & Binggeli 1994; Kormendy & Bender 2012; see also Figure 9 of this paper). Most of the classical nearby dSph galaxies show evidence of star formation in the past 1–8 Gyr (e.g., Aaronson & Mould 1985; Mighell 1990; Mighell & Butcher 1992; Lee et al. 1993; Beauchamp et al. 1995; Weisz et al. 2011; see Da Costa 1994; Mateo 1998; Tolstoy et al. 2009 for reviews). At the time of their most recent star formation, they would have been classified as irregular galaxies (Kormendy & Bender 1994, 2012). See also Section 9.6 in this paper. We therefore include Sc–Im and dSph galaxies in the same parameter correlation diagrams.
2. Most galaxies with inclinations i < 40° are excluded. As Broeils (1992) remarks, H i rotation curves are less accurate for galaxies that are nearly face-on. Similar criteria were used by, e.g., Begeman (1987) and de Blok et al. (2008). Oval distortions (Bosma 1978; Kormendy 1982; Kormendy & Kennicutt 2004) can lead to incorrect estimates of inclinations for the more face-on galaxies. We retained four i < 40° galaxies from ABP (M101, NGC 5236, NGC 6946, and IC 342) because they provide leverage at high luminosities. Although we did apply this inclination cut to our sample, it turns out that most nearly face-on galaxies satisfy the DM parameter correlations.
3. The rotation curves must extend to large enough radii to constrain the DM parameters. The adopted criterion is that the observed rotation curve extends to at least 4.5 exponential scale lengths of the disk. For a self-gravitating exponential disk, the rotation curve peaks at 2.2 scale lengths (Freeman 1970), so the rotation curve contribution from the disk drops significantly over 4.5 scale lengths. A flat observed rotation curve then gives useful constraints on the DM parameters. The particular choice of 4.5 scale lengths allows us again to keep a few galaxies that provide leverage at high luminosities. This radius criterion was not rigidly applied: we retained a few galaxies whose rotation data extend out to 3.5–4.4 scale lengths, because the DM halo was dominant enough so that halo parameters were well determined. These galaxies are DDO 127, DDO 154, DDO 168, NGC 247, NGC 925, and IC 2574. We found that the radius cut is important. Without it, the sample is larger and mostly consistent with the correlations, but with larger scatter than seen in Figures 2–4 and 6–7. This selection criterion is an important difference between the present work and previous investigations of DM scaling laws.
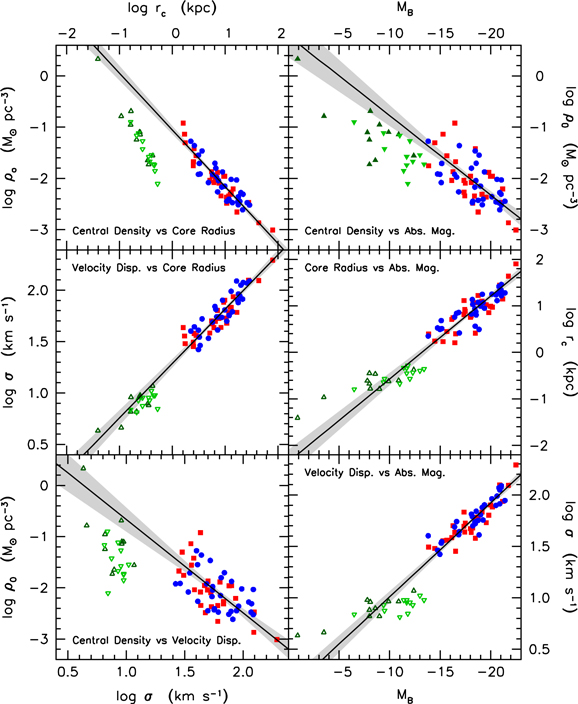
Figure 2. Correlations of DM central density ρ◦ (top), core radius rc (middle), and particle velocity dispersion σ (bottom) with galaxy absolute magnitude MB. The left panels show results derived using isothermal halos ("ITS") in rotation curve decompositions of Sc–Im galaxies (blue points from Table 1). The right panels show results (red points) derived using pseudo-isothermal halo models ("PITS"; Equation (3)). The PITS points are calibrated to the ITS points as in Kormendy & Freeman (2004; Equations (5)–(7) here). The purpose of this figure is to correct the 2004 calibration to provide the final calibration that we apply to PITS decomposition results to get the parameters that are listed as PITS-derived results in Table 1 and that are plotted in Figures 3–9. To derive the corrections, we calculate symmetric, least-squares fits (Tremaine et al. 2002) in each panel (blue and red lines) and then shift the PITS points vertically until the fits agree at MB = −18. NGC 3274 and NGC 5204 (overplotted with black cross) are omitted from the PITS fits here to keep the slopes of the red and blue lines similar. They are retained in the final correlation plots and fits. The recalibrations resulting from this figure are Equations (14)–(16). The final, combined 2004 and 2011 calibrations are Equations (17)–(19).
Download figure:
Standard image High-resolution imageFigure 3. Superposition of Figure 2 correlations derived from ITS decompositions (blue points) and from PITS decompositions (red points) after recalibration of the latter using Equations (14)–(16). For 14 galaxies, we have both ITS and PITS decompositions. They are identified with blue and red crosses, and their averages are shown in black.
Download figure:
Standard image High-resolution imageFigure 4. Final DM parameter correlations for the rotationally supported Sc–Im galaxies after recalibration of PITS results (red points) to those derived using isothermal halos (blue points). The lines are symmetric, least-squares fits (Tremaine et al. 2002) to all of the points. We estimate measurement errors by comparing the DM parameters for 15 galaxies with two independent decompositions (see text). The mean standard deviations are 
 and
and  The intrinsic scatter in each parameter is then estimated and iterated until we get the most consistent possible values that imply a reduced χ2 = 1 in all six fits. These intrinsic scatter values are σ(MB) = 0.77 ± 0.03,
The intrinsic scatter in each parameter is then estimated and iterated until we get the most consistent possible values that imply a reduced χ2 = 1 in all six fits. These intrinsic scatter values are σ(MB) = 0.77 ± 0.03, 
 and
and  These values are probably dominated by the different assumptions (e.g., on disk M/L ratios) made in the heterogeneous collection of rotation curve decomposition papers. Nevertheless, they are upper limits on the true intrinsic scatter in the DM correlations. The final fits shown are Equations (21)–(26) with 1σ uncertainties shaded.
These values are probably dominated by the different assumptions (e.g., on disk M/L ratios) made in the heterogeneous collection of rotation curve decomposition papers. Nevertheless, they are upper limits on the true intrinsic scatter in the DM correlations. The final fits shown are Equations (21)–(26) with 1σ uncertainties shaded.
Download figure:
Standard image High-resolution imageFigure 5. Gaussian distributions of surface density in two dwarf galaxies. The top panel shows the radial distribution of star-count density n against major-axis radius for the Carina dSph galaxy (data from Irwin & Hatzidimitriou 1995). The bottom panel shows the radial distribution of H i surface density ΣHi against major-axis radius for the DDO 210 dIm galaxy (derived from Young et al. 2003). In this (ln ΣHi, r2) plane, a Gaussian distribution is a straight line. The solid straight lines show Gaussian fits to these two galaxies. Because Plummer models are often used to represent the surface densities of dwarf galaxies, the dotted curve in the bottom panel shows the best-fit Plummer model for comparison.
Download figure:
Standard image High-resolution imageFigure 6. DM parameter correlations for Sc–Im galaxies (red and blue points from Figure 4 and Table 1), dSph galaxies (green triangles from Table 2), and dIm galaxies (upside-down green triangles from Table 2). For dSph and dIm galaxies, ρ◦ is a measure of the DM and hence is plotted with filled symbols in the top right panel. However, rc and σ are visible-matter parameters and so are plotted with open symbols in the other panels. The straight lines (from Figure 4) are least-squares fits to the Sc–Im galaxies only. Note: Gilmore et al. (2007) also find that dSph ρ◦ values fall below the extrapolation of the correlation for brighter galaxies (see their p. 949, left column).
Download figure:
Standard image High-resolution imageFigure 7. DM parameter correlations for Sc–Im galaxies, dSph galaxies (green triangles), and dIm galaxies (upside-down green triangles) as in Figure 6 but with the dSph and dIm galaxies shifted in MB,  , and
, and  to bring them on to the scaling laws for the Sc–Im galaxies. The goal is to estimate (1) the likely effect of baryon loss from these faint galaxies and (2) the typical ratios of the baryonic to DM values of
to bring them on to the scaling laws for the Sc–Im galaxies. The goal is to estimate (1) the likely effect of baryon loss from these faint galaxies and (2) the typical ratios of the baryonic to DM values of  and
and  assuming that the DM halos of the dwarfs follow the scaling relations for the Sc–Im galaxies. The shifts for the dSph and dIm galaxies are, respectively,
assuming that the DM halos of the dwarfs follow the scaling relations for the Sc–Im galaxies. The shifts for the dSph and dIm galaxies are, respectively,  and
and 
 and
and  and
and  and
and  These shifts lead to DM central surface densities that are independent of luminosity (Figure 8).
These shifts lead to DM central surface densities that are independent of luminosity (Figure 8).
Download figure:
Standard image High-resolution image4. In the late stages of the selection process, various "sanity checks" on physically plausible decompositions resulted in the omission of additional objects:
(i) Some recent papers do not use maximum disk V(r) decompositions but rather use disk M/L ratios based on optical or infrared colors (e.g., using Bell & de Jong 2001). These decompositions are usually plausible, but we need to be consistent in using maximum disk decompositions if we hope to measure the scatter in the DM parameter correlations.
(ii) A few galaxies were omitted because the adopted M/L was much too large for a blue, star-forming disk (e.g., UGC 5716 with M/LB ≃ 8.9 on our distance scale; van Zee et al. 1997).
(iii) Several authors model the DM halo with the pseudo-isothermal sphere (PITS; see Section 3). The PITS has a well-defined central density but differs significantly in its structure and rotation curve from the nonsingular ITS. Galaxies were omitted when the published PITS ρ◦ and rc values implied asymptotic outer rotation velocities that are much larger than the outermost velocities that are actually observed.
(iv) NGC 1705 (Meurer et al. 1998) and NGC 2915 (Meurer et al. 1996; Elson et al. 2010) were omitted because (1) intense starbursts drive strong winds that may affect the inner rotation curves; (2) H i beam smearing in NGC 1705 affects the central V(r) point that, in essence, determines M/LB; and (3) both galaxies are sometimes classified as amorphous (I0) rather than as Magellanic irregulars (Im). See, however, Elson et al. (2010, 2013).
(v) The edge-on galaxy NGC 801 is classified as Sc in de Vaucouleurs et al. (1991, hereafter RC3), but photometry in Kormendy & Bender (2011, see Figures S6 and S7) shows that it has a pseudobulge that makes up 23% of the total light. This is clearly evident in the photometry of Kent (1986), Andredakis & Sanders (1994), and Courteau (1996). Including the pseudobulge in any decomposition makes the results very uncertain. NGC 801 was the lowest-ρ◦, largest-rc point in Figure 4 of Kormendy & Freeman (2004). Here we conclude by comparison with (P)B/T ratios in Simien & de Vaucouleurs (1986) that NGC 801 is a misclassified Sbc. On this basis only—and not because of its DM parameters—we discard it everywhere except in Figure 8.
Figure 8. Product  surface density of DM halos as a function of observed (not shifted) absolute magnitude. Symbols are as in Figures 2–7. The straight line shows the mean surface density for the Sc–Im galaxies. The dark and light green points are for dSph and dIm galaxies, respectively. The
surface density of DM halos as a function of observed (not shifted) absolute magnitude. Symbols are as in Figures 2–7. The straight line shows the mean surface density for the Sc–Im galaxies. The dark and light green points are for dSph and dIm galaxies, respectively. The  values for their DM halos are derived from the
values for their DM halos are derived from the  values for their stellar or H i distributions by applying shifts as given in the key and explained above.
values for their stellar or H i distributions by applying shifts as given in the key and explained above.
Download figure:
Standard image High-resolution imageFigure 9. Comparison of DM halo parameters from Figure 7 with visible matter structural parameters from Kormendy & Bender (2012). Central projected densities are plotted for DM halos; effective stellar surface densities Σe = Σ(re) are shown for visible components. Here re is the radius that encloses half of the light of the component. Surface brightnesses are converted to stellar surface densities using mass-to-light ratios M/LV = 8 for ellipticals, 5 for classical bulges and S0 disks, and 2 for spiral galaxy disks, Im galaxies, and Sph galaxies. These are typical values that approximate the results of dynamical or stellar population studies (e.g., Mateo 1998; Cappellari et al. 2006, 2013a, and the rotation curve decomposition papers). Their uncertainties are not large enough to affect our conclusions. For example, M/L ratios for the stellar parts of spiral and irregular galaxies can be smaller than 2, but we neglect the contribution of H i gas, and this partly compensates for the presence of young stars.
Download figure:
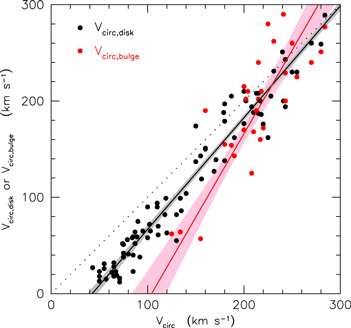
Standard image High-resolution imageFigure 10. Maximum rotation velocity of the bulge Vcirc,bulge (red points) and disk Vcirc,disk (black points) given in bulge-disk-halo decompositions of observed rotation curves whose outer, DM rotation velocities are Vcirc. The dotted line indicates equality of the maximum rotation velocities of the dark and visible matter. Every red point has a corresponding black point, but many galaxies are bulgeless, and then only a disk was included in the decomposition; for these, the plot shows only a black point. This figure illustrates that the "rotation curve conspiracy," essentially Vcirc,bulge ≃ Vcirc,disk ≃ Vcirc for the halo (Bahcall & Casertano 1985; van Albada & Sancisi 1986; Sancisi & van Albada 1987), happens mostly for galaxies with Vcirc ∼ 200 km s−1. The lines are least-squares fits with each variable symmetrized around 200 km s−1 (Equations (46) and (47)) and with 1σ uncertainties shaded. The correlation for bulges is steeper than the one for disks; thus bulges disappear at Vcirc ∼ 104 ± 16 km s−1. This figure is adapted from Figure S2 in Kormendy & Bender (2011).
Download figure:
Standard image High-resolution image(vi) Finally, the ultrathin, edge-on Sd galaxy UGC 7321 was omitted because its rotation curve is better fitted with a NFW DM profile than by a cored halo (O'Brien et al. 2010). Given the form of V(r) for an NFW halo, UGC 7321 deviates from our DM correlations in the direction of small rc and large ρo.
In addition to the selection cuts, we adopt the following procedures to make parameters from different sources be as consistent with each other as possible.
More accurate distances are now available than the Kraan-Korteweg (1986) Virgocentric flow model distances used in Kormendy & Freeman (2004). We adopt distance measurements and sources as listed in Table 1 (Section 4). Accurate distances based on primary standard candles (e.g., Cepheid variables) are available for 62% of our sample. Another 12% of our sample galaxies are far enough away (D = 37–84 Mpc) that distances based on recession velocities and a Hubble constant of H◦ = 70 km s−1 Mpc−1 (Komatsu et al. 2011) are accurate. For the remainder of our sample, a more complicated strategy was required (see Notes to Table 1).
Table 1. Dark Matter Halo Parameters for Rotationally Supported Galaxies
| Galaxy | D | Source | MB |

|

|

|
DM | Source |
|---|---|---|---|---|---|---|---|---|
| (Mpc) | (km s−1) | (M⊙ pc−3) | (kpc) | Model | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| NGC 24 | 8.1 | 1 | −18.10 | 1.8129 | −1.8020 | 0.8242 | ITS | Chemin et al. (2006) |
| NGC 45 | 7.1 | 1 | −18.54 | 1.7404 | −2.0444 | 0.8728 | ITS | Chemin et al. (2006) |
| NGC 55 | 2.17 | 1 | −19.25 | 1.7559 | −2.4073 | 1.0719 | ITS | Puche et al. (1991) |
| NGC 55 | 2.17 | 1 | −19.25 | 1.8732 | −2.5263 | 1.2498 | PITS | Broeils (1992) |
| NGC 247 | 3.65 | 1 | −19.17 | 1.8785 | −2.5158 | 1.2471 | ITS | ABP |
| NGC 247 | 3.65 | 1 | −19.17 | 1.8424 | −2.5836 | 1.2476 | PITS | Broeils (1992) |
| NGC 253 | 3.94 | 1, 2 | −21.03 | 2.0734 | −2.3110 | 1.3396 | ITS | ABP |
| NGC 925 | 9.2 | 1, 2 | −20.17 | 1.8813 | −1.9606 | 0.9719 | PITS | de Blok et al. (2008) |
| NGC 300 | 2.00 | 1 | −18.43 | 1.7348 | −2.1715 | 0.9348 | ITS | ABP |
| NGC 300 | 2.00 | 1 | −18.43 | 1.8294 | −2.2403 | 1.0650 | PITS | Broeils (1992) |
| NGC 598 | 0.85 | 1, 2 | −19.00 | 1.8075 | −2.1518 | 0.9937 | ITS | ABP |
| NGC 598 | 0.85 | 1, 2 | −19.00 | 1.9417 | −2.0961 | 1.0971 | PITS | Corbelli (2003) |
| NGC 1003 | 9.2 | 1 | −19.15 | 1.8327 | −2.3112 | 1.0986 | PITS | Broeils (1992) |
| NGC 1560 | 3.45 | 1, 2 | −17.36 | 1.8327 | −2.2712 | 1.1131 | PITS | Broeils (1992) |
| NGC 2366 | 3.19 | 1, 2 | −16.53 | 1.4521 | −1.6732 | 0.3990 | PITS | Oh et al. (2011b) |
| NGC 2403 | 3.22 | 1 | −19.39 | 1.9025 | −1.8747 | 0.9502 | ITS | ABP |
| NGC 2403 | 3.22 | 1 | −19.39 | 1.8964 | −2.0379 | 1.0288 | PITS | Broeils (1992) |
| NGC 2998 | 71.1 | 3, 4 | −21.76 | 2.0926 | −2.8692 | 1.6375 | PITS | Broeils (1992) |
| NGC 3109 | 1.34 | 1, 2 | −16.44 | 1.6884 | −1.9226 | 0.7600 | ITS | Jobin & Carignan (1990) |
| NGC 3109 | 1.34 | 1, 2 | −16.44 | 1.8581 | −2.1709 | 1.0561 | PITS | Broeils (1992) |
| NGC 3198 | 13.6 | 1, 5 | −20.53 | 1.8976 | −2.4601 | 1.2379 | ITS | Blais-Ouellette et al. (1999) |
| NGC 3198 | 13.6 | 1, 5 | −20.53 | 1.9020 | −2.4966 | 1.2611 | PITS | Broeils (1992) |
| NGC 3274 | 6.5 | 1, 2 | −16.46 | 1.6360 | −0.9209 | 0.2067 | PITS | de Blok & Bosma (2002) |
| NGC 3359 | 19.5 | 3, 4 | −20.90 | 1.9128 | −2.6141 | 1.3300 | ITS | ABP |
| NGC 3621 | 6.64 | 1 | −19.99 | 1.9020 | −1.9591 | 0.9919 | PITS | de Blok et al. (2008) |
| NGC 3726 | 18.6 | 1, 6 | −21.19 | 1.9367 | −2.2067 | 1.1503 | PITS | Verheijen (1997) |
| NGC 3741 | 3.19 | 1 | −13.86 | 1.4928 | −1.7555 | 0.3958 | Burkert | Gentile et al. (2007) |
| NGC 3917 | 18.6 | 1, 6 | −19.82 | 1.8023 | −1.8857 | 0.8554 | PITS | Verheijen (1997) |
| NGC 4183 | 18.6 | 1, 6 | −19.56 | 1.7300 | −2.3661 | 1.0233 | PITS | Verheijen (1997) |
| NGC 4244 | 4.49 | 1, 2 | −18.77 | 1.7528 | −2.4294 | 1.0771 | ITS | ABP |
| NGC 4395 | 4.61 | 1, 2 | −18.19 | 1.7889 | −2.4741 | 1.1362 | ITS | ABP |
| NGC 4455 | 7.8 | 1 | −17.49 | 1.7245 | −2.0936 | 0.8815 | PITS | de Blok & Bosma (2002) |
| NGC 5033 | 17.2 | 3, 4, 7 | −21.06 | 2.0885 | −2.5221 | 1.4598 | ITS | ABP |
| NGC 5033 | 17.2 | 3, 4, 7 | −21.06 | 1.9393 | −2.2059 | 1.1507 | PITS | Broeils (1992) |
| NGC 5204 | 4.65 | 1, 2 | −16.90 | 1.6435 | −1.3596 | 0.4176 | ITS | Sicotte & Carignan (1997) |
| NGC 5204 | 4.65 | 1, 2 | −16.90 | 1.6190 | −1.0419 | 0.2502 | PITS | Swaters et al. (2003) |
| NGC 5236 | 4.47 | 1, 2 | −20.63 | 1.9890 | −2.0209 | 1.1125 | ITS | ABP |
| NGC 5457 | 7.2 | 2, 9 | −21.41 | 1.9450 | −2.4479 | 1.2775 | ITS | ABP |
| NGC 5585 | 7.2 | 1, 2, 10 | −18.47 | 1.7202 | −1.4656 | 0.5633 | ITS | Blais-Ouellette et al. (1999) |
| NGC 5585 | 7.2 | 1, 2, 10 | −18.47 | 1.7045 | −1.4426 | 0.5360 | PITS | Broeils (1992) |
| NGC 5907 | 15.15 | 11 | −20.82 | 2.0693 | −2.4750 | 1.4170 | ITS | ABP |
| NGC 5907 | 15.15 | 11 | −20.82 | 2.0473 | −2.1380 | 1.2246 | PITS | Miller & Rubin (1995) |
| NGC 6015 | 17.7 | 3, 4 | −20.12 | 1.9619 | −2.3587 | 1.2511 | ITS | Verdes-Montenegro et al. (1997) |
| NGC 6503 | 5.27 | 1, 2 | −18.57 | 1.8407 | −1.7056 | 0.8057 | ITS | ABP |
| NGC 6503 | 5.27 | 1, 2 | −18.57 | 1.7695 | −1.3832 | 0.5714 | PITS | Broeils (1992) |
| NGC 6822 | 0.50 | 1, 2 | −15.67 | 1.5596 | −1.5577 | 0.4488 | PITS | Weldrake et al. (2003) |
| NGC 6946 | 5.9 | 1, 2 | −21.06 | 2.0885 | −2.0322 | 1.2166 | ITS | ABP |
| NGC 7793 | 3.91 | 1, 2 | −18.86 | 1.6107 | −1.5467 | 0.4946 | ITS | Carignan & Puche (1990) |
| IC 342 | 3.28 | 2, 9 | −20.90 | 2.0488 | −2.2782 | 1.2988 | ITS | ABP |
| IC 2574 | 4.02 | 1, 2 | −18.24 | 1.6990 | −2.4480 | 1.0302 | ITS | Martimbeau et al. (1994) |
| UGC 191 | 17.8 | 3, 4 | −18.23 | 1.6773 | −2.4867 | 1.0310 | PITS | van Zee et al. (1997) |
| UGC 2259 | 9.2 | 1 | −16.63 | 1.7404 | −1.9768 | 0.8390 | ITS | Carignan et al. (1988) |
| UGC 2259 | 9.2 | 1 | −16.63 | 1.8456 | −2.0352 | 0.9778 | PITS | Broeils (1992) |
| UGC 2885 | 84.0 | 3, 4 | −22.50 | 2.2909 | −3.0104 | 1.9004 | PITS | Broeils (1992) |
| UGC 3174 | 8.1 | 1 | −15.29 | 1.5539 | −1.1367 | 0.2326 | PITS | van Zee et al. (1997) |
| UGC 4499 | 17.2 | 12, 13 | −18.08 | 1.6365 | −2.0805 | 0.7871 | PITS | Swaters et al. (2003) |
| UGC 5005 | 56.0 | 3, 4 | −18.00 | 1.6717 | −1.9561 | 0.7572 | PITS | de Blok & McGaugh (1997) |
| UGC 5764 | 7.1 | 1 | −14.47 | 1.4797 | −1.3038 | 0.2418 | PITS | van Zee et al. (1997) |
| UGC 6446 | 18.6 | 1, 6 | −18.49 | 1.5781 | −1.4200 | 0.4130 | PITS | Verheijen (1997) |
| UGC 6983 | 18.6 | 1, 6 | −18.76 | 1.7844 | −2.6574 | 1.2233 | PITS | Verheijen (1997) |
| UGC 11820 | 18.8 | 3, 4 | −17.44 | 1.6383 | −2.3430 | 0.9200 | PITS | van Zee et al. (1997) |
| UGC A442 | 4.27 | 1, 2 | −15.16 | 1.5441 | −1.7091 | 0.5112 | ITS | Côté et al. (2000) |
| ESO 287-G13 | 37.5 | 3, 4 | −20.90 | 2.0962 | −2.4740 | 1.4429 | PITS | Gentile et al. (2004) |
| ESO 381-G20 | 5.44 | 1 | −15.11 | 1.5315 | −2.0820 | 0.6829 | ITS | Côté et al. (2000) |
| ESO 444-G84 | 4.61 | 1, 2 | −13.82 | 1.6021 | −1.2755 | 0.3501 | ITS | Côté et al. (2000) |
| F568-V1 | 84.1 | 3, 4 | −18.40 | 1.7844 | −2.3460 | 1.0677 | PITS | Swaters et al. (2000) |
| F583-1,D584-4 | 36.9 | 3, 4 | −17.35 | 1.6861 | −2.0362 | 0.8145 | PITS | de Blok et al. (2001) |
| F583-1,D584-4 | 36.9 | 3, 4 | −17.35 | 1.7049 | −2.0454 | 0.8117 | PITS | Kuzio de Naray et al. (2008) |
| F583-1,D584-4 | 36.9 | 3, 4 | −17.35 | 1.6955 | −2.0408 | 0.8131 | PITS | mean of the above |
| DDO 127 | 6.9 | 1, 2 | −14.98 | 1.4230 | −1.9212 | 0.4941 | ITS | Bosma: Kormendy & Freeman (2004) |
| DDO 154 | 4.3 | 1, 2 | −14.75 | 1.4624 | −1.9142 | 0.5263 | ITS | Carignan & Purton (1998) |
| DDO 154 | 4.3 | 1, 2 | −14.75 | 1.4797 | −1.9460 | 0.5523 | PITS | Broeils (1992) |
| DDO 161 | 7.2 | 3, 4 | −16.84 | 1.6128 | −2.2648 | 0.8573 | ITS | Côté et al. (2000) |
| DDO 168 | 4.33 | 1, 2 | −16.27 | 1.7001 | −1.8688 | 0.7437 | PITS | Broeils (1992) |
| DDO 170 | 16.1 | 3, 4 | −16.15 | 1.5839 | −2.0398 | 0.7093 | PITS | Broeils (1992) |
Notes. Notes on distances—Adopted distances (Column (2)) are from sources listed in Column (3). To save space, most of our sources are compilations for many galaxies rather than the papers in which distance measurements are reported. Our primary source is the Kennicutt et al. (2008) list of galaxies in the local 11 Mpc volume. For D ≤ 11 Mpc, we use his distances whenever possible. Our second main source is the Karachentsev et al. (2004) Catalog of Neighboring Galaxies. These two sources almost always agree exactly; for our sample, they never disagree significantly. For 37 of our 60 galaxies (i.e., 62%), we use direct distance measurements in order of preference, as derived from Cepheid variables, from TRG, i.e., the tip of the red giant branch in the color–magnitude diagram, from brightest stars, or from membership in groups whose distances were measured either using the above direct methods or (in the case of UGC 4499) using surface brightness fluctuations in NGC 5866. Beyond this volume, five galaxies are in the Ursa Major cluster; we adopt D = 18.6 Mpc from Kennicutt et al. (2008) and Tully & Pierce (2000). When no direct measurement is available, we base D on a derivation of the large-scale flow field of galaxies as given in the listed sources. For four nearby galaxies, we adopt Kennicutt's flow-field distances based on a Hubble constant of H0 = 75 km s−1 Mpc−1. We then have a significant gap in distance between these objects at D = 7–8 Mpc and galaxies at D ≥ 15 Mpc for which we use flow-field distances from references (3) and (4). For the latter galaxies, we adopt H0 ≃ 70 km s−1 Mpc−1, consistent with Wilkinson Microwave Anisotropy Probe (WMAP) determinations (Komatsu et al. 2009, 2011). It may seem unrealistic to use different Hubble constants for nearby and distant galaxies, but Karachentsev & Makarov (1996) show that the apparent value of H0 reaches a maximum at D ∼ 2 Mpc and then decreases out to larger distances. Kennicutt et al. (2008) adopt the Karachentsev & Makarov flow-field solution, having engineered the currently best possible consistency between direct distance measurements and ones determined from flow fields. On the other hand, at large distances (seven galaxies have D = 37–84 Mpc), H0 is robustly smaller; we adopt the WMAP value. In between are seven galaxies at D = 15–19 Mpc for which flow-field results are particularly uncertain.
Distance references—(1) Kennicutt et al. (2008); (2) Karachentsev et al. (2004); (3) Mould et al. (2000) Virgocentric flow field solution as implemented in Reference (4); (4) NED "D (Virgo Infall only)" with H0 = 70 km s−1 Mpc−1; (5) Freedman et al. (2001); (6) Tully & Pierce (2000); (7) flow-field solution (3, 4) applied to the Can Ven Spur (group 43−1 in Reference 8); (8) Tully (1988); (9) Kormendy et al. (2010); (10) Drozdovsky & Karachentsev (2000); (11) flow-field D = 14.9 Mpc for group 44−1 (Reference 8) averaged with SBF D = 15.4 Mpc for group member NGC 5866 (reference 12); (12) Tonry et al. (2001); (13) in group 15−10 (reference 8) with NGC 2681, which has SBF D = 17.2 Mpc (reference 12).
Notes on DM models—The DM model used in rotation curve decomposition is given in Column (8). ITS means the nonsingular isothermal sphere; PITS means the pseudo-isothermal sphere (Equation (3)). NGC 3741 was analyzed (Gentile et al. 2007) using a Burkert (1995) analytic DM profile. The Burkert profile has a constant-density core and a volume density ρ(r) which closely resembles that of the PITS over a factor of >20 in density. We scaled its parameters to PITS parameters and then used our standard scaling to convert PITS parameters to ITS equivalents. All decompositions used in this paper are listed in the table, one per line. Their sources are given in Column (9). For the 15 galaxies with two independent decompositions—almost always ones with different DM models—comparison of the results gives estimates of the 1 s.d. measurement errors in the parameters; their averages are 
 and
and  These include errors in calibrating PITS to ITS results, but they do not include systematic errors that result if some disks are submaximal. These mean parameter errors for the 1/4 of our galaxies that have two decompositions are representative of the errors for galaxies that have only one decomposition.
These include errors in calibrating PITS to ITS results, but they do not include systematic errors that result if some disks are submaximal. These mean parameter errors for the 1/4 of our galaxies that have two decompositions are representative of the errors for galaxies that have only one decomposition.
DM parameters were corrected to our adopted distances by assuming that  and that ρ◦ ∝ D−2. This is not strictly correct, because gas and dynamical masses scale differently with distance. But the errors are small on the scales of Figures 2–4 and 6–7. Estimates of σ are independent of galaxy distance.
and that ρ◦ ∝ D−2. This is not strictly correct, because gas and dynamical masses scale differently with distance. But the errors are small on the scales of Figures 2–4 and 6–7. Estimates of σ are independent of galaxy distance.
Galactic absorption corrections are from Schlegel et al. (1998) as listed in NED. Total magnitudes BT are generally means of RC3 values listed in NED, values listed in the main catalog of Hyperleda, and values given in the "Integrated photometry" link at Hyperleda. For galaxies with rotation curve decompositions from van Zee et al. (1997), that paper is also the source of BT. Absolute magnitudes listed in Table 1 are corrected for internal absorption as in Tully & Fouqué (1985).
3. MATCHING PITS MODELS TO THE NONSINGULAR ITS
For rotation curve decompositions, a DM halo model is needed. The discussion in Section 2.1 was in terms of a nonsingular ITS model. Some authors use this model; then we use their derived parameters rc, ρ◦, and σ without modification. The density distribution and rotation curve of the ITS need to be calculated numerically, so some authors use the PITS model, whose density has the simple analytic form

No strong argument favors either the PITS or the ITS, other than that the ITS comes from a simple isotropic distribution function (e.g., King 1966). However, if we wish to use DM halo parameters from different sources, we need to work out how to scale the parameters for PITS decompositions to the system of parameters from ITS decompositions. While the PITS and ITS have a similar r−2 density distribution at large r, the PITS is otherwise not a good approximation to the ITS, and there is no exact scaling. For example, the bottom-left panel of Figure 1 shows how the rotation curve of the PITS tends to its value at large r from below, while the rotation curve of the ITS approaches its asymptotic value from above.
Figure 1 shows three possible ways to scale the rotation and velocity dispersion curves of the PITS to the ITS. In all three scalings, the central densities of the two models are the same. The panels differ in how radii and velocities are scaled. We will argue that the best scaling is intermediate between the middle and right panels of Figure 1.
In the left panels, the scaling in radius and velocity forces the rotation velocity and velocity dispersion to be the same at large radii. With this scaling, the core radius rc of the isothermal is  The velocity dispersions match only at large r, because an isotropic PITS is not isothermal. Its velocity dispersion is
The velocity dispersions match only at large r, because an isotropic PITS is not isothermal. Its velocity dispersion is

where x = r/a. For most galaxies, the H i distribution does not extend beyond about 2.5rc, and in this region the velocity dispersion of the PITS is less than that of the ITS. Similarly, the rotation curves match poorly in this region. We discard this scaling.
It seems more realistic to adopt a scaling of the PITS such that its rotation curve matches the rotation curve of the ITS most closely in the region where we have rotation data ( ). In the right panels of Figure 1, we make the velocity dispersion of the ITS equal to the central velocity dispersion σ(0) of the PITS, where
). In the right panels of Figure 1, we make the velocity dispersion of the ITS equal to the central velocity dispersion σ(0) of the PITS, where  Then
Then  and
and  This scaling preserves Equation (1) for the ITS,
This scaling preserves Equation (1) for the ITS, 
Although the PITS and ITS rotation curves are similar in the region where they are fitted to rotation data (Figure 1, bottom-right panel), this scaling gives a value of  for the PITS that is much larger than the observed velocity of the flat part of the rotation curve (top-right panel). We see from the literature that authors rarely extrapolate to such large (unobserved) maximum rotation velocities. This suggests that we should use a scaling as in the middle panel, in which
for the PITS that is much larger than the observed velocity of the flat part of the rotation curve (top-right panel). We see from the literature that authors rarely extrapolate to such large (unobserved) maximum rotation velocities. This suggests that we should use a scaling as in the middle panel, in which  for the PITS is scaled to the maximum, not the asymptotic, rotation velocity of the ITS. Then, when rotation curve decomposition is carried out using Equation (3) to derive the PITS parameters ρ◦, a, and
for the PITS is scaled to the maximum, not the asymptotic, rotation velocity of the ITS. Then, when rotation curve decomposition is carried out using Equation (3) to derive the PITS parameters ρ◦, a, and  we would adopt, for the corresponding ITS decomposition, rc = 1.8918a, the PITS value of ρ◦, and a halo velocity dispersion
we would adopt, for the corresponding ITS decomposition, rc = 1.8918a, the PITS value of ρ◦, and a halo velocity dispersion  Again, these parameters are related through Equation (1), as they should be for the ITS.
Again, these parameters are related through Equation (1), as they should be for the ITS.
In the end, after some experimentation, we adopted none of the above scalings.
Instead, we found enough rotation curve decompositions using the PITS and enough other decompositions using the ITS so that we could construct the DM parameter correlations separately for each model. By comparing these correlations, we empirically derive the best scaling between the two models. Using this method, Kormendy & Freeman (2004) derived the scalings  rc = 1.6154a, and
rc = 1.6154a, and  In Section 5, we begin with this scaling to construct Figure 2. We then derive corrections to the 2004 scaling based on the present galaxy sample (Equations (14)–(16)). Combining the 2004 and 2011 results provides the final scaling between the PITS and the ITS adopted in this paper: ρ◦ = 0.8554ρo,PITS, rc = 1.6591a, and
In Section 5, we begin with this scaling to construct Figure 2. We then derive corrections to the 2004 scaling based on the present galaxy sample (Equations (14)–(16)). Combining the 2004 and 2011 results provides the final scaling between the PITS and the ITS adopted in this paper: ρ◦ = 0.8554ρo,PITS, rc = 1.6591a, and  (Equations (17)–(19)).
(Equations (17)–(19)).
4. PARAMETERS OF DM HALO CORES
DM parameters are listed in Table 1. Columns (2) and (4) are the galaxy distance and its absolute magnitude corrected for internal extinction. The next three columns give the DM parameters; those derived using the PITS are scaled to the ITS via Equations (17)–(19). The last two columns give the DM model used and the source of the rotation curve decomposition.
5. DM HALO SCALING LAWS FROM ROTATION CURVE DECOMPOSITION
The correlations between halo rc, ρ◦, and σ and galaxy absolute magnitude MB are shown in Figures 2–4 for the rotationally supported Sc–Im galaxies. Figure 2 updates the Kormendy & Freeman (2004) calibration that we use to convert the results of PITS rotation curve decompositions to our best estimates of equivalent parameters derived using isothermal halos. Figure 3 shows why we adopt ITS results when decompositions using ITS and PITS halos are both available. Figure 4 combines all of the data as discussed below. Figure 6 adds measurements of the faint, pressure-supported Sph and Im galaxies as derived in Section 6.
Isothermals and pseudo-isothermals fitted to DM halos measure astrophysically equivalent parameters. However, they differ in detail. As discussed in Section 3, we need to calibrate parameters derived using PITS-based rotation curve decompositions to those given by decompositions that were made using isothermals. This calibration was carried out in Kormendy & Freeman (2004) by exactly the same method that we use below to update the calibration. We begin with the 2004 calibration,



Here we explicitly identify the parameters derived with the different DM models. This scaling is intermediate between the middle and right panels of Figure 1.
Applied to the PITS-based DM parameters derived by the references listed in Table 1, the 2004 calibration yields the correlations shown in red in the right panels of Figure 2. The ITS-based decompositions yield the correlations shown in blue in the left panels of Figure 2. The ITS-based parameters are as listed in Table 1.
The scatter about the correlations is slightly smaller in the left panels than in the right panels. This is an early sign (confirmed in Figure 3) that decompositions based on the ITS are better behaved. Such a conclusion is not surprising, given the slow rise of the PITS rotation curve to its asymptotic value (Figure 1). However, rotation curve decompositions based on isothermal and PITS models separately give essentially the same correlations. We have 32 galaxies with rotation curve decompositions based on isothermal DM halos and 41 with decompositions based on the PITS. Only 14 galaxies are common to both samples. So the correlations shown in the left and right panels of Figure 2 are largely independent. We want to combine the two samples. We do so by updating the scaling in the correlations in the right panels of Figure 2, as follows:
Least-squares fits to the correlations in the left panels of Figure 2 give



Least-squares fits to the correlations in the right panels of Figure 2 are



The two samples have essentially the same average absolute magnitude:  for objects analyzed with isothermals and
for objects analyzed with isothermals and  for those analyzed with the PITS. In the above, we therefore symmetrized the least-squares fits around MB = −18. As in Tremaine et al. (2002), we also symmetrized the other variables, i.e.,
for those analyzed with the PITS. In the above, we therefore symmetrized the least-squares fits around MB = −18. As in Tremaine et al. (2002), we also symmetrized the other variables, i.e.,  around −2,
around −2,  around 0.9, and
around 0.9, and  around 1.8. Then, requiring that the correlations agree at MB = −18 provides a correction to the 2004 scaling of the PITS results to those measured with the ITS,
around 1.8. Then, requiring that the correlations agree at MB = −18 provides a correction to the 2004 scaling of the PITS results to those measured with the ITS,



The change from the 2004 calibration is small. Combining Equations (5)–(7) with Equations (14)–(16) gives our final calibration,



This scaling is also intermediate between the middle and right panels of Figure 1. Equation (17) has been tweaked by about 1% to make the final ITS parameters satisfy exactly the usual relation for an isothermal (dropping the "ITS" subscripts),

Figure 3 superposes the ITS and PITS correlations from Figure 2 after recalibration of the latter. For 14 galaxies, we have rotation curve decompositions available using both halo models. Their parameters are identified with red and blue crosses. For each of these galaxies, the averages of the ITS and rescaled PITS parameters are shown in black. It is therefore easy to identify galaxies with two decompositions by finding triples of red, black, and blue points with the same MB and with the red and blue points overplotted with crosses.
One galaxy, F583-1, has two PITS decompositions. They agree well. Their means are also plotted in black.
Our initial intention was to use the above averages in our further analysis. But Figure 3 shows that, in almost every case when corresponding red and blue points disagree, the PITS points deviate more from the correlations. (The lines shown are symmetric least-squares fits to all the points using the mean parameters when there are two measurements for one galaxy. We do not adopt these fits, but we note that they are almost identical to the fits adopted in Figure 4.)
Correlation scatter is a combination of measurement errors and intrinsic scatter. When two different (ITS- and PITS-based) analysis machines are used on essentially the same data, then the intrinsic scatter is the same for both and it seems reasonable to conclude that larger observed scatter identifies the less reliable analysis machine. We therefore conclude that isothermal halos provide more reliable decompositions. So we adopt the ITS results—not the mean parameters—for the above 14 galaxies. For F583-1, we adopt the means of the two PITS decompositions.
We do, however, compare the ITS and scaled PITS parameters for the above 14 galaxies plus the two results on F583-1 to estimate the relative internal measurement errors in the parameters. Then, the 15 sets of mean parameters that are plotted in black in Figure 3 have mean standard deviations of 
 and
and  These values are used only as measurement errors that are input into the least-squares fits in Figure 4. Only their relative values are important.
These values are used only as measurement errors that are input into the least-squares fits in Figure 4. Only their relative values are important.
Figure 4 then shows the final DM correlation results, combining the ITS and scaled PITS parameters. When both are available, we use results based on isothermal halos. Based on 59 galaxies spanning 9 mag in MB, the correlations are quite robust. Uncertainties in rotation curve decomposition are unlikely to threaten them, although their slopes are still uncertain. The Figure 4 correlations are essentially identical to those found in Kormendy & Freeman (2004). Present results are more reliable for two reasons. New rotation curve decompositions published since 2004 have been added to our sample. More importantly, accurate distances based on primary standard candles (Cepheid variables, the tip of the red giant branch in the color–magnitude diagram, brightest stars, and the zero point of surface brightness fluctuations) are now available for 2/3 of our galaxies.
As in Figures 2 and 3, we fitted straight lines to the correlations in Figure 4 following the precepts of Tremaine et al. (2002). The two variables in each fit are treated symmetrically. Each variable is normalized approximately around its mean; the actual values used are given above Equations (14)–(16). Internal measurement errors as derived above are input, and the external scatter is estimated and iterated until the reduced χ2 = 1. This scatter (Figure 4 caption) is more likely to reflect heterogeneous data and decomposition procedures than it is likely to be a measure of any intrinsic, astrophysical scatter.
As derived, the least-squares fits to the points in Figure 4 are






where rc is measured in kpc, ρ◦ is measured in M⊙ pc−3, and σ is measured in km s−1.
In physically more transparent terms,







Here we have normalized parameters in terms of convenient round numbers that are, however, slightly different from the symmetrization values used in Equations (21)–(26). For example (Cox 2000), 109 LB⊙ is MB = −17.03, not MB = −18. The result is that we give up a little of the advantage (to the zero-point errors) in symmetrization; that is, the zero-point errors in Equations (27)–(33) are slightly larger than those in Equations (21)–(26) (see Tremaine et al. 2002 for a discussion). On the other hand, the equations are much easier to use, and the formal fitting errors are still small and in any case smaller than the systematic effects of different possible choices (e.g., nonmaximal disks) in the machinery of rotation curve decomposition.
Since we did not carry out the rotation curve decompositions, we cannot determine χ2 ellipses as "error bars" on the points in Figure 4. However, Vcirc is kept relatively fixed as decompositions explore the allowed range in (rc, ρo). Therefore, rc and ρo are strongly coupled, whereas σ is more robustly determined. Equation (2) tells us that the slope of the rising part of the DM rotation curve gives us the DM ρo:  Then the tilt in the χ2 ellipses is given roughly by
Then the tilt in the χ2 ellipses is given roughly by  In contrast, our Equation (21) is
In contrast, our Equation (21) is  Also, the parameter ranges for the observed correlations are much larger than the fit errors. We conclude that the derived DM parameter correlations are robust to errors in the rotation curve decompositions.
Also, the parameter ranges for the observed correlations are much larger than the fit errors. We conclude that the derived DM parameter correlations are robust to errors in the rotation curve decompositions.
6. CENTRAL DM DENSITIES OF DWARF GALAXIES
The faint dSph and dIm galaxies provide an opportunity to increase the range of galaxy luminosities over which we can examine at least the central densities of DM halos. If we can include the ultrafaint dSph galaxies with absolute magnitudes as faint as MB = −1, then the luminosity baseline for our DM scaling laws increases to about 22 mag. These tiny dwarfs do not rotate significantly. Instead, their stars are supported by their random velocities. So our tracers of the dynamics are the distribution and velocity dispersion of the stars. Similarly, in the smallest dIm galaxies, the H i is supported by its velocity dispersion and the gas provides the tracer. We will see that the method for estimating the central densities of the DM distributions in these two kinds of dwarfs is similar, although the tracers are different.
Early work by Aaronson (1983) and by Aaronson & Olszewski (1987) on stars in the Draco and UMi dSph galaxies showed that their velocity dispersions are much larger than expected if they are equilibrium systems that consist only of old, metal-poor stars. Their high velocity dispersions imply mass-to-light ratios of ∼100, not the globular-cluster-like M/L ∼ 2 that are expected for an old, metal-poor stellar population. It was already apparent at the time that their central DM densities  –1 M⊙ pc−3 were "shockingly high. Indeed, these are the highest central DM densities seen in any galaxy so far" (Kormendy 1987a). This was an early indication of the DM correlations shown in this paper.
–1 M⊙ pc−3 were "shockingly high. Indeed, these are the highest central DM densities seen in any galaxy so far" (Kormendy 1987a). This was an early indication of the DM correlations shown in this paper.
Much effort went into trying to find an escape from the conclusion that dSph galaxies are DM dominated. Early observational concerns about measurement errors, atmospheric effects in the most luminous stars, and unrecognized binary stars were gradually laid to rest. Now we have large samples of accurate radial velocities in many dSph galaxies; see Walker et al. (2009) for a compilation of dispersion data for classical and ultrafaint dSph galaxies.
Concerns were also raised about possible dynamical effects that might mimic the effects of DM. Some authors argue that dwarf spheroidal galaxies may be descendants of DM-free tidal dwarfs that were made in interactions of larger galaxies (Yang et al. 2014). This discussion continues. We do not review it here. We adopt the conventional interpretation that dSph galaxies are dominated by DM when their velocity dispersions are too high to be consistent with the masses of old stellar populations.
As the number of dSph galaxies with dispersion measurements has increased, escape routes that depend on rare events have become implausible. These include the suggestion (Kuhn & Miller 1989; Kuhn 1993) that the stars formerly in dSph galaxies are unbound because of Galactic tides, so we overestimate the masses of systems that are far from equilibrium. The required orbital resonance works best if the dispersion is only marginally larger than the escape velocity and if not too many systems need special engineering. But M/LV ratios of 10–100 (not ∼2) imply velocities that are inflated by factors of ∼2–6. Piatek & Pryor (1995), Oh et al. (1995), Sellwood & Pryor (1998), Klessen et al. (2003), and Wilkinson et al. (2004) argue convincingly that tides do not inflate velocity dispersions this much, especially not without producing detectable velocity gradients across the galaxies. This remains true even though apparently extratidal stars have been seen in some dSph galaxies (e.g., Irwin & Hatzidimitriou 1995; Piatek et al. 2001, 2002; Palma et al. 2003). And some dSph galaxies are too far from our Galaxy to be affected by tides (Mateo 1998; Mateo et al. 1998; Koch et al. 2007). All dSph galaxies with dynamical analyses now appear to be DM dominated. It has become difficult to argue that we get fooled by special circumstances.
One DM alternative is not addressed by the above arguments, Modified Newtonian Dynamics (MOND: Milgrom 1983a, 1983b, 1983c; Milgrom & Bekenstein 1987). While MOND continues to be debated (for reviews see Sanders & McGaugh 2002; Sellwood 2004), we adopt conventional Newtonian gravity and treat measurements of high velocity dispersions in dSph galaxies as detections of DM.
Large samples of accurate stellar velocities are now available for many dSph galaxies. We use them to estimate central DM densities via the Jeans equation. For the smallest dIm galaxies, rotation is negligible and the H i gas is supported mainly by its turbulent velocity dispersion. An H i study of the faint system GR8 with the Very Large Array by Carignan et al. (1990) used the radial distribution of H i velocity dispersion and surface density to estimate the central density of its DM halo. The H i in many dIm galaxies has now been observed with adequate spatial resolution. We follow the methods of Carignan and collaborators to derive the central densities of their halos.
6.1. Dwarf Spheroidal Galaxies
For dSph galaxies, the data that we can use to estimate the central DM densities are the projected stellar velocity dispersion profiles σ(R) and the surface density distributions I(R) of the stars. Even if we assume that the galaxies are spherically symmetric, these observables alone do not provide strong constraints on the central DM density. For example, we do not know the form of the underlying DM distribution or how the anisotropies of the stellar velocity distributions change with radius (see Walker et al. 2009 for more details). Some assumptions are needed. These should be consistent with the assumptions that we used in Section 2 for the spiral galaxies.
We use the spherical Jeans equation to estimate central DM densities from σ(R) and I(R). The measurable I(R) distributions for these low-surface-brightness dSph galaxies do not usually extend over a large range of surface density, and the star counts are often represented by simple approximations such as Plummer and King models. Because the Jeans equation involves derivatives of the density distribution, the outcome can be sensitive to details of how I(R) is modeled (e.g., Evans et al. 2009). We estimate the form of the baryon distribution I(R) expected in faint dwarf galaxies under a set of simple assumptions:
We assume that DM halos have constant-density cores. The issue is not settled (Section 2.2), though some authors support this assumption with their dynamical analyses (e.g., Amorisco & Evans 2012). We adopt this assumption to be consistent with our analysis of the Sc–Im galaxies.
How do the radial extents of the stars in dSph galaxies compare with the likely sizes of their DM cores? Typical half-light radii rh for dSph galaxies are a few hundred parsecs. From Table 1, the core radii for the DM halos in the faintest of our Sc–Im galaxies are about 1.6–2 kpc. Although the DM core radii of dSph galaxies may be smaller than those of faint, rotation-dominated Sc–Im systems, it seems reasonable to consider an approximation in which the stars are immersed entirely within the uniform-density core of the DM halo. Section 7 shows that this produces results that are internally consistent.
The projected velocity dispersion profile σ(R) also appears in the Jeans equation. The observed σ(R) profiles for the classical dSph galaxies are almost isothermal well beyond their half-light radii rh, out to R ∼ 1000 pc. Even for the ultrafaint system Seg 1, with rh ≃ 30 pc, the σ(R) profile is approximately isothermal out to about 60 pc. We assume (i) that each system is spherically symmetric, (ii) that the stars in a dSph galaxy lie entirely in the constant-density DM core, (iii) that the σ(R) distribution is isothermal, (iv) that the velocity distribution is isotropic, and (v) that the contribution of the stars to the total density is negligible. Then the spherical Jeans equation takes the simple form

where ρ* and σ* are the volume density and velocity dispersion of the stars, M(r) is the total mass enclosed within radius r, and ρ◦ is the central density of the DM. Then the stellar volume density is Gaussian,

and the volume density of the DM core is

The projected surface density Σ*(R) of a Gaussian volume density distribution ρ*(r) is also Gaussian with the same scale length a*. In fact, the star-count distributions of the classical dSph galaxies and some of the ultrafaint systems are well represented by Gaussians over most of their radial extent. As an example, Figure 5 shows the Gaussian radial profiles of the projected star counts for the Carina dSph system. Similar plots for all dSph galaxies used in this paper are shown in Figure 11 in the
Figure 11. Surface brightness profiles of the dSph galaxies used in this paper. They are plotted against radius2 so that the Gaussian fits shown are straight lines. Major-axis radius is in arcmin.
Download figure:
Standard image High-resolution imageFigure 12. H i column density profiles of the dIm galaxies used in this paper. They are plotted against radius2 so that the Gaussian fits shown are straight lines. Major-axis radius is in arcmin.
Download figure:
Standard image High-resolution imageTo compare the DM parameters of dSph galaxies with those for the rotationally supported disk galaxies, we use the halo density ρ◦ derived from the Gaussian star-count distribution and σ* via Equation (36) uncorrected for any contribution from the stars. While the near-isothermality of the velocity dispersion makes the analysis simpler, it does mean that there is little structure in the radial distribution of the kinematics from which one could estimate the core radius of the DM. At the present time, the central density is the only halo parameter that we can measure directly for dSph galaxies.
For the halo size parameter in rotationally supported disk galaxies, we used the core radius rc of the DM distribution derived from the shape of the rotation curve, following the King model scaling  In order to combine data for dark halos of galaxies over a wide range of luminosities, we would like to be able to measure King core radii for the halos of the dwarf galaxies. Because we cannot derive a size parameter for the DM in dSph galaxies from the stellar kinematics, we begin by tabulating the corresponding
In order to combine data for dark halos of galaxies over a wide range of luminosities, we would like to be able to measure King core radii for the halos of the dwarf galaxies. Because we cannot derive a size parameter for the DM in dSph galaxies from the stellar kinematics, we begin by tabulating the corresponding  value for their stellar distributions. King model fits are not available for all of our dSph galaxies, so we need to derive empirically the relation between the King
value for their stellar distributions. King model fits are not available for all of our dSph galaxies, so we need to derive empirically the relation between the King  and the Gaussian a* using eight dSph galaxies for which both lengths have been measured. The two lengths are tightly correlated:
and the Gaussian a* using eight dSph galaxies for which both lengths have been measured. The two lengths are tightly correlated:

With this calibration, Table 2 lists the distance, absolute magnitude, stellar velocity dispersion, DM core density, and stellar rc for 11 dSph companions of the Milky Way for which the star-count profiles are close to Gaussian. For CVn I and Coma 1, only a mean value of σ is available, and we have to assume that these systems are isothermal. We exclude two faint systems (Her and Wil 1) for which the star-count profiles are not Gaussian.
Table 2. Dark Matter Central Densities and Baryonic Velocity Dispersions and Core Radii for Spheroidal and Irregular Galaxies
| Galaxy | D | Source | MB | Source |

|

|

|
Source |
|---|---|---|---|---|---|---|---|---|
| (Mpc) | (km s−1) | (M⊙ pc−3) | (kpc) | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| Carina | 0.094 | NED | −8.0 | W09 | 0.820 ± 0.079 | −1.245 ± 0.158 | −0.676 ± 0.005 | IH95 |
| Draco | 0.076 | NED | −8.1 | W09 | 0.959 ± 0.057 | −0.687 ± 0.292 | −0.780 ± 0.101 | IH95 |
| Fornax | 0.138 | NED | −12.4 | W09 | 1.068 ± 0.033 | −1.557 ± 0.069 | −0.371 ± 0.006 | C05 |
| Leo I | 0.270 | NED | −10.9 | W09 | 0.964 ± 0.066 | −1.142 ± 0.133 | −0.606 ± 0.007 | IH95 |
| Leo II | 0.205 | NED | −9.0 | W09 | 0.820 ± 0.046 | −0.952 ± 0.094 | −0.786 ± 0.007 | C07 |
| Scl | 0.088 | NED | −9.9 | W09 | 0.964 ± 0.052 | −1.098 ± 0.105 | −0.622 ± 0.004 | IH95 |
| Sextans | 0.086 | NED | −8.6 | W09 | 0.898 ± 0.071 | −1.647 ± 0.145 | −0.466 ± 0.010 | IH95 |
| UMi | 0.069 | NED | −7.8 | W09 | 0.978 ± 0.055 | −1.101 ± 0.111 | −0.611 ± 0.007 | IH95 |
| CVn I | 0.218 | M08 | −8.0 | W09 | 0.881 ± 0.023 | −1.729 ± 0.061 | −0.448 ± 0.015 | M08 |
| Seg I | 0.023 | M08 | −0.9 | W09 | 0.633 ± 0.121 | 0.332 ± 0.247 | −1.408 ± 0.018 | M08 |
| Coma | 0.044 | NED | −3.5 | W09 | 0.663 ± 0.076 | −0.784 ± 0.153 | −0.967 ± 0.009 | M08 |
| GR8 | 2.13 | TRG | −12.0 | B06 | 0.954 ± 0.039 | −1.270 ± 0.080 | −0.565 ± 0.007 | B03A |
| SDIG | 3.21 | TRG | −11.7 | C00 | 0.954 ± 0.082 | −1.576 ± 0.165 | −0.450 ± 0.006 | C00 |
| Cam B | 3.34 | TRG | −11.8 | B03B | 0.845 ± 0.062 | −2.103 ± 0.090 | −0.281 ± 0.002 | B03B |
| Leo T | 0.42 | HB | −6.5 | I07 | 0.839 ± 0.063 | −0.900 ± 0.132 | −0.791 ± 0.015 | R08 |
| LGS3 | 0.76 | TRG | −9.4 | M98 | 0.929 ± 0.051 | −1.114 ± 0.114 | −0.642 ± 0.018 | Y97 |
| Leo A | 0.75 | TRG | −11.4 | B06 | 0.978 ± 0.059 | −1.853 ± 0.125 | −0.328 ± 0.014 | Y96 |
| DDO 210 | 0.99 | TRG | −11.0 | B06 | 0.813 ± 0.067 | −1.163 ± 0.107 | −0.675 ± 0.003 | Y03 |
| DDO 216 | 1.10 | TRG | −13.0 | Z00 | 1.021 ± 0.041 | −1.544 ± 0.076 | −0.396 ± 0.004 | Y03 |
| UGCA 292 | 3.60 | TRG | −11.7 | Z00 | 0.978 ± 0.046 | −1.742 ± 0.079 | −0.342 ± 0.008 | Y03 |
| DDO 53 | 3.60 | TRG | −13.4 | B06 | 0.978 ± 0.073 | −1.723 ± 0.133 | −0.358 ± 0.010 | B06 |
| UGC 7298 | 4.20 | TRG | −12.3 | B06 | 0.929 ± 0.066 | −1.670 ± 0.135 | −0.431 ± 0.009 | B06 |
| KK230 | 1.90 | TRG | −9.5 | B06 | 0.875 ± 0.029 | −1.426 ± 0.064 | −0.566 ± 0.010 | B06 |
Notes. Notes for dSph galaxies: Column (2) lists distances D based on stellar indicators from NED or M08 (Column (3)). Column (4) absolute magnitudes MB are from V-band luminosities in W09 (Column (5)) converted to B band adopting  for all systems. Column (6) velocity dispersions are from W09. Column (7)
for all systems. Column (6) velocity dispersions are from W09. Column (7)  is from Equation (36). Errors do not include distance errors. Column (8) lists
is from Equation (36). Errors do not include distance errors. Column (8) lists  for the stars, not the DM, derived from Gaussian lengths a* via Equation (37). Errors are from fits to Gaussian surface density distributions and do not include distance errors. Column (9) gives the sources of the star-count data. dSph galaxy references: C05—Coleman et al. (2005); C07—Coleman et al. (2007); IH95—Irwin & Hatzidimitriou (1995); M08—Martin et al. (2008); W09—Walker et al. (2009).
for the stars, not the DM, derived from Gaussian lengths a* via Equation (37). Errors are from fits to Gaussian surface density distributions and do not include distance errors. Column (9) gives the sources of the star-count data. dSph galaxy references: C05—Coleman et al. (2005); C07—Coleman et al. (2007); IH95—Irwin & Hatzidimitriou (1995); M08—Martin et al. (2008); W09—Walker et al. (2009).
Notes for dIm galaxies: Column (2) lists distances D based on stellar indicators from NED given in Column (3) (mostly TRG stars; in one case, horizontal branch stars). Column (4) absolute magnitudes MB are adopted from sources in Column (5) with some adjustment for distance. Column (6) H i velocity dispersions are adopted from sources in Column (9) with some adjustment for rotation. Column (7)  is from Equation (40) including the small contribution from rotation (not separately tabulated). Errors do not include distance errors. Column (8) lists
is from Equation (40) including the small contribution from rotation (not separately tabulated). Errors do not include distance errors. Column (8) lists  for the H i gas, not the DM, derived from Gaussian scale lengths a* via Equation (37). Errors are from fits to Gaussian surface density distributions and do not include distance errors. Column (9) gives the sources of the H i data. dIm galaxy references: B03A—Begum et al. (2003); B03B—Begum & Chengalur (2003); B06—Begum et al. (2006); C00—Côté et al. (2000); I07—Irwin et al. (2007); M98—Mateo (1998); R08—Ryan-Weber et al. (2008); Y96—Young & Lo (1996); Y97—Young & Lo (1997); Y03—Young et al. (2003); Z00—van Zee (2000).
for the H i gas, not the DM, derived from Gaussian scale lengths a* via Equation (37). Errors are from fits to Gaussian surface density distributions and do not include distance errors. Column (9) gives the sources of the H i data. dIm galaxy references: B03A—Begum et al. (2003); B03B—Begum & Chengalur (2003); B06—Begum et al. (2006); C00—Côté et al. (2000); I07—Irwin et al. (2007); M98—Mateo (1998); R08—Ryan-Weber et al. (2008); Y96—Young & Lo (1996); Y97—Young & Lo (1997); Y03—Young et al. (2003); Z00—van Zee (2000).
Download table as: ASCIITypeset image
6.2. Dwarf Irregular Galaxies: H i Equilibrium in a Uniform-Density DM Core
In the faintest dIm galaxies, the H i is supported by its velocity dispersion. We use the H i as our mass tracer. The H i velocity dispersion is usually observed to be close to isothermal and is likely to be isotropic. Assuming that the H i lies within the uniform-density core of the DM, arguments like the ones that we used for dSph galaxies lead us to expect that the distribution of projected H i surface density is again Gaussian. This is observed. The observed Gaussian length scale a* for the H i distribution and the observed H i velocity dispersion σ then give the central volume density of the DM halo core,  as above. As an example, Figure 5 shows the Gaussian profile of the H i surface density for the dIm galaxy DDO 210. Because Plummer models are a convenient and often-used represention of the surface densities in dwarf systems, the figure also shows the best Plummer model fitted to the H i surface density profile. The Gaussian provides a better fit when the surface density data extend over more than a few e-foldings. The near-Gaussian surface density distributions for the other dIm galaxies used in this paper are shown in Figure 12 (
as above. As an example, Figure 5 shows the Gaussian profile of the H i surface density for the dIm galaxy DDO 210. Because Plummer models are a convenient and often-used represention of the surface densities in dwarf systems, the figure also shows the best Plummer model fitted to the H i surface density profile. The Gaussian provides a better fit when the surface density data extend over more than a few e-foldings. The near-Gaussian surface density distributions for the other dIm galaxies used in this paper are shown in Figure 12 (
As we did for dSph galaxies, we consider the equilibrium of a spherical, isothermal, isotropic system of H i test particles in a uniform-density DM core. For the test particles, ρ*(r) is the volume density, Σ*(R) is the surface density, and c* is the isothermal sound speed or velocity dispersion. Some dIm galaxies show slow, near-solid-body H i rotation that we can readily include in our derivation. We take Ω* to be the angular velocity, assumed constant. For the DM, M(r) is the enclosed mass and ρ◦ is the core density.
The equation of hydrostatic equilibrium is then

and the H i volume density again is Gaussian,

The central volume density of the halo is

The correction to the dispersion c* from the channel spacing of the receiver (∼1.5 km s−1) is negligible. We estimate the error in the DM density ρ◦ derived from Equation (40) as follows. The contribution to ρ◦ from the  term is small. Then the error in ρ◦ is
term is small. Then the error in ρ◦ is

and the error in  is
is

The projected H i surface density is Gaussian with the same scale length a* as that of ρ* (Figures 5 and 12),

We need to correct a* for the telescope beam width. For a Gaussian telescope beam of width W = FWHM/2.355, the corrected value of a* for the galaxy is

If the error in a* from the least-squares fit is σa*, then the error in a*c is given by

As we did for dSph galaxies, we first use the core radius of the visible matter. We will see that this is much smaller than the core radius of the DM halo. We transform the beam-corrected H i Gaussian scale length a* (Equation (44), dropping the subscript c from here on) using the relation (Section 6.1)  The error in
The error in  is
is 
Table 2 lists the distance, absolute magnitude, H i velocity dispersion, DM core density, and rc of the H i distribution for 12 nearby dIm galaxies for which the dynamical contribution of the H i rotation is negligible and the H i surface density distribution is close to Gaussian. The effect of the beam correction is small: the correction increases  by between 0.01 and 0.11 and decreases
by between 0.01 and 0.11 and decreases  by between 0.003 and 0.04.
by between 0.003 and 0.04.
7. DM HALO SCALING LAWS INCLUDING DWARF GALAXIES: ESTIMATING THE BARYON LOSS IN DWARF GALAXIES
Figure 6 shows the combined scaling laws for the DM halos of late-type giant and dwarf galaxies. For the dwarfs, we here use the rc and σ values for the baryons, i.e., stars or H i (light and dark green symbols). With these values, the dwarfs lie below several of the scaling laws defined by the bright Sc–Im galaxies. This is not surprising, because there is no reason why the baryonic rc and σ values should be appropriate for the DM halos of the dwarfs. It is also likely that the dwarfs have lost a larger fraction of their baryons during their evolution than did the bright galaxies, because their potential wells are much shallower (Dekel & Silk 1986). Baryon loss is probably reflected in their faint MB values. This provides us with a way to estimate the baryon loss in the dwarfs and the relative values of the core radii and velocity dispersions of their baryons and DM, as follows:
We assume that dSph and dIm galaxies lie on the extrapolation of the DM scaling laws for bright galaxies. Very general arguments based on the initial spectrum of density fluctuations in the universe lead us to expect continuous DM scaling laws with no kinks (Section 9.10). Visible galaxy scaling laws are also continuous (Kormendy & Bender 2012; Figure 9 here) and show a baryon depletion sequence that starts at MV ≃ −18 and that is already well established at MB ≃ −14 where rotation curve decomposition fails. Physical reasons for this baryon depletion are well known (e.g., Dekel & Silk 1986; Klypin et al. 1999; Bullock et al. 2000). Figure 6 provides us with a plausible way to make these theoretical ideas quantitative; that is, a way to estimate the (we assume, continuously) decreasing baryon content in smaller galaxies.
We further assume that the central densities ρ◦ of the DM halos of all of our galaxies have been correctly measured. We then shift the MB, rc, and σ values for the dwarfs to move them onto the scaling laws for bright galaxies. The key to this procedure is the  relation in the top-right panel of Figure 6. The
relation in the top-right panel of Figure 6. The  values for the dwarfs are direct measurements of the DM, as explained above. We assume that they are correct, so they do not require a shift. The shift in MB required to move the dwarfs on to the straight-line fit to the scaling law for bright galaxies is therefore determined. Similarly, keeping the values of
values for the dwarfs are direct measurements of the DM, as explained above. We assume that they are correct, so they do not require a shift. The shift in MB required to move the dwarfs on to the straight-line fit to the scaling law for bright galaxies is therefore determined. Similarly, keeping the values of  fixed, we determine the shifts between the visible and DM values of
fixed, we determine the shifts between the visible and DM values of  and
and  from the two panels that show the
from the two panels that show the  versus
versus  and the
and the  versus
versus  correlations. These shifts in MB, rc, and σ are then applied to the three remaining panels. If the procedure is valid, then the dwarfs should have shifted consistently to the brighter galaxy correlations in all six panels.
correlations. These shifts in MB, rc, and σ are then applied to the three remaining panels. If the procedure is valid, then the dwarfs should have shifted consistently to the brighter galaxy correlations in all six panels.
The shifted versions of the scaling laws are shown in Figure 7. The derived shift in MB is −4.6 mag for the dSph galaxies and −3.5 mag for the dIm galaxies. These shifts imply that the dwarfs have lost 25–70 times more of their baryons than have the brighter galaxies, consistent with the much larger M/L ratios observed in the dwarfs. Although we describe the shift in MB as a relative loss of baryons by the dwarfs, this is not the whole story. Some or all of the scarcity of baryons in extreme dwarfs could be a result of the reionization of the universe and the subsequent difficulty that tiny halos have in capturing gas (Klypin et al. 1999; Bullock et al. 2000; Cattaneo et al. 2011). Also, dIm galaxies contain H i gas that is not measured by MB; in these, part of the above factor-of-25 shift in luminosity is not due to any baryon "depletion"; rather, up to a factor of ∼10 part of the factor of 25 is due to the fact that some baryons are still in H i gas rather than in stars. In this case, the baryon depletion is only a factor of 2.5.
For the core radius, the adopted shift in  is 0.70 for the dSph galaxies and 0.85 for the dIm galaxies. These shifts give the ratio of the core radius of the DM halo to the core radius of the baryonic distribution (stars or H i). If this is correct, then the baryon distributions are much less extended than the DM distributions in the dwarfs, by factors of about 5–7.
is 0.70 for the dSph galaxies and 0.85 for the dIm galaxies. These shifts give the ratio of the core radius of the DM halo to the core radius of the baryonic distribution (stars or H i). If this is correct, then the baryon distributions are much less extended than the DM distributions in the dwarfs, by factors of about 5–7.
The adopted shift in  is 0.40 for the dSph galaxies and 0.50 for the dIm galaxies. That is, the velocity dispersions of the baryons are about 1/3 of the velocity dispersions of the DM halo particles for these dwarfs. If this is correct, then the potential wells of their DM halos are much deeper than one would infer from their baryonic velocity dispersions. From Table 2, the typical baryonic velocity dispersion of the dwarfs is about 10 km s−1. Therefore, the velocity dispersions of their DM halos are about 30 km s−1. This is similar to the velocity dispersions for the halos of the fainter Sc–Im galaxies in Table 1. We explore this similarity further in Section 8.2.
is 0.40 for the dSph galaxies and 0.50 for the dIm galaxies. That is, the velocity dispersions of the baryons are about 1/3 of the velocity dispersions of the DM halo particles for these dwarfs. If this is correct, then the potential wells of their DM halos are much deeper than one would infer from their baryonic velocity dispersions. From Table 2, the typical baryonic velocity dispersion of the dwarfs is about 10 km s−1. Therefore, the velocity dispersions of their DM halos are about 30 km s−1. This is similar to the velocity dispersions for the halos of the fainter Sc–Im galaxies in Table 1. We explore this similarity further in Section 8.2.
Equations (27) and (28) imply that  i.e., that the central surface densities of the DM halos of Sc–Im galaxies are essentially constant with galaxy luminosity. This is illustrated explicitly in Figure 8. Constant surface density directly implies a Faber–Jackson law of the form MDM ∝ σ4 for the dark halo, where MDM is the DM halo mass and σ is its velocity dispersion (Kormendy & Freeman 2004). The dwarf galaxies are also shown in Figure 8, after applying the increases
i.e., that the central surface densities of the DM halos of Sc–Im galaxies are essentially constant with galaxy luminosity. This is illustrated explicitly in Figure 8. Constant surface density directly implies a Faber–Jackson law of the form MDM ∝ σ4 for the dark halo, where MDM is the DM halo mass and σ is its velocity dispersion (Kormendy & Freeman 2004). The dwarf galaxies are also shown in Figure 8, after applying the increases  for dSph galaxies and
for dSph galaxies and  for dIm galaxies that we use to estimate the true core radii of their DM halos. We see that the central DM halo surface densities for the dwarfs are then very similar to those of the brighter galaxies. This consistency is of interest but provides little independent information, because the core radii of the dwarfs were adjusted to fit on the
for dIm galaxies that we use to estimate the true core radii of their DM halos. We see that the central DM halo surface densities for the dwarfs are then very similar to those of the brighter galaxies. This consistency is of interest but provides little independent information, because the core radii of the dwarfs were adjusted to fit on the  scaling law for the brighter galaxies in Figures 6 and 7.
scaling law for the brighter galaxies in Figures 6 and 7.
The product G × (surface density) is an acceleration: the near-constant surface density of the DM halos over a very large range in MB means that the characteristic acceleration of DM halos is almost the same over this entire range in luminosity.
The conclusion that the surface densities of DM halos are essentially independent of luminosity was first noted by Kormendy & Freeman (2004). It is also seen by Spano et al. (2008), Gentile et al. (2009), Donato et al. (2009), Plana et al. (2010), and Salucci et al. (2012) and, slightly more indirectly, by Walker et al. (2010). Within re of the visible matter rather than within rc of the DM, Napolitano et al. (2010) derive a related result, finding that the mean DM density inside re decreases from giant to dwarf galaxies but is constant for dwarfs over a large range in halo mass.
8. COMPARISON OF THE SCALING RELATIONS FOR VISIBLE GALAXIES AND DM HALOS
8.1. Smaller Dwarf Galaxies Form a Sequence of Decreasing Baryon Content
Figure 9 compares the baryonic and DM surface densities of galaxies as functions of luminosity. It shows quantitatively a conclusion that is well known in the literature: the ratio of baryonic mass to DM mass within the radial extent of the baryons decreases strongly with decreasing galaxy luminosity. Like Kormendy et al. (2009, hereafter KFCB) and Kormendy & Bender (2012), we conclude that at MV ≳ −18, the dwarf spiral, Im, and Sph galaxies in Figures 2–9 form a sequence of decreasing baryon content in smaller galaxies.
In contrast, lower-luminosity bulges and elliptical galaxies have much higher surface densities at or inside the effective radius. If mergers of disks make bulges and if we ignore baryonic pulling corrections, then the ratio of visible to DM surface density increases toward lower bulge luminosity. Like Kormendy (1989), like KFCB—which reviews much additional evidence—and like many other authors, we conclude that bulges and ellipticals form a sequence of increasing dissipation during the formation of smaller galaxies.
For the brighter MV < −18 galaxies of all kinds, the effective density in stars is similar to the DM density at or inside the same radius. For Sc–Im systems, this is at least partly a consequence of using maximum-disk decompositions and of the rotation curve conspiracy (Bahcall & Casertano 1985; van Albada & Sancisi 1986; Sancisi & van Albada 1987), i.e., the observation that rotation curves of giant galaxies are roughly flat and featureless, so the parts of galaxies that are controlled by DM are not easily distinguished from the parts that are controlled by visible matter. The total range of  for the brightest disks is large, ranging from less than 2ρorc to substantially larger than 2ρorc for the DM. Most are sufficiently visible matter dominated to support self-gravitating structure such as bars and spiral density waves. A few are DM dominated; then the arguments of Ostriker & Peebles (1973) apply.
for the brightest disks is large, ranging from less than 2ρorc to substantially larger than 2ρorc for the DM. Most are sufficiently visible matter dominated to support self-gravitating structure such as bars and spiral density waves. A few are DM dominated; then the arguments of Ostriker & Peebles (1973) apply.
There is a caveat. For bulges and ellipticals, the high baryon densities at  may pull gravitationally on DM halos by enough to increase their central densities over the values for Sc–Im galaxies that are shown in Figure 9. But bulges and ellipticals have central projected densities that are more than 3 dex higher than the effective densities shown in Figure 9. The central parts of early-type galaxies are very baryon dominated (see also Cappellari et al. 2013b, 2015; Cappellari 2015, who reach similar conclusions). The central densities of disks are 0.7 dex (for an exponential) higher than the effective densities shown in Figure 9. So even pure disks are moderately dominated by visible matter near their centers. Both results are qualitatively as expected: Visible matter needs to dissipate, sink inside the DM, and become self-gravitating enough to form stars and visible galaxies (e.g., Gunn 1987; Ryden & Gunn 1987). Disks also need to be self-gravitating in order to be unstable to the formation of bars and spiral density waves (ABP). And a great deal of dissipation happens in the wet mergers that make coreless-disky-rotating ellipticals (KFCB): their densities rise above the DM densities by larger amounts at fainter MV.
may pull gravitationally on DM halos by enough to increase their central densities over the values for Sc–Im galaxies that are shown in Figure 9. But bulges and ellipticals have central projected densities that are more than 3 dex higher than the effective densities shown in Figure 9. The central parts of early-type galaxies are very baryon dominated (see also Cappellari et al. 2013b, 2015; Cappellari 2015, who reach similar conclusions). The central densities of disks are 0.7 dex (for an exponential) higher than the effective densities shown in Figure 9. So even pure disks are moderately dominated by visible matter near their centers. Both results are qualitatively as expected: Visible matter needs to dissipate, sink inside the DM, and become self-gravitating enough to form stars and visible galaxies (e.g., Gunn 1987; Ryden & Gunn 1987). Disks also need to be self-gravitating in order to be unstable to the formation of bars and spiral density waves (ABP). And a great deal of dissipation happens in the wet mergers that make coreless-disky-rotating ellipticals (KFCB): their densities rise above the DM densities by larger amounts at fainter MV.
At MV > −18, tinier dwarfs are more DM dominated. By MV ≳ −10, they are almost-dark galaxies with just enough of a frosting of stars so that they can be detected. We conclude the following: (1) The differences between dIm and dSph galaxies in all parameter correlations shown in this paper are small. Whether or not a galaxy retains cold gas and can still form stars in today's universe is a second-order effect. This argues—as Dekel & Silk (1986) emphasized—that the baryon retention sequence seen for the fainter galaxies in Figure 9 is generated primarily by supernova-driven baryon loss or another process (such as a failure to capture baryons after reionization) that has the same effect. (2) We suggest that there exists a large population of tiny halos that are essentially dark—that the discoverable galaxies at MV ≳ −13 represent a smaller and smaller fraction of tinier and tinier halos. This has been suggested as the solution to the problem that the fluctuation spectrum of CDM predicts more dwarfs than are observed in environments like the Local Group (e.g., Klypin et al. 1999; Moore et al. 1999).
8.2. Galaxies Are Dim When Halo Vcirc < 42 ± 4 km s−1
Figure 10 shows one of the most important new results in this paper: the baryon content of galaxies goes to nearly zero robustly at halo Vcirc = 42 ± 4 km s−1. This is another representation of the galaxy baryon retention sequence. The inference is that still-lower-mass halos are mostly dark; they contain a discoverable frosting of baryons only if they manage at least slightly to avoid the physical processes that created the baryon retention sequence.
Figure 10 shows that rotation curve decompositions reveal a linear correlation between the maximum rotation velocities Vcirc,disk of galaxy disks and the outer, circular-orbit rotation velocities Vcirc of massless test particles in their halos. Baryons become unimportant where this extrapolates to Vcirc,disk = 0, i.e., at Vcirc ≃ 42 ± 4 km s−1.
The black and red points in Figure 10 show the maximum rotation velocities given by the rotation curve decompositions for the disk and bulge, respectively. The decompositions results are from van Albada et al. (1985), Athanassoula et al. (1987), Kent (1987, 1989), Carignan & Freeman (1988), Jobin & Carignan (1990), Begeman et al. (1991), Puche & Carignan (1991), Puche et al. (1991), Broeils (1992), Martimbeau et al. (1994), Miller & Rubin (1995), Rhee (1996), Sofue (1996), de Blok & McGaugh (1997), Sicotte & Carignan (1997), van Zee et al. (1997), Verdes-Montenegro et al. (1997), Verheijen (1997), Carignan & Purton (1998), Meurer et al. (1998), Blais-Ouellette et al. (1999), Côté et al. (2000), Swaters et al. (2000), de Blok & Bosma (2002), Corbelli (2003), Weldrake et al. (2003), Chemin et al. (2006), Gentile et al. (2007), Noordermeer et al. (2007), de Blok et al. (2008), Dicaire et al. (2008), Noordermeer (2008), Yoshino & Ichikawa (2008), Sofue et al. (2009), Elson et al. (2010), Puglielli et al. (2010), and Oh et al. (2011a, 2011b).
The disk and bulge fits in Figure 10 are, respectively,


where all quantities are in km s−1. The important result is that both fits robustly have intercepts at Vcirc > 0. Little extrapolation is needed: baryonic disks disappear at Vcirc ≃ 42 ± 4 km s−1. This result is insensitive to the choice of maximum-disk decompositions: Vcirc is much less sensitive to the assumed M/L than are ρo and rc, and in any case, only the high-Vcirc points would be affected if disks were not maximal, because the Vcirc ≃ 50 km s−1 dwarfs are so DM dominated that the choice of M/L scarcely matters. The extrapolation of the black line in Figure 10 to the Vcirc,disk = 0 intercept is so small that this intercept would remain almost unchanged if the slope of the line changed slightly.
It is well known that smaller galaxies are more completely dominated by DM (Figure 9), but Figure 10 provides a measure of the halo mass at which baryons become dynamically unimportant. Dwarf spheroidal and irregular galaxies with M/L values of ∼10–102 (the objects in Table 2) are missing from Figure 10; they do not rotate rapidly enough for rotation curve decomposition. But they are examples of objects with trace amounts of baryons that lie below the black points in Figure 10. The message is that dark galaxies are likely to have Vcirc ≲ 42 ± 4 km s−1 and σ ≲ 30 ± 3 km s−1. These values are remarkably similar to the values that we derive for DM halos of dSph and dIm galaxies from their baryonic velocity dispersions (Section 7). Thus, we conclude that, at the Vcirc where galaxies get dim, their properties are just like the (dim) dSph galaxies in our sample. We regard this Vcirc agreement as a sign that our conclusions are robust.
In fact, Figures 9 and 10 together make a strong case that the sequence of almost-empty halos may extend to smaller Vcirc and σ than the above values. So we again suggest that, at lower luminosities, the galaxies that are plotted are increasingly the "tip of an iceberg" of undiscovered, still-darker dwarfs, as predicted by the CDM density fluctuation spectrum.
Important: these extreme dwarfs apparently remain luminous in the Virgo cluster. There is no "missing dwarfs problem" in the Virgo cluster (Moore et al. 1999). Perhaps the much richer proto-Virgo environment was so dense with jostling, small protogalactic halos and turbulent gas that small halos could capture gas more easily than (say) in the proto Local Group, where there likely was more empty space and where gas ejected from galaxies by supernovae could be thrown farther away from tiny DM halos.
9. CONCLUSIONS
This section discusses our results. The arXiv:1411.2170 preprint of this paper explicitly distinguishes between observational results in black font and theoretical conclusions in blue font.
9.1. Dark Matter Halos Satisfy Well-Defined Scaling Laws
The main observational result of this paper is that DM halos of Sc–Im galaxies satisfy well-defined scaling laws. Halos in less luminous galaxies have smaller core radii, higher central densities, and smaller velocity dispersions. This confirms the results of our previous analyses of smaller samples (Kormendy 1988, 1990; Kormendy & Freeman 1996, 2004). Scaling laws provide new constraints on the nature of DM (e.g., Tremaine & Gunn 1979) and on galaxy formation and evolution. Most of these remain to be explored. Simple implications and other correlation results are summarized in this section.
9.2. Dwarf Spheroidals Are Real Galaxies, Not Tidal Fragments
The surprisingly high DM densities in dwarf spheroidals are normal for galaxies of such low luminosity (Kormendy 1987a). This implies (Kormendy 1988, 1990) that dSph galaxies are real galaxies that collapsed out of the DM fluctuation spectrum. They are not tidal fragments. Tides plausibly can pull bound fragments out of more luminous galaxies, but they cannot retain even the relatively low DM densities in those progenitors (Barnes & Hernquist 1992), much less increase ρ◦ to the high values characteristic of dwarf spheroidals.
Figure 6 shows that the DM halo density of the faintest dwarfs can exceed 1 M⊙ pc−3. This halo density is much higher than the density of the Galactic disk near the Sun (∼0.1 M⊙ pc−3). Although the low surface brightnesses of the faintest dwarfs may make them appear fragile, their high DM densities make them in fact among the most robust to tidal disruption by their parent galaxy. We could expect that accreted faint dwarfs would survive orbital decay and tidal disruption and would end up, possibly intact, in the inner regions of the parent system.
In this context, we can compare the location of the DM-dominated dSph galaxies in the plane of half-light radius rh versus luminosity L with the location of the baryon-dominated globular clusters, non-dwarf spheroidals (sometimes called dwarf ellipticals), and normal, small (i.e., compact) ellipticals (e.g., Kormendy & Bender 2012; Brodie & Romanowsky 2015). The dSph galaxies have rh values that are one to two orders of magnitude larger than the baryon-dominated objects at similar L. Again, this is an indication that the baryons in the dSph systems are a minor tracer component, almost irrelevant to the equilibrium of these galaxies.
9.3. Dwarf Spheroidal, Spiral, and Irregular Galaxies Form a Single Physical Sequence in Their DM Parameters
Dwarf spheroidal galaxies are not included in the least-squares fits in Figure 7 because only ρ◦ can be derived for their halos. However, we show that, with a simple shift in baryonic MB,  and
and  the dwarfs lie on the extrapolation of the DM scaling laws for brighter galaxies in all panels of Figure 7. Section 9.4 interprets the shifts. If it is correct, then DM halos of dSph and Sc–Im galaxies form a single physical sequence as a function of DM core density, velocity dispersion, or—by inference—DM mass.
the dwarfs lie on the extrapolation of the DM scaling laws for brighter galaxies in all panels of Figure 7. Section 9.4 interprets the shifts. If it is correct, then DM halos of dSph and Sc–Im galaxies form a single physical sequence as a function of DM core density, velocity dispersion, or—by inference—DM mass.
9.4. The DM Correlations Provide a Way to Estimate the Baryon Loss and the Dynamical Properties of the DM Halos of Dwarf Galaxies
The central DM densities ρ◦ of dwarf galaxies are, within the approximations of our analysis that ρ(r) ≃ constant, derived correctly, independent of the unknown DM core radius rc and velocity dispersion σ. This provides us with a way to estimate both the baryon loss for these galaxies and the true values of rc and σ for their DM halos:
To shift the dwarf galaxies onto the extrapolation of the  correlation for brighter galaxies, we need to assume that they have or once had enough additional baryons such that, if these were converted into stars, the galaxies would be substantially more luminous. These shifts are ΔMB ≃ −4.6 mag for dSph galaxies and ΔMB ≃ −3.5 mag for dIm galaxies, both relative to brighter galaxies that themselves probably lost a significant fraction of their baryons. To shift the dwarfs onto the other DM correlations then implies that the core radius of the DM is larger than the core radius of the visible matter by
correlation for brighter galaxies, we need to assume that they have or once had enough additional baryons such that, if these were converted into stars, the galaxies would be substantially more luminous. These shifts are ΔMB ≃ −4.6 mag for dSph galaxies and ΔMB ≃ −3.5 mag for dIm galaxies, both relative to brighter galaxies that themselves probably lost a significant fraction of their baryons. To shift the dwarfs onto the other DM correlations then implies that the core radius of the DM is larger than the core radius of the visible matter by  for Sph galaxies and by
for Sph galaxies and by  for dIm galaxies. And the DM particle velocity dispersion is larger than the velocity dispersion of the stars in dSph galaxies by
for dIm galaxies. And the DM particle velocity dispersion is larger than the velocity dispersion of the stars in dSph galaxies by  and larger than the velocity dispersion in the gas in dIm galaxies by
and larger than the velocity dispersion in the gas in dIm galaxies by  With these shifts, dwarfs of both kinds lie on the extrapolation of the DM correlations that we derived for galaxies with rotation curve decomposition in all panels of Figure 7.
With these shifts, dwarfs of both kinds lie on the extrapolation of the DM correlations that we derived for galaxies with rotation curve decomposition in all panels of Figure 7.
The above shifts are consistent with the hypothesis that fainter dwarfs have lower visible matter densities (Figure 9) and higher M/LV ∼ 102–103 because they lost more of their baryons early. One possible reason is galactic winds (e.g., Dekel & Silk 1986). In the absence of DM, the loss of most baryons would unbind the few stars that had already formed. But since faint galaxies have dense DM halos, the systems remain bound despite any baryon loss. An alternative to baryon blowout is the difficulty of capturing or holding on to baryons in low-mass DM potential wells when the universe was reionized (Klypin et al. 1999; Bullock et al. 2000; Cattaneo et al. 2011). In addition, dIm galaxies are relatively dark in part because some of their baryons are still in H i gas.
The inferred shifts of  in dSph galaxies and 0.50 in dIm galaxies imply that these almost-dark dwarfs have higher DM masses than we thought. They imply that the typical velocity dispersions of their DM halos are σ ∼ 30 km s−1. Thus, these galaxies lie near the Vdisk = 0 km s−1 intercept at Vcirc ≃ 42 ± 4 km s−1 of the black line in Figure 10. It is not clear that we have discovered any galaxies with DM
in dSph galaxies and 0.50 in dIm galaxies imply that these almost-dark dwarfs have higher DM masses than we thought. They imply that the typical velocity dispersions of their DM halos are σ ∼ 30 km s−1. Thus, these galaxies lie near the Vdisk = 0 km s−1 intercept at Vcirc ≃ 42 ± 4 km s−1 of the black line in Figure 10. It is not clear that we have discovered any galaxies with DM  km s−1.
km s−1.
9.5. Spiral, Irregular, and Spheroidal Galaxies with MV ≳ −18 Form a Sequence of Decreasing Baryon-to-DM Ratio at Decreasing Luminosity
Figure 9 robustly illustrates the well-known result that the ratio of baryon surface density to DM surface density decreases dramatically at MV ≳ −18. By MV ∼ −10, galaxies typically have M/LV ∼ 102. The most extreme dwarfs barely contain enough baryons to be discoverable. Specifically, Figure 10 shows that the baryon content of spiral and irregular galaxies goes to zero at DM halo Vcirc > 0. Instead, the Vcirc,disk = 0 km s−1 intercept of the remarkably linear and very well determined correlation of the black points in Figure 10 happens at halo Vcirc = 42 ± 4 km s−1. Smaller galaxies are robustly faint. In Section 9.4, we suggest that fainter dSph and dIm galaxies form a sequence of decreasing baryon retention or capture in tinier galaxies. Note again that some "apparently missing" baryons in dIm galaxies are present in H i gas.
As the DM  decreases in Figure 10, bulges get less massive more rapidly than disks. Bulges disappear entirely at Vcirc ∼ 104 ± 16 km s−1. This is consistent with the well-known observation that galaxies such as M33 usually do not have bulges. Much fainter galaxies never have bulges. At high Vcirc, we note that there exist bulgeless galaxies at all Vcirc up to at least 300 km s−1 (see Kormendy et al. 2010 and Fisher & Drory 2011 for statistics).
decreases in Figure 10, bulges get less massive more rapidly than disks. Bulges disappear entirely at Vcirc ∼ 104 ± 16 km s−1. This is consistent with the well-known observation that galaxies such as M33 usually do not have bulges. Much fainter galaxies never have bulges. At high Vcirc, we note that there exist bulgeless galaxies at all Vcirc up to at least 300 km s−1 (see Kormendy et al. 2010 and Fisher & Drory 2011 for statistics).
9.6. Differences Between S+Im Galaxies and Sph Galaxies Are a Relatively Minor, Second-Order Effect
The differences between S+Im galaxies (blue points in Figure 9) and Sph galaxies (green points in Figure 9) are small. In particular, both galaxy kinds have similarly decreasing baryon-to-DM density and mass ratios at lower galaxy luminosities. And among extreme dwarfs, some dSphs contain no gas and no young stars; other dSphs contain no gas but formed stars relatively recently, and dIm galaxies such as M81 dwarf A contain modest amounts of gas and still form stars gently. But all of these galaxies have similar structure (Figure 5 and
This circumstance extends to higher galaxy masses, too: Kormendy & Bender (2012) show that Sph galaxies are essentially bulgeless S0 galaxies, that S0 disks extend the Sph correlations to higher luminosities, and that S0 disks and spiral galaxy disks also have similar structural parameter correlations. Like Kormendy & Bender (2012) and more explicitly Kormendy (2015), we conclude that the differences between z ∼ 0 galaxies that still contain gas (and that still can form stars) and those that do not (and that can not) are relatively minor.
This is consistent with the general picture advocated in papers like Dekel & Silk (1986) and Kormendy & Bender (2012) that the most important physical processes (probably more than one) that control the formation of dwarf galaxies are the ones that determine the baryon depletion. Whether all or just most of the cold gas gets ejected, gets used up, or never gets accreted is secondary.
It is interesting to note that almost all galaxies detected in the HIPASS blind H i survey for galaxies with velocities ≲12,000 km s−1 were also detected in starlight. Galaxies with H i gas and DM but no stars appear to be very rare in the nearby universe (Doyle et al. 2005).
9.7. There May Exist a Large Population of Dwarf Galaxies That Are Completely Dark
We suggested in our earlier papers (Freeman 1987; Kormendy 1988, 1990; Kormendy & Freeman 2004) that there may exist a large population of galaxies that are completely dark. This was based on the observation that, as luminosity decreases, dwarf galaxies become much more numerous and much more nearly dominated by DM. Similar suggestions were made for different reasons by Tully et al. (2002).
This hypothesis is greatly strengthened by Figure 10. Rotation curve decompositions reveal a linear correlation between the maximum rotation velocities Vcirc,disk of galaxy disks and the outer, circular-orbit rotation velocities Vcirc in their halos. It extrapolates to Vcirc,disk = 0 (i.e., baryons become unimportant) at Vcirc ∼ 42 km s−1. In Section 7, we conclude that dSph galaxies also live in halos with Vcirc ≃ 42 km s−1. This means that the range of baryon content of such DM halos is very large, extending from galaxies that allow rotation curve decomposition to extreme dwarfs that can only be found by detecting tiny enhancements in star counts.
Our results suggest that empty halos are likely to be darker versions of Draco, UMi, and the ultrafaint dSph galaxies. DM halos that contain H i gas but no stars are rarely detected. Tiny dSph galaxies have only a frosting of baryons because they lost or never captured more. But there is nothing magic about owning a few percent of the normal baryon content. Draco and UMi do not know or care that they contain just enough baryons to be discovered by us 12 billion years after they formed. If many DM halos captured or kept even fewer baryons, they could escape detection and form a population of dark dwarfs.
Undiscovered dark dwarfs could solve the problem that the spectrum of initial density fluctuations predicted by CDM predicts too many dwarf satellites of giant galaxies (Klypin et al. 1999; Moore et al. 1999; Bullock et al. 2000; Simon & Geha 2007; Diemand et al. 2008; Diemand & Moore 2011; Kirby et al. 2008; Springel et al. 2008; Tollerud et al. 2008; Bovill & Ricotti 2009, 2011a, 2011b; Walsh et al. 2009). The favored explanation for why these dwarfs are not seen is that they virialized early, before or during the reionization of the universe, and so lost or never captured the canonical fraction of baryons because the baryons were too hot to be confined in shallow DM potential wells.
Our suggestion is borne out by the discovery of ultrafaint dwarfs with MB as faint as −1 (see Simon & Geha 2007; Tolstoy et al. 2009 for reviews and Table 2 for references on galaxies used here). Large surveys such as the Sloan Digital Sky Survey (York et al. 2000) have made it possible to detect ever-darker dwarfs via ever-smaller star-count excesses. The DM densities of these galaxies are in the range seen for brighter dSph galaxies and for the smallest galaxies with rotation curve decompositions. They are real galaxies in the sense of Section 9.2. They are darker than Draco and UMi. And they hint that still-darker galaxies probably exist.
We emphasize that there is no sign of any discontinuity in baryon fractions as a function of galaxy mass. Only the names that we give to galaxy types change as baryon fractions decrease. The largest baryon fractions belong to spiral galaxies whose baryons are self-gravitating enough to dissipate into disks and to make internal structures such as bars and spiral arms. Medium-large baryon depletions can apply to either dSph or dIm galaxies, depending on their environments. These include galaxies that still have gas but that have low enough baryon content so that the baryons have not organized themselves into disks. In these dIm galaxies, some of the factor-of-25 apparent "baryon depletion" (up to a factor of 10) is not due to low baryon content but rather is due to the fact that the baryons are still in gas. That is, in various dIm galaxies with various H i/stellar mass fractions, the true baryon depletion factor ranges from ∼25 (in galaxies with little H i) to ∼2.5 (in galaxies with H i/stellar mass ratios of ∼10). More extreme galaxy environments are so hostile to dwarfs that they cannot retain gas; then we call them dSph galaxies and necessarily measure even larger baryon depletions. And then all of the apparent baryon depletion is associated with baryon absence, not baryon "hiding" in H i gas. At all small DM masses, there is a large range in baryon depletions. There is substantial overlap in MB between spiral galaxies, Im or dIm galaxies, and Sph or dSph galaxies. It is likely that there is overlap in DM mass between each of the above groups and dark galaxies. We see no reason to postulate a dichotomy in baryon properties at any DM mass.
9.8. Not Too Big To Fail (TBTF)
S. Faber (2015, private communication) points out that our results suggest at least a partial solution to another problem with ΛCDM galaxy formation, TBTF. It is closely related to the problem that the spectrum of initial density fluctuations predicts more halo substructure than we observe in dwarf galaxy companions of (e.g.) our Galaxy or M31. For the smallest and most numerous such halos, the solution may be that they never formed visible galaxies (Section 9.7). But many authors (e.g., Boylan-Kolchin et al. 2011, 2012; Garrison-Kimmel et al. 2013, 2014) have pointed out that intermediate-mass halos with Vcirc ∼ 30–70 km s−1 (i.e., galaxies that are a little less massive than the Magellanic Clouds) are TBTF in that they are too massive to fail to accrete or to hold on to discoverable masses of baryons. Whether this problem is or is not new and separate from other dwarf galaxy formation problems depends in part on whether or not these dwarfs have cored or cuspy (i.e., NFW) density profiles (see Garrison-Kimmel et al. 2013, 2014).
We conclude (Section 9.4) that dSph and dIm galaxies whose stellar and gas velocity dispersions are σ ∼ 10 km s−1 really live in bigger halos with σ ∼ 101.5 km s−1 and Vcirc ∼ 42 km s−1. This is probably an underestimate. Our  estimate was based on an extrapolation of correlations that, at the low-mass end, include galaxies that are dominated by DM and that have M/L values of ∼101. These objects (e.g., DDO 154; Carignan & Freeman 1988) almost certainly also lost baryons. If we could correct for this loss, then these galaxies would be plotted at brighter MB and the derived DM parameter correlations would get slightly steeper. We would derive a slightly larger value of
estimate was based on an extrapolation of correlations that, at the low-mass end, include galaxies that are dominated by DM and that have M/L values of ∼101. These objects (e.g., DDO 154; Carignan & Freeman 1988) almost certainly also lost baryons. If we could correct for this loss, then these galaxies would be plotted at brighter MB and the derived DM parameter correlations would get slightly steeper. We would derive a slightly larger value of  This correction cannot be made too large or the total masses of these dwarfs become uncomfortable large. But if
This correction cannot be made too large or the total masses of these dwarfs become uncomfortable large. But if  –0.6, then the larger dSph and dIm galaxies in our sample are in the mass range of the TBTF "missing galaxies." Therefore, we suggest that the solution to the TBTF problem is at least in part that intermediate-mass dwarfs are present in the Local Group but are masquerading as smaller galaxies. Brook & Di Cintio (2015) reach a similar conclusion via a different route.
–0.6, then the larger dSph and dIm galaxies in our sample are in the mass range of the TBTF "missing galaxies." Therefore, we suggest that the solution to the TBTF problem is at least in part that intermediate-mass dwarfs are present in the Local Group but are masquerading as smaller galaxies. Brook & Di Cintio (2015) reach a similar conclusion via a different route.
9.9. Dwarf Spheroidal Galaxies Formed Δzcoll ≳ 10 Earlier than Spiral and Irregular Galaxies
Virialized DM density depends on collapse redshift zcoll,  The DM densities for classical dSph galaxies like Draco and UMi are about 100 times higher than those for the brightest spirals. The collapse redshifts of the halos of Draco and UMi and those of the brightest spiral galaxies are then related by
The DM densities for classical dSph galaxies like Draco and UMi are about 100 times higher than those for the brightest spirals. The collapse redshifts of the halos of Draco and UMi and those of the brightest spiral galaxies are then related by  . For the faintest dSph galaxies, this ratio is about 8. If there is a correction for baryonic DM compression in the giant galaxies, then it would make their DM ρ◦ smaller, and this would increase the above ratios still further.
. For the faintest dSph galaxies, this ratio is about 8. If there is a correction for baryonic DM compression in the giant galaxies, then it would make their DM ρ◦ smaller, and this would increase the above ratios still further.
9.10. The Power Spectrum of Initial Density Fluctuations
Djorgovski (1992) compared an earlier version of the DM parameter correlations to the scaling laws predicted by hierarchical clustering (Peebles 1974; Gott & Rees 1975). For a power spectrum of initial density fluctuations that is a power law in wavenumber k,  the size R, density ρ, and velocity dispersion σ of a bound object are related approximately by
the size R, density ρ, and velocity dispersion σ of a bound object are related approximately by



Here we have used the relation  for an ITS. Djorgovski pointed out that the DM parameter correlations in Kormendy (1990) imply that n ≃ −2.45, close to the value n ≃ −2 expected for giant galaxies in CDM theory. The more accurate fits in Equations (31)–(33),
for an ITS. Djorgovski pointed out that the DM parameter correlations in Kormendy (1990) imply that n ≃ −2.45, close to the value n ≃ −2 expected for giant galaxies in CDM theory. The more accurate fits in Equations (31)–(33),



give n = −1.83 ± 0.17, n = −2.07 ± 0.07, n = −2.08 ± 0.17, respectively. These values are not independent. Their average, n = −2.0 ± 0.1, is significantly improved over earlier determinations. It is remarkably close to the value n ≃ −2.1 expected in ΛCDM theory at a halo mass of 1012 M⊙ (Shapiro & Iliev 2002). Note that the slopes have not been corrected for baryonic DM compression. The above comparison provides a measure of the slope of the fluctuation power spectrum on mass scales that are smaller than those accessible to most other methods.
Shapiro & Iliev (2002) have made a more detailed comparison of the DM parameter correlations published by Kormendy & Freeman (1996) with their predictions based on COBE-normalized CDM fluctuation spectra. They found that the agreement between predictions and observations is best for ΛCDM.
It is interesting to note a consequence of the theoretical prediction that the slope n gets steeper at smaller mass scales. If n ≃ −2.6 for the smallest dwarfs (Shapiro & Iliev 2002; Ricotti 2003), then the straight lines in the left panels of Figure 6 should curve downward toward the visible matter parameters of dSph galaxies. It will be important to look for curvature in the correlations as more data become available for dwarf galaxies.
9.11. Could Galaxy Disks Be Very Submaximal?
Some authors (e.g., van der Kruit 2010) have suggested that late-type galaxy disks are very submaximal, with M/L of ∼0.5–0.7 of maximum-disk values. We addressed this issue in Section 2.2. Here, having derived DM correlations based on maximum-disk decompositions, we can use these results to help justify our assumptions "after the fact," as follows:
If the disks of giant spirals (MB < −19) are typically 2/3 maximal, then DM core radii must be decreased and DM central densities must be increased to maintain good fits to the rotation curves. The inevitable consequence is that ρ◦ for the biggest galaxies becomes almost as big as the values for dwarf galaxies that we illustrate in Figure 6. That is, the  correlation would get very shallow, with only a small range in ρ◦. This has three uncomfortable or even untenable consequences:
correlation would get very shallow, with only a small range in ρ◦. This has three uncomfortable or even untenable consequences:
1. The derived differences in the formation redshifts of giant and dwarf galaxies would get much smaller than the current values in Section 9.9. This would be inconsistent with current thinking that the smallest known dwarfs formed (i.e., their halos collapsed and virialized) at z ≳ 10.
2. Our derived ∣ΔMB∣ of baryon loss would get much smaller:  The inferred baryon deficiency would then be too small to be consistent with the large M/L ratios of ∼102 that are almost universally measured for these dwarfs.
The inferred baryon deficiency would then be too small to be consistent with the large M/L ratios of ∼102 that are almost universally measured for these dwarfs.
3. Shallower DM parameter correlations would force us to derive a slope of the power spectrum of initial density fluctuations (Section 9.10) that is very different from −2. That derivation is an important consistency check that nothing has gone very wrong with our derivation of the parameter correlations. If DM halos are so cuspy that our analysis is invalid, or if disks are so submaximal that our derivations of the correlation slopes are very wrong, then the Section 9.10 consistency with the slope of the ΛCDM fluctuation spectrum vanishes. The success of the comparison in Section 9.10 is an argument in favor of our assumptions. This includes our omission of any corrections to the correlation slopes that result from taking account of the compression of DM halos in giant galaxies that is caused by the gravity of their baryons.
9.12. Caveats and Future Work
We emphasize that the scatter in Figures 2–4 and 6–8 has surely been increased by problems with the data.
1. Distance errors are smaller than in previous derivations of the correlations, but they are not negligible.
2. The Table 1 parameters are very heterogeneous. Inconsistencies in rotation curve decomposition procedures used by different authors inflate the scatter. For example, the Broeils (1992) galaxies define the same correlations with fewer points but smaller scatter than the sample as a whole.
3. If some disks are submaximal, then this affects the scatter in the correlations. If the degree to which they are submaximal depends on MB (Kranz et al. 2003; Bosma 2004; van der Kruit & Freeman 2011), then this also affects the correlation slopes.
4. The assumption that DM halos have isothermal cores is challenged by CDM theory, although it is suppported by many observations. It will be important to see how the correlations are affected if NFW or Einasto halos are used.
5. DM compression by the visible matter (Sellwood & McGaugh 2005) may affect some galaxies more than others. ABP found early versions of the present DM correlations; even in their small sample, they already observed that many early-type galaxies deviate toward small rc and large ρ◦ compared to the DM correlations for late-type galaxies. They interpreted this as a result of the compression of DM halos by the gravity of the visible components. Similar deviations were similarly interpreted by Kormendy (1988, 1990), Thomas et al. (2009), Thomas (2010), Jardel et al. (2011), and Bender et al. (2015). Correction for baryonic compression of DM likely would decrease the measured ρo values slightly for giant but not dwarf galaxies. This would increase the difference between low ρo values in giant galaxies and high ρo values in dwarf galaxies.
If disks are submaximal and if their gravity compresses DM, then the corrections for these effects change ρo in opposite directions. It is possible that these corrections are modestly significant but fortuitously cancel.
6. We have consistently used the absolute magnitude MB as a measure of baryonic mass against which to scale the DM halo parameters. For some of the fainter dIm galaxies, the baryonic mass is dominated by the H i mass, and it would make sense to use a total baryonic mass as is done in deriving the baryonic Tully–Fisher relation. This affects our interpretation of the ΔMB shift for some dIm galaxies in Figure 7 as discussed in Section 7. We are grateful to J. S. Gallagher and to the referee for this suggestion.
7. In selecting dIm galaxies for this sample, we were probably overcautious in choosing galaxies that have small solid-body rotation. The Gaussian surface density and related apparatus for estimating the core density of the DM halo core are expected to work for regions of these galaxies in which the rotation is solid body.
We also acknowledge that the shifts ΔMB,  and
and  determined in Section 7 and discussed further in Section 9.4 are probably underestimated. The smallest dS + dIm galaxies that have rotation curve decomposition results in Table 1, in Figures 2–4, and in the correlation derivations in Equations (21)–(33) have mass-to-light ratios of M/LV ∼ 101. Consistent with the rest of our discussion, they probably also have lost a substantial fraction of their baryons. Certainly they are faint enough to be on the baryon depletion sequence illustrated in Figure 9. If we could correct for this baryon loss, then the correlations that we derive would get steeper. Consequently, all parameter shifts for the extreme dSph and dIm galaxies would get somewhat larger. None of our conclusions would change qualitatively, but correlations and shifts both would get tweaked. We would infer that the smallest detected DM halos have particle velocity dispersions that are slightly bigger than σ ∼ 30 km s−1.
determined in Section 7 and discussed further in Section 9.4 are probably underestimated. The smallest dS + dIm galaxies that have rotation curve decomposition results in Table 1, in Figures 2–4, and in the correlation derivations in Equations (21)–(33) have mass-to-light ratios of M/LV ∼ 101. Consistent with the rest of our discussion, they probably also have lost a substantial fraction of their baryons. Certainly they are faint enough to be on the baryon depletion sequence illustrated in Figure 9. If we could correct for this baryon loss, then the correlations that we derive would get steeper. Consequently, all parameter shifts for the extreme dSph and dIm galaxies would get somewhat larger. None of our conclusions would change qualitatively, but correlations and shifts both would get tweaked. We would infer that the smallest detected DM halos have particle velocity dispersions that are slightly bigger than σ ∼ 30 km s−1.
We will address these issues in future papers.
This work has been in progress for many years; we owe our warm and sincere thanks to many people for their help and support. J.K. is grateful to the Directors and staff of Mt. Stromlo Observatory for their hospitality during four visits when parts of this work were done. J.K. also thanks the Alexander von Humboldt-Stiftung (Germany) for the Research Award that made possible his early visits to the Universitäts-Sternwarte, Ludwig-Maximilians-Universität, Munich, where other parts of this work were done. More recently, J.K. has visited the Max-Planck-Institut für Extraterrestrische Physik (MPE) as an External Member. The hospitality of the Sternwarte, the MPE, and its Directors, R. Bender, R.-P. Kudritzki, and R. Genzel, is much appreciated. We thank S. Djorgovski, S. M. Faber, S. M. Fall, J. S. Gallagher, and P. Shapiro for helpful discussions. We are grateful to the referee for a very thorough reading that led to significant improvements in the text. We also thank R. Bender for making available the program (Kormendy & Bender 2009) that was used to construct the symmetric least-squares fits. Finally, J.K. warmly acknowledges the productive collaboration with A. Bosma on DDO 127, whose results in Table 1 are quoted from Kormendy & Freeman (2004).
K.C.F. is grateful to the Aspen Physics Center (NSF grant #1066293) and the MPE and the European Southern Observatory for hospitality on several occasions during which parts of this work were done.
This work would not have been practical without extensive use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory and the California Institute of Technology under contract with NASA. We also used the HyperLeda database, http://leda.univ-lyon1.fr (Paturel et al. 2003). Finally, we made extensive use of NASA's Astrophysics Data System bibliographic services.
K.C.F.'s recent work on dark matter was supported by ARC grant DP150104129.
J.K.'s work on this subject was supported by NSF grants AST-9219221 and AST-0607490, by the Alexander von Humboldt-Stiftung, and by Sonderforschungsbereich 375 of the German Science Foundation. The visits to Mt. Stromlo were made possible by the long-term support provided to J.K. by the Curtis T. Vaughan, Jr. Centennial Chair in Astronomy. We are most sincerely grateful to Mr. and Mrs. Curtis T. Vaughan, Jr. for their support of Texas astronomy.