NUSTAR, SWIFT, AND GROND OBSERVATIONS OF THE FLARING MEV BLAZAR PMN J0641−0320

Blazars are an extreme class of active galactic nuclei (AGNs) whose bright and violently variable panchromatic emission is ascribed to the presence of a collimated relativistic jet closely aligned to our line of sight (e.g., Blandford & Rees 1978). These objects are typically hosted in the nuclei of giant elliptical galaxies (Falomo et al. 2000; O'Dowd et al. 2002) and can be powered by accretion onto larger-than-average super-massive black holes (see e.g., Ghisellini et al. 2010; Shaw et al. 2013). Blazars are sub-classified into flat-spectrum radio quasars (FSRQs) and BL Lacertae (BL Lac) objects depending on the presence (or absence for BL Lacs) of emission lines in their optical spectra with rest-frame equivalent widths >5 Å (e.g., Urry & Padovani 1995; Marcha et al. 1996).

Among all blazars, the so-called "MeV blazars" those having an inverse Compton peak located in the MeV band (Bloemen et al. 1995; Sikora et al. 2002; Sambruna et al. 2006), may be the most extreme objects. These rare, extremely luminous objects are mostly found at high ($z\gt 2\mbox{--}3$) redshift and are thought to host super-massive black holes with masses often in excess of 10⁹ M${}_{\odot }$ (e.g., Ghisellini et al. 2010). Since each detected blazar implies the presence¹⁷ of a much larger population of objects with jets pointing somewhere else, the few detections of these extreme blazars are instrumental to set constraints on the mass function of heavy black holes. This becomes particularly important at redshift $z\gt 4$ when the age of the universe is barely compatible with the time needed to grow such monstrous black holes exclusively by accretion (Volonteri et al. 2011; Ghisellini et al. 2013). All this has sparked a renewed interest in this elusive, yet interesting, class of blazars.

Lacking an MeV all-sky instrument, the most efficient domain in which to detect MeV blazars is the hard X-ray (>10 keV) band. In this energy range, such objects display remarkably hard spectra, which easily distinguish them from other, more normal, sources. The Swift Burst Alert Telescope (BAT) survey detected 26 FSRQs of which ∼40% are at z >2 (Ajello et al. 2009) and host massive black holes (Ghisellini et al. 2010). This is in contrast to Fermi-LAT, which has detected >400 FSRQs, but only ∼12% of those are located at $z\gt 2$ (Ackermann et al. 2015). This is mostly due to the fact that high-redshift FSRQs are soft γ-ray sources (e.g., power-law photon indices >2.4–2.5) and since the LAT point-spread function (PSF) increases at low energies, it is hard to disentangle point-source emission from the bright diffuse Galactic emission.

In the absence of an all-sky hard X-ray survey more sensitive than the one obtained with Swift/BAT, MeV blazar candidates have recently been identified on the basis of radio, IR, optical, and soft X-ray observations (e.g., Sbarrato et al. 2012; Ghisellini et al. 2014a) and then later confirmed by NuSTAR hard X-ray observations (Sbarrato et al. 2013). Another strategy relies on the detection and identification of MeV blazars during flaring episodes at γ-rays. Here we report on the Fermi detection of the transient source Fermi J0641−0317 (Kocevski et al. 2014) later identified to be coincident with the radio source PMN J0641−0320 (Ajello et al. 2014). Because of its potentially interesting nature, we initiated a multi-wavelength campaign and here we present the results of the target of opportunity (ToO) observations carried out by Swift and NuSTAR in X-rays, and with GROND¹⁸ , in the optical/NIR, that firmly establishes PMN J0641−0320 as a new member of the MeV blazar family.

2.1. Fermi

Fermi J0641−0317 was detected as a significant (>6σ) γ-ray transient during the week of 2014 April 14–21 (and reported to the community in an Astronomer's Telegram, Kocevski et al. 2014) by the Fermi all-sky variability analysis (FAVA, Ackermann et al. 2013). FAVA¹⁹ is a real-time analysis that searches the γ-ray sky for weekly transients and detects significant deviations above the mission-averaged flux at every position in the sky. FAVA is an efficient tool to detect weekly transients all over the sky. Figure 1 reports the FAVA light curve of Fermi J0641−0317 with the >6σ flaring episode detected around MJD 56800.

Zoom In Zoom Out Reset image size

Using the standard Fermi science tools²⁰ and P7SOURCE photons, the position of Fermi J0641–0317 was reported to be (for 2014 April 14–21 week, see Kocevski et al. 2014) at R.A. = 100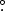383, decl. = –3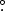294 (J2000) with a 95% confidence region of 0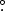25. This source is located in the plane of the Galaxy ($b=-3.703$), but toward the anti-center region. Its γ-ray spectrum, covering the period 2014 April 14–21 and modeled with a power law, exhibited a 0.1–300 GeV flux of $(7.7\pm 1.3)\times {10}^{-7}$ ph cm⁻² s⁻¹ and a photon index of 2.66 ± 0.15. For comparison, less than 10% of the Fermi-LAT detected FSRQs have a larger photon index (Ackermann et al. 2011). Thus, even during the flare, Fermi J0641−0317 displayed a very soft γ-ray spectrum.

A source coincident with Fermi J0641−0317 was later reported (as 3FGL J0641.8−0319) in the 3FGL catalog (Acero et al. 2015) based on four years of Fermi-LAT observations. Its >100 MeV flux averaged over four years was ($1.7\pm 0.5)\times {10}^{-8}$ ph cm⁻² s⁻¹, about 45 times fainter than during the flare. The power-law photon index was 2.45 ± 0.13, similar (within the uncertainties) to the slope during the flare. The long-term FAVA light curve confirms that the source had, over the course of Fermi-LAT observations, a total of two flaring episodes: between 2014 January 1 and 2014 July 4 and between 2015 February 27 and 2015 April 24 (see Figure 1). Here we take advantage of the newly delivered Pass 8 data set to re-analyze the data from Fermi J0641−0317. We use P8_SOURCE photons, the P8R2_SOURCE_V6 instrument response function, and rely on version 10-00-04 of the Fermi science tools. The analysis was performed, following the recommendation²¹ for the analysis of a point source in the plane of the Galaxy, in a region of interest (ROI) centered on the source and with a radius of 15°. All photons detected at zenith angles larger than 90° were removed. The background model comprised the diffuse Galactic and isotropic emission and all 3FGL sources (Acero et al. 2015) within 20° of the source. The spectral parameters of all the sources present within the ROI were left free to vary during the likelihood fitting.

During both long-term flares the source is well detected (with a test statistic, TS,²² of 1591 and 471, respectively) and with similar spectral parameters (see Table 1). The weekly light curves for both flares (reported in Figure 2) show that the source was significantly detected by LAT, with several flaring episodes approaching fluxes (>100 MeV) of 10⁻⁶ ph cm⁻² s⁻¹ accompanied, during those times, by a slightly harder than average spectrum. Figure 2 shows that FAVA first detected the source during the main flare and that the source was still bright during the NuSTAR observation. However, the source reached its maximum two weeks later (on 2014 May 13), reaching a flux of $(1.44\pm 0.13)\times {10}^{-6}$ ph cm⁻² s⁻¹ with a power-law photon index of 2.60 ± 0.10.

Zoom In Zoom Out Reset image size

Table 1.  Table of Observations and Spectral Parameters

Instrument	Datea	Energy Band	Fluxb	Photon Indexc	Description
LAT	Apr 14–Apr 21	0.1–500 GeV	(7.7 ± 1.3)×10−7	2.66 ± 0.15	LAT First detection
LATd	Apr 24–May 01	0.1–500 GeV	(8.2 ± 0.1)×10−7	2.68 ± 0.15	NuSTAR observation
LAT	Jan 17–Jul 04	0.1–500 GeV	(5.9 ± 0.2)×10−7	2.79 ± 0.03	Flare A
LAT	(2015) Feb 27–Apr 24	0.1–500 GeV	(5.5 ± 0.1)×10−7	2.80 ± 0.03	Flare B
XRT	Apr 24	2–10 keV	${4.9}_{-0.5}^{+1.0}\times {10}^{-12}$	${0.93}_{-0.39}^{+0.43}$	⋯
XRT	Apr 26	2–10 keV	${6.2}_{-1.3}^{+0.9}\times {10}^{-12}$	${0.87}_{-0.35}^{+0.43}$	⋯
XRTd	Apr 29	2–10 keV	${7.2}_{-1.3}^{+0.9}\times {10}^{-12}$	${0.93}_{-0.30}^{+0.33}$	⋯
NuSTARd	Apr 29	3–70 keV	$5.2\pm 0.3\times {10}^{-12}$	1.08 ± 0.03	⋯
XRT+NuSTARe	Apr 29	1–70 keV	8.9$\,\pm \,0.2\times {10}^{-12}$	1.06 ± 0.03	⋯

Notes.

^aAll dates of observations are in 2014 unless otherwise noted. ^bFermi-LAT fluxes are in ph cm⁻² s⁻¹; Swift-XRT and NuSTAR fluxes are in erg cm⁻² s⁻¹. ^cPhoton index of the power-law model fitted to the data. ^dData used for building the simultaneous SED reported in Figure 6. ^eThese are the results of the joint fit to XRT and NuSTAR data for the simultaneous observations on April 29.

Download table as:  ASCIITypeset image

2.2. Swift Observations

Swift was triggered to perform three observations: on 2014 April 24, 26, and 29; the last one happened simultaneously with the NuSTAR observation (see Section 2.3). In all three epochs, only one bright source was detected by the X-ray telescope (XRT) within the error region of LAT. The source was localized to R.A. = 6^h41^m51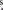20, decl. = –3:20:46.34 (J2000) with a 90% uncertainty of 3.7 arcsec. Figure 3 shows the Fermi-LAT and Swift/XRT localizations. In all observations the source remained very bright with a 2–10 keV flux of $\gtrsim 5\times {10}^{-12}$ erg cm⁻² s⁻¹ and displayed a very hard spectrum with a photon index of ∼1.0. As can be seen in Table 1, in the Swift/XRT observations, there is marginal ($\leqslant 2\sigma$) evidence for variability from one pointing to another, at the level of ∼40%. The source flux extrapolated to the 15–150 keV band is ∼10⁻¹⁰ erg cm⁻² s⁻¹, which would make it easily detectable by Swift/BAT in less than 10⁵ s (see e.g., Ajello et al. 2008; Tueller et al. 2008). The lack of such a source in the most recent BAT catalogs that rely on >50 months of exposure (Cusumano et al. 2010; Ajello et al. 2012; Baumgartner et al. 2013) testifies that this might be an unusually high/hard X-ray state for this source.

Zoom In Zoom Out Reset image size

The prominent flat-spectrum radio source PMN J0641−0320 (Fomalont et al. 2003) lies only 2.4 arcsec away from the XRT centroid and well within its error radius. The source was resolved in prior very long baseline array (VLBA) observations at 8.6 GHz, showing milliarcsecond-scale emission and a total flux of 0.83 Jy. The radio brightness and the small angular separation between XRT and the radio source make the probability that the radio source is a background unrelated object negligible (Petrov et al. 2013). Moreover, within the error box of XRT and compatible with the radio position of PMN J0641−0320 there is a source detected at mid-infrared wavelengths by WISE (J064151.12-032048.4, Wright et al. 2010) with IR colors typical of blazars (Massaro et al. 2011; D'Abrusco et al. 2012, 2014). The source also has a flat spectrum below 1 GHz, which is typical for γ-ray detected blazars (Massaro et al. 2013a, 2013b). We thus consider the association of the blazar-like source PMN J0641−0320 to the transient Fermi J0641−0317 very robust.

2.3. NuSTAR Observations

PMN J0641−0320 was observed with NuSTAR (Harrison et al. 2013) starting at UT 10:01 on 2014 April 29 (MJD 56776). The target was observed for 11 hr, resulting in 21.4 ks of source exposure after event filtering. Data were processed using the NuSTAR Data Analysis Software (NuSTARDAS; Perri et al. 2013) v.1.2.1, and response files from v.2013090 of the Calibration Database. We extracted the NuSTAR source and background spectra from filtered event files using the standard nuproducts script. For the source we used circular extraction regions with a diameter of 60'' for both focal plane modules (referred to as FPMA and FPMB). The background was extracted from large annular regions centered on the source. The choice of extraction region size optimizes the signal-to-noise ratio at high energies; we have verified that alternative choices do not affect any of the results. Due to the very hard spectrum, the target is well detected up to the high-energy end of the NuSTAR bandpass at ∼70 keV. No variability is apparent within the NuSTAR observation.

For spectral modeling, we bin the NuSTAR spectra to a minimum of 20 counts per bin. We use Xspec v. 12.8.1 (Arnaud 1996), and a simple power-law model ${dN}/{dE}\propto {E}^{-{{\rm{\Gamma }}}_{X}}$ for the photon spectrum. The neutral hydrogen column density in the direction of PMN J0641−0320 of 6 × 10²¹ cm⁻² (Kalberla et al. 2005) is too low to significantly attenuate the spectrum above 3 keV, but we include a fixed absorption factor for completeness. The best fit is obtained for a very hard photon index ${{\rm{\Gamma }}}_{X}=1.08\pm 0.03$ (90% confidence interval), with no structure apparent in the residuals and ${\chi }^{2}=285$ for 275 degrees of freedom. The cross-normalization constant between FPMA and FPMB was left free to vary in the fit and found to be 1.02 ± 0.04, consistent with expectations from calibration observations (Madsen et al. 2015). The flux calculated from the power-law model is $(6.8\pm 0.2)\times {10}^{-12}$ erg s⁻¹ cm⁻² for the 2–10 keV energy band and $(4.5\pm 0.2)\times {10}^{-12}$ erg s⁻¹ cm⁻² for the 10–70 keV band. We place an upper limit on the curvature within the NuSTAR bandpass by fitting a log-parabolic model (Tramacere et al. 2007) with one additional parameter ($f(E)\propto {E}^{-{\alpha }_{x}-{\beta }_{x}\mathrm{log}E}$), which leads to ${\beta }_{x}\lt 0.09$ with 90% confidence.

Figure 4 shows the joint fit to the Swift-XRT/NuSTAR data sets for the simultaneous observation performed on April 29. It is apparent that the two observations are in agreement with each other and that, over the entire 1–70 keV energy range, the spectrum of the source can be described (see Table 1) as a simple (very hard) power law with a photon index of 1.06 ± 0.03 absorbed by Galactic gas and dust along the line of sight (Kalberla et al. 2005).

Zoom In Zoom Out Reset image size

2.4. GROND Observations

On 2014 April 26 01:01 UTC PMN J0641−0320 was observed simultaneously in four optical (${g}^{\prime }$, ${r}^{\prime }$, ${i}^{\prime }$, ${z}^{\prime }$) and three NIR (J, H, K) bands with the GROND (Greiner et al. 2008) instrument at the 2.2 m MPG telescope at La Silla Observatory (Chile). Single exposures were obtained with 142 s integrations in the optical bands and 240 s integrations in the NIR bands. Observing conditions were moderate with a seeing of ${1.8}^{\prime\prime }$ and an average airmass of 2.0.

Data reduction and photometry were performed using standard IRAF tasks (Tody 1993), similar to the procedure described in Krühler et al. (2008). The ${g}^{\prime },{r}^{\prime },{i}^{\prime },{z}^{\prime }$ photometry was obtained using PSF fitting while due to the under-sampled PSF in the NIR, the $J,H,{K}_{s}$ photometry was measured from apertures with sizes corresponding to the FWHM of field stars.

The optical photometry was calibrated against an SDSS-field calibrated observation of the same field taken on a different night under photometric conditions. Photometric calibration of the NIR bands was achieved against selected 2MASS stars (Skrutskie et al. 2006) in the field of the blazar.

The resulting AB magnitudes, not corrected for the predicted Galactic foreground reddening of ${E}_{{\rm{B}}-{\rm{V}}}=0.98$ mag (Schlafly & Finkbeiner 2011), are presented in Table 2.

Table 2.  GROND AB Observed Magnitudes of PMN J0641–0320, Taken on UT 2014 April 25 (Magnitudes Not Corrected for Galactic Foreground Extinction)

	${g}^{\prime }$	${r}^{\prime }$	${i}^{\prime }$	${z}^{\prime }$	J	H	Ks
${\lambda }_{{\rm{eff}}}$ (Å)	4587	6220	7641	8999	12399	16468	21706
mag${}_{{\rm{AB}}}$	22.26 ± 0.25	20.76 ± 0.08	20.01 ± 0.08	19.32 ± 0.05	18.40 ± 0.11	18.83 ± 0.12	17.09 ± 0.20

Note. The first row gives the effective wavelength of the filter (in angstroms).

Download table as:  ASCIITypeset image

2.5. Keck Spectrum

We obtained an optical spectrum of PMN J0641–0320 on UT 2014 October 20 using the Low Resolution Imaging Spectrometer (LRIS; Oke et al. 1995), a dual-beam spectrograph on the Keck I telescope atop Mauna Kea. The conditions were poor due to Hurricane Ana, with significant clouds. We observed the target through a 10 slit for two 600 s exposures using the 600 ${\ell }\,{{\rm{mm}}}^{-1}$ grism on the blue arm of the spectrograph (${\lambda }_{{\rm{blaze}}}=4000\,\mathring{\rm A}$, resolving power $R\equiv \lambda /{\rm{\Delta }}\lambda \sim 1000$), the 400 ${\ell }\,{{\rm{mm}}}^{-1}$ grating on the red arm of the spectrograph (${\lambda }_{{\rm{blaze}}}=8500\,\mathring{\rm A}$, $R\sim 1200$), and the 5600 Å dichroic. The data were processed using standard techniques within IRAF, and because no standard stars were taken on that cloudy night, we flux calibrated the spectrum using an archival sensitivity function with the same instrument configuration.

The optical spectrum (displayed in Figure 5) shows strong, red continuum with two emission lines that we identify as broad Mg ii $\lambda 2800$ and narrow [O ii] $\lambda 3727$. The broad line has an observed equivalent width of ∼15 Å and an FWHM$\,\sim \,2000\,{\rm{km}}\,{{\rm{s}}}^{-1}$, clearly indicating a quasar.

Zoom In Zoom Out Reset image size

The Mg ii $\lambda 2800$ line was confirmed a few nights later using Magellan. Our spectroscopic observations thus place the object at a redshift of z = 1.196. Because of its optical and radio properties, PMN J0641–0320 is a new FSRQ.

Figure 6 shows the overall SED of PMN J0641–0320, together with a fitted model. The Swift/XRT and NuSTAR data are strictly simultaneous, while GROND and radio data (provided by the RATAN-600, Trushkin et al. 2014) are quasi-simultaneous. Fermi-LAT data corresponds to a week integration time centered on the NuSTAR pointing (i.e., 3.5 days before and 3.5 days after, see Table 1). The other data are archival (green symbols).

Zoom In Zoom Out Reset image size

The adopted model is described in Ghisellini & Tavecchio (2009). It is a one-zone, homogeneous leptonic model, where the emitting particle distribution is derived through a continuity equation, accounting for continuous injection, radiative cooling, and electron–positron pair production. The resulting energy distribution of the emitting particles $N(\gamma )$ [cm⁻³] is calculated after one light crossing time R/c, where R is the size of the emitting region, assumed to be spherical. As discussed in Ghisellini & Tavecchio (2009), this assumption, suggested by the fast variability of blazars, allows us to neglect adiabatic losses, particle escape, and the changing conditions in the emitting region: since the source is traveling and expanding, the magnetic field and the particle density do not dramatically change in a time R/c.

The injected distribution, of total power ${P}_{{\rm{i}}}^{\prime }$ (primed quantities are calculated in the comoving frame of the source), is assumed to extend between ${\gamma }_{{\rm{\min }}}=1$ and ${\gamma }_{{\rm{\max }}}$ and to be a broken power law smoothly joining at ${\gamma }_{{\rm{b}}}$:

$$\begin{eqnarray}&&Q(\gamma )={Q}_{0}\,\displaystyle \frac{{(\gamma /{\gamma }_{{\rm{b}}})}^{-{s}_{1}}}{1+{(\gamma /{\gamma }_{{\rm{b}}})}^{-{s}_{1}+{s}_{2}}}\,\quad [{\mathrm{cm}}^{-3}\,{{\rm{s}}}^{-1}].\end{eqnarray} \tag{ 1 }$$

The normalization Q₀ is set through ${P}_{{\rm{i}}}^{\prime }=(4\pi /3){R}^{3}\int Q(\gamma )\gamma {m}_{{\rm{e}}}{c}^{2}d\gamma$. The emitting region is assumed to be located at a distance ${R}_{{\rm{diss}}}$ from the black hole. Its size is $R=\psi {R}_{{\rm{diss}}}$, where ψ is the semi-aperture angle of the jet, assumed conical. We assume $\psi =0.1\,{\rm{rad}}$. The model accounts for the accretion disk component, as well as for the IR emission reprocessed by a dusty torus and the X-ray emission produced by a hot thermal corona placed above and below the accretion disk. We have assumed that the accretion disk contributes significantly to the bluest fluxes observed by GROND, and this fixes both the disk luminosity ${L}_{{\rm{d}}}$ and the black hole mass M. We find a black hole mass $M=1.1\times {10}^{9}{M}_{\odot }$ and ${L}_{{\rm{d}}}=6.5\times {10}^{45}$ erg s⁻¹. This model under-reproduces the red part of the GROND SED, which by itself may be fit with a simple power law. This apparent excess may be caused by the oversimplified torus structure assumed by the model, or by some synchrotron emission produced by another component. The ratio of the inverse Compton to synchrotron luminosity (the so-called Compton dominance) is rather large (factor ∼100), in agreement with other powerful blazars. This suggests that the inverse Compton flux benefits from the presence of seed photons produced not only by the synchrotron process (internal to the jet), but also by photons produced externally to the jet, such as the broad line photons and the IR emission produced by the torus. As NuSTAR demonstrates, the X-ray spectrum is intrinsically very hard, and not because of absorption. This indicates that the seed photons coming from the broad line region and the torus are important as seeds for the formation of the high-energy bump, since the synchrotron self-Compton (SSC; Maraschi et al. 1992) process would produce a softer and less powerful luminosity (see the blue dotted line in Figure 6). The large Compton dominance favors two specific locations (see Ghisellini & Tavecchio 2009; Sikora et al. 2009): (i) within the broad line region ("BLR" case), or (ii) outside it, but within the torus ("torus" case). These are the locations where the ratio between the radiation and magnetic energy densities are as large as needed to explain the Compton dominance of the source. However, the size of the emitting zone would be quite different in the two cases, and this corresponds to two different minimum variability timescales, which for our models are about one day for the "BLR" case and five times longer in the "torus" case. The two models produce very similar SEDs, with similar total jet power, even if the bulk Lorentz factors, the injected power, and the magnetic fields are different. Therefore the most promising way to distinguish these models is through variability of the X-ray and γ-ray fluxes, since they are not contaminated by the much steadier contributions of the disk and torus radiation.

If the radiation produced externally to the jet is important, as here, the beaming pattern of the synchrotron radiation is different from the beaming pattern of the inverse Compton process, with the latter more enhanced in the forward direction (Dermer 1995). We take this effect into account. Furthermore, we do not assume ${\rm{\Gamma }}\sim \delta$, but treat both Γ and the viewing angle ${\theta }_{{\rm{v}}}$ as parameters of the model. All velocity vectors of the emitting plasma are assumed to be aligned along the jet axis, in agreement with what is usually assumed for blazars, but contrary to what is usually assumed for the jets of gamma-ray bursts, where the distribution of velocities is assumed to be conical.

The obtained parameters, listed in Table 3, are well within the range of parameters found for other blazars of similar shape and Compton dominance studied and interpreted with the same model (Ghisellini et al. 2010; Ghisellini & Tavecchio 2010, 2015). Since the emitting region is rather compact ($R=2.4\times {10}^{16}$ cm in the "BLR" case and five times that for the "torus" case), its radio emission is self-absorbed (up to ∼400 GHz) and cannot account for the observed radio flux, which must necessarily come from much larger zones.

Table 3.  Parameters of the Model Shown in Figure 6

Model	M	Γ	${R}_{{\rm{diss}}}$	${L}_{{\rm{d}}}$	${P}_{{\rm{i}}}^{\prime }$	B	${\gamma }_{{\rm{b}}}$	${\gamma }_{{\rm{\max }}}$	s1	s2	$\mathrm{log}{P}_{{\rm{r}}}$	$\mathrm{log}{P}_{{\rm{B}}}$	$\mathrm{log}{P}_{{\rm{e}}}$	$\mathrm{log}{P}_{{\rm{p}}}$
[1]	[2]	[3]	[4]	[5]	[6]	[7]	[8]	[9]	[10]	[11]	[12]	[13]	[14]	[15]
BLR	1.1e9	14	240	6.5	0.07	1.25	170	4e3	0.5	3.3	46.6	44.8	45.2	47.6
Torus	1.1e9	17	1.2e3	6.5	0.12	0.07	1e3	2e4	1	3.1	46.9	43.9	46.0	47.6

Note. The two rows correspond to two locations of the dissipation region: the first is within the BLR, the second is outside it, but within the torus. For Figure 7 we use, an an illustration, the parameters of the first row. The spectral shape of the corona is assumed to be $\propto {\nu }^{-1}\exp (-h\nu /150\,{\rm{keV}})$. The X-ray corona emits 20% of the disk luminosity. We have assumed a viewing angle ${\theta }_{{\rm{v}}}=3^\circ$. For ${\rm{\Gamma }}=14$ (17), this implies $\delta =18.2$ (19). Since we assume a conical jet of semi-aperture angle $\psi =0.1\,{\rm{rad}}$, the size of the (assumed spherical) region is $R=\psi {R}_{{\rm{diss}}}$. Thus $R=2.4\times {10}^{16}$ cm for the "BLR" Case, corresponding to a minimum observed variability timescale ${t}_{{\rm{var}}}^{{\rm{obs}}}=R(1+z)/(\delta c)\sim 27\,{\rm{hr}}$. For the "torus" case, $R=1.2\times {10}^{17}$ cm, corresponding to ${t}_{{\rm{var}}}^{{\rm{obs}}}=128\,{\rm{hr}}=5.4$ days. The columns are as follows: Column [1]: model; Column [2]: black hole mass in solar units; Column [3]: bulk lorentz factor; Column [4]: distance of the blob from the black hole in units of 10¹⁵ cm; Column [5]: disk luminosity in units of 10⁴⁵ erg s⁻¹. The radius of the BLR is assumed to be ${R}_{{\rm{BLR}}}={10}^{17}{L}_{{\rm{d,45}}}^{1/2}=2.6\times {10}^{17}$ cm, while the size of the torus is assumed to be ${R}_{{\rm{Torus}}}=2.5\times {10}^{18}{L}_{{\rm{d,}}\,{\rm{45}}}^{1/2}=6.4\times {10}^{18}$ cm. Column [6]: power injected in the blob calculated in the comoving urame, in units of 10⁴⁵ erg s⁻¹; Column [7]: magnetic field in Gauss; Columns [8], [9]: break and maximum random Lorentz factors of the injected electrons; Columns [10] and [11]: slopes of the injected electron distribution $Q(\gamma )$ below and above ${\gamma }_{{\rm{b}}};$ Column [12] logarithm of the jet power in the form of radiation, [13] Poynting flux, [14] bulk motion of electrons, and [15] protons (assuming one cold proton per emitting electron), in erg s⁻¹.

Download table as:  ASCIITypeset image

The total power ${P}_{{\rm{r}}}$ of the emitted bolometric luminosity is of the order of (see e.g., Ghisellini & Tavecchio 2009; Ghisellini et al. 2014b)

$$\begin{eqnarray}&&{P}_{{\rm{r}}}\,\sim \displaystyle \frac{{L}_{{\rm{jet}}}^{{\rm{bol}}}}{{{\rm{\Gamma }}}^{2}}\,\sim 4\times {10}^{46}\,\mathrm{erg}\,{{\rm{s}}}^{-1}.\end{eqnarray} \tag{ 2 }$$

This can be considered to be a lower limit on the total jet power. This cannot be provided by the bulk motion of the relativistic emitting electrons nor by the Poynting flux (see the corresponding values ${P}_{{\rm{e}}}$ and ${P}_{{\rm{B}}}$ in Table 3) and requires the presence of an important proton component that is dynamically dominant. The value reported in Table 3, assuming one cold proton per emitting electron, is ${P}_{{\rm{p}}}\sim 4\times {10}^{47}$ erg s⁻¹, a value much larger (factor 60) than ${L}_{{\rm{d}}}$. Assuming a 10% accretion efficiency, this would imply that ${P}_{{\rm{jet}}}\sim 6\dot{M}{c}^{2}$, twice as much as the maximum value found by McKinney et al. (2012). One can lower ${P}_{{\rm{p}}}$ by assuming that there are some emitting ${{\rm{e}}}^{\pm }$ pairs, but their number cannot exceed ∼10 per proton. In this case ${P}_{{\rm{jet}}}\sim {P}_{{\rm{r}}}$, the entire kinetic energy would be used to produce the radiation we see, and the jet would stop. This limits the possible number of pairs to a few per proton (see discussion in Sikora & Madejski 2000; Celotti & Ghisellini 2008). Alternatively, the assumed accretion efficiency could be smaller than $\eta =0.1$ used here. Indeed, in jetted AGNs, this could be a likely possibility, since part of the gravitational energy could be used not to heat the disk (and thus produce the disk radiation), but to amplify the magnetic field needed to launch the jet (see e.g., Jolley & Kuncic 2008; Jolley et al. 2009).

As it can be seen in Table 3, the ratio ${P}_{{\rm{B}}}/{P}_{{\rm{p}}}$ is small ($\sim 1.6\times {10}^{-3}$ for the BLR model while $\sim 2\times {10}^{-4}$ for the torus model) due to the very large Compton dominance of the source. Table 3 indicates that even in the case of no protons (i.e., a pure pair plasma, that is excluded from the consideration made above), the source would be weakly magnetized. Such small values of ${P}_{{\rm{B}}}/{P}_{{\rm{p}}}$ (and even of ${P}_{{\rm{B}}}/{P}_{{\rm{e}}}$) are a problem for magnetic reconnection as the main particle acceleration mechanism (Sironi et al. 2015).

3.1. The X-Ray Hardness

As mentioned above, the extremely hard slope of the X-ray spectrum, which cannot be due to absorption, strongly suggests that the inverse Compton process uses external photons as seeds. This is due to two reasons:

(i) In the top panel of Figure 7, we show the SED as seen by an observer comoving with the emitting blob. We use the ${\nu }^{\prime }{{\ell }}^{\prime }({\nu }^{\prime })$ versus ${\nu }^{\prime }$ representation, where ${{\ell }}^{\prime }({\nu }^{\prime })$ is the monochromatic compactness, defined as ${{\ell }}^{\prime }({\nu }^{\prime })\equiv {\sigma }_{{\rm{T}}}{L}^{\prime }({\nu }^{\prime })/[{{Rm}}_{{\rm{e}}}{c}^{3}]$ (Cavaliere & Morrison 1980). Since ${\nu }^{\prime }{{\ell }}^{\prime }({\nu }^{\prime })$ is a measure of the optical depth for the pair-production process (becoming important for ${\nu }^{\prime }{{\ell }}^{\prime }({\nu }^{\prime })\gt 1$), the top panel of Figure 7 shows that pair production is marginal. This is confirmed by the relatively small amount of electron–positron pairs produced by the γ–$\gamma \to {e}^{\pm }$ process, shown in the bottom panel of Figure 7, together with the original primary electrons.

Zoom In Zoom Out Reset image size

In the comoving frame of the emitting blob, the photons produced by the disk, the BLR, and the torus are seen, Doppler shifted and aberrated by different amounts, depending on the angle between the photon direction and the velocity vector. For our values of ${R}_{{\rm{diss}}}$, most of the disk radiation, produced by the inner part of the disk, would be seen redshifted in the comoving frame of the blob, and does not contribute much to the seed photons for the inverse Compton scattering process. Much more important are the seeds produced by the BLR and the torus. As long as the blob is inside the BLR (torus), the emission of the BLR (torus) is seen beamed, with a corresponding energy density enhanced by a factor $f{{\rm{\Gamma }}}^{2}$ with respect to an observer stationary with respect to the black hole. The f parameter is of order unity, as long as ${R}_{{\rm{diss}}}\lt {R}_{{\rm{BLR}}}$ (for the BLR case) or ${R}_{{\rm{diss}}}\lt {R}_{{\rm{torus}}}$ (torus case) and its exact value depends on the geometry of the BLR (spherical or flattened) and the torus.

The top panel of Figure 7 illustrates the "BLR" case as shown in Figure 6, but the plotted SED is as observed in the comoving frame of the blob. Most of the seed photons are provided by the BLR, and especially the hydrogen Lyα. The frequency of these photons is seen (in the frame comoving with the blob) at ${\nu }_{{\rm{seed}}}^{\prime }\sim {\rm{\Gamma }}{\nu }_{\mathrm{Ly}\alpha }\sim 3\times {10}^{16}$ Hz. Below ${\nu }_{{\rm{seed}}}^{\prime }$ the inverse Compton process can scatter seed photons of lower frequencies, that are fewer in number. Scattering with relatively cold electrons of $\gamma \sim 1$, photons at ${\nu }_{{\rm{seed}}}^{\prime }$ will remain at the same frequency in the comoving frame, but will be observed at $\delta {\nu }_{{\rm{seed}}}^{\prime }$, which in our case is of the order of ∼2.5 keV. As a consequence, the resulting inverse Compton spectrum is predicted to be hard below this frequency, because of the relative paucity of seed photons below ${\nu }_{{\rm{seed}}}^{\prime }$.

On the other hand the X-ray spectrum of the source continues to be very hard up to ∼70 keV. Therefore, this explanation is not sufficient to account for the hardness across the entire observed X-ray energy range. We thus suggest an additional reason:

(ii) The inverse Compton process efficiently cools the electrons. Electrons above ${\gamma }_{{\rm{cool}}}\sim 5$ radiatively cool in one light crossing time (i.e., they halve their energy). Electrons below this energy radiatively cool in a longer time, and will be affected by adiabatic cooling (important after a doubling time of the source). Assuming that the injection stops after one light crossing time, and calculating the SED at this time, we find that the particle distribution $N(\gamma )$, below ${\gamma }_{{\rm{cool}}}$, retains the injection slope (which is hard in our case: s₁ = 0.5 (namely $N(\gamma )\propto {\gamma }^{-0.5}$ below ${\gamma }_{{\rm{cool}}}$)). This is illustrated in the bottom panel of Figure 7, showing ${\gamma }^{3}\tau (\gamma )$ as a function of γ (where $\tau (\gamma )\equiv {\sigma }_{{\rm{T}}}{RN}(\gamma )$). The ${\gamma }^{3}$ factor allows us to immediately see what electron energies contribute the most at the two peaks of the SED. The very hard electron distribution in the range $1\lt \gamma \lt {\gamma }_{{\rm{cool}}}\sim 5$ corresponds to a very hard spectrum, up to $\delta {\gamma }_{{\rm{cool}}}^{2}{\nu }_{{\rm{seed}}}^{\prime }\sim 75$ keV.

These two factors act together to harden the slope of the X-ray spectrum, making it harder than $F(\nu )\propto {\nu }^{-0.5}$ (equivalent to ${dN}/{dE}\propto {E}^{-1.5}$), which would be typical for fast cooling electrons below ${\gamma }_{{\rm{b}}}$ scattering a fixed amount of soft seed photons. NuSTAR also fixes the X-ray slope up to ∼70 keV, and the very soft Fermi-LAT spectrum constrains the peak of the Compton component to lie in the MeV band. In turn, this constrains both ${\gamma }_{{\rm{b}}}$ and ${\gamma }_{{\rm{cool}}}$ to be smaller than ∼45. If the emitting region were at much larger distances from the black hole, with no external photons, we would have the problem of explaining the large Compton dominance, and also how electrons with $\gamma \gt 45$ cool efficiently.

Very similar considerations can be done for the torus case. In this case ${\gamma }_{{\rm{cool}}}\sim 109$ is larger, but the seed photon frequency (the peak of the IR torus emission) is smaller (we assume a temperature of 370 K) leading to approximately the same inverse Compton frequency peak (see Figure 6).

"MeV blazars" are the most powerful type of blazars and among the most luminous persistent sources in the universe. Their large jet power, accretion luminosity, and black hole mass set them apart from the rest of the jetted AGNs. Despite their high luminosity, only a handful of bona-fide "MeV blazars" were known until recently (Bloom & Marscher 1996; Collmar 2006; Sambruna et al. 2006; Ajello et al. 2009) because of the lack of an MeV telescope surveying the entire sky. However, MeV blazars are characterized by an extremely hard (power-law index <1.5) X-ray continuum and the launch of NuSTAR has uncovered a few new members of the MeV blazar family (Sbarrato et al. 2013; Tagliaferri et al. 2015).

In this paper we report on ToO observations performed by NuSTAR, Swift, and GROND of a flaring source, Fermi J0641−0317, detected by Fermi-LAT in the direction of the anti-center of our Galaxy. These observations showed that the counterpart of Fermi J0641−0317 is PMN J0641−0320 a very bright (8.6 GHz flux of 0.83 Jy) radio source, which our Keck observation places at a redshift of z = 1.196.

The overall SED of PMN J0641−0320, built with contemporaneous and semi-simultaneous observations, unveils several important characteristics. First, PMN J0641−0320 displays, while flaring, the SED of a powerful blazar with a peak luminosity of $L\geqslant {10}^{48}$ erg s⁻¹, a high-energy peak located in the MeV band and a Compton dominance of a factor ∼100. Second, the large Compton dominance suggests that most of the high-energy emission is produced via inverse Compton scattering of the accelerated electrons off an external photon field, very likely the BLR and/or the infrared torus. Our SED modeling suggests a black hole mass of ∼10⁹ ${M}_{\odot }$.

The X-ray continuum, which NuSTAR detects and characterizes up to 70 keV (150 keV in the source frame), is extremely hard and can be characterized by a power law with a photon index of ${{\rm{\Gamma }}}_{X}\approx 1$. This makes PMN J0641−0320 one of the hardest X-ray-emitting blazars and one of the hardest NuSTAR sources. The extreme X-ray hardness is interpreted, in the framework of the external inverse Compton scenario, as produced by a hard electron distribution, which below ${\gamma }_{{\rm{cool}}}\approx 5$ is not cooled, and retains the shape of the injected spectrum, $N(\gamma )\propto {\gamma }^{-0.5}$, and thus causes the very hard X-ray spectrum.

The jet radiative power (${P}_{{\rm{r}}}$ in Table 3), which is a lower limit to the true jet power, is larger than the disk luminosity (${L}_{{\rm{d}}}$ in Table 3), which suggests that the jet is not only powered via accretion, but taps into the rotational energy of the spinning black hole as found for other powerful blazars (Ghisellini et al. 2014b; Tagliaferri et al. 2015).

The hard X-ray continuum, the SED peak location, the large Compton dominance and the high luminosity identify PMN J0641−0320 as a new member of the MeV blazar family. MeV blazars may substantially contribute to the MeV background (Ajello et al. 2009) and can be used to constrain the mass density of heavy black holes (Ghisellini et al. 2010; Sbarrato et al. 2014). The analysis of ∼6 yr of Fermi-LAT data shows that PMN J0641−0320 underwent two rather long flaring episodes. Indeed, it is not unusual for MeV blazars to flare for weeks at a time in γ-rays. This together with the increased sensitivity, due to Pass 8, of Fermi-LAT at <100 MeV might allow us to uncover, in combination with NuSTAR observations, new powerful blazars.

We thank the anonymous referee for useful comments. M.A. acknowledges generous support from NASA grant NNH09ZDA001N. M.B. acknowledges support from the International Fulbright Science and Technology Award and from NASA Headquarters under the NASA Earth and Space Science Fellowship Program, grant NNX14AQ07H.

The Fermi-LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l'Energie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science, and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d'Études Spatiales in France.

This NuSTAR work was supported under NASA Contract No. NNG08FD60C, and made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by the National Aeronautics and Space Administration. We thank the NuSTAR Operations, Software, and Calibration teams for support with the execution and analysis of these observations. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC, Italy) and the California Institute of Technology (USA).

Part of this work is based on archival data, software, or on-line services provided by the ASI Data Center (ASDC). This research has made use of the XRT Data Analysis Software (XRTDAS). Part of the funding for GROND (both hardware and personnel) was generously granted by the Leibniz-Prize to G. Hasinger (DFG grant HA 1850/28-1).

Facilities: Fermi/LAT, NuSTAR, Swift, GROND, Keck.