ABSTRACT
We compare the diversity of spectral line velocities in a large sample of type IIb supernovae (SNe IIb) with the expected asphericity in the explosion, as measured from the light echoes (LEs) of Cassiopeia A (Cas A), which was a historical galactic SN IIb. We revisit the results of Rest et al., who used LEs to observe Cas A from multiple lines of sight and hence determine its asphericity, as seen in the velocity of three spectral lines (He i λ5876, Hα, and the Ca ii near-infrared (NIR) triplet). We confirm and improve on this measurement by reproducing the effect of the LEs in the spectra of several extragalactic SNe IIb found in the literature as well as mean SN IIb spectra recently created by Liu et al. and comparing these to the observed light echo spectra of Cas A, including their associated uncertainties. In order to quantify the accuracy of this comparison, we smooth the light echo spectra of Cas A using Gaussian processes and use a Monte Carlo method to measure the absorption velocities of these three features in the spectra. We then test the hypothesis that the diversity of ejecta velocities seen in SNe IIb can be explained by asphericity. We do this by comparing the range of velocities seen in the different LEs, and hence different lines of sight, of Cas A to that seen in the population of SNe IIb. We conclude that these two ranges are of the same order and thus asphericity could be enough to explain the diversity in the expansion velocity alone.
1. INTRODUCTION
A large number of supernovae (SNe) have been detected and analyzed, leading to a sophisticated classification scheme (Filippenko 1997), which is believed to describe the diversity of the progenitors and explosion conditions. Within this scheme, stripped-envelope SNe (Clocchiatti et al. 1997; Filippenko 1997; Matheson et al. 2001a; Modjaz et al. 2014) constitute a subclass containing about 25% (Li et al. 2011) of all SNe. They occur when a massive star loses some or all of its hydrogen and helium layers before suffering a core-collapse. There are several mechanisms by which the hydrogen and helium layers can be removed, for example, they can be ejected by eruptions, gradually stripped by strong winds (e.g., Woosley et al. 1993) or binary interactions (Nomoto et al. 1995; Podsiadlowski et al. 2004), or burned in the presence of enhanced mixing (Yoon & Langer 2006; Frey et al. 2013). Stripped-envelope SNe are identified observationally by the weakness or absence of hydrogen spectral features (SN IIb and SN Ib respectively), especially at late phases, and by the absence of hydrogen and helium features (SN Ic and SN Ic-bl). The progressive lack of hydrogen and helium in the spectra is the signature of the stripping.
The most extensive spectral data set of stripped-envelope SNe was recently published by Modjaz et al. (2014). Modjaz et al. (2015) and Liu et al. (2016, henceforward L16) showed that there is a great deal of diversity, even within a specific subtype, including within type IIb Supernovae (SNe IIb), which are the focus of our study. SNe IIb have helium and a small amount of hydrogen in their pre-explosion progenitors. In particular, there is a large range of absorption velocities measured for several spectral features. L16 quantified this diversity by constructing mean SN IIb spectra and analyzing the relative standard deviation from these data. This is the first instance of stripped-envelope SN templates in the literature, where the spectral mean behavior and diversity of SNe IIb are systematically quantified.
The question as to the cause of this diversity still remains, but one possibility is that the phenomena from which SNe IIb arise are intrinsically identical but asymmetric and thus the diversity comes from observing along different lines of sight. Asphericity has been observed in many SNe using e.g., polarization (Maund et al. 2007) and double-peaked emission lines (e.g., Maeda et al. 2008; Modjaz et al. 2008), which makes this a plausible scenario. Another technique for determining asphericity uses light echoes (LEs, Couderc 1939; Crotts 1988) to obtain "3D spectroscopy"; this is particularly useful for our purpose since it allows us to observe the spectrum of a source from multiple lines of sight (Boumis et al. 1998; Rest et al. 2011a, 2011b; Sinnott et al. 2013). For long duration transients (such as the great eruption of η-Carine, but also possibly tidal disruption events, super luminous SN, and even for regular SNe in the presence of extremely thin reflecting dust filaments, see Section 3.1), spectroscopic time series can be studied through LEs, assessing the spectroscopic evolution from different lines of sight (Prieto et al. 2014; Rest et al. 2014).
A LE occurs when dust clouds in the vicinity of an object reflect some of the light toward Earth, acting like a mirror. LEs are useful events for many reasons. Because the light must travel a greater distance to Earth than the direct path, the time-of-flight delay allows us to observe historical SNe with modern equipment (Rest et al. 2005, 2008b) and thus classify supernova remnants by their historical SN spectra. Furthermore, if there are multiple LEs, we can observe the same object from multiple lines of sight and hence establish the degree of asymmetry within it (Rest et al. 2011a, henceforward R11). We can then compare this asymmetry to the supernova remnant and to directly observed explosion properties.
To date, there is only one stripped-envelope SN for which spectra from multiple LEs have been obtained.4 Cassiopeia A (Cas A) is a Galactic SN whose light reached Earth in 1681 ± 19 years (Fesen et al. 2006). LEs of the explosions were discovered and studied (Rest et al. 2007, 2008b; Krause et al. 2008a) leading to its spectroscopic classification as a type IIb SN. R11 presented and analyzed spectra of three Cas A LEs. By comparing the absorption velocity of three atomic transition lines in the Cas A spectra with those in the spectra of SN 1993J and SN 2003bg, two well observed SNe IIb, they found that the lines in the Cas A spectra exhibit different absorption velocities when observed from different lines of sight, which is a signature of asymmetry in the explosion. R11 noticed but did not quantify the velocity differences in the LEs. In this work, we wish to quantify this observation of diversity and its statistical significance. Cas A provides a unique opportunity to compare the explosion asymmetry of a single object seen from multiple lines of sight to the diversity of many objects, each seen from a single line of sight, and hence determine if the former could be the cause of the latter.
R11's study of LEs provides the first and, to date, only direct evidence for asymmetry in Cas A; however, asymmetry in the Cas A remnant has been detected in several other studies using a variety of methods. The direct detection of asymmetry in the explosion of Cas A through its LEs, whose statistical significance we determine in the pages that follow, fits a convincing scenario of the asymmetry of the remnant, which strengthens and supports the result. DeLaney et al. (2010) and Milisavljevic et al. (2013) created a 3D picture of the remnant of Cas A (in the IR and X-ray, and optical respectively), using Doppler tomography and proper motion to track the velocities in various parts of the ejecta. By making the assumption that all objects were moving away freely from a single point they were then able to reconstruct a 3D map of the remnant.5 The 3D structure shows that this remnant is far from spherically symmetric. Compact ejecta features, dubbed "knots," discovered by Fesen (2001) and confirmed by Hwang et al. (2004) also reveal asymmetry. Although these knots are mostly isotropic, there is a small group along the southwestern limb moving significantly quicker than the rest. Furthermore, by studying the ratio of 44Ti/56Ni, Nagataki et al. (1998) showed that it was higher than theoretically allowed for a symmetric explosion, and Grefenstette et al. (2014) showed that the distribution of 44Ti as mapped by NUSTAR (Harrison et al. 2013) is not uniform.
In this paper, we provide a statistical assessment of the direct asymmetry of Cas A by comparing the LE spectra with recent spectral templates, and a comparison of the asymmetry of Cas A to the spectral line velocity diversity in the population of SNe IIb.
2. DATA
For our analysis, we used the Cas A light echo data collected and processed by R11, spectra and light curves of individual SNe IIb from the literature, mean SN IIb spectra from L16 and SN IIb template light curves obtained from the data in Bianco et al. (2014). In the following subsections, we describe these data sets.
2.1. Light Echo Data
Three LEs of Cas A were discovered, and their spectra were collected and processed by Rest et al. (2008b) and R11. While we refer to those publications for a detailed description of the data, here we discuss relevant characteristics of the LE spectra.
The data were taken with the Low Resolution Imaging Spectrometer (Oke et al. 1995) on the 10 m Keck I telescope and with the Blue Channel spectrograph (Schmidt et al. 1989) on the 6.5 m MMT. The LEs were originally labeled LE2116, LE2521, and LE3923 by R11; however, hereafter we refer to them by the direction of the line of sight of Cas A that each one probes: SW, NW, and NE, respectively. The LEs are separated by: SW-NW ∼ 70°, SW-NE ∼ 85 5, and NE-NW ∼ 109°, thus truly probing different directions of the explosion. The native resolution of these spectra is around 7 Å and the dispersion is 1 Å for the NE and SW LEs and 2 Å for the NW LE.
5, and NE-NW ∼ 109°, thus truly probing different directions of the explosion. The native resolution of these spectra is around 7 Å and the dispersion is 1 Å for the NE and SW LEs and 2 Å for the NW LE.
For the NW LE, two spectra were taken by R11 at epochs separated by one day, and are analyzed separately in their work. In order to improve the signal-to-noise ratio (S/N) of our measurements, we combine these two spectra into a single spectrum in the wavelength range covered by both, namely  . We smooth (Section 3.2) and renormalize the spectra and use their average, and combine the errors in quadrature.
. We smooth (Section 3.2) and renormalize the spectra and use their average, and combine the errors in quadrature.
2.2. Mean SN IIb Spectra and Light Curves
R11 measured and compared the velocity of the He i λ5876, Hα, and Ca ii near-infrared (NIR) triplet absorption features in the three LE spectra and in the spectra of SN 1993J and SN 2003bg. R11 chose these lines as a metric to measure asymmetry because they are strong, isolated lines in the spectra of SNe IIb, and we expect their absorption velocity (measured as the location of the feature minimum) to approximately track the velocity of the outer envelopes of the star. By looking at this velocity in different directions, we can build a picture of the asymmetry of the SN.
However, since the dust sheets are not perfect reflectors, one cannot compare the light echo spectra directly to each other or to spectra from SNe in the literature, nor can one invert the effect of the dust to recover the emitted spectra. Instead, one must first consider what effects the dust had on the Cas A spectrum and then reproduce those effects in a chosen reference spectrum so that they are comparable. These modeling techniques are described in R11 and by several earlier works (Couderc 1939; Chevalier 1986; Emmering & Chevalier 1989; Sugerman 2003; Patat 2005). The modeling of the effect of reflection on spectra is described in Rest et al. (2011b) and we will use the same LE models, which are also used in Rest et al. (2011a). An in-depth description of the method can be found in these works to which we refer the reader for details, but provide a brief summary in Section 3.1.
In order to simulate the effect of dust scattering, one must take both the spectral and photometric time evolutions into account (Section 3.1). Therefore, R11 chose the spectra of SN 1993J and SN 2003bg as the reference spectra since these SNe IIb are both exceptionally well observed. However, an analysis by L16 revealed that when it comes to our chosen metric, the absorption velocities of the three lines we are focusing on, these SNe are actually some of the most extreme, and have atypical evolutions (e.g., Hα for SN 1993J, see Figure 1). We instead use an SN IIb template that describes the average behavior of SNe IIb as our reference spectra when evaluating the asymmetry of Cas A (Figure 2). The SN IIb spectral template was produced by L16 using 227 spectra of 14 SNe IIb taken from the SuperNova IDentification code spectra library (Blondin & Tonry 2007), the sample presented in Modjaz et al. (2014), and relevant spectra from the literature available before September 2014. Template spectra, i.e., mean spectra, were created at phases ranging from  to +45 in five-day intervals and also at phases 55, 65, 70, 90, 95, and 105 by taking one spectrum from all SNe IIb that had been observed within ±2 days of the target phase and averaging. In addition, in order to retain a measure of the diversity of the SNe spectra that were used for constructing the mean spectra, we adopt the standard deviation spectral arrays provided by L16 and plot them as contours in our plots of the template spectra (Figure 2). Full details of how the template was generated can be found in L16.
to +45 in five-day intervals and also at phases 55, 65, 70, 90, 95, and 105 by taking one spectrum from all SNe IIb that had been observed within ±2 days of the target phase and averaging. In addition, in order to retain a measure of the diversity of the SNe spectra that were used for constructing the mean spectra, we adopt the standard deviation spectral arrays provided by L16 and plot them as contours in our plots of the template spectra (Figure 2). Full details of how the template was generated can be found in L16.
Figure 1. Evolution of velocities of He i λ5876 (upper panel) and Hα (lower panel) for all SNe IIb studied by L16 and from which the SN IIb spectral template was generated. SN 1993J and SN 2003bg (solid symbols) were used in R11 as reference to investigate Cas A's asymmetry. The SNe we use individually in our sample are SN 1993J, SN 1996cb, SN 2003bg, SN 2008ax, SN 2011dh, and SN 2011ei and are plotted in colors here. These SNe are representative of the range of velocities and velocity evolutions observed in the SNe IIb population. Our sample is limited by the need for spectra at a range of phases with high S/N and the need for complete light curves. This is why, e.g., SN 2000H and SN 1998fa are not included.
Download figure:
Standard image High-resolution imageFigure 2. SN IIb mean spectra from L16, and standard deviation in the sample (gray contours), in the wavelength region relevant for the Ca ii NIR triplet (top left), Hα (top right), and He i λ5876 spectral features (bottom left and right). The mean spectra are convolved with the window functions of the three Cas A LEs, which includes the effects of dust, and integration over the photometric evolution. The  window function is simply the integration of the spectra at all epochs weighted by the photometry. The photometric band used for each feature is the band that best covers the wavelength range, and it is noted on the bottom of each plot. For the case of the He i λ5876 line, both V-band and r-band spectra were produced since this feature lies on the overlap of these two bands. The negligible difference between these two spectra justifies our use of a single band for each line and we use V-band normalization for the rest of the paper. For clarity, the standard deviation is shown only for the window function
window function is simply the integration of the spectra at all epochs weighted by the photometry. The photometric band used for each feature is the band that best covers the wavelength range, and it is noted on the bottom of each plot. For the case of the He i λ5876 line, both V-band and r-band spectra were produced since this feature lies on the overlap of these two bands. The negligible difference between these two spectra justifies our use of a single band for each line and we use V-band normalization for the rest of the paper. For clarity, the standard deviation is shown only for the window function  ; however, it is similar when processed through the LEs.
; however, it is similar when processed through the LEs.
Download figure:
Standard image High-resolution imageWe can use these template spectra to confirm the asymmetry of Cas A; however, we cannot use them to determine whether the asymmetry can explain the diversity of absorption velocities seen in SNe IIb. To do this, we look at a selection of the individual SNe that make up the template. Our selection is chosen such that the complete range of absorption velocities is represented, as identified in L16, and in particular, those SNe that have the most extreme velocities are included in our sample. Figure 1 shows the velocity evolution of all SNe studied by L16 and was used to inform our choice. The SNe used, along with the references for their spectra and photometry are: SN 1993J (Jeffery et al. 1994; Barbon et al. 1995; Richmond et al. 1996; Matheson et al. 2000; Fransson et al. 2005; Modjaz et al. 2014), SN 1996cb (Qiu et al. 1999; Matheson et al. 2001a; Modjaz et al. 2014), SN 2011dh (Marion et al. 2014), SN 2003bg (Hamuy et al. 2009), SN 2008ax (Pastorello et al. 2008; Milisavljevic et al. 2010; Bianco et al. 2014; Modjaz et al. 2014), SN 2011dh (Marion et al. 2014), and SN 2011ei (Milisavljevic et al. 2013). Since the Ca triplet feature falls in NIR wavelengths, and NIR spectra of stripped SN are rare, the Ca line comparison cannot be conducted for all SNe in our sample, and we restrict ourselves to only the He i λ5876 and Hα lines for this part of the analysis.
3. METHODS
3.1. Effect of the Dust
The dust sheets that cause the LEs do not act as perfect mirrors, and thus the spectra we observe will not be the same as those emitted by the SN. One reason for this is that the dust sheets have a finite size and thickness, which means that light from multiple epochs in the event timeline will reach the observer at the same time by scattering off different parts of the dust. Therefore, the spectrum we observe in an LE is really the sum of spectra from all epochs weighted appropriately with weights that depend on properties of the dust, of the observation, and on the photometric evolution of the transient, as opposed to that of a single epoch, which would be observed if viewing the SN directly.
Since the effect of this integration cannot be removed from the observed Cas A spectra, we shall process a reference object in such a way as to simulate how it would have appeared had it exploded at the same position as Cas A and been observed in the same LEs. It will then be possible to directly compare the spectra of the reference object and the Cas A LE spectra. For this purpose, a window function (Tylenda 2004; Rest et al. 2011b), w(t), is defined for each LE such that the observed spectrum,  , is related to the emitted spectra,
, is related to the emitted spectra,  , by
, by

It should be noted that the relative normalization of the different epochs that contribute to  is important and thus knowledge of the photometry of the reference object is essential.
is important and thus knowledge of the photometry of the reference object is essential.
Rest et al. (2011b) calculated the window functions of the three LEs of Cas A under study using properties of the dust sheet and the observing slit, the distance from the source and the photometric evolution of the transient. The window functions we use in this work are identical in all respects except where photometry is incorporated and are shown in Figure 3. To apply the window functions correctly, we need flux as a function of time and wavelength, and spectra from each epoch must be weighted appropriately so that they have the correct relative normalization. However, since the spectra we use only have good relative calibration, but not absolute calibration, we must use the corresponding light curves to infer the correct normalization of each spectrum. While R11 used light curves of individual SNe (SN 1993J and SN 2003bg) we must use a light curve relevant to the template spectra of L16 that we use. We must therefore use template SNe IIb light curves derived from the photometric observation of a large sample of SNe IIb. Such light curves have been created by F. B. Bianco et al. (2016, in preparation). Later, when we use individual SN for the comparison, the spectra and light curves of the specific SN will be used.
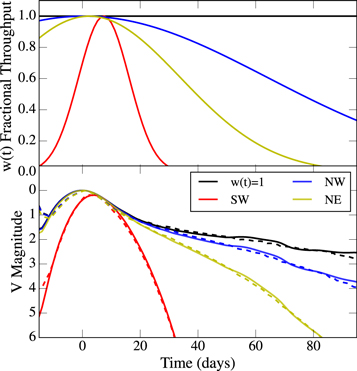
Figure 3. Window functions of the three LEs of Cas A (top panel). Window functions convolved with the SN IIb template V-band light curve (F. B. Bianco et al. 2016, in preparation), showing how much each epoch contributes to the measured spectrum (bottom panel). The black curve is the unmodified template light curve, which corresponds to a window function  . This figure should be compared to Figure 3 in R11 (our lower panel shows their corresponding curves as dashed lines) and differs only in the use of a template light curve as opposed to that of an individual SN (SN 1993J). The differences are small, but noticeable at early times when SN 1993J shows an additional early peak (due to cooling envelope emission), which is not present in our templates after
. This figure should be compared to Figure 3 in R11 (our lower panel shows their corresponding curves as dashed lines) and differs only in the use of a template light curve as opposed to that of an individual SN (SN 1993J). The differences are small, but noticeable at early times when SN 1993J shows an additional early peak (due to cooling envelope emission), which is not present in our templates after  days.
days.
Download figure:
Standard image High-resolution imageSN 1993J, which was used as a reference by R11, has a prominent double peak in its early time photometric data. A double-peaked rise structure is present in several SNe IIb, yet is not universal, and its details are diverse. The double peak is not present in our template for epochs  days. There is therefore a noticeable difference in the window functions shown in Figure 3 and those in R11 (shown as dashed lines), despite the minimal difference in construction.
days. There is therefore a noticeable difference in the window functions shown in Figure 3 and those in R11 (shown as dashed lines), despite the minimal difference in construction.
Furthermore, since it is hard to quantify the effect of reddening due to dust in the SN's host galaxy, we cannot trust the shape of the spectra on large wavelength scales. The templates have therefore been constructed using continuum-subtracted spectra (L16) and assumptions must be made in order to account for the missing continuum. Since we will be focusing only on individual features in the spectra, the assumption that we choose to make is that the continuum varies only on very large wavelength scales and hence is flat throughout the range of wavelengths covered by each feature, which is on the order of 200 Å. With this assumption reinserting the continuum is trivial and each epoch is simply weighted by a single band light curve, observed in the appropriate photometric band for a given feature. Figure 2 shows the template spectra as they would appear in the three LEs of Cas A with each panel focusing on a single feature in the spectrum. For the Ca ii NIR triplet and Hα, the choice of which band to use for normalization is obvious; however, the He i λ5876 line lies directly in between the V and r bands. We therefore use both bands for this line and compare the results. As is evident from this plot, the choice of band is not significant and we therefore use the V band for the remaining analysis.
For some SNe (SN 1993J, SN 2008ax, SN 2011dh, and SN 2011ei) the light curves in the literature do not cover the full range of phases for which spectra have been obtained. For these SNe, we extrapolate the light curve to late phases using a linear extrapolation in log space (magnitudes) by fitting a linear decline to the SN brightness for  , so that we can appropriately normalize all the spectra. A linear extrapolation is consistent with our light-curve templates as well as with the expectation from 56Co decline. We are therefore able to include all observed spectra in our calculations. The window functions only have power for
, so that we can appropriately normalize all the spectra. A linear extrapolation is consistent with our light-curve templates as well as with the expectation from 56Co decline. We are therefore able to include all observed spectra in our calculations. The window functions only have power for  days, as is evident from Figure 3, and therefore spectra taken at later phases than this contribute negligibly to the final spectrum. SN 2011dh and SN 1993J have light curves measured to 80 and 94 days after V-max, respectively, so this extrapolation is of little consequence for these SNe. However, the light curves of SN 2011ei and SN 2008ax are only measured to 33 and 50 days, respectively, and so the extrapolation is more important. For these SNe, we use only the last two points for the extrapolation, since the slope at earlier phases may not be indicative of the SN's decline at late phases. We notice that the last V-band measurement in the light curve of SN 2011ei (Milisavljevic et al. 2013, Figure 3) indicates a very shallow decay rate, much slower than would be extrapolated from the earlier datapoints (the last of which is at
days, as is evident from Figure 3, and therefore spectra taken at later phases than this contribute negligibly to the final spectrum. SN 2011dh and SN 1993J have light curves measured to 80 and 94 days after V-max, respectively, so this extrapolation is of little consequence for these SNe. However, the light curves of SN 2011ei and SN 2008ax are only measured to 33 and 50 days, respectively, and so the extrapolation is more important. For these SNe, we use only the last two points for the extrapolation, since the slope at earlier phases may not be indicative of the SN's decline at late phases. We notice that the last V-band measurement in the light curve of SN 2011ei (Milisavljevic et al. 2013, Figure 3) indicates a very shallow decay rate, much slower than would be extrapolated from the earlier datapoints (the last of which is at  days). While we have no reason to doubt this measurement, and some SN IIb light curves do show flattening after 20 days (Prentice et al. 2016), we felt it was important to test the effect that this datapoint has on our results. We therefore generated two sets of LE spectra for SN 2011ei using two extrapolations of its light curve, one including the measurement at 33 days (a very shallow decline) and one ignoring it (a rather steep decline). The only result affected by this choice is the velocity of the He i λ5876 line seen through the NW LE (whose window function has more power at late times), which changes from −9100 to −9600 km s−1, a small change that leaves the conclusions of this paper intact.
days). While we have no reason to doubt this measurement, and some SN IIb light curves do show flattening after 20 days (Prentice et al. 2016), we felt it was important to test the effect that this datapoint has on our results. We therefore generated two sets of LE spectra for SN 2011ei using two extrapolations of its light curve, one including the measurement at 33 days (a very shallow decline) and one ignoring it (a rather steep decline). The only result affected by this choice is the velocity of the He i λ5876 line seen through the NW LE (whose window function has more power at late times), which changes from −9100 to −9600 km s−1, a small change that leaves the conclusions of this paper intact.
3.2. Calculating the Absorption Velocity
The metric we choose for our comparison is the absorption velocities of three features in the spectrum: He i λ5876, Hα, and the Ca ii NIR triplet, as was done by R11. We employ a Monte Carlo (MC) method, adapted from the one used in L16, to calculate these velocities, the details of which follow. We work separately on each feature by choosing an ∼400 Å region around the expected location of the feature and generate synthetic spectra within that region from the observed flux values and their uncertainties. We then fit a quadratic polynomial to an 80 Å range around the flux minimum for each realization, and take the location of the minimum of the quadratic fit as our velocity measurement, using the relativistic Doppler formula to convert between wavelength and velocity. For the Cas A spectra, we smooth each synthetic spectrum using the Gaussian process described below before fitting the quadratic since the low S/N of these spectra make direct fits unreliable.
The distribution from which our synthetic observations are drawn should be the same as the one our actual observation was drawn from, i.e., the distribution of observations we would expect were we to return to our telescope on several different nights. For the template and the directly observed spectra, it is a good enough approximation to assume that the observed values are close enough to the true spectral flux to draw synthetic observations from a distribution centered on the observed flux. However, due to their low S/N at native spectral resolution, we cannot generally assume that this holds for the LE spectra. Instead of binning the spectra to suppress the noise, we can calculate the correct distribution using Gaussian processes in the following way. We first place a prior on the expected spectrum driven by our expectation that SN spectra vary smoothly. We then condition this prior on the measured spectrum to obtain the final distribution from which our synthetic observations, fi at wavelength  , are drawn. We choose our prior to be an exponential with a mean of zero and a covariance of
, are drawn. We choose our prior to be an exponential with a mean of zero and a covariance of

between any two fluxes measured at wavelengths  and
and  , where
, where  is the velocity of wavelength λ as measured by the relativistic Doppler formula. N and σ are parameters of our model, which represent the S/N and the minimum expected line width respectively. We choose N = 1 and
is the velocity of wavelength λ as measured by the relativistic Doppler formula. N and σ are parameters of our model, which represent the S/N and the minimum expected line width respectively. We choose N = 1 and  km s−1, in order to be consistent with the smoothing algorithm used by R11. The mean vector,
km s−1, in order to be consistent with the smoothing algorithm used by R11. The mean vector,  , and covariance matrix, cov f, of the final distribution from which our synthetic observations are drawn are then
, and covariance matrix, cov f, of the final distribution from which our synthetic observations are drawn are then


where K is the covariance matrix of our prior, with elements 
 , with elements
, with elements  , is a diagonal matrix of the observational errors of our measurements and f* is the observed flux. Full details of this calculation can be found in, e.g., Rasmussen & Williams (2006).
, is a diagonal matrix of the observational errors of our measurements and f* is the observed flux. Full details of this calculation can be found in, e.g., Rasmussen & Williams (2006).
We then generate  simulations where Nλ is the number of wavelength bins within the range of interest (Babu & Singh 1983).6
We smooth each simulated spectrum by the matrix
simulations where Nλ is the number of wavelength bins within the range of interest (Babu & Singh 1983).6
We smooth each simulated spectrum by the matrix  , treat it as an independent observation and process it as we did for the directly observed spectra.
, treat it as an independent observation and process it as we did for the directly observed spectra.
Figure 4 shows the range of velocities found superimposed on the Cas A LE spectra and the template spectra processed through the appropriate window functions.
Figure 4. Comparison of the mean template spectra, processed through the window functions of the three dust sheets (blue solid lines), with the observed spectra of the LEs of Cas A (black solid lines). The shaded light blue bands represent the 1σ variance in the template spectra and the grey bands represent the 1σ observational uncertainty in the Cas A spectra. The observational uncertainty increases dramatically at the location of telluric and night sky lines (for example, the OI night sky line at 5577 Å). Each column displays the same spectral feature: He i λ5876, Hα, and the Ca ii NIR triplet from left to right, and each row displays a light echo: NE, NW, and SW from top to bottom. The positions of the minima of the relevant feature, as calculated using the MC techniques, described in the text are shown as vertical lines for the median values with vertical bands representing the 1σ uncertainty. We see that, for all lines, the velocity in the NW direction is larger than that of the other two directions, confirming R11's result that Cas A is asymmetric.
Download figure:
Standard image High-resolution image4. ANALYSIS OF ASYMMETRY AND DIVERSITY
4.1. Confirming the Asymmetry of Cas A
By comparing the velocity of our three absorption features in the LE spectra of Cas A to those of the template spectra convolved with the relevant window functions of the dust sheets, we can isolate effects due to the asymmetry of Cas A from effects due to differences in the dust sheets. If Cas A were symmetric, we would expect the velocity of Cas A to be the same in all three directions with respect to the template, i.e., we would expect either the line velocities from all three directions to be consistent with the templates or for them all to be faster or all slower by the same amount. Any deviation from this is an indication of asymmetry.
As can be seen in Figure 4 for all three lines the highest velocity, relative to the template velocity, is observed in the NW direction. For the Hα line, we see that Cas A is consistent with the template when seen from the NW direction but has a lower velocity than the templates, with significance  , when seen from the NE direction and
, when seen from the NE direction and  when seen from the SW direction. Similarly, for the Ca ii NIR triplet, Cas A is perfectly consistent with the template when viewed from the NW direction, whereas it is just on the slow end of 1σ consistency in the SW direction and is slower by
when seen from the SW direction. Similarly, for the Ca ii NIR triplet, Cas A is perfectly consistent with the template when viewed from the NW direction, whereas it is just on the slow end of 1σ consistency in the SW direction and is slower by  in the NE. The He i λ5876 line has the largest uncertainty of the three so care must be taken when considering this line. Nevertheless, we see that Cas A has higher velocity than the template, with a significance of
in the NE. The He i λ5876 line has the largest uncertainty of the three so care must be taken when considering this line. Nevertheless, we see that Cas A has higher velocity than the template, with a significance of  when viewed from the NW direction whereas it is consistent at
when viewed from the NW direction whereas it is consistent at  when viewed from the SW and NE directions. The uncertainty in the NE LE in particular is very large for this line, thus, although the velocity is consistent with the templates at
when viewed from the SW and NE directions. The uncertainty in the NE LE in particular is very large for this line, thus, although the velocity is consistent with the templates at  , this has little impact on the significance of our conclusions.
, this has little impact on the significance of our conclusions.
Although we do not find a statistically significant difference in velocity for any individual line by itself, the fact that all three lines show NW as the fastest moving direction, as well as the other evidence for asymmetry of Cas A mentioned in Section 1 leads us to the same conclusion as R11: that Cas A is indeed asymmetric and, in particular, the ejecta is moving more quickly in the NW direction. Furthermore, our calculations strengthen this result since we use mean SN IIb spectra instead of individual SNe and employ MC methods to quantify the differences in velocity more robustly.
4.2. Comparison with the SN IIb Sample
In order to see if this asymmetry, as seen in the Cas A LE spectra, is enough to explain the diversity of absorption velocities seen in our sample of SNe IIb, we repeat the same steps as before, but use the spectra of the individual SNe in our sample as references instead of the template. Figure 5 shows the absorption velocities, as measured by our MC technique, of our selection of SNe IIb processed through the window functions of the three dust sheets, as well as the LEs of Cas A. These measurements are also tabulated in Table 1. The sample of directly observed SNe IIb includes SNe with the most extreme velocities as identified by L16 (see Figure 1), and for the Hα and He i λ5876 lines, measurements of the fastest and slowest well observed SNe in the sample are also plotted separately in Figure 6.
Figure 5. Comparison of the absorption velocity of directly observed SNe IIb, processed through the window functions of the relevant dust sheets, with the measured velocity of Cas A in those LEs. The error bars for the reference SNe are included, but in many cases lie within the markers. In the right panel, the velocity difference between the fastest SN and Cas A, and between the slowest SN and Cas A, are plotted for each light echo for the He i λ5876 (top) and Hα lines (bottom). The box around each set of measurements represents the  confidence region for the velocity difference, including the errors on Cas A and on the SN measurements. The Cas A velocities span the complete range of diversity seen in SNe IIb with some laying at the high end of the distribution (e.g., NW He I λ5876) and others at the low end (e.g., NE Hα) supporting our hypothesis that at this stage the observed diversity can be explained purely through asphericity. Only two of the SNe IIb in our sample had enough NIR spectral data to enable a reliable simulation of the effects of LE reflection. Therefore, the objects shown for this line do not represent the full diversity of SNe IIb, and the line is omitted from the right panel.
confidence region for the velocity difference, including the errors on Cas A and on the SN measurements. The Cas A velocities span the complete range of diversity seen in SNe IIb with some laying at the high end of the distribution (e.g., NW He I λ5876) and others at the low end (e.g., NE Hα) supporting our hypothesis that at this stage the observed diversity can be explained purely through asphericity. Only two of the SNe IIb in our sample had enough NIR spectral data to enable a reliable simulation of the effects of LE reflection. Therefore, the objects shown for this line do not represent the full diversity of SNe IIb, and the line is omitted from the right panel.
Download figure:
Standard image High-resolution imageFigure 6. Comparison of the absorption velocity of the fastest, and slowest SNe from our SNe IIb sample processed through the window functions of the relevant dust sheets with the measured velocity of Cas A in those LEs. These are the same data shown in Figure 5, but grouped by SN and only showing those SNe with the most extreme velocities. The error bars for the reference SNe are included, but in many cases lie within the markers. The effects of the reflection in the dust, simulated through the application of the appropriate window function, determines the difference in the three velocities of each SN. Notice that the effect of dust reflection from the NW light echo decreases the velocity in the directly observed SNe, but for Cas A spectra from this light echo shows the fastest velocity, proving that material is ejected at higher speed in this direction.
Download figure:
Standard image High-resolution imageTable 1.
Line Velocities, in Units of  , as Seen Through the LEs, for Different SNe IIb.
, as Seen Through the LEs, for Different SNe IIb.  Uncertainties are Shown in Parentheses
Uncertainties are Shown in Parentheses
| Cas A | Template | sn2003bg | sn2011ei | sn1993J | sn1996cb | sn2008ax | sn2011dh | ||
|---|---|---|---|---|---|---|---|---|---|
| He i | |||||||||
| NE | −10.58 (−4.37) | −8.06 (−0.84) | −8.11 (−0.03) | −9.53 (−0.08) | −7.58 (−0.06) | −7.58 (−0.06) | −8.56 (−0.02) | −7.52 (−0.03) | |
| NW | −10.88 (−1.68) | −7.71 (−0.79) | −8.09 (−0.03) | −9.14 (−0.09) | −7.36 (−0.05) | −7.37 (−0.06) | −7.99 (−0.03) | −7.53 (−0.03) | |
| SW | −9.25 (−1.60) | −8.48 (−0.82) | −8.11 (−0.03) | −9.74 (−0.08) | −7.72 (−0.05) | −7.85 (−0.08) | −8.84 (−0.02) | −7.51 (−0.03) | |
| Hα | |||||||||
| NE | −9.41 (−0.52) | −11.93 (−1.23) | −13.23 (−0.05) | −13.12 (−0.12) | −10.57 (−0.07) | −11.11 (−0.05) | −14.09 (−0.11) | −12.30 (−0.02) | |
| NW | −12.03 (−0.17) | −11.52 (−1.42) | −13.21 (−0.06) | −13.06 (−0.17) | −10.10 (−0.07) | −10.86 (−0.06) | −13.21 (−0.08) | −12.31 (−0.02) | |
| SW | −11.15 (−1.38) | −12.33 (−1.08) | −13.19 (−0.05) | −13.14 (−0.14) | −10.87 (−0.05) | −11.53 (−0.09) | −14.09 (−0.07) | −12.13 (−0.02) | |
| Ca ii | |||||||||
| NE | −5.98 (−0.47) | −9.37 (−1.58) | −9.74 (−0.17) | −9.96 (−0.84) | ⋯ | ⋯ | ⋯ | ⋯ | |
| NW | −9.09 (−0.12) | −8.97 (−1.58) | −9.74 (−0.17) | −9.89 (−1.30) | ⋯ | ⋯ | ⋯ | ⋯ | |
| SW | −8.12 (−0.44) | −9.14 (−1.49) | −9.77 (−0.16) | −10.01 (−0.45) | ⋯ | ⋯ | ⋯ | ⋯ |
Download table as: ASCIITypeset image
For both the He i λ5876 and Hα lines, the velocity of Cas A is consistent to within  with the velocity of either the fastest, or slowest SNe in our sample in at least one LE. Because of this, we cannot rule out that the diversity observed in SNe IIb, as measured from the blueshift velocity of the lines, is entirely due to asymmetry in the explosion, while the kinetic energy per unit mass could be identical for all objects in the sample. Meanwhile, diversity in the kinetic energy per unit mass may of course manifest itself in other observables, for example, in luminosity, line ratios, or temperatures, which our analysis does not probe.
with the velocity of either the fastest, or slowest SNe in our sample in at least one LE. Because of this, we cannot rule out that the diversity observed in SNe IIb, as measured from the blueshift velocity of the lines, is entirely due to asymmetry in the explosion, while the kinetic energy per unit mass could be identical for all objects in the sample. Meanwhile, diversity in the kinetic energy per unit mass may of course manifest itself in other observables, for example, in luminosity, line ratios, or temperatures, which our analysis does not probe.
Again we notice that the velocity difference between the different LEs of Cas A is greater than that of any other SN in our sample, especially in Hα, again highlighting that the asymmetry of Cas A is real, and not just an artifact of the differences in the dust sheets (while in our sample of SNe IIb each object is, of course, seen only from a single line of sight, and all differences in the different panels arise from the convolution with different LE window functions).
In Figure 6, only the SNe with the most extreme velocities are plotted, and the velocities are grouped by SN. Data points with the same symbol, representing the same LE, should be compared, and we see the following.
- 1.While the velocities of the reference SNe are only slightly affected by the different window functions, a big difference between the LEs of Cas A is seen, which we attribute to a direct detection of asymmetry in Cas A. This effect is even more apparent when one considers that, for most of the reference SNe, the window function of the NW dust sheet causes the feature to appear slower, whereas for Cas A, the velocity in this direction is consistently the highest of the three (Figure 6).
- 2.Some of the velocities of Cas A are consistent with the fastest SNe IIb (e.g., NW He i λ5876), whereas others are consistent with the slowest (e.g., NE Hα). Thus the range of velocities seen in the LEs of Cas A is of the same order as the spread of velocities in our sample of SNe IIb, indicating that the asymmetry of Cas A, if common among SNe IIb, would manifest itself as diversity in a sample of directly observed SNe IIb consistent with that which we observe.
- 3.For all lines and all directions there is at least one SN IIb whose velocity difference from Cas A is consistent with 0 within
 (see the right panel of Figure 5). This shows that Cas A is not an outlier of the distribution of velocities in SNe IIb and hence that treating the asymmetry of Cas A as typical is a justified assumption.
(see the right panel of Figure 5). This shows that Cas A is not an outlier of the distribution of velocities in SNe IIb and hence that treating the asymmetry of Cas A as typical is a justified assumption. - 4.The SNe IIb displaying the most extreme velocities in He i λ5876 are not the same objects that show extreme velocities in Hα. In fact, for all LEs, Cas A has high He i λ5876 velocities, but low Hα compared to our sample and our template.
5. CONCLUSIONS
In this work, we have re-analyzed the light echo spectra of Cas A discovered and studied by R11 in order to quantify its asphericity, as traced by spectral line velocities seen from different directions. We also tested the hypothesis that asphericity, as measured in Cas A, is enough to explain the diversity of spectral line velocities seen in extragalactic SNe IIb (in each case, seen only along one line of sight).
We have confirmed the result of R11 by showing that the velocities of the He i λ5876, Hα, and Ca ii NIR triplet lines in Cas A are all larger when viewed from the NW direction, even after considering the effect of the dust sheets that produce the LEs by reproducing the effects in reference spectra. We have strengthened R11's result by using mean SN IIb spectra as a reference, as well as several individual SNe IIb, thereby showing that this result is not sensitive to the choice of reference. We have determined uncertainties on our velocity measurements of template, individual SNe, and light echo spectra through MC methods so that we can make the comparisons more robustly and can assess the statistical significance of the result we present.
The range of velocities due to the asymmetry of Cas A is of the same order as the range observed in the population of SNe IIb and thus the velocity diversity in the observed sample of SNe IIb is consistent with being induced by asymmetry, even in the presence of explosions with identical kinetic energy per unit mass that are asymmetric to the level of Cas A. We thus cannot rule out the possibility that the velocity diversity seen in SNe IIb is due to their intrinsic asymmetry, especially when we consider the possibility that there is another direction moving even faster than NW, or slower than SW and NE, but which does not have a corresponding observed LE. Our result indicates that asymmetry has a significant contribution in determining the observed diversity of spectral velocities within SNe IIb. Observations of other SNe IIb with multiple LEs would be the best way to strengthen this result, since currently there is no way to exclude the possibility that Cas A is more asymmetric than a typical SN IIb. Additional objects could confirm whether asymmetry in SNe IIb is common, and quantify the contribution of asymmetry to the spread in line velocities seen in the directly observed SNe IIb. The analysis in this paper has been limited to the diversity in line velocities; however, other measurements, such as line flux ratios or temperature, may also indicate additional diversity, which we do not probe here.
Another interesting observation is that the SNe that are most extreme in one spectral feature are not necessarily as extreme in another. In particular, SN 2011dh has one of the slowest He i λ5876 lines in our sample, yet in the Hα, it is average, or even among the faster SNe. This may indicate that different envelopes of the SN move at different velocities. Cas A itself shows high He i λ5876 velocities, but lower  velocities, for all LEs, when compared to the directly observed SNe.
velocities, for all LEs, when compared to the directly observed SNe.
Our result is limited by the small sample size for both LEs and well observed SNe IIb. This of course will change in the near future: modern and future synoptic surveys, starting with PTF (Law et al. 2009; Rau et al. 2009), PanSTARRS (Tonry et al. 2012), DECAM (The Dark Energy Survey Collaboration 2005), ZTF (Smith et al. 2014), and culminating with LSST (LSST Science Collaboration et al. 2009), are discovering SNe at an ever increasing rate. Studies like ours require dense spectroscopic time series, which will be limited to the closest few objects, but it is undoubtable that our understanding of the diversity of SNe IIb and other SN subtypes will dramatically improve in the years to come. LEs as well will be discovered at a much higher rate in the LSST age, with the increased sky coverage at faint magnitude. Here too we will need the largest telescopes to collect spectra of the low surface brightness LEs, but the sample of SNe with direct asymmetry constraints should increase. This will not only allow us to reproduce this study and obtain a more statistically significant result, but also to extend this investigation of how asymmetry contributes to observed diversity, and how intrinsically diverse SNe that are classified within the same subtype are, to other SN classes. For example, while LEs of the S/N Tycho have been observed (Rest et al. 2007), which indicate that it was an SN Ia (e.g., Krause et al. 2008b; Rest et al. 2008a), it would be crucial to obtain spectra of LEs that arose from different viewing angles in order to constrain the degree of asphericity in SNe Ia. This could help constrain their progenitors since, for example, the head-on collision of white dwarfs in a triple system (Kushnir et al. 2013) claims large asphericities (Dong et al. 2015).
We are grateful to Robert Speare, Michael Blanton, Saurabh Jha, and Or Graur for useful discussions and Niloufar Khavari for preliminary work on this project. We thank the referee for helpful suggestions that improved the quality of the paper.
K.F. is supported in part by the US-UK Fulbright Commission All-Disciplines Postgraduate Award. F.B.B. is supported in part by the NYU/CCPP James Arthur Postdoctoral Fellowship. M.M. is supported in part by the NSF CAREER award AST-1352405 and by the NSF award AST-1413260. Y.Q.L. is supported in part by the NSF award AST-1413260 and by a NYU/CCPP James Arthur Graduate Award. A.R. was supported in part by the HST programs GO-12577 and AR-12851.
Footnotes
- 4
- 5
An interactive version of this map, created by Dan Milisavljevic, is available online at https://www.cfa.harvard.edu/~dmilisav/casa-webapp/model.html.
- 6
This is proven to be an appropriate number of draws for bootstrapping. By extension, we assume it is an appropriate number of draws for our MC simulations.