Habitable Moist Atmospheres on Terrestrial Planets near the Inner Edge of the Habitable Zone around M Dwarfs

Here, we use a modified version of the Community Atmosphere Model version 4 (CAM4) from the National Center for Atmospheric Research in Boulder, Colorado (Neale et al. 2010). We use $4^\circ \times 5^\circ$ horizontal resolution, with 40 verticals levels extending to a model top of ∼1 mbar. For all simulations we assume a planet with Earth radius, mass, and gravity. The atmosphere is taken to consist only of ${{\rm{N}}}_{2}$ and ${{\rm{H}}}_{2}{\rm{O}}$. Other species such as O₂, O₃, CO₂, CH₄, and trace gases have been removed for simplicity, and habitable planets with active carbonate-silicate cycles should have low CO₂ levels if their surface temperatures are hot. Thus, here our calculation of the inner edge of the habitable zone represents an innermost boundary. The addition of other greenhouse gas species would serve only to push the inner edge of the HZ farther away from the star. The total pressure of the atmosphere is given as ${P}_{\mathrm{tot}}={P}_{{{\rm{H}}}_{2}{\rm{O}}}+{P}_{{{\rm{N}}}_{2}}$, where P_x is the partial pressure of each gaseous component. ${P}_{{{\rm{N}}}_{2}}$ is set to 1 bar in all simulations, while atmospheric water vapor varies self-consistently depending on the temperature and relative humidity of the atmosphere.

We assume an aquaplanet (i.e., an entirely ocean-covered planet with no land), with a 50 m deep thermodynamic "slab" ocean (Bitz et al. 2012). Ocean heat transport is to set to zero everywhere. While we focus on the inner edge of the HZ, many of our simulations still have ice cover. We include sea ice using the Los Alamos sea-ice model CICE version 4 (Hunke & Lipscomb 2008). We use the default albedo parameterization, which divides ocean, sea ice, and snow albedos into two bands: visible and near-IR divided at 0.7 μm. Following Shields et al. (2013), we set the visible (near-IR) sea-ice albedo to 0.67 (0.3), the snow albedo to 0.8 (0.68), and the ocean albedo to 0.07 (0.06), respectively.

We use the finite-volume (FV) dynamical core (Lin & Rood 1996). The FV dynamical core has been modified to improve numerical stability (courtesy of C. Bardeen). This entails incrementally applying physics tendencies for temperature and wind speed evenly throughout the dynamical substeps. Note that several additional sensitivity tests were conducted using the spectral element dynamical core on a cubed-sphere grid (Lauritzen et al. 2014). We use physics time steps of 30 minutes with 48 dynamical substeps per physics time step. The radiative transfer is calculated once every 90 minutes. All simulations are initiated with surface temperatures matching that of the modern Earth. Simulations are run until they enter a runaway state or reach statistically steady state, which typically takes about 40 Earth years.

Previous calculations of the inner edge of the HZ for tidally locked planets around late K and M dwarf stars were conducted with CAM3 and CAM4 (Yang et al. 2014; Wang et al. 2016; Kopparapu et al. 2016), using the native (i.e., unmodified) radiative transfer code. According to the scientific description of CAM,⁹ the long-wave radiative transfer is based on the broadband model approach described by Kiehl & Briegleb and Kiehl & Ramanathan. The short-wave radiative transfer uses the δ-Eddington approximation described in Briegleb (1992), across a coarse pseudo-spectral grid. Absorption by water vapor is based on the HITRAN2000 line database (Rothman et al. 2003) and incorporates the Clough, Kneizys, and Davies (CKD) 2.4 prescription for the continuum (Clough et al. 1989). Recently it was shown that the native CAM radiative transfer code significantly underestimates absorption by water vapor in both the long wave and the short wave (Yang et al. 2016). This means that the inner edges of the habitable zone defined by Yang et al. (2014) and Kopparapu et al. (2016) are both placed too close to the host star.

Yang et al. (2016) also indicate that the radiative transfer code first described by Wolf & Toon (2013) and later used by Wolf & Toon (2014, 2015) to study moist greenhouse atmospheres for Earth around the Sun does well in the long wave against its reference model (LBLRTM), but absorbs too much solar radiation for warm (${T}_{s}\gt 300\,{\rm{K}}$), saturated atmospheres. Another result to emerge from Yang et al. (2016) is that spectral resolution in the near-IR is critical for accurately calculating short-wave radiative transfer in water-rich atmospheres. Here, we improve on the radiative transfer scheme first described in Wolf & Toon (2013), by implementing a new correlated-k approximation using the latest spectral database, HITRAN 2012, and by increasing the spectral resolution in the near-IR. New k-coefficients were created using HELIOS-K, a new open-source spectral sorting program designed for graphics processing units (Grimm & Heng 2015). The utilization of massively parallel graphics processing units enables a several-order-of-magnitude increase in computational efficiency. This allowed us to test numerous different spectral resolutions and achieve an optimal balance of speed and accuracy for our project. We settled on a 42 spectral interval grid ranging from 10 to 50,000 cm ⁻¹, with 8 Gauss points per interval. The short-wave stream is computed over 35 spectral intervals from 820 to 50,000 cm⁻¹. The long-wave stream is computed over 19 spectral intervals from 10 to 4000 cm⁻¹.

We only consider absorption by ${{\rm{H}}}_{2}{\rm{O}}$, with the correlated k-coefficients calculated for a pressure grid from 10 bar to 0.01 mbar with successive pressure levels following log10(P1/P2) = 0.1, and a temperature grid from 100 to 500 K with ${\rm{\Delta }}T=25$ K. Furthermore, we have implemented a new water-vapor continuum parameterization, following the formalism of Paynter & Ramaswamy (2011). This continuum treatment is derived from laboratory measurements taken at temperatures appropriate for atmospheres expected near the inner edge of the habitable zone and is stronger than the commonly used MT-CKD continuum. Finally, we have implemented direct integration by midlayer Planck functions to correct some unphysical sawtoothing of heating rates found near the model top in previous versions. We use the two-stream radiative transfer solver from Toon et al. (1989).

Cloud overlap is treated using the Monte Carlo Independent Column Approximation (MCICA), assuming maximum-random overlap (Pincus et al. 2003). MCICA uses stochastically generated subcolumns to represent subgrid-scale cloud variability. Subcolumns are then randomly sampled across the spectral integration. MCICA is specifically designed for use in 3D models and is well tested in both GCMs (Barker et al. 2008) and numerical weather prediction models (Hill et al. 2015).

To test our code, we follow the methods of Yang et al. (2016), using clear-sky saturated atmospheric profiles with surface temperatures ranging from 250 to 360 K, and 200 K isothermal stratospheres. For short-wave calculations we assume a 3400 K blackbody stellar spectrum as input. In Figure 1 we compare results from our correlated-k radiative transfer code with that from a line-by-line code, LBLRTM (Clough et al. 2005), for both the long wave and short wave. Calculations of both outgoing long-wave radiation (OLR) and absorbed short-wave radiation (ASR) remain within ∼3 W m⁻² compared with LBLRTM for all atmospheric profiles tested. This is accurate to within about $\sim 1 \%$ with respect to OLR and ASR. Accuracy is substantially improved compared to previous iterations of our correlated-k code and also compared to the native CAM radiative transfer (Yang et al. 2016).

Zoom In Zoom Out Reset image size

Condensation, precipitation, and evaporation use the bulk microphysical parameterizations of Rasch & Kristjánsson (1998). Deep convection is treated using the parameterization of Zhang & McFarlane (1995). This scheme has been improved to include convective momentum transport and dilute entraining plumes (Raymond & Blyth, 1986, 1992). The deep convection scheme uses a plume ensemble approach, where convective updrafts and downdrafts occur wherever the low atmosphere becomes conditionally unstable. The entropy closure calculation within the deep convection scheme has been updated (courtesy of C.A. Shields) to use the more robust numerical approach of Brent (1973). A secondary convective parameterization treats shallow convective overturning at all layers in the atmosphere (Hack 1994). CAM4 self-consistently accounts for changing atmospheric pressures due to changing water-vapor amounts in each grid cell. The total grid cell mass is determined from tendencies imparted by advection, convection, turbulent mixing, and large-scale stable condensation and evaporation. CAM4 uses virtual temperature corrections to account for variations in density, and a similar approach accounts for the variation in specific heat between moist and dry air.

Cloud fractions are determined for three separate types of clouds. Marine stratus cloud fractions depend on the stratification of the atmosphere between the surface and the 700 mbar level. Convective cloud fractions depend on the stability of the atmosphere and the convective mass flux. Layered clouds at all altitudes depend on the relative humidity and the pressure level. Cloud liquid droplet radii are assumed to be $14\,\mu {\rm{m}}$ everywhere in the model. Ice cloud particle effective radii follow a temperature-dependent parameterization and can vary in size from a few tenths to a few hundred microns. A typical ice cloud in the model has an effective radius of ∼50 μm at air temperatures of 240 K and $\sim 20\,\mu {\rm{m}}$ at air temperatures of 200 K.

We conduct simulations for planets around stars with effective stellar temperatures of 2600, 3000, 3300, 3700, 4000, and 4500 K. We assume that all of our planets are in synchronous rotation with their host stars. Leconte et al. (2015) argue that planets are expected to have a nonsynchronous rotation if they are in the habitable zone of stars more massive than ∼0.5 to $0.7\,{M}_{\odot }$ (depending on their location in the habitable zone). Our stellar properties remain below this limit. The orbital period and thus the planetary rotation rate of each case are calculated self-consistently with Kepler's laws, following Equation (3) in Kopparapu et al. (2016). The stellar effective temperature, mass, luminosity, stellar flux at the planet, and planetary rotation rate are strictly intertwined. We repeat the equation from Kopparapu et al. (2016), as this is critical in choosing our rotational periods of planets in our simulations:

$$\begin{eqnarray}&&P(\mathrm{years})=\left[{\left(\displaystyle \frac{{L}_{\star }/{L}_{\odot }}{{F}_{P}/{F}_{\oplus }}\right)}^{3/4}\right]{[{M}_{\star }/{M}_{\odot }]}^{-1/2},\end{eqnarray} \tag{ 1 }$$

where P is the orbital period of the planet (for synchronous rotation, it is also the rotational period), ${L}_{\star }/{L}_{\odot }$ is the luminosity of the star with respect to the bolometric luminosity of the Sun, ${F}_{P}/{F}_{\oplus }$ is the stellar flux incident on a planet (F_P) compared to the flux on Earth (F_⊕), and ${M}_{\star }/{M}_{\odot }$ is the stellar mass in solar mass units. This equation indicates that the orbital period of a planet in synchronous rotation can be calculated from the luminosity, mass, and incident flux, and it cannot be chosen irrespective of the stellar type. We then use a parameterized relationship between T_eff, M_⋆, and L_⋆ (as shown in Table 1 of Kopparapu et al. 2016) to choose a specific stellar temperature. A list of simulations with stellar and planetary characteristics shown in Figures 3–5 is tabulated in Table 1.

Table 1.  Simulation Cases Shown in Figures 3–5

Teff (K)	L/L⊙	M/M⊙	FP/F⊕	P(days)	Model Top ${{\rm{H}}}_{2}{\rm{O}}$ Mixing Ratio (1 mbar)
4500	0.189	0.72	1.323	100.20	2.97 × 10−6
			1.470	92.59	7.04 × 10−5
			1.617	86.20	1.41 × 10−3 (water loss)
			1.654	84.76	7.41 × 10−3
			1.691	83.37	1.79 × 10−2
			1.727	82.04	(runaway)
4000	0.0878	0.628	1.176	65.79	1.76 × 10−5
			1.323	60.23	3.61 × 10−4
			1.397	57.83	1.48 × 10−3
			1.470	55.65	1.64 × 10−2 (water loss)
			1.507	54.63	(runaway)
3700	0.0429	0.520	1.102	44.33	2.19 × 10−5
			1.176	42.24	7.85 × 10−5
			1.323	38.66	2.89 × 10−3 (water loss)
			1.397	37.13	2.82 × 10−2
			1.433	36.41	(runaway)
3300	0.00972	0.249	1.029	22.12	3.41 × 10−5
			1.176	20.02	1.24 × 10−4
			1.213	19.57	5.55 × 10−4
			1.250	19.13	7.60 × 10−3 (water loss)
			1.280	18.72	(runaway)
3000	0.00183	0.143	0.955	8.83	4.14 × 10−5
			1.029	8.35	2.12 × 10−4
			1.103	7.93	2.57 × 10−4
			1.139	7.74	5.14 × 10−4
			1.158	7.65	6.39 × 10−4
			1.176	7.56	(runaway, no water-loss limit)
2600	0.000501	0.0886	0.882	4.51	7.71 × 10−7
			0.919	4.37	3.13 × 10−6
			0.955	4.25	1.18 × 10−5
			0.992	4.13	6.94 × 10−5
			1.011	4.07	(runaway, no water-loss limit)

Note.  For a given stellar effective temperature (T_eff), the stellar luminosity ($L/{L}_{\odot }$), mass ($M/{M}_{\odot }$) and incident stellar flux on the planet (${F}_{P}/{F}_{\oplus }$) are related to the orbital period P through Equation (1). We assume synchronously rotating planets, so the orbital period = rotational period. The last column is the amount of ${{\rm{H}}}_{2}{\rm{O}}$ available at the model top (1 mbar) and also indicates the transition stages to water loss and runaway greenhouse limits.

Download table as:  ASCIITypeset image

For stars with ${T}_{\mathrm{eff}}\gt 3200$ K, we use the empirically derived relationships between the mass, luminosity, and effective temperature of the host stars from Boyajian et al. (2013). These relationships are valid for stellar metallicities ranging from [Fe/H] = −0.5 to +0.1 dex. Note that Boyajian et al. (2013) conclude that metallicity only affects the color index of a star; however, metallicity does not appear to impact the global properties of a star: temperature, radius, and luminosity. Stars with ${T}_{\mathrm{eff}}\lt 3200$ K fall outside the validity range for the fits provided by Boyajian et al. (2013). Thus, in this regime we use the stellar properties from the Baraffe et al. (2002) stellar evolutionary models, assuming an age of ∼3 Gyr (log t(yr) = 9.50). For all cases, we use stellar spectra from the BT-SETTL grid of models (Allard et al. 2003, 2007), assuming a stellar metallicity of [Fe/H] = 0.0. We conduct simulations for planets under increasing stellar fluxes, until a runaway greenhouse is triggered.

The Spectral Mapping Atmospheric Radiative Transfer Model (SMART) is a versatile line-by-line fully multiple scattering 1D radiative transfer model (Meadows & Crisp 1996), capable of simulating a wide variety of planets. It has been validated against solar system objects (Arney et al. 2014; Robinson et al. 2014) and has been used to study a wide variety of types of atmospheres (Robinson et al. 2011; Arney et al. 2016; Schwieterman et al. 2016; Charnay et al. 2015). SMART has been modified to calculate transit spectra, including the effects of refraction (Misra et al. 2014). Transit spectra can be generated from GCM results by using atmospheric columns from the planetary terminator region.

We use PandExo, a publicly available simulator for JWST and HST. PandExo is described extensively in Batalha et al. 2017, but we briefly describe it here. PandExo relies on STScI's exposure time calculator Pandeia (Pontoppidan et al. 2016) to compute pixel-level simulations based on the most up-to-date instrument characterization data. Therefore, it includes simulations of throughputs, background noise, read noise, point-spread functions, optical paths, and saturation levels. However, it does not fully simulate detector systematics, which have been suggested to create a noise floor of 20–30 ppm for the near-IR instruments and 50 ppm for MIRI (Greene et al. 2016). It also does not simulate any time-varying noise sources such as stellar variability or spacecraft jitter and drift, which could add to JWST's systematic noise floor (Barstow et al. 2015).

First, we compare several sets of idealized simulations of synchronously rotating planets in order to determine the effect on climate of our updates to the radiative transfer code. In Figure 2 for all simulations we assume 3400 K blackbody stellar spectra, and we fix the planetary rotation to a 60-day synchronous orbit for all values of the incident stellar flux. The blackbody spectra and fixed 60-day rotation rate were chosen specifically to facilitate comparison with Yang et al. (2013). We also assume a completely ocean-covered world with no ocean heat transport. Here, we compare CAM simulations using our new radiative transfer code, along with several results that use the native CAM radiative transfer scheme found in versions 3 and 4 of the model (Briegleb 1992). Yang et al. (2013) used CAM3 with the spectral Eulerian dynamical core, Kopparapu et al. (2016) used CAM4 with the finite-volume dynamical core, and we additionally test CAM4 with the native radiative transfer scheme and the spectral element dynamical core on a cubed-sphere grid (Lauritzen et al. 2014). Results from these three configurations, all using the native CAM radiative transfer (dashed lines), tend to cluster together irrespective of the choice in dynamical core and also independent of differences in the assumed planetary properties. Note that Yang et al. (2013) simulations assume a planet of radius 2 ${R}_{\oplus }$ and a surface gravity of 1.4 g, while the others assume 1 Earth mass and Earth-like gravity.

Zoom In Zoom Out Reset image size

Note that some past studies have found that the CAM finite-volume dynamical core failed to capture the upper atmosphere superrotating winds of Titan and Venus (Parish et al. 2011; Lebonnois et al. 2012; Larson et al. 2014). However, here we find no resultant differences in surface climate for slow-rotating Earth-like planets using all three dynamical cores available in CAM. We are currently preparing an accompanying manuscript that focuses on the atmospheric dynamics.

Simulations with our updated radiative transfer (solid line) use the finite-volume dynamical core. These simulations yield similar temperatures under the present-day Earth stellar flux. However, as the stellar flux is increased, simulations using our updated radiative transfer code increase in temperature much more rapidly. For these control simulations, a runaway greenhouse is clearly diagnosed for stellar fluxes exceeding 1900 Wm⁻² using our updated code; using the native radiative transfer, however, a runaway greenhouse is not found until stellar fluxes exceed 2500 Wm⁻². In our new simulations, substellar clouds are still protective against high stellar fluxes, as first shown by Yang et al. (2013); however, the stronger long-wave and short-wave absorption of our model causes the the inner edge of the HZ to be shifted to lower stellar fluxes. This result comes as no surprise in light of the work of Yang et al. (2016) and the results shown here in Figure 1.

We next conduct a suite of simulations for ocean-covered planets around late K and M dwarf stars with effective temperatures of 2600, 3000, 3300, 3700, 4000, and 4500 K. Note that the 2600 K star is roughly the same temperature as TRAPPIST-1, while Proxima Centauri is about 3000 K. Our primary purpose for these numerical experiments is to determine the inner edge of the HZ for both runaway and moist greenhouse limitations. For each simulation set, we study climates with mean surface temperatures (T_s) that range from ∼255 K up to the triggering of a runaway greenhouse, characterized by uncontrolled warming (see Section 3.3 for more details). The stellar flux and planetary rotation rate are self-consistently calculated for each case following Section 2.3. Our results are summarized in Figures 3 and 4.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figure 3(a) shows the global mean surface temperature for each simulation versus the relative stellar flux (i.e., the ratio of the incident stellar flux on the planet to that received by Earth currently, 1360 W m⁻²). All climatologically stable simulations are shown as points connected by solid lines labeled for each given host star. Dashed lines extending upward indicate where a runaway greenhouse is triggered and climate warms uncontrollably despite only a small additional stellar forcing. Similarly, Figure 4(a) shows T_s as a function of the orbital period of the planets. Recall that the orbital period and incident stellar flux are inextricably linked through the mass and luminosity of the host star (Kopparapu et al. 2016). Furthermore, the orbital period equals the rotational period of the planet for synchronous rotators, as are simulated here. Orbital periods for planets near the inner edge of the HZ are proportional to the effective temperature of the star and range from ∼80–100 days around a 4500 K star to only ∼4 days around a 2600 K star. Our work suggests that TRAPPSIT-1 d, which receives about 1.1 times current Earth flux, and whose orbital period is about 4 days, is likely in a runaway greenhouse state.

Our results also agree with Leconte et al. (2013a), who simulated synchronously rotating water-limited planets. If water is readily available on their surfaces, planet Gl 581c, at 2.5 $S/{S}_{0}$ around a ∼3480 K star, and planet HD 85512 b, at 1.85 $S/{S}_{0}$ around a 4715 K star, have both likely undergone a runaway greenhouse.

The consistent shift in the simulated planet curves toward the lower incident flux as we go to cooler stars arises mainly as a result of (1) the shift in the stellar energy distribution toward the red part of the spectrum, where water vapor is a strong absorber (hence, a water-vapor rich planet around a cooler star does not need larger incident flux to quickly warm and transition to a moist or runaway greenhouse regime), and (2) the fact that the rotational periods of planets are shorter around M dwarf stars compared to K dwarfs, resulting in less efficient substellar cloud albedo, which warms the planet at lower incident fluxes.

Figures 3(b) and 4(b) show the stratospheric water-vapor volume mixing ratio as a function of relative stellar flux and orbital period, respectively. Stratospheric ${{\rm{H}}}_{2}{\rm{O}}$ is taken here as the value at the top of the model (1 mbar pressure). The horizontal blue line in Figures 3(b) and 4(b) indicates the classical "moist greenhouse" or water-loss limit to planetary habitability, used by Kasting et al. (1993) and Kopparapu et al. (2013). This assumes that the total planetary ${{\rm{H}}}_{2}{\rm{O}}$ inventory is equal to the amount of water in Earth's oceans currently: $1.4\times {10}^{24}$ g of ${{\rm{H}}}_{2}{\rm{O}}$. This equals $2\times {10}^{28}$ atoms cm⁻². Water vapor that reaches the stratosphere is then photolyzed, releasing hydrogen, which escapes to space, thus irreversibly removing water from the planet. If one assumes that escape is diffusion limited (Hunten 1973), then the timescale for the loss of 1 Earth ocean approaches the current age of Earth when the stratospheric water-vapor volume mixing ratio is $\sim 3\times {10}^{-3}$ (Kasting et al. 1993; Kopparapu et al. 2013). This is the classical criterion of a moist greenhouse climate.

Perhaps the most interesting result evident from Figures 3 and 4 is that conditions necessary for both significant water loss and the triggering of a runaway greenhouse occur at relatively low T_s. The warmest stable climate against a runaway greenhouse is ∼310 K, found for a planet around a 3700 K star, and it is only ∼280 K for planets around a 3000 K star. Furthermore, moist greenhouse conditions become evident at mean surface temperatures as low as ∼280 K. Slow and synchronous rotators can have relatively large amounts of water in their atmospheres for a given T_s owing to strong and persistent deep convection on the substellar hemisphere that continuously lofts water vapor high into the atmosphere. Thus, terrestrial planets may lose their water to space while remaining relatively cool. This is in sharp contrast to simulations of Earth around the Sun, where water-loss conditions are not typically found until ${T}_{s}\gt 350\,{\rm{K}}$ (Wolf & Toon 2015; Popp et al. 2016). Temperatures this warm, while able to support liquid surface water and extremophile life, could not support human biology (Sherwood & Huber 2010). However, in this study, synchronously rotating planets around low-mass stars reach the moist greenhouse threshold (water-vapor mixing ratio $\sim {10}^{-3}$ for 1 bar background N₂ atmosphere) while maintaining robustly habitable surface conditions. A recent paper by Fuji et al. (2017) obtains a similar result using a different GCM (ROCKE-3D; Way et al. 2017), broadly consistent with our results. Note that stable moist greenhouse climates are only possible for planets orbiting host stars with ${T}_{\mathrm{eff}}\geqslant 3300$ K. Planets around 3000 and 2600 K stars, similar to Proxima Centauri and TRAPPIST-1, bypass a water-loss phase and proceed directly to a thermal runaway, for a 1 bar background N₂ atmosphere.

The low surface temperatures for the moist greenhouse regime found in this study raise unexpected and interesting prospects for planets near the inner edge of the HZ around low-mass stars. Low-mass stars may support habitable moist greenhouse worlds that could persist for several billion years during the water-loss process before becoming desiccated. Figure 5 shows the timescale to lose 1 Earth ocean of water, calculated for each simulation based on diffusion-limited escape rates. For 4500, 4000, 3700, and 3300 K stars, ocean-loss timescales can be $\gt 1\,\mathrm{Gyr}$ for stable climates near the inner edge of the HZ. This opens the intriguing possibility that such worlds could transition from water worlds to dry planets while surface temperatures continuously remain within habitable ranges (Kodama et al. 2015). Ocean-loss timescales from stable climates around 3000 and 2600 K stars remain greater than 10 and 100 Gyr, respectively. Around any given star, once a runaway greenhouse instability is triggered, temperatures and thus atmospheric water vapor increase uncontrollably. Then water would be lost from the planet in only a few million years, and the surface would be sterilized.

Zoom In Zoom Out Reset image size

In our simulations we can definitively identify the triggering of a runaway greenhouse. Figure 6 shows time series of temperature, planetary albedo, and the top-of-atmosphere (TOA) energy balance for several stable simulations and for one simulation that enters a runaway greenhouse. While numerical limitations of the model prevent us from exploring the end state of the runway process where ${T}_{s}\sim 1600\,{\rm{K}}$ (Goldblatt et al. 2013), still we can mark where the energy imbalance grows large and temperatures begin to rise uncontrollably. This is sufficient for constraining the inner edge of the HZ for these worlds. Figure 6 shows time series model outputs only for simulations around a 3700 K star; however, a similar temporal evolution is found for each stellar type studied here. In this case, climatologically stable simulations maintain a planetary albedo of ∼0.45, and the TOA energy balance naturally approaches zero. The runaway simulation experiences a collapse of the planetary albedo (dropping to ∼0.1), coincident with a ballooning of the TOA energy balance. At the time of model termination, the global mean surface temperature exceeds 350 K, the maximum atmosphere temperature exceeds 400 K, and the TOA energy imbalance has risen to nearly +150 Wm⁻².

Zoom In Zoom Out Reset image size

For synchronously rotating planets around low-mass stars, the triggering of a runaway greenhouse is intimately linked to the thick substellar cloud deck. Figure 7 illustrates the time evolution of the vertical temperature structure and vertical cloud fraction of the atmosphere at the substellar point during the beginning stages of an ensuing runaway greenhouse. The results in Figure 7 correspond to the runaway greenhouse case also shown in Figure 6.

Zoom In Zoom Out Reset image size

In the opening (Earth) years of simulation, the runaway case maintains thick clouds at the substellar point (Figure 7(b)) while the planetary albedo remains large (Figure 6(b)), similar to the stable cases. However, as temperatures continue to warm, a radiative-convective transition occurs in the low atmosphere. As described by Wolf & Toon (2015), increasing water vapor in the atmosphere for warming climates causes the low atmosphere to become opaque to thermal radiation, while absorption of incident stellar radiation increases. In total, this causes net radiative heating of the low atmosphere, which forms a strong temperature inversion (Figure 7(a)). The inversion encompasses the entire planet, including the substellar point, and stabilizes the low atmosphere against convection. Inversion layers (such as Earth's stratosphere) are inherently stable against vertical mixing. Without deep convection carrying moisture up from the boundary layer, the once thick and highly reflective, convectively produced substellar cloud deck dissipates completely. High temperatures within the inversion layer led to low relative humidities and clear skies, despite a considerable water-vapor burden. In the absence of these substellar clouds, the planetary albedo plummets and the planet is left unprotected against large stellar fluxes. The energy imbalance skyrockets, and a thermal runaway becomes inevitable.

The climates of planets in the HZs of low-mass stars are inextricably controlled by the nature of the host star. The orbital period, total incident stellar flux, and stellar energy distribution are all correlated, determined by the mass and luminosity of the host star. Higher-mass stars are bluer and brighter, and thus planets in their HZ must reside at further distances and thus will have longer periods and slower rotation rates. Here we find that planets near the inner edge of the HZ around 4500 K stars will have periods of ∼80–100 Earth days (Figure 4). Lower-mass stars are redder and dimmer; thus, HZ planets must remain closer to their host star and on shorter periods. For instance, near the inner edge of the HZ planets around a 2600 K star have orbital periods of only ∼4–5 days (Figure 4). Differences in the rotation rate of these planets are of critical importance, because the rotation rate of the planet imposes a strong control on the atmospheric circulation regime through the modulation of the Coriolis force. Slow rotation weakens the Coriolis effect and causes the atmospheric circulation to shift from a "rapidly rotating" regime characterized by zonal uniformity and symmetry about the equator (e.g., like Earth currently) to a "slow-rotating" regime characterized by dayside to nightside transport and circular symmetry about the substellar point. The transition between these circulation regimes occurs when the rotation rate exceeds ∼5 days for a 1 R_⊕ planet (Yang et al. 2014). Thus, planets near the inner edge of the HZ around a 2600 K star with a ∼4-day rotation rate (like TRAPPIST-1d) should be in the fast-rotating circulation regime. Planets near the inner edge of the HZ around 3000 K star have rotations rates of ∼8 days and thus may represent a transitional state between rapid and slow rotators. All other cases studied lie firmly within the slow-rotating regime. The circulation regime critically feeds back on the planets' distribution of clouds.

Figure 8 shows contour plots of surface temperature, TOA albedo, integrated cloud water column, and integrated cloud fraction for a present-day Earth control simulation, and then for HZ planets around each of our six low-mass stars studied here. Note that the incident stellar flux on the planet, the planet's rotational period, and the planet's mean surface temperature are listed at the left margin of Figure 8. The white line overplotted on the surface temperature contour indicates the location of the sea-ice margin. The substellar point is located at the center of each panel. All simulations shown in Figure 8 have moderate surface temperatures, with 276 K $\leqslant \,{T}_{s}\leqslant 288$ K. We have chosen to display simulations with similar T_s, because the mean temperature of the planet dictates sea ice and the atmospheric water vapor, both of which impose primary controls on planetary climate. By comparing simulations of nearly the same temperature (despite varying stellar flux, period, and spectra), we can normalize against temperature-dependent feedbacks on climate.

Zoom In Zoom Out Reset image size

The climates shown in Figure 8 are modulated by the rotation rate of each planet, through the feedback between the large-scale circulation and water clouds. The TOA albedo is largely controlled by the fraction and thickness of the clouds. Note that in Figure 8 dark (light) colors represent areas of low (high) albedo for the planets in the second column. The patterns emergent in planetary albedo mirror the distribution of the cloud water column and cloud fraction. Regions of thick and ubiquitous clouds are naturally coincident with regions of high albedo. Fast rotators, like present-day Earth and planets near the inner edge of the HZ around ultra-low-mass stars (i.e., 2600 K in this study), exhibit zonal patterns of temperature and clouds. These climates feature the fewest clouds and the lowest albedos and thus reach Earth-like temperatures at relatively low values of the incident stellar flux. For planets around a 2600 K star, while the overall pattern is zonal, the planet retains the signature of a substellar hot spot owing to its synchronous rotation. Around increasingly higher T_eff stars, the rotational period of HZ planets becomes necessarily longer and the circulation regime shifts. Substellar clouds become increasingly thick and ubiquitous, resulting in higher planetary albedos and larger required incident stellar fluxes to maintain Earth-like temperatures.

The zonal circulation is the predominant circulation pattern on synchronously rotating planets, providing the primary means of energy transport from the substellar to antistellar hemisphere. Figure 9 shows the mean zonal circulation (MZC, also known as the Walker circulation) for planets in synchronous rotation around stars with ${T}_{\mathrm{eff}}=3300$ K and ${T}_{\mathrm{eff}}=2600$ K (top row), as well as in units of pressure tendency. Note that pressure tendency is a commonly used unit for expressing vertical motion in the atmosphere, i.e., a negative pressure tendency refers to rising motion, and vice versa.

Zoom In Zoom Out Reset image size

We note that a planet in a stable 4.25-day orbit near the inner edge of the HZ around a star with ${T}_{\mathrm{eff}}=2600$ K rotates fast enough that the Rossby deformation radius is less than the planetary radius. Thus, while the planet around the ${T}_{\mathrm{eff}}=3300$ K star is able to sustain strong rising motion at the substellar point and a hemisphere-spanning MZC from the dayside to nightside, the planet around the ${T}_{\mathrm{eff}}=2600$ K star lacks a region of strong convection beneath its substellar point and shows a less organized structure than the time-average MZC. Strong convection is also absent in the time-average MZC for the 24 hr rotating planets, where the lack of a fixed substellar point indicates the presence of complex, diurnally varying MZC patterns closer to those observed on Earth today. Differences between the planet orbiting the Sun and Ad Leo are small, with planetary rotation rate being the prevailing factor for predicting differences in atmospheric circulation.

Figure 10(a) shows our simulated model cases around stars with $2600\,{\rm{K}}\leqslant {T}_{\mathrm{eff}}\leqslant 4500\,{\rm{K}}$. The blue-square simulations have mild climates, with low stratospheric ${{\rm{H}}}_{2}{\rm{O}}$, whereas the green squares have TOA water vapor of 10⁻³ or greater ("moist stratosphere"). Red crosses are simulations where the planet is in thermal runaway. For planets in synchronous orbits around stars with ${T}_{\mathrm{eff}}\gt 3000$ K, there is an intermediate stage where the upper atmosphere is dominated by water vapor, before the planet transitions to a runaway with an increase in stellar flux. For stars with ${T}_{\mathrm{eff}}\leqslant 3000\,{\rm{K}}$, the planet directly transitions to a runaway from a stable mild climate. As discussed in previous sections, this abrupt transition to a thermal runaway, without undergoing a water-vapor-dominated atmosphere, arises partly as a result of the shorter orbital periods (and hence faster rotation rates), which advect the persistent substellar cloud deck to the nightside, decreasing the planetary albedo and increasing the surface temperatures. This effect is compounded by the shift in the peak wavelength of the stellar spectra toward the near-IR for low-mass stars, where ${{\rm{H}}}_{2}{\rm{O}}$ vapor is a strong absorber. Our updated absorption coefficients for water vapor further magnify this effect, leading to the runaway greenhouse phase for any further increase in the stellar flux.

Zoom In Zoom Out Reset image size

Figure 10(b) shows our moist and runaway greenhouse limits in comparison with our previous study (Kopparapu et al. 2016) and Yang et al. (2014a). Note that, as with Yang et al. (2014a), Kopparapu et al. (2016) also assumed that the last converged solution represents the IHZ.¹⁰ We assumed a solar metallicity for all the stars in this study. Compared to our previous results, the inner edge of the HZ (either moist or runaway GH) is located at considerably lower stellar fluxes for late K and M dwarf stars. Considering that the global mean surface temperatures at the moist greenhouse limit are ∼280 K, we conclude that, for M dwarf stars, the inner edge of the HZ is identified by the runaway greenhouse limit and moist greenhouse planets around these stars can be habitable, revising decades of previous assumptions about the moist greenhouse.

We remind the reader that our simulations assume a background N₂ atmosphere of 1 bar. Several studies have shown that the variation in the noncondensable gas fraction in the atmosphere (specifically the N₂ amount) can affect the OLR and consequently the habitability limits through moist and runaway greenhouse (Nakajima et al. 1992; Pierrehumbert 2010; Kopparapu et al. 2014; Wordsworth & Pierrehumbert 2014). For a higher N₂ amount in the atmosphere, the surface temperature needs to be higher to radiate the same amount of OLR. The reason for this is that the amount of water-vapor fraction in the atmosphere is not high enough relative to the N₂ fraction. Consequently, planets with higher N₂ can potentially reach moist greenhouse limits at higher temperatures than ∼280 K. Conversely, if there is less than 1 bar ${{\rm{N}}}_{2}$ in the atmosphere, then water loss could occur at even lower temperatures. Still, our assumption of a 1 bar ${{\rm{N}}}_{2}$ atmosphere is in line with previous studies (Kasting et al. 1993; Kopparapu et al. 2013; Leconte et al. 2013b; Yang et al. 2014; Wolf & Toon 2015; Popp et al. 2016). An exploration of the effects of varying ${{\rm{N}}}_{2}$ on moist greenhouse atmospheres in 3D models is left for future parameter studies.

We further remind the reader that differences exists across 3D climate models of varying origin. For example, outcomes for standard anthropogenic climate change scenarios can vary by several kelvin over the next two centuries, depending on the model being used (Rogelj et al. 2012). However, the implied radiative forcings for simulated exoplanets are typically much larger and yield wider spreads in model results (e.g., Popp et al. 2016; Figure 7). Formal model intercomparisons are needed in order to make sense of these model differences.

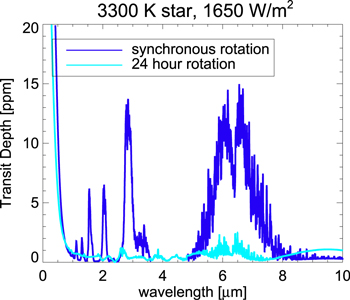
M dwarf planets will be targeted by JWST, and if habitable planets can exist closer to these stars than the traditional HZ boundaries, their shorter orbital periods will allow us to observe them more frequently. For example, the TRAPPIST-1 system has three planets (d, e, and f) in the habitable zone. TRAPPIST-1 is visible for a total of 99 days in JWST's Cycle 1 (STScI APT). Planets d, e, and f have orbital periods of 4, 6, and 9 days, respectively. Therefore, in cycle 1 (1 yr), planet f can be observed for a maximum of 11 transit observations, whereas planet d can be observed for a maximum of 24 transits. TRAPPIST-1 has a stellar effective temperature of 2600 K, so it is not directly applicable to the moist greenhouse atmospheres discussed here. However, it does offer an estimate for what a feasible amount of observing time is for JWST. Therefore, if we use TRAPPIST-1's observability window as a standard estimate, we can calculate the expected noise on the transmission spectra of the planets of interest in this study (moist greenhouse planets around stars with ${T}_{\mathrm{eff}}\gt 3300$ K). In Figure 11, we show a simulated transit transmission spectrum from our GCM simulations, where the planet is undergoing moist greenhouse around an M3 spectral type star with ${T}_{\mathrm{eff}}=3300\,{\rm{K}}$ and stellar radius of 0.137 ${R}_{\oplus }$ (dark blue). All spectra were generated using the SMART model, a versatile line-by-line 1D radiative transfer model (Meadows & Crisp 1996). Transit spectra are generated from GCM results by using atmospheric columns from the planetary terminator region. This planet's atmosphere includes ${{\rm{N}}}_{2}$ as the background gas with stratospheric ${{\rm{H}}}_{2}{\rm{O}}$ volume mixing ratio of 10⁻³ (see Figures 3 and 4) and self-consistent liquid and ice water clouds. Figure 11 shows that for a habitable moist greenhouse planet, there are two prominent water-vapor features, including one between 5 and 8 μm, within the JWST MIRI LRS (Mid Infra-Red Instrument Low Resolution Spectrometer) bandpass, and another between 2.5 and 3 μm, within the NIRCam grism with the F322W2 filter and the NIRSpec G235M/H bandpasses. These features, caused by a wet upper atmosphere, are a direct consequence of the strong and persistent convection that occurs at the substellar region for slowly rotating planets. This strong substellar convection is effective at pumping water vapor into the high atmosphere.

Zoom In Zoom Out Reset image size

In Figure 11, we also show a planet simulated around an M dwarf, but with a standard 24 hr rotation period (light-blue spectrum). Previous studies of Earth-analog spectra for planets in the HZ around M dwarfs have not included the impact of synchronous rotation (Barstow et al. 2015; Schwieterman et al. 2016). Taking into account the effect of M dwarf rotation on cloud and species distributions will be crucial to accurately model the spectra of these worlds. Note how the planet simulated with a 24 hr rotation period results in a dramatically different spectrum in Figure 11 compared to including synchronous rotation. The water-vapor spectral feature is ∼7 times weaker in the atmosphere of the planet with the 24 hr rotation period because the strong substellar convection is absent.

Despite the increased strength of the water absorption with the inclusion of synchronous rotation, the two strongest water spectral features in Figure 11 are well below the postulated JWST noise floor of 20 and 50 ppm for the near-IR and mid-IR instruments aboard JWST (Greene et al. 2016). In reality, though, noise floors will not prevent observations of potentially habitable systems, and the true noise floor of JWST remains to be determined. For example, TRAPPIST-1 is a compelling enough target that it is already on JWST's Guaranteed Time Observer's plan. If other compelling small planets are found (planets that may fit the planet type described here), they may end up being observed, and so we should address what, if anything, we could learn from their transmission spectra.

Assuming that JWST encounters no systematic noise floor (which is unlikely), we can calculate how many observing hours would be needed to obtain sub-10 ppm precision. Noise floors are created when instrument systematics cannot be removed from co-adding transits. Therefore, they create a minimum level equal to the strength of the systematic effect. Figure 12 shows the approximate error on the spectrum of an MIRI observation at 6 μm for a range of stellar brightnesses (2MASS J), without any inclusion of a systematic noise floor. We chose the MIRI band because of the broadness of the $6\,\mu {\rm{m}}$ water feature and because, as we are not including any systematic noise floor and observing an M3 star, the noise calculations are similar if the near-IR simulations are binned to R = 100. These calculations were performed using JWST's publicly available noise simulator, PandExo (Batalha et al. 2017), for the same planet system shown in Figure 11. Assuming an observability window comparable to TRAPPIST-1 and an inner edge planet, the planet system would need to be observed through the entirety of Cycle 1 (24 transits) to reach the approximate strength of the water feature.

Zoom In Zoom Out Reset image size

Solely surpassing the strength of the water feature would yield a confirmation of the presence of water, not necessarily a constraint on the water abundance. In this particular scenario (aquaplanet, no land), if the presence of water is confirmed, one could say that the planet is in either a moist greenhouse or a habitable state given its stellar type and orbital period (see Figure 4). If the system was then observed through Cycles ∼2–3 (∼60 transits), a traditional Bayesian retrieval might be possible to constrain the water mixing ratio and corresponding temperature (such as that done in Barstow et al. 2016). Barstow et al. (2016) estimate retrieved errors on water abundance on the order of ±1 dex in mixing ratio. If it is possible to measure the water content to a level of precision of approximately ±1 dex, there would be three potential scenarios in accordance with Figure 4 (habitable, entering moist greenhouse, in moist greenhouse). Since transmission spectra will not probe the surface of terrestrial planets, we can use Figure 4 to predict a surface temperature. This would require constraints on the stratospheric temperature, the water mixing ratio, and information on the stellar type and orbital period.

In a scenario where by the end of Cycle 3 there is still no detection of any water spectral features, two possibilities exist: either the planet is a fast rotator so that strong substellar convection is absent, or the planet is dry. Both scenarios would be astrophysically interesting. Of course, there are other factors, which may complicate this simple qualitative view of exoplanet characterization. For example, here we have assumed an aquaplanet with no land. The effect of adding continents may also result in reduced ${{\rm{H}}}_{2}{\rm{O}}$ features. An exploration of these dependencies is left as future work.