子ども達にB5用紙を渡し、投げかけます。
※長方形であれば、他のサイズでもOK。(試し刷りの反古紙は要注意です。)



紙を折って、対角線をつくってみてください。
対角線を引いてから折る、なんてのはダメです。できるかな?
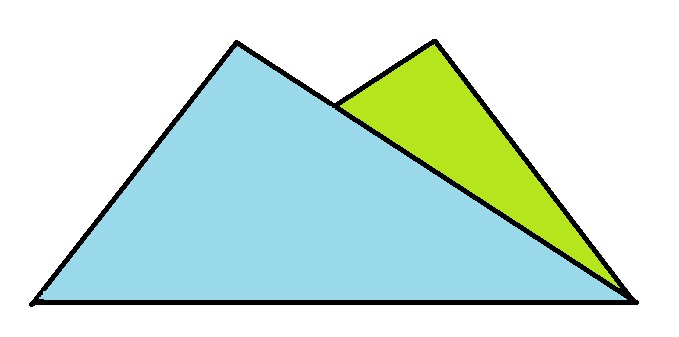
恐らく、右図のようにすると思われます。
これを開けば、折り目が対角線になっているはずです。
これが、なかなかうまくいきません。
折り目と頂点と合わせるので一苦労です。
ずれてしまいます。

うまい折り方があるので以下、ご紹介します。
先生方の授業づくりのお役に立てたら幸いです。
※この学習活動について知ったのは、
研数学館が開催する「算数・数学講演会」でのことで、2011年~2015年の頃だったと思います。
毎回、算数・数学の授業づくりに大変役立つお話をいただきました。
この場をお借りして感謝申し上げます。
研数学館のセミナーはこちら 一般財団法人 研数学館 (kensu.or.jp)
折り方
「対角線」は、小学校の4年生で習います。
5年になると、「対角線で分けた三角形の合同」について学習します。
その頃にこの活動をしてみるといいかもしれません。
それでは、折り方です。


長方形ABCDの頂点Cをつまんで、頂点Aと重ねます。
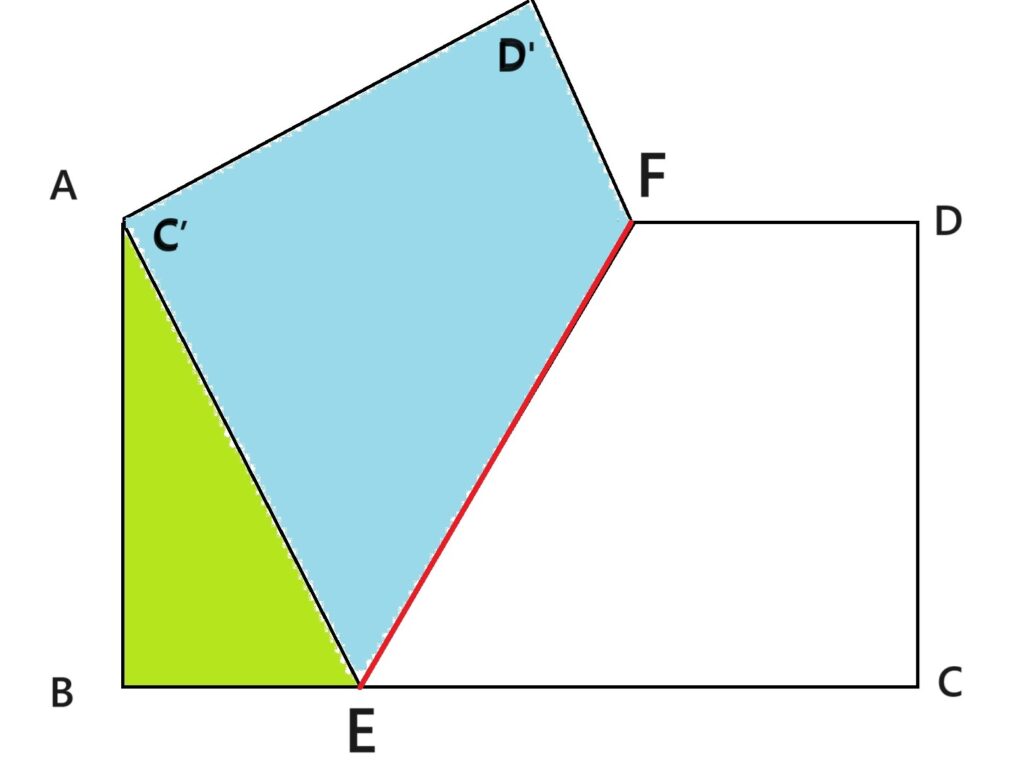

EF(赤い線)を折り目として・・・
次に、D’をつまんでBに重ねます。(FもEと重なります。)
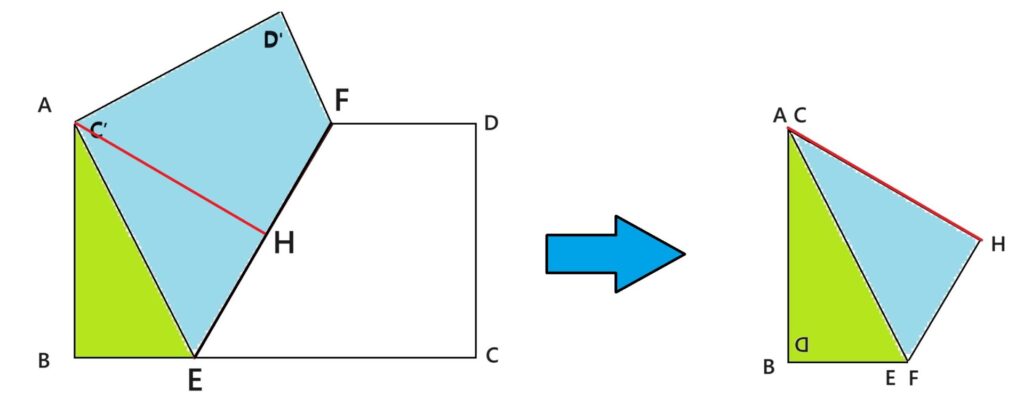

長方形の辺ABは辺CDと重なります。
(AB=CD)
FはEと重なっています。(前述)
折るのは、ここでおしまい。
AH(CH)が目的の折り目です。
これを開くと、折り目が2つ出来ています。(右図)
そのうちの1本が対角線です。
向かいあった頂点を結んでいる直線です。
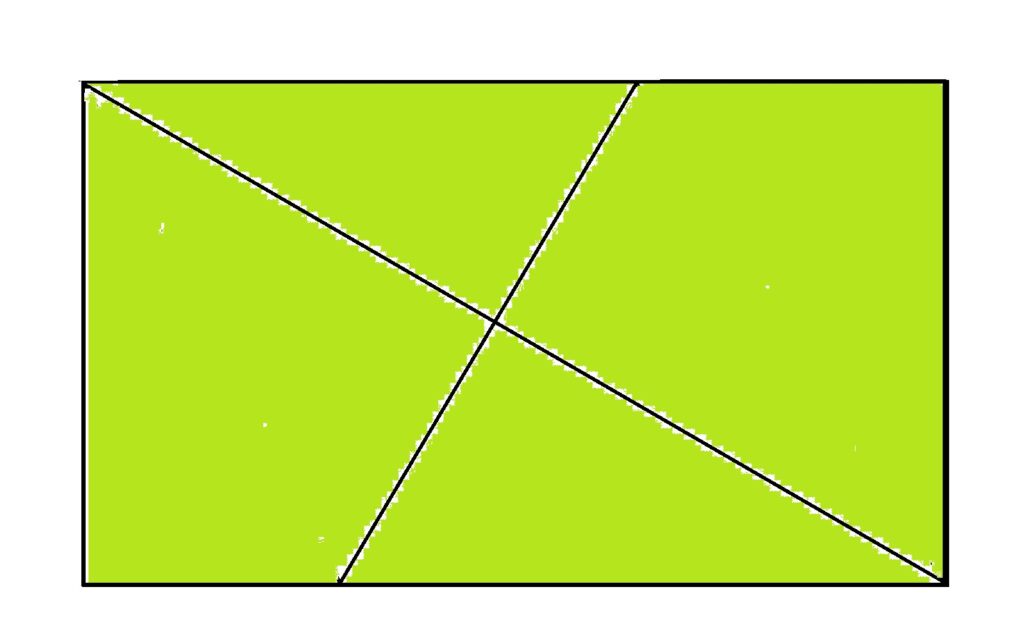

長方形の紙を2回折って対角線をつくることができました。
授業で
その仕方を教えるだけでは、単なる作業で終わってしまいます。
そこで、授業にしてみます。
案1 対角線の定義を確認する
折り方を教え、
開かせたところで、子ども達に投げかけます。



対角線が2本できていた人! (手を挙げてごらん)
ほとんどの子どもが手を挙げるのではないかと思われます。
実際に授業をしてみないと分かりませんが、
対角線を初めて習ったばかりの4年生だと恐らくひっかかります。(しめしめ、です。)
中には、「対角線は1本だよ。もう一本は違うよ。」という子どもがいるかもしれません。
それを説明させる場面がつくれそうです。
「対角線」とは、向かいあった頂点を結ぶ直線のことです。
折り目を「直線」とみなせば、この方法で折ってできた対角線は1本です。
「折り目は直線ではない」
そういう話になると、対角線は1本もできていないことになります。
では「直線」とは何なのか?
「そのことは中学高校で学びますよ。楽しみだね。」と言っておきます。
4,5年生で、そこまで拘る子どもはいないと思われますが。
案2 平行四辺形・ひし形の学習へ
対角線ができる折り方を教えます。(前述のとおりです。)
開かせ、折り目を鉛筆でなぞらせます。
もちろん、
フリーハンドではありません。定規を使わせます。(A図)
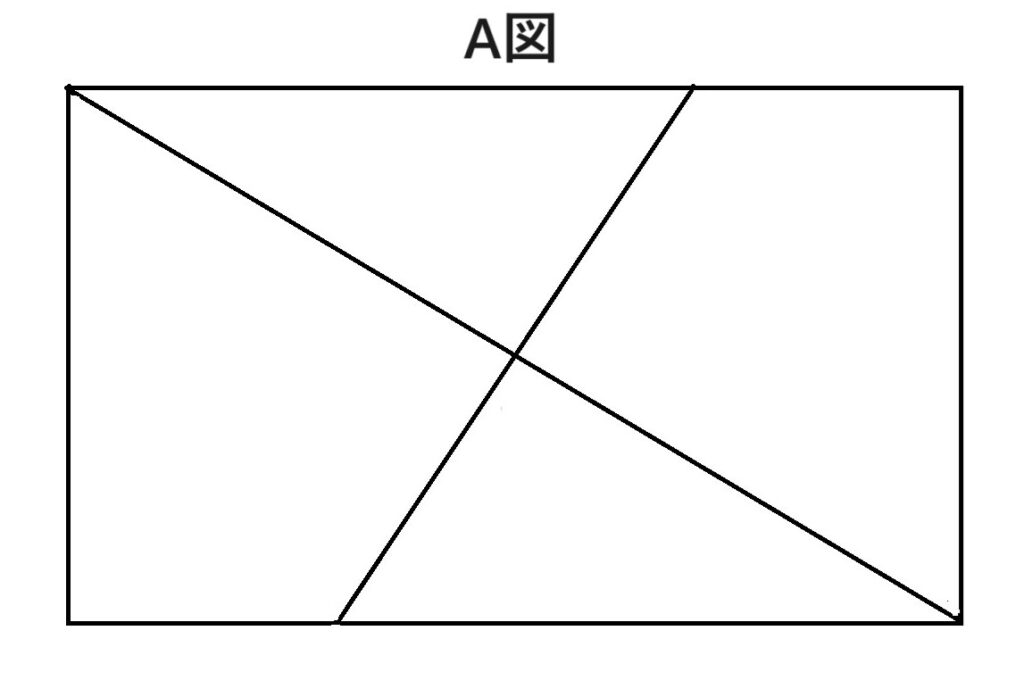

そこで投げかけます。



折り目で線を引きました。「ある四角形」が見えてきましたね?
と言ってもぴんとこない、かもしれません。
ヒントを出します。



この2つの折り目が「ある四角形」の対角線になっていますよ。
平行四辺形です。
少し学習が進んでいれば、「ひし形」と答える子どもがいるかもしれません。
よく気が付いたね、とおおいに褒めます。
授業は、そっち(ひし形)へ行ってはいけません。
T:まず、書き足して平行四辺形にしてみましょう。
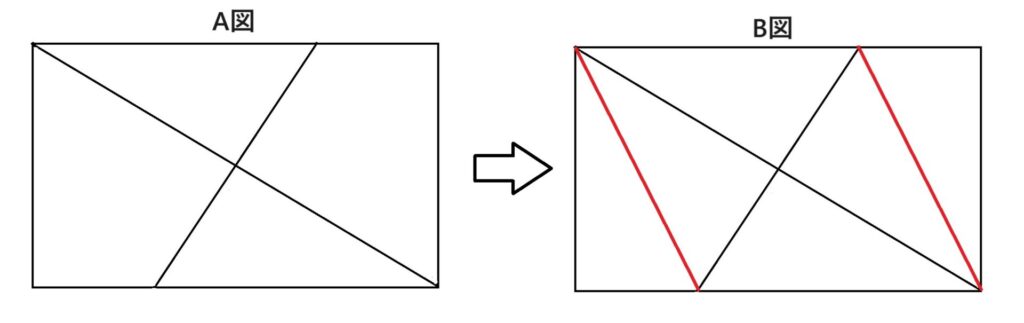

直線を引かせます。(B図 赤線)
そこで、発問。



これは「平行四辺形」ですよね。
その理由をお隣さんに説明しましょう。
じゃんけんで負けた人から言いましょうか。
じゃんけんで負けた人から説明する。
これは、ペア学習でよく使う手法です。
この授業技術が有効なのは、
子ども達のほとんどが説明できると見込める場合だけです。
さもなければ、時間の無駄です。


説明できる子どもが少ないと思える場合は、どうするか?
まずは、その場で実態を把握します。



全員起立!
これは「平行四辺形」ですよね。
その理由を説明できる人は、座りましょう。
座った子どもを数人指名して説明させます。前に出てきてやってもらいます。
必ず、数人にさせます。
T:立っている人! 説明できそうだと思ったら座っていきましょうね。
この指示で、子ども達は追い込まれます。
周りが次々に座り出すと、焦ります。友達の説明を全身を耳にして聞くでしょう。
それでも、
立ち続ける子どもがいます。自分に正直な子どもは、座りません。
そこをいっぱい褒めてから座らせます。
誤魔化して座っちゃう子どももいるとは思いますが、にこにこと笑顔を送ります。
この流れで、
平行四辺形であることを説明できる子どもは、増えているはずです。
そこで、先に述べたペア学習に移ります。
説明しあうようにさせます。
なぜ説明し合う場面を設定するのか?
論理的に説明できる力を(どの子にも)つけさせたいからです。
ちなみに、
友達の説明がよいと思ったら褒めてあげましょう、と言います。
説明が不十分だったら、Helpしてあげましょう、と言います。
課題に取り組むどうしでのコミュ力を育むためです。
平行四辺形になっていることの説明
子ども達はどのように説明するでしょうか。
平行四辺形の定義は、「2組の向かい合った辺が平行」というものですが、
それを説明することは少々難しいと思われます。
そこで、おさらいをします。手がかりを与えます。



長方形って、どんな四角形だっけ?
辺AFと辺ECが平行であることに子ども達は気付くはずです。
長方形ABCDの一部ですから、向かい合ったこの2辺は平行です。
「辺AEと辺FCが平行である」ことの説明は、どうでしょうか。
角AEBと角FCE(角CFD)の角の大きさが等しいことを言えればOKとしましょうか。
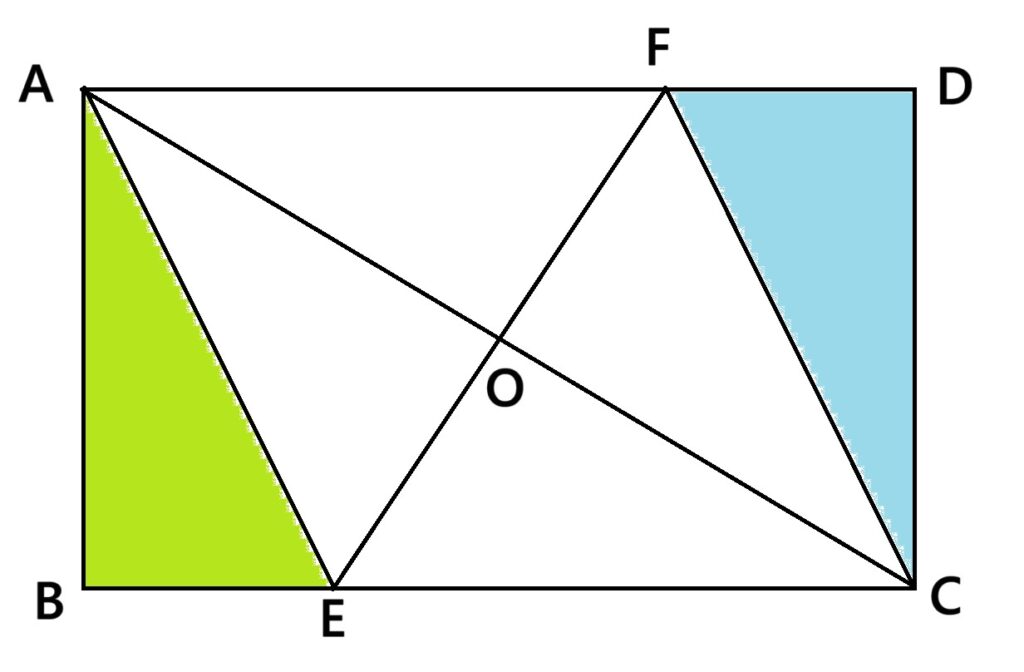

△ABEと△CDFが合同であることは、
合同条件から説明できますが、子どもの半分は聞いていないでしょう。
手っ取り早いのは、折ってみることです。
色を塗らせ、折らせるのです。
ぴたりと重なります。
2つの三角形は合同です。
辺ADと辺BCは平行ですから、角AEB=角DFC=角FCE。
よって辺AEと辺FCは平行です。
平行四辺形の性質(定理)を挙げる子どももいると思います。
その説明は、一度ノートに書かせてから発表させるといいかもしれません。

