ANOVA Test, or Analysis of Variance, is a statistical method used to test the differences between means of two or more groups. Developed by Ronald Fisher in the early 20th century, ANOVA helps determine whether there are any statistically significant differences between the means of three or more independent groups.
The ANOVA analysis is a statistical relevance tool designed to evaluate whether or not the null hypothesis can be rejected while testing hypotheses. It is used to determine whether or not the means of three or more groups are equal.
The ANOVA test is used to look for heterogeneity within groups as well as variability across groupings. The f test returns the ANOVA test statistic.
ANOVA formula is made up of numerous parts. The best way to tackle an ANOVA test problem is to organize the formulae inside an ANOVA table. Below are the ANOVA formulae.
Source of Variation
| Sum of Squares
| Degree of Freedom
| Mean Squares
| F Value
|
|---|
| Between Groups | SSB = Σnj(X̄j– X̄)2 | df1 = k – 1 | MSB = SSB / (k – 1) | f = MSB / MSE
or, F = MST/MSE
|
| Error | SSE = Σnj(X̄- X̄j)2 | df2 = N – k | MSE = SSE / (N – k) | |
| Total | SST = SSB + SSE | df3 = N – 1 | | |
where,
- F = ANOVA Coefficient
- MSB = Mean of the total of squares between groupings
- MSW = Mean total of squares within groupings
- MSE = Mean sum of squares due to error
- SST = total Sum of squares
- p = Total number of populations
- n = The total number of samples in a population
- SSW = Sum of squares within the groups
- SSB = Sum of squares between the groups
- SSE = Sum of squares due to error
- s = Standard deviation of the samples
- N = Total number of observations
- Assume it is necessary to assess whether consuming a specific type of tea will result in a mean weight decrease. Allow three groups to use three different varieties of tea: green tea, Earl Grey tea, and Jasmine tea. Thus, the ANOVA test (one way) will be utilized to examine if there was any mean weight decrease displayed by a certain group.
- Assume a poll was undertaken to see if there is a relationship between salary and gender and stress levels during job interviews. A two-way ANOVA will be utilized to carry out such a test.
ANOVA Table
An ANOVA (Analysis of Variance) test table is used to summarize the results of an ANOVA test, which is used to determine if there are any statistically significant differences between the means of three or more independent groups. Here’s a general structure of an ANOVA table:
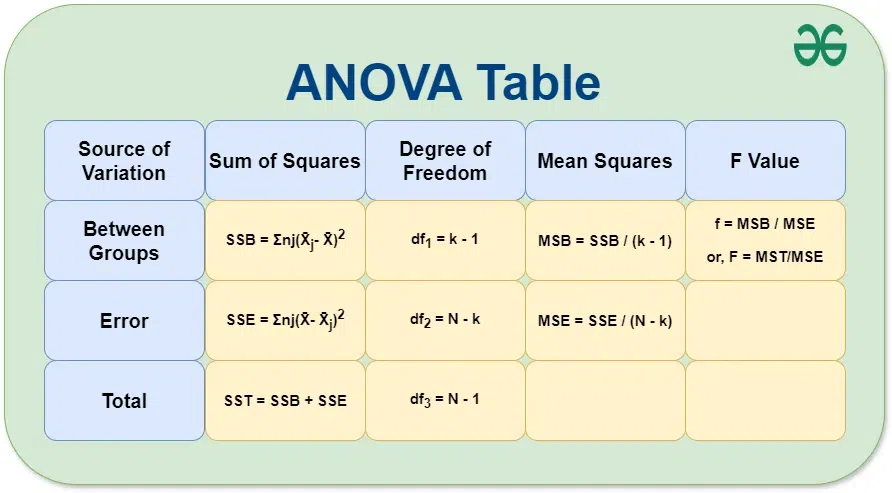
ANOVA Table
One-Way ANOVA
This test is used to see if there is a variation in the mean values of three or more groups. Such a test is used where the data set has only one independent variable. If the test statistic exceeds the critical value, the null hypothesis is rejected, and the averages of at least two different groups are significant statistically.
Two-Way ANOVA
Two independent variables are used in the two-way ANOVA. As a result, it can be viewed as an extension of a one-way ANOVA in which only one variable influences the dependent variable. A two-way ANOVA test is used to determine the main effect of each independent variable and whether there is an interaction effect. Each factor is examined independently to determine the main effect, as in a one-way ANOVA. Furthermore, all components are analyzed at the same time to test the interaction impact.
Example 1: Three different kinds of food are tested on three groups of rats for 5 weeks. The objective is to check the difference in mean weight(in grams) of the rats per week. Apply one-way ANOVA using a 0.05 significance level to the following data:
| Food I | Food II | Food III |
|---|
| 8 | 4 | 11 |
| 12 | 5 | 8 |
| 19 | 4 | 7 |
| 8 | 6 | 13 |
| 6 | 9 | 7 |
| 11 | 7 | 9 |
Solution:
H0: μ1= μ2=μ3
H1: The means are not equal
Since, X̄1 = 5, X̄2 = 9, X̄3 = 10
Total mean = X̄ = 8
SSB = 6(5 – 8)2 + 6(9 – 8)2 + 6(10 – 8)2 = 84
SSE = 68
MSB = SSB/df1 = 42
MSE = SSE/df2 = 4.53
f = MSB/MSE = 42/4.53 = 9.33
Since f > F, the null hypothesis stands rejected.
Example 2: Calculate the ANOVA coefficient for the following data:
| Plant | Number | Average span | s |
|---|
| Hibiscus | 5 | 12 | 2 |
| Marigold | 5 | 16 | 1 |
| Rose | 5 | 20 | 4 |
Solution:
| Plant | n | x | s | s2 |
|---|
| Hibiscus | 5 | 12 | 2 | 4 |
| Marigold | 5 | 16 | 1 | 1 |
| Rose | 5 | 20 | 4 | 16 |
p = 3
n = 5
N = 15
x̄ = 16
SST = Σn(x−x̄)2
SST= 5(12 − 16)2 + 5(16 − 16)2 + 11(20 − 16)2 = 160
MST = SST/p-1 = 160/3-1 = 80
SSE = ∑ (n−1) = 4 (4 + 1) + 4(16) = 84
MSE = 7
F = MST/MSE = 80/7
F = 11.429
Example 3: The following data show the number of worms quarantined from the GI areas of four groups of muskrats in a carbon tetrachloride anthelmintic study. Conduct a two-way ANOVA test.
| I | II | III | IV |
|---|
| 338 | 412 | 124 | 389 |
| 324 | 387 | 353 | 432 |
| 268 | 400 | 469 | 255 |
| 147 | 233 | 222 | 133 |
| 309 | 212 | 111 | 265 |
Solution:
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square |
|---|
| Between the groups | 62111.6 | 8 | 9078.067 |
| Within the groups | 98787.8 | 16 | 4567.89 |
| Total | 167771.4 | 24 | |
Since F = MST / MSE
= 9.4062 / 3.66
F = 2.57
Example 4: Enlist the results in APA format after performing ANOVA on the following data set:
[Tex]\begin{bmatrix} \textbf{n} & \textbf{mean} & \textbf{sd} \\ 30 & 50.26 & 10.45 \\ 30 & 45.32 & 12.76 \\ 30 & 53.67 & 11.47 \\ \end{bmatrix}
[/Tex]
Solution:
Variance of first set = (10.45)2 = 109.2
Variance of second set = (12.76)2 = 162.82
Variance of third set = (11.47)2 = 131.56
MSerror = {109.2 + 162.82 + 131.56} / {3}
= 134.53
MSbetween = (17.62)(30) = 528.75
F = MSbetween / MSerror
= 528.75 / 134.53
F = 4.86
APA writeup: F(2, 87)=3.93, p >=0.01, η2=0.08.
Articles Related to ANOVA Formula:
Conclusions
ANOVA formula is an important tool for anyone involved in statistical analysis or research. It provides a robust method for comparing the means of multiple groups and determining whether observed differences are statistically significant. By breaking down the total variance into components attributable to various factors and within-group variation, ANOVA helps to identify whether these differences are due to random chance or actual effects. Mastery of the ANOVA formula enables more precise and reliable conclusions.
How does one set the hypothesis for ANOVA?
The equality of the means of distinct groups must be tested in an ANOVA test. As a result, the hypothesis is as follows:
- H0 = 1 = 2 = 3 =… = k = Null Hypothesis
- H1 is Alternative Hypothesis: The means are not equal.
How do you calculate the ANOVA?
ANOVA compares group means’ differences. Calculate Grand Mean, Between-Group Variability (SSB), and Within-Group Variability (SSW). Determine significance through variance comparison.
What is meant by ANOVA statistic?
The sample mean of the jth treatment of a grouping or a mass data sample is called the ANOVA statistic. It is denoted by the alphabet f.
What is the p value in ANOVA?
In ANOVA, a shared P-value is initially obtained. A significant P-value in the ANOVA test suggests statistical significance in at least one pair’s mean difference. Multiple comparisons are then employed to identify these significant pair(s).
What do you mean by one-way ANOVA?
One-way ANOVA is a form of ANOVA test that is used when just one independent variable is present. It compares the means of the various test groups. A test of this type can only provide information on the statistical significance of the means; it cannot establish which groups have different means.
What is accuracy of the ANOVA test?
Since it is more versatile and requires fewer observations, ANOVA analysis is sometimes thought to be more accurate than t-testing. It is also more suited to employ in more sophisticated studies than those that can be evaluated by testing.