Cauchy’s Mean Value Theorem

Cauchy’s Mean Value theorem provides a relation between the change of two functions over a fixed interval with their derivative. Cauchy Mean Value Theorem is a special case of Lagrange Mean Value Theorem. Cauchy’s Mean Value theorem is also called the Extended Mean Value Theorem or the Second Mean Value Theorem.

In this article, we will learn about Cauchy’s Mean Value Theorem, its proof, some examples based on Cauchy’s Mean Value Theorem, and others in detail.

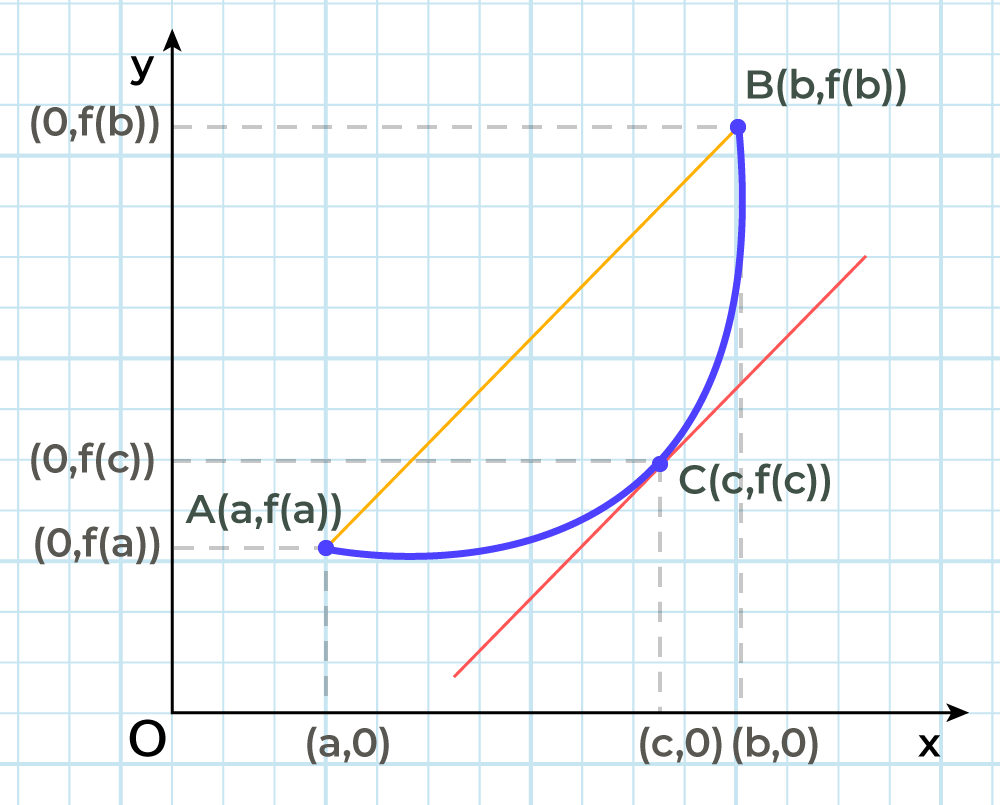
What is Mean Value Theorem?

According to the Mean Value Theorem, if a function passes through two points given as [a, f(a)] and [b, f(b)] then there exist a point through which tangent on the curve passes which is parallel to the secant passing through the two given points.

For the function f(x) continuous over [a, b] and differentiable over (a, b), there exists a point c in the interval (a, b) such that

[Tex]f'(c) = \frac{[f(b) – f(a)]}{(b – a)}[/Tex]

The image for Mean Value Theorem is added below:

Cauchy’s Mean Value Theorem

Statement

Cauchy’s Mean Value Theorem states that, for any two functions, f(x) and g(x) satisfying the following conditions,

• f(x), g(x) are continuous in the closed interval a ≤ x ≤ b, x ϵ [a, b]
• f(x), g(x) are differentiable in the open interval a < x < b, i.e. x ϵ (a, b)
• [Tex]g'(x) \ne0[/Tex] for all x belongs to the open interval a < x < b, i.e. x ϵ (a, b)

Then there exists a point c in the open interval a < c < b such that,

[Tex]\frac{[f(b) – f(a)]}{ [g(b) – g(a)]}= \frac{f'(c)}{g'(c)}[/Tex]

Read in Detail: Calculus in Maths

Proof of Cauchy’s Mean Value Theorem

Cauchy’s mean value theorem is easily proved using the Rolle’s Mean Value Theorem. Cauchy’s mean value theorem states that, for any two function f(x) and g(x) continuous on [a, b] and differentiable on (a, b) there exist a point in the interval (a, b) such that,

[Tex]\frac{f'(c) }{g'(c)} = \frac{[f(b) – f(a)]}{ [g(b) – g(a)]}[/Tex]

Now, let’s take the auxiliary function F(x) such that,

F(x) = f(x) + P×g(x)…(i)

In the above equation, P is chosen such that F(x) always satisfies the Rolle’s Theorem in [a, b], Now by definition of Rolle’s theorem,

F(a) = F(b)

⇒ f(a) + P×g(a) = f(b) + P×g(b)

⇒ f(b) – f(a) = P{g(b) – g(a)}

⇒ [Tex]P = \frac{[f(b) – f(a)]}{[g(b) – g(a)]}[/Tex]

In eq.(i)

[Tex]F'(x) = f'(x) – {\frac{[f(b) – f(a)]}{[g(b) – g(a)]}}×g'(x)[/Tex]

As, F(x) satisfies Rolles Theorem, F(c) = 0 where, c ϵ (a, b)

⇒[Tex] f'(c) – {\frac{[f(b) – f(a)]}{[g(b) – g(a)]}}×g'(c) = 0[/Tex]

⇒ [Tex]\frac{f'(c) }{g'(c)} = \frac{[f(b) – f(a)] }{ [g(b) – g(a)]}[/Tex]

Thus, Cauchy’s Theorem is proved.

Limitations of Cauchy’s Mean Value Theorem

There are few limitations of the Cauchy’s Mean Value Theorem that are,

• Cauchy’s Mean Value Theorem is applicable only for continuous function.
• Cauchy’s Mean Value Theorem is applicable only for differentiable function.

Applications of Cauchy’s Mean Value Theorem

Various applications of Cauchy’s Mean Value theorem are,

• It is used to solve various problem in Real Analysis.
• It is used to predict the behaviours of various curves.
• It is used to derive Lagrange’s and Rolle’s Mean value theorems, etc.

Read More:

• Rolle’s Theorem and Lagrange’s Mean Value Theorem
• Continuity and Discontinuity
• Critical Points

Solved Examples on Cauchy’s Mean Value Theorem

Example 1: Find ‘c’ of Cauchy’s Mean Value Theorem for the functions f(x) = 3x² + 4x + 5 and g(x) = x² – x + 25 in the interval [1, 2]

Solution:

Given,

• f(x) = 3x² + 4x + 5
• g(x) = x² – x + 25

f(x) and g(x) are polynomial functions and thus,

• f(x), g(x) are continuous in the closed interval [Tex]a \leqslant x \leqslant b, x \in [1, 2][/Tex]
• f(x), g(x) are differentiable in the open interval a < x < b, i.e. x ϵ (1, 2)

And g'(x) = 2x – 1, is not equal to zero(0) in the interval [Tex]x \in [1, 2][/Tex]

Thus, Cauchy’s Mean value theorem is applicable on f(x) and g(x)

• f(x) = 3x² + 4x + 5
• g(x) = x² – x + 25

Differentiating f(x) and g(x) with respect to x

• f'(x) = 6x + 4
• g'(x) = 2x – 1

Now,

f(a) = f(1) = 12,

f(b) = f(2) = 25,

g(a) = g(1) = 25,

g(b) = g(2) = 27,

f'(c) = 6c + 4, and g'(c) = 2c – 1

Using Cauchy Mean Value Theorem,

[Tex]\frac{f'(c)}{ g'(c)} = \frac{[f(b) – f(a)]}{[g(b) – g(a)]}[/Tex]

⇒ [Tex]\frac{(6c + 4)}{(2c – 1)} = \frac{(25 – 12)}{(27 -25)}[/Tex]

⇒ [Tex]\frac{(6c + 4)}{(2c – 1)} = \frac{13}{2}[/Tex]

⇒ [Tex](6c + 4).2 = 13.(2c – 1)[/Tex]

⇒ [Tex]12c + 8 = 26c – 13[/Tex]

⇒ [Tex]26c – 12c = 13 + 8[/Tex]

⇒ [Tex]14c = 21[/Tex]

⇒ [Tex]c = \frac{21}{14} = \frac{3}{2} = 1.5 \in[1, 2][/Tex]

Example 2: Find ‘c’ of Cauchy’s Mean Value Theorem for the functions f(x) = 2.ln x and g(x) = x² – 1 in the interval [2, 3]

Solution:

Given,

• f(x) = 2.ln x
• g(x) = x²

f(x) is a polynomial functions and g(x) is a polynomial function both are continuous and differentiable on the given interval

• f(x), g(x) are continuous in the closed interval [Tex]a \leqslant x \leqslant b, x \in[2, 3][/Tex]
• f(x), g(x) are differentiable in the open interval a < x < b, i.e. [Tex]x \in (2, 3)[/Tex]

And g'(x) = 2x, is not equal to zero(0) in the interval x ϵ [1, 2]

Thus, Cauchy’s Mean value theorem is applicable on f(x) and g(x)

• f(x) = 2.ln x
• g(x) = x²

Differentiating f(x) and g(x) with respect to x

• f'(x) = 2/x
• g'(x) = 2x

Now,

f(a) = f(2) = 2. ln 2

f(b) = f(3) = 2. ln 3

g(a) = g(2) = 4

g(b) = g(3) = 9

f'(c) = 2/c

g'(c) = 2c

Using Cauchy Mean Value Theorem,

[Tex]\frac{f'(c) }{ g'(c)}= \frac{[f(b) – f(a)]} {[g(b) – g(a)]}[/Tex]

⇒ [Tex]\frac{(\frac{2}{c})}{(2c)}= \frac{(2. ln 3 – 2. ln 2)}{(9 – 4)}[/Tex]

⇒ 1/c² = 2(ln 3 – ln 2)/5

⇒ 1/c² = 2(ln 3/2)/5

⇒ [Tex]\frac{5}{2}[\frac{1}{ln(\frac{3}{2})}] = c^2[/Tex]

⇒ [Tex]c = \sqrt{\frac{(5/2)}{ln(3/2)}}[/Tex]

⇒ [Tex]c = 2.9 \in [2, 3][/Tex]

Practice Problems on Cauchy’s Mean Value Theorem

1. Let f(x)=x²+3x and g(x)=x+1. Find the point ccc in the interval [1,4] that satisfies Cauchy’s Mean Value Theorem.

2. Given f(x)=sin⁡(x) and g(x)=cos⁡(x), find c in the interval [Tex][0,\frac{π}{2}][/Tex] where Cauchy’s Mean Value Theorem applies.

3. For f(x)=e^x and g(x)=x, determine the point c in the interval [1,3] where Cauchy’s Mean Value Theorem holds.

4. For f(x)=x³ and g(x)=x, find c in the interval [0,2] where Cauchy’s Mean Value Theorem applies.

5. Given [Tex]f(x)=tan⁡(x)[/Tex] and g(x)=x, determine the point c in the interval [0,π/4] where Cauchy’s Mean Value Theorem is satisfied.

Summary

The Cauchy Mean Value Theorem extends the classic Mean Value Theorem by considering two functions rather than one, providing a more nuanced insight into the relationship between them. Specifically, it states that if two functions f(x) and g(x) are continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists at least one point ccc in (a,b) where the ratio of their derivatives equals the ratio of their function values.

This theorem is particularly useful in analyzing the comparative rates of change of two functions, and it often helps in proving important results in calculus and analysis. It generalizes the Mean Value Theorem by not only considering the rate of change of a single function but also how two functions change relative to each other, thereby deepening our understanding of their interdependencies and behaviors over an interval.

FAQs on Cauchy’s Mean Value Theorem

What is Cauchy’s Mean Value Theorem?

Cauchy’s Mean Value Theorem is the fundamental theorem of mathematics which states that, for any function f(x) and g(x) if it is continuous on [a, b] and differntiable from (a, b) then,

[Tex]\frac{[f(b) – f(a)]}{[g(b) – g(a)]} =\frac{ f'(c) }{ g'(c)}[/Tex]

where c belongs to (a, b)

Who Proved Cauchy’s Mean Value Theorem?

Cauchy’s Mean Value Theorem is proved by Augustin Louis Cauchy and hence the name Cauchy’s Mean Value Theorem.

What are Applications of Cauchy’s Mean Value Theorem?

Applications of Cauchy’s Mean Value theorem are,

• It is used to solve various problem in Real Analysis.
• It is used to predict the behaviors of various curves.
• It is used to derive Lagrange’s and Rooles Mean value theorems, etc.

State Lagrange’s Mean Value Theorem.

Lagrange’s Mean Value Theorem state that,

For any function f(x) defined on [a, b],

• If it is continuous on ​[a, b]
• If it is differentiable on (a, b)

Then, there exists a real number c ϵ (a, b) such that,

[Tex]f'(c) = \frac{{f(b) – f(a)}}{(b – a)}[/Tex]

What is the other name of Cauchy Mean Value Theorem?

Cauchy Mean Value Theorem is also known as Second Mean Value Theorem or Extended Mean Value Theorem

Who proved the Cauchy Mean Value Theorem?

The Cauchy Mean Value Theorem was proved by the French Mathematician Augustin Louis Cauchy in 1823.

jaideeppyne1997

Follow

Improve

Article Tags :

• Engineering Mathematics
• GATE CS
• Mathematics
• School Learning
• Calculus

+1 More