Class 9 RD Sharma Solutions – Chapter 13 Linear Equation in Two Variable – Exercise 13.3 | Set 2

Last Updated : 30 Apr, 2021

Question 11: Draw the graph of the equation 2x + 3y = 12. From the graph, find the coordinates of the point:

(i) whose y-coordinates is 3.

(ii) whose x-coordinate is −3.

Solution:

Given:

2x + 3y = 12

We get,

$y=\frac{12-2x}{3}$

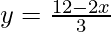
Substituting x = 0 in y = 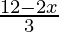$\frac{12-2x}{3}$ we get,

$y=\frac{12-2\times0}{3}$

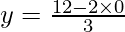
y = 4

Substituting x = 6 in 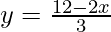$y= \frac{12-2x}{3}$ , we get

$y=\frac{12-2\times6}{3}$

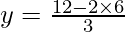
y = 4

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 6
y 4 0

By plotting the given equation on the graph, we get the point B (0, 4) and C (6,0).

(i) Co-ordinates of the point whose y axis is 3 are A 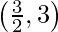$\left(\frac{3}{2},3\right)$

(ii) Co-ordinates of the point whose x -coordinate is –3 are D (-3, 6)

Question 12: Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:

(i) 6x − 3y = 12

(ii) −x + 4y = 8

(iii) 2x + y = 6

(iv) 3x + 2y + 6 = 0

Solution:

(i) Given:

6x – 3y = 12

We get,

$y=\frac{6x-12}{3}$

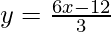
Now, substituting x = 0 in 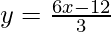$y=\frac{6x-12}{3}$ , we get

y = -4

Substituting x = 2 in 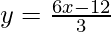$y=\frac{6x-12}{3}$ , we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 2
y -4 0

Co-ordinates of the points where graph cuts the co-ordinate axes are at y = -4 axis and x = 2

at x axis.

(ii) Given:

-x + 4y = 8

We get,

$y=\frac{8+x}{4}$

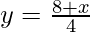
Now, substituting x = 0 in 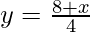$y=\frac{8+x}{4}$ , we get

y = 2

Substituting x = -8 in 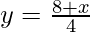$y=\frac{8+x}{4}$ , we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 -8
y 2 0

Co-ordinates of the points where graph cuts the co-ordinate axes are at y = 2 axis and x = -8

at x axis.

(iii) Given:

2x + y = 6

We get,

y = 6 – 2x

Now, substituting x= 0 in y = 6 – 2x w e get

y = 6

Substituting x = 3 in y = 6 – 2x, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 3
y 6 0

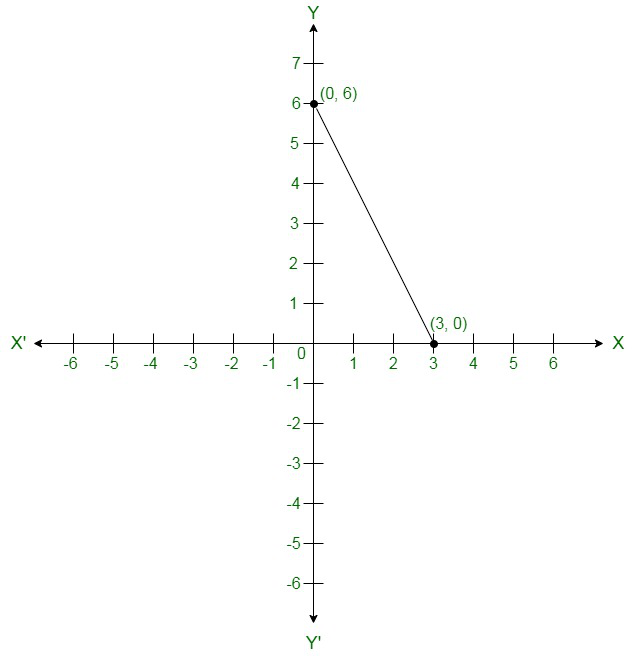
Co-ordinates of the points where graph cuts the co-ordinate axes are y = 6 at y axis and x = 3

at x axis.

(iv) Given:

3x + 2y + 6 = 0

We get,

$y = \frac{-(6+3x)}{2}$

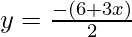
Now, substituting x = -2 in 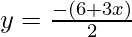$y = \frac{-(6+3x)}{2}$ , we get

y = -3

Substituting x = -2 in 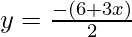$y = \frac{-(6+3x)}{2}$ , we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 -2
y -3 0

Co-ordinates of the points where graph cuts the co-ordinate axes are y = -3 at y axis and x = -2

at x axis.

Question 13: Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region.

Solution:

Given:

2x + y = 6

We get,

y = 6 – 2 x

Now, substituting x = 0 in y = 6 – 2x ,we get

y = 6

Substituting x = 3 in y = 6 – 2x ,we get

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 3
y 6 0

The region bounded by the graph is ABC which forms a triangle.

AC at y axis is the base of triangle having AC = 6 units on y axis.

BC at x axis is the height of triangle having BC = 3 units on x axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(6\times3)$

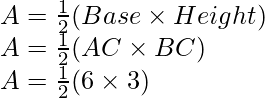
A = 9 sq. units

Question 14: Draw the graph of the equation $\frac{x}{3}+\frac{y}{4}=1$ . Also, find the area of the triangle formed by the line and the coordinates axes.

Solution:

Given:

$\frac{x}{3}+\frac{y}{4}=1$

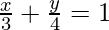
4x + 3y = 12

We get,

$y=\frac{12-4x}{3}$

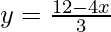
Now, substituting x = 0 in 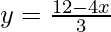$y=\frac{12-4x}{3}$ , we get

y = 4

Substituting x = 3 in 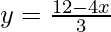$y=\frac{12-4x}{3}$ , we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 3
y 4 0

The region bounded by the graph is ABC which form a triangle.

AC at y axis is the base of triangle having AC = 4 units on y axis.

BC at x axis is the height of triangle having BC = 3 units on x axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(4\times3)$

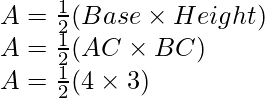
A = 6 sq. units

Question 15: Draw the graph of y = | x |.

Solution:

We are given,

y = |x|

Substituting, x = 1 we get

y = 1

Substituting, x = -1 we get

y = 1

Substituting,x = 2 we get

y = 2

Substituting, x = -2 we get

y = 2

For every value of x, whether positive or negative, we get y as a positive number.

Question 16: Draw the graph of y = | x | + 2.

Solution:

Given:

y = |x| + 2

Substituting, x = 0 we get

y = 2

Substituting, x = 1 we get

y = 3

Substituting, x = -1 we get

y = 3

Substituting, x = 2 we get

y = 4

Substituting, x = -2 we get

y = 4

For every value of x, whether positive or negative, we get y as a positive number and the minimum value of y is equal to 2 units.

Question 17: Draw the graphs of the following linear equations on the same graph paper:

2x + 3y = 12, x − y = 1

Find the coordinates of the vertices of the triangle formed by the two straight lines and the area bounded by these lines and x-axis.

Solution:

Given:

2x + 3y = 12

We get,

$y=\frac{12-2x}{3}$

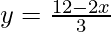
Now, substituting x = 0 in 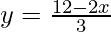$y=\frac{12-2x}{3}$ , we get

y = 4

Substituting x = 6 in 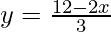$y=\frac{12-2x}{3}$ , we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 6
y 4 0

Plotting A(0,4) and E(6,0) on the graph and by joining the points , we obtain the graph of equation .

Given:

x – y = 1

We get,

y = x − 1

Now, substituting x = 0 in y = x − 1,we get

y = −1

Substituting x = -1 in y = x − 1,we get

y = −2

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 -1
y -1 -2

Plotting D(0,1) and E(-1,0) on the graph and by joining the points , we obtain the graph of equation .

By the intersection of lines formed by 2x + 3y = 12 and x – y = 1 on the graph, triangle ABC is formed on y axis.

Therefore,

AC at y axis is the base of triangle ABC having AC = 5 units on y axis.

Draw FE perpendicular from F on y axis.

FE parallel to x axis is the height of triangle ABC having FE = 3 units on x axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(5\times3)\\ =\frac{15}{2}sq.\ units$

Question 18: Draw the graphs of the linear equations 4x − 3y + 4 = 0 and 4x + 3y −20 = 0. Find the area bounded by these lines and x-axis.

Solution:

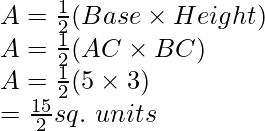
Given:

4x – 3y + 4 = 0

We get,

$y=\frac{4x+4}{3}$

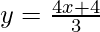
Now, substituting x = 0 in 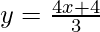$y=\frac{4x+4}{3}$ , we get

$y=\frac{4}{3}$

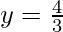
Substituting x = -1 in 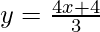$y=\frac{4x+4}{3}$ , we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 -1
y 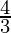$\frac{4}{3}$ 0

Plotting E(0, 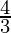$\frac{4}{3}$ ) and A(-1,0) on the graph and by joining the points, we obtain the graph of equation.

We are given,

4x + 3y – 20 = 0

We get,

$y=\frac{20-4x}{3}$

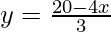
Now, substituting x = 0 in 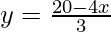$y=\frac{20-4x}{3}$ , we get

$y=\frac{20}{3}$

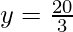
Substituting x = 5 in 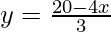$y=\frac{20-4x}{3}$ , we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 5
y 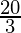$\frac{20}{3}$ 0

Plotting D(0, 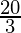$\frac{20}{3}$ ) and B(5,0) on the graph and by joining the points, we obtain the graph of equation.

By the intersection of lines formed by 4x – 3y + 4 = 0 and 4x + 3y – 20 = 0 on the graph, triangle ABC is formed on x axis.

Therefore,

AB at x axis is the base of triangle ABC having AB = 6 units on x axis.

Draw CF perpendicular from C on x axis.

CF parallel to y axis is the height of triangle ABC having CF = 4 units on y axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(6\times4)\\ A=12sq.\ units$

Question 19: The path of a train A is given by the equation 3x + 4y − 12 = 0 and the path of another train B is given by the equation 6x + 8y − 48 = 0. Represent this situation graphically.

Solution:

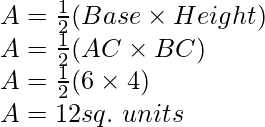
Given: Path of train A,

3x + 4y – 12 = 0

We get,

$y=\frac{12-3x}{4}$

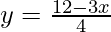
Now, substituting x = 0 in 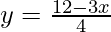$y=\frac{12-3x}{4}$ ,we get

y = 3

Substituting x = 4 in 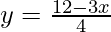$y=\frac{12-3x}{4}$ ,we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 4
y 3 0

Plotting A(4,0) and E(0,3) on the graph and by joining the points , we obtain the graph of equation .

We are given the path of train B,

6x + 8y – 48 = 0

We get,

$y=\frac{48-6x}{8}$

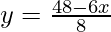
Now, substituting x = 0 in 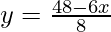$y=\frac{48-6x}{8}$ ,we get

y = 6

Substituting x = 8 in 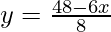$y=\frac{48-6x}{8}$ ,we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 8
y 6 0

Plotting C(0,6) and D(8,0) on the graph and by joining the points , we obtain the graph of equation.

Question 20: Ravish tells his daughter Aarushi, ”Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. If present ages of Aarushi and Ravish are x and y years respectively, represent this situation algebraically as well as graphically.

Solution:

We are given the present age of Ravish as y years and Aarushi as x years.

Age of Ravish seven years ago = y – 7

Age of Aarushi seven years ago = x – 7

It has already been said by Ravish that seven years ago he was seven times old then Aarushi was then

So,

y – 7 = 7(x – 7)

y – 7 = 7x – 49

7x – y = -7 + 49

7x – y – 42 = 0

Age of Ravish three years from now = y + 3

Age of Aarushi three years from now = x + 3

It has already been said by Ravish that three years from now he will be three times old then Aarushi will be then

So,

y + 3 = 3(x + 3)

y + 3 = 3x + 9

3x + 9 – y – 3 = 0

3x – y + 6 = 0

(1) and (2) are the algebraic representation of the given statement.

Given:

7x – y – 42 = 0

We get,

y = 7x – 42

Now, substituting x = 0 in y = 7x – 42 ,we get

y = -42

Substituting x = 6 in y = 7x – 42, we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 6
y -42 0

Given:

3x – y + 6 = 0

We get,

y = 3x + 6

Now, substituting x = 0 in y = 3x + 6 ,we get

y = 6

Substituting x = -2 in y = 3x + 6 ,we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x 0 -2
y 6 0

The red -line represents the equation. 7x – y – 42 = 0

The blue-line represents the equation. 3x – y + 6 = 0

Question 21: Aarushi was driving a car with uniform speed of 60km/h. Draw distance-time graph. From the graph, find the distance traveled by Aarushi in

(i) $2\frac{1}{2}$ Hours

(ii) $\frac{1}{2}$ Hour

Solution:

Aarushi is driving the car with the uniform speed of 60 km/h.

We represent time on X-axis and distance on Y-axis

Now, graphically

We are given that the car is travelling with a uniform speed 60 km/hr. This means car travels 60 km distance each hour. Thus the graph we get is of a straight line.

Also, we know when the car is at rest, the distance traveled is 0 km, speed is 0 km/hr and the time is also 0 hr.

Therefore, the given straight line will pass through O(0,0) and M(1,60).

Join the points O and M and extend the line in both directions.

Now, we draw a dotted line parallel to y-axis from x = 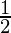$\frac{1}{2}$ that meets the straight line graph at L from which we draw a line parallel to x-axis that crosses y-axis at 30. Thus, in 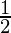$\frac{1}{2}$ hr, distance traveled by the car is 30 km.

Now, we draw a dotted line parallel to y-axis from x = 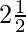$2\frac{1}{2}$ that meets the straight line graph at N from which we draw a line parallel to x-axis that crosses y-axis at 150. Thus, in 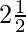$2\frac{1}{2}$ hr, distance traveled by the car is 150 km.

(i) Distance = Speed × Time

Distance traveled in 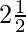$2\frac{1}{2}$ hours is given by

Distance = $60\times2\frac{1}{2}$

Distance = $60\times\frac{5}{2}$

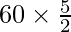
Distance = 150 km

(ii) Distance = Speed × Time

Distance traveled in 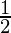$\frac{1}{2}$ hours is given by

Distance = 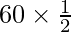$60\times\frac{1}{2}$

Distance = 30 km

Class 9 RD Sharma Solutions - Chapter 14 Quadrilaterals- Exercise 14.1

codersgram9

Improve

Article Tags :

Class 9 RD Sharma Solutions – Chapter 13 Linear Equation in Two Variable – Exercise 13.3 | Set 2

Question 11: Draw the graph of the equation 2x + 3y = 12. From the graph, find the coordinates of the point:

Question 12: Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:

Question 13: Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region.

Question 14: Draw the graph of the equation . Also, find the area of the triangle formed by the line and the coordinates axes.

Question 15: Draw the graph of y = | x |.

Question 16: Draw the graph of y = | x | + 2.

Question 17: Draw the graphs of the following linear equations on the same graph paper:

Find the coordinates of the vertices of the triangle formed by the two straight lines and the area bounded by these lines and x-axis.

Question 18: Draw the graphs of the linear equations 4x − 3y + 4 = 0 and 4x + 3y −20 = 0. Find the area bounded by these lines and x-axis.

Question 19: The path of a train A is given by the equation 3x + 4y − 12 = 0 and the path of another train B is given by the equation 6x + 8y − 48 = 0. Represent this situation graphically.

Question 21: Aarushi was driving a car with uniform speed of 60km/h. Draw distance-time graph. From the graph, find the distance traveled by Aarushi in

Similar Reads

Chapter 1: Number Systems

Chapter 2: Exponents and Powers of Real Numbers

Chapter 3: Rationalisation

Chapter 4: Algebraic Identities

Chapter 5: Factorization of Algebraic Expressions

Chapter 6: Factorization of Polynomials

Chapter 7: Introduction to Euclidâ€™s Geometry

Chapter 8: Lines and Angles

Chapter 9: Triangle and Its Angles

Chapter 10: Congruent Triangles

Chapter 11: Coordinate Geometry

Chapter 12: Heronâ€™s Formula

Chapter 13: Linear Equations in Two Variables

Chapter 14: Quadrilaterals

Chapter 15: Areas of Parallelograms and Triangles

Chapter 16: Circles

Chapter 17: Constructions

Chapter 18: Surface Area and Volume of a Cuboid and a Cube

Chapter 19: Surface Area and Volume of a Right Circular Cylinder

Chapter 20: Surface Area and Volume of a Right Circular Cone

Chapter 21: Surface Area and Volume of a Sphere

Chapter 22: Tabular Representation of Statistical Data

Chapter 23: Graphical Representation of Statistical Data

Chapter 24: Measures of Central Tendency

Chapter 25: Probability

What kind of Experience do you want to share?

Question 14: Draw the graph of the equation $\frac{x}{3}+\frac{y}{4}=1$ . Also, find the area of the triangle formed by the line and the coordinates axes.