Coin Change – Count Ways to Make Sum

Last Updated : 16 Nov, 2024

Try it on GfG Practice

Given an integer array of coins[] of size n representing different types of denominations and an integer sum, the task is to count all combinations of coins to make a given value sum.

Note: Assume that you have an infinite supply of each type of coin.

Examples:

Input: sum = 4, coins[] = [1, 2, 3]
Output: 4
Explanation: There are four solutions: [1, 1, 1, 1], [1, 1, 2], [2, 2] and [1, 3]

Input: sum = 10, coins[] = [2, 5, 3, 6]
Output: 5
Explanation: There are five solutions:
[2, 2, 2, 2, 2], [2, 2, 3, 3], [2, 2, 6], [2, 3, 5] and [5, 5]

Input: sum = 10, coins[] = [10]
Output: 1
Explanation: The only is to pick 1 coin of value 10.

Input: sum = 5, coins[] = [4]
Output: 0
Explanation: We cannot make sum 5 with the given coins

Table of Content

Using Recursion – O(2^sum) Time and O(sum) Space
Using Top-Down DP (Memoization) – O(sum*n) Time and O(sum*n) Space
Using Bottom-Up DP (Tabulation) – O(sum*n) Time and O(sum*n) Space
Using Space Optimized DP – O(sum*n) Time and O(sum) Space

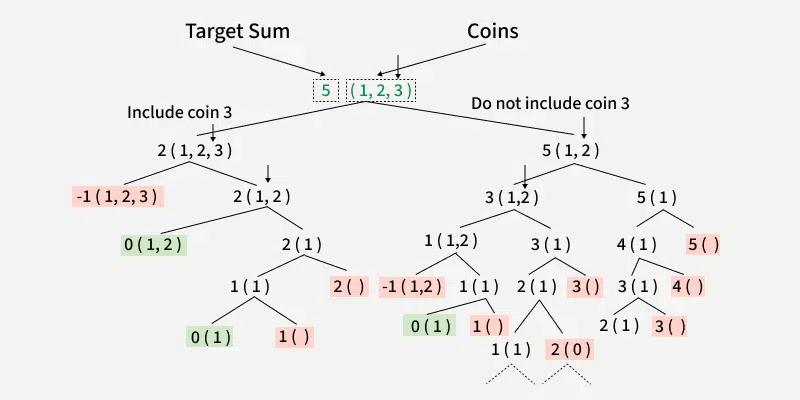
Using Recursion – O(2^sum) Time and O(sum) Space

For each coin, there are 2 options:

Include the current coin: Subtract the current coin’s denomination from the target sum and call the count function recursively with the updated sum and the same set of coins i.e., count(coins, n, sum – coins[n-1] )
Exclude the current coin: Call the count function recursively with the same sum and the remaining coins. i.e., count(coins, n-1,sum ).
Recurrence Relation: The final result will be the sum of both cases.

count(coins, n, sum) = count(coins, n, sum-count[n-1]) + count(coins, n-1, sum)

Base cases:

If the target sum (sum) is 0, there is only one way to make the sum, which is by not selecting any coin. So, count(0, coins, n) = 1.
If the target sum (sum) is negative or no coins are left to consider (n == coins.size), then there are no ways to make the sum, so count(sum, coins, 0) = 0.

coin---------change_________

C++

// C++ program for coin change problem
// using recursion
#include <bits/stdc++.h>
using namespace std;

// Returns the count of ways we can
// sum coins[0...n-1] coins to get sum "sum"
int countRecur(vector<int>& coins, int n, int sum) {
  
    // If sum is 0 then there is 1 solution
    // (do not include any coin)
    if (sum == 0) return 1;

    // 0 ways in the following two cases
    if (sum < 0 || n == 0) return 0;

    // count is sum of solutions (i)
    // including coins[n-1] (ii) excluding coins[n-1]
    return countRecur(coins, n, sum - coins[n - 1]) + 
            countRecur(coins, n - 1, sum);
}

int count(vector<int> &coins, int sum) {
    return countRecur(coins, coins.size(), sum);
}

int main() {
    vector<int> coins = {1, 2, 3};
    int sum = 5;
    cout << count(coins, sum);
    return 0;
}

Java

// Java program for coin change problem.
// using recursion

class GfG {

    static int countRecur(int[] coins, int n, int sum) {

        // If sum is 0 then there is 1 solution
        // (do not include any coin)
        if (sum == 0) return 1;

        // 0 ways in the following two cases
        if (sum < 0 || n == 0) return 0;

        // count is sum of solutions (i)
        // including coins[n-1] (ii) excluding coins[n-1]
        return countRecur(coins, n, sum - coins[n - 1]) +
                countRecur(coins, n - 1, sum);
    }

    static int count(int[] coins, int sum) {
        return countRecur(coins, coins.length, sum);
    }

    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int sum = 5;
        System.out.println(count(coins, sum));
    }
}

Python

# Python program for coin change problem.
# using recursion

def countRecur(coins, n, sum):
  
    # If sum is 0 then there is 1 solution
    # (do not include any coin)
    if sum == 0:
        return 1

    # 0 ways in the following two cases
    if sum < 0 or n == 0:
        return 0

    # count is sum of solutions (i)
    # including coins[n-1] (ii) excluding coins[n-1]
    return countRecur(coins, n, sum - coins[n - 1]) + \
              countRecur(coins, n - 1, sum)

def count(coins, sum):
    return countRecur(coins, len(coins), sum)

if __name__ == "__main__":
    coins = [1, 2, 3]
    sum = 5
    print(count(coins, sum))

C#

// C# program for coin change problem.
// using recursion

using System;

class GfG {

    static int countRecur(int[] coins, int n, int sum) {

        // If sum is 0 then there is 1 solution
        // (do not include any coin)
        if (sum == 0) return 1;

        // 0 ways in the following two cases
        if (sum < 0 || n == 0) return 0;

        // count is sum of solutions (i)
        // including coins[n-1] (ii) excluding coins[n-1]
        return countRecur(coins, n, sum - coins[n - 1]) +
               countRecur(coins, n - 1, sum);
    }

    static int count(int[] coins, int sum) {
        return countRecur(coins, coins.Length, sum);
    }

    static void Main() {
        int[] coins = {1, 2, 3};
        int sum = 5;
        Console.WriteLine(count(coins, sum));
    }
}

JavaScript

// JavaScript program for coin change problem.
// using recursion

function countRecur(coins, n, sum) {

    // If sum is 0 then there is 1 solution
    // (do not include any coin)
    if (sum === 0) return 1;

    // 0 ways in the following two cases
    if (sum < 0 || n === 0) return 0;

    // count is sum of solutions (i)
    // including coins[n-1] (ii) excluding coins[n-1]
    return countRecur(coins, n, sum - coins[n - 1]) +
           countRecur(coins, n - 1, sum);
}

function count(coins, sum) {
    return countRecur(coins, coins.length, sum);
}

const coins = [1, 2, 3];
const sum = 5;
console.log(count(coins, sum));

Output

Using Top-Down DP (Memoization) – O(sumn) Time and O(sumn) Space

1. Optimal Substructure: Number of ways to make sum at index i, i.e., count(i, sum, coins), depends on the optimal solutions of the subproblems count(i, sum-coins[i], coins) , and count(i+1, sum, coins). By adding these optimal substructures, we can efficiently calculate the number of ways to make target sum at index i.

2. Overlapping Subproblems: While applying a recursive approach in this problem, we notice that certain subproblems are computed multiple times.

Follow the below steps to Implement the idea:

Since there are two parameters that change during recursive calls, we create a 2D memo array to store the results of previously solved subproblems.
Since the range of recursion parameters goes from 0 to n and 0 to sum, we keep dimensions of the 2D array as (n+1) x (sum + 1)
memo[i][j] will represent the number of distinct ways to make the sum j by using the first i coins.
During the recursion call, if the same state is called more than once, then we can directly return the answer stored for that state instead of calculating again.

C++

// C++ program for coin change problem
// using memoization
#include <bits/stdc++.h>
using namespace std;

// Returns the count of ways we can
// sum coins[0...n-1] coins to get sum "sum"
int countRecur(vector<int>& coins, int n, int sum, 
               vector<vector<int>> &memo) {
  
    // If sum is 0 then there is 1 solution
    // (do not include any coin)
    if (sum == 0) return 1;

    // 0 ways in the following two cases
    if (sum < 0 || n == 0) return 0;
    
    // If the subproblem is previously calculated then
    // simply return the result
    if (memo[n-1][sum]!=-1) return memo[n-1][sum];

    // count is sum of solutions (i)
    // including coins[n-1] (ii) excluding coins[n-1]
    return memo[n-1][sum] = 
        countRecur(coins, n, sum - coins[n-1], memo) + 
        countRecur(coins, n - 1, sum, memo);
}

int count(vector<int> &coins, int sum) {
    
    vector<vector<int>> memo(coins.size(), vector<int>(sum+1, -1));
    return countRecur(coins, coins.size(), sum, memo);
}

int main() {
    vector<int> coins = {1, 2, 3};
    int sum = 5;
    cout << count(coins, sum);
    return 0;
}

Java

// Java program for coin change problem.
// using memoization
import java.util.Arrays;

class GfG {

    static int countRecur(int[] coins, int n, int sum, int[][] memo) {

        // If sum is 0 then there is 1 solution
        // (do not include any coin)
        if (sum == 0) return 1;

        // 0 ways in the following two cases
        if (sum < 0 || n == 0) return 0;

        // If the subproblem is previously calculated then
        // simply return the result
        if (memo[n - 1][sum] != -1) return memo[n - 1][sum];

        // count is sum of solutions (i)
        // including coins[n-1] (ii) excluding coins[n-1]
        return memo[n - 1][sum] = 
                countRecur(coins, n, sum - coins[n - 1], memo) + 
                countRecur(coins, n - 1, sum, memo);
    }

    static int count(int[] coins, int sum) {
        int[][] memo = new int[coins.length][sum + 1];
        for (int[] row : memo) {
            Arrays.fill(row, -1);
        }
        return countRecur(coins, coins.length, sum, memo);
    }

    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int sum = 5;
        System.out.println(count(coins, sum));
    }
}

Python

# Python program for coin change problem.
# using memoization
def countRecur(coins, n, sum, memo):
  
    # If sum is 0 then there is 1 solution
    # (do not include any coin)
    if sum == 0:
        return 1

    # 0 ways in the following two cases
    if sum < 0 or n == 0:
        return 0

    # If the subproblem is previously calculated then
    # simply return the result
    if memo[n - 1][sum] != -1:
        return memo[n - 1][sum]

    # count is sum of solutions (i)
    # including coins[n-1] (ii) excluding coins[n-1]
    memo[n - 1][sum] = (countRecur(coins, n, sum - coins[n - 1], memo) + 
                        countRecur(coins, n - 1, sum, memo))
    return memo[n - 1][sum]

def count(coins, sum):
    memo = [[-1 for _ in range(sum + 1)] for _ in range(len(coins))]
    return countRecur(coins, len(coins), sum, memo)

if __name__ == "__main__":
    coins = [1, 2, 3]
    sum = 5
    print(count(coins, sum))

C#

// C# program for coin change problem.
// using memoization

using System;

class GfG {

    static int countRecur(int[] coins, int n, int sum, int[,] memo) {

        // If sum is 0 then there is 1 solution
        // (do not include any coin)
        if (sum == 0) return 1;

        // 0 ways in the following two cases
        if (sum < 0 || n == 0) return 0;

        // If the subproblem is previously calculated then
        // simply return the result
        if (memo[n - 1, sum] != -1) return memo[n - 1, sum];

        // count is sum of solutions (i)
        // including coins[n-1] (ii) excluding coins[n-1]
        memo[n - 1, sum] = 
            countRecur(coins, n, sum - coins[n - 1], memo) + 
            countRecur(coins, n - 1, sum, memo);
        return memo[n - 1, sum];
    }

    static int count(int[] coins, int sum) {
        int[,] memo = new int[coins.Length, sum + 1];
        for (int i = 0; i < coins.Length; i++) {
            for (int j = 0; j <= sum; j++) {
                memo[i, j] = -1;
            }
        }
        return countRecur(coins, coins.Length, sum, memo);
    }

    static void Main() {
        int[] coins = {1, 2, 3};
        int sum = 5;
        Console.WriteLine(count(coins, sum));
    }
}

JavaScript

// JavaScript program for coin change problem.
// using memoization

function countRecur(coins, n, sum, memo) {

    // If sum is 0 then there is 1 solution
    // (do not include any coin)
    if (sum === 0) return 1;

    // 0 ways in the following two cases
    if (sum < 0 || n === 0) return 0;

    // If the subproblem is previously calculated then
    // simply return the result
    if (memo[n - 1][sum] !== -1) return memo[n - 1][sum];

    // count is sum of solutions (i)
    // including coins[n-1] (ii) excluding coins[n-1]
    memo[n - 1][sum] = countRecur(coins, n, sum - coins[n - 1], memo) + 
                       countRecur(coins, n - 1, sum, memo);
    return memo[n - 1][sum];
}

function count(coins, sum) {
    const memo = Array.from({ length: coins.length }, () => Array(sum + 1).fill(-1));
    return countRecur(coins, coins.length, sum, memo);
}

const coins = [1, 2, 3];
const sum = 5;
console.log(count(coins, sum));

Output

Using Bottom-Up DP (Tabulation) – O(sumn) Time and O(sumn) Space

The idea is to fill the DP table based on previous values. For each coin, we either include it or exclude it to compute the minimum number of coins needed for each sum. The table is filled in an iterative manner from i = n-1 to i = 0 and for each sum from 1 to sum.

The dynamic programming relation is as follows:

if (sum-coins[i]) is greater than 0, then dp[i][sum] = dp[i][sum-coins[i]] + dp[i+1][sum].
else dp[i][sum] = dp[i+1][sum].

C++

// C++ program for coin change problem using tabulation
#include <bits/stdc++.h>
using namespace std;

// Returns total distinct ways to make sum using n coins of
// different denominations
int count(vector<int>& coins, int sum) {
    int n = coins.size();
    
    // 2d dp array where n is the number of coin
    // denominations and sum is the target sum
    vector<vector<int> > dp(n + 1, vector<int>(sum + 1, 0));

    // Represents the base case where the target sum is 0,
    // and there is only one way to make change: by not
    // selecting any coin
    dp[0][0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= sum; j++) {

            // Add the number of ways to make change without
            // using the current coin,
            dp[i][j] += dp[i - 1][j];

            if ((j - coins[i - 1]) >= 0) {

                // Add the number of ways to make change
                // using the current coin
                dp[i][j] += dp[i][j - coins[i - 1]];
            }
        }
    }
    return dp[n][sum];
}

int main() {
    vector<int> coins = {1, 2, 3};
    int sum = 5;
    cout << count(coins, sum);
    return 0;
}

Java

// Java program for coin change problem using tabulation

class GfG {

    static int count(int[] coins, int sum) {
        int n = coins.length;
        
        // 2d dp array where n is the number of coin
        // denominations and sum is the target sum
        int[][] dp = new int[n + 1][sum + 1];

        // Represents the base case where the target sum is 0,
        // and there is only one way to make change: by not
        // selecting any coin
        dp[0][0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= sum; j++) {

                // Add the number of ways to make change without
                // using the current coin
                dp[i][j] += dp[i - 1][j];

                if ((j - coins[i - 1]) >= 0) {

                    // Add the number of ways to make change
                    // using the current coin
                    dp[i][j] += dp[i][j - coins[i - 1]];
                }
            }
        }
        return dp[n][sum];
    }

    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int sum = 5;
        System.out.println(count(coins, sum));
    }
}

Python

# Python program for coin change problem using tabulation

def count(coins, sum):
    n = len(coins)
    
    # 2d dp array where n is the number of coin
    # denominations and sum is the target sum
    dp = [[0] * (sum + 1) for _ in range(n + 1)]

    # Represents the base case where the target sum is 0,
    # and there is only one way to make change: by not
    # selecting any coin
    dp[0][0] = 1
    for i in range(1, n + 1):
        for j in range(sum + 1):

            # Add the number of ways to make change without
            # using the current coin
            dp[i][j] += dp[i - 1][j]

            if (j - coins[i - 1]) >= 0:

                # Add the number of ways to make change
                # using the current coin
                dp[i][j] += dp[i][j - coins[i - 1]]
                
    return dp[n][sum]

if __name__ == "__main__":
    coins = [1, 2, 3]
    sum = 5
    print(count(coins, sum))

C#

// C# program for coin change problem using tabulation

using System;

class GfG {

    static int count(int[] coins, int sum) {
        int n = coins.Length;
        
        // 2d dp array where n is the number of coin
        // denominations and sum is the target sum
        int[,] dp = new int[n + 1, sum + 1];

        // Represents the base case where the target sum is 0,
        // and there is only one way to make change: by not
        // selecting any coin
        dp[0, 0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= sum; j++) {

                // Add the number of ways to make change without
                // using the current coin
                dp[i, j] += dp[i - 1, j];

                if ((j - coins[i - 1]) >= 0) {

                    // Add the number of ways to make change
                    // using the current coin
                    dp[i, j] += dp[i, j - coins[i - 1]];
                }
            }
        }
        return dp[n, sum];
    }

    static void Main() {
        int[] coins = {1, 2, 3};
        int sum = 5;
        Console.WriteLine(count(coins, sum));
    }
}

JavaScript

// JavaScript program for coin change problem using tabulation

function count(coins, sum) {
    const n = coins.length;
    
    // 2d dp array where n is the number of coin
    // denominations and sum is the target sum
    const dp = Array.from({ length: n + 1 }, () => Array(sum + 1).fill(0));

    // Represents the base case where the target sum is 0,
    // and there is only one way to make change: by not
    // selecting any coin
    dp[0][0] = 1;
    for (let i = 1; i <= n; i++) {
        for (let j = 0; j <= sum; j++) {

            // Add the number of ways to make change without
            // using the current coin
            dp[i][j] += dp[i - 1][j];

            if ((j - coins[i - 1]) >= 0) {

                // Add the number of ways to make change
                // using the current coin
                dp[i][j] += dp[i][j - coins[i - 1]];
            }
        }
    }
    return dp[n][sum];
}

const coins = [1, 2, 3];
const sum = 5;
console.log(count(coins, sum));

Output

Using Space Optimized DP – O(sum*n) Time and O(sum) Space

In previous approach of dynamic programming we have derive the relation between states as given below:

if (sum-coins[i]) is greater than 0, then dp[i][sum] = dp[i][sum-coins[i]] + dp[i+1][sum].
else dp[i][sum] = dp[i+1][sum].
If we observe that for calculating current dp[i][sum] state we only need previous row dp[i-1][sum] or current row dp[i][sum-coins[i]]. There is no need to store all the previous states just one previous state is used to compute result.

C++

// C++ program for coin change problem
// using space optimised dp
#include <bits/stdc++.h>
using namespace std;

// Returns total distinct ways to make sum using n coins of
// different denominations
int count(vector<int> &coins, int sum) {
    int n = coins.size();
    
    // dp[i] will be storing the number of solutions for
    // value i. We need sum+1 rows as the dp is
    // constructed in bottom up manner using the base case
    // (sum = 0)
    vector<int> dp(sum + 1);

    // Base case (If given value is 0)
    dp[0] = 1;

    // Pick all coins one by one and update the table[]
    // values after the index greater than or equal to the
    // value of the picked coin
    for (int i = 0; i < n; i++)
        for (int j = coins[i]; j <= sum; j++)
            dp[j] += dp[j - coins[i]];
    return dp[sum];
}

int main() {
    vector<int> coins = {1, 2, 3};
    int sum = 5;
    cout << count(coins, sum);
    return 0;
}

Java

// Java program for coin change problem.
// using space optimised dp

class GfG {

    static int count(int[] coins, int sum) {
        int n = coins.length;
        
        // dp[i] will be storing the number of solutions for
        // value i. We need sum+1 rows as the dp is
        // constructed in bottom up manner using the base case
        // (sum = 0)
        int[] dp = new int[sum + 1];

        // Base case (If given value is 0)
        dp[0] = 1;

        // Pick all coins one by one and update the table[]
        // values after the index greater than or equal to the
        // value of the picked coin
        for (int i = 0; i < n; i++)
            for (int j = coins[i]; j <= sum; j++)
                dp[j] += dp[j - coins[i]];
                
        return dp[sum];
    }

    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int sum = 5;
        System.out.println(count(coins, sum));
    }
}

Python

# Python program for coin change problem.
# using space optimised dp

def count(coins, sum):
    n = len(coins)
    
    # dp[i] will be storing the number of solutions for
    # value i. We need sum+1 rows as the dp is
    # constructed in bottom up manner using the base case
    # (sum = 0)
    dp = [0] * (sum + 1)

    # Base case (If given value is 0)
    dp[0] = 1

    # Pick all coins one by one and update the table[]
    # values after the index greater than or equal to the
    # value of the picked coin
    for i in range(n):
        for j in range(coins[i], sum + 1):
            dp[j] += dp[j - coins[i]]
            
    return dp[sum]

if __name__ == "__main__":
    coins = [1, 2, 3]
    sum = 5
    print(count(coins, sum))

C#

// C# program for coin change problem.
// using space optimised dp

using System;

class GfG {

    static int count(int[] coins, int sum) {
        int n = coins.Length;
        
        // dp[i] will be storing the number of solutions for
        // value i. We need sum+1 rows as the dp is
        // constructed in bottom up manner using the base case
        // (sum = 0)
        int[] dp = new int[sum + 1];

        // Base case (If given value is 0)
        dp[0] = 1;

        // Pick all coins one by one and update the table[]
        // values after the index greater than or equal to the
        // value of the picked coin
        for (int i = 0; i < n; i++)
            for (int j = coins[i]; j <= sum; j++)
                dp[j] += dp[j - coins[i]];
                
        return dp[sum];
    }

    static void Main() {
        int[] coins = {1, 2, 3};
        int sum = 5;
        Console.WriteLine(count(coins, sum));
    }
}

JavaScript

// JavaScript program for coin change problem
// using space optimised dp

function count(coins, sum) {
    const n = coins.length;
    
    // dp[i] will be storing the number of solutions for
    // value i. We need sum+1 rows as the dp is
    // constructed in bottom up manner using the base case
    // (sum = 0)
    const dp = Array(sum + 1).fill(0);

    // Base case (If given value is 0)
    dp[0] = 1;

    // Pick all coins one by one and update the table[]
    // values after the index greater than or equal to the
    // value of the picked coin
    for (let i = 0; i < n; i++)
        for (let j = coins[i]; j <= sum; j++)
            dp[j] += dp[j - coins[i]];
            
    return dp[sum];
}

const coins = [1, 2, 3];
const sum = 5;
console.log(count(coins, sum));

Output

Related articles:

GeeksforGeeks

News

Improve

Similar Reads

Introduction to Knapsack Problem, its Types and How to solve them

The Knapsack problem is an example of the combinational optimization problem. This problem is also commonly known as the "Rucksack Problem". The name of the problem is defined from the maximization problem as mentioned below: Given a bag with maximum weight capacity of W and a set of items, each hav

Unbounded Fractional Knapsack

Given the weights and values of n items, the task is to put these items in a knapsack of capacity W to get the maximum total value in the knapsack, we can repeatedly put the same item and we can also put a fraction of an item. Examples: Input: val[] = {14, 27, 44, 19}, wt[] = {6, 7, 9, 8}, W = 50 Ou

Unbounded Knapsack (Repetition of items allowed)

Given a knapsack weight, say capacity and a set of n items with certain value vali and weight wti, The task is to fill the knapsack in such a way that we can get the maximum profit. This is different from the classical Knapsack problem, here we are allowed to use an unlimited number of instances of

Unbounded Knapsack (Repetition of items allowed) | Efficient Approach

Given an integer W, arrays val[] and wt[], where val[i] and wt[i] are the values and weights of the ith item, the task is to calculate the maximum value that can be obtained using weights not exceeding W. Note: Each weight can be included multiple times. Examples: Input: W = 4, val[] = {6, 18}, wt[]

Double Knapsack | Dynamic Programming

Given an array arr[] containing the weight of 'n' distinct items, and two knapsacks that can withstand capactiy1 and capacity2 weights, the task is to find the sum of the largest subset of the array 'arr', that can be fit in the two knapsacks. It's not allowed to break any items in two, i.e. an item

Article Tags :

Practice Tags :

翻译：