Given a weighted graph with V vertices and E edges, and a source vertex src, find the shortest path from the source vertex to all vertices in the given graph. If a vertex cannot be reached from source vertex, mark its distance as 108.
Note: If a graph contains negative weight cycle, return -1.
Examples:
Input: V = 5, edges = [[1, 3, 2], [4, 3, -1], [2, 4, 1], [1, 2, 1], [0, 1, 5]], src = 0
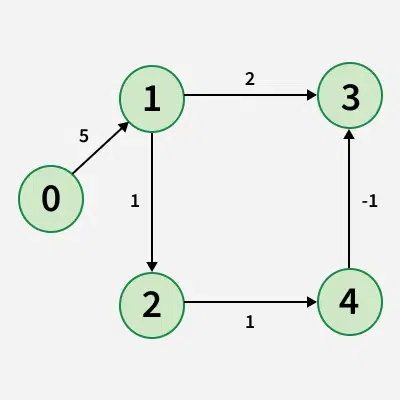
Output: [0, 5, 6, 6, 7]
Input: V = 4, edges = [[0, 1, 4], [1, 2, -6], [2, 3, 5], [3, 1, -2]], src = 0

Output: [-1]
Explanation: The graph contains negative weight cycle.
Negative weight cycle:
A negative weight cycle is a cycle in a graph, whose sum of edge weights is negative. If you traverse the cycle, the total weight accumulated would be less than zero.

Negative Weight Cycle
In the presence of negative weight cycle in the graph, the shortest path doesn’t exist because with each traversal of the cycle shortest path keeps decreasing.
Limitation of Dijkstra’s Algorithm:
Since, we need to find the single source shortest path, we might initially think of using Dijkstra’s algorithm. However, Dijkstra is not suitable when the graph consists of negative edges. The reason is, it doesn’t revisit those nodes which have already been marked as visited. If a shorter path exists through a longer route with negative edges, Dijkstra’s algorithm will fail to handle it.
Bellman-Ford Algorithm – O(V*E) Time and O(V) Space
Bellman-Ford is a single source shortest path algorithm. It effectively works in the cases of negative edges and is able to detect negative cycles as well. It works on the principle of relaxation of the edges.
Principle of Relaxation of Edges
- Relaxation means updating the shortest distance to a node if a shorter path is found through another node. For an edge (u, v) with weight w:
- If going through u gives a shorter path to v from the source node (i.e., distance[v] > distance[u] + w), we update the distance[v] as distance[u] + w.
- In the bellman-ford algorithm, this process is repeated (V – 1) times for all the edges.
Why Relaxing Edges (V – 1) times gives us Single Source Shortest Path?
A shortest path between two vertices can have at most (V – 1) edges. It is not possible to have a simple path with more than (V – 1) edges (otherwise it would form a cycle). Therefore, repeating the relaxation process (V – 1)times ensures that all possible paths between source and any other node have been covered.
Assuming node 0 as the source vertex, let’s see how we can relax the edges to find the shortest paths:

- In the first relaxation, since the shortest paths for vertices 1 and 2 are unknown (infinite), the shortest paths for vertices 2 and 3 will also remain infinite. And, for vertex 1, the distance will be updated to 4, as dist[0] + 4 < dist[1].
- In the second relaxation, the shortest path for vertex 2 is still infinite, which means the shortest path for vertex 3 will also remain infinite. For vertex 2, the distance can be updated to 3, as dist[1] + (-1) = 3.
- In the third relaxation, the shortest path for vertex 3 will be updated to 5, as dist[2] + 2 = 5.
So, in above example, dist[1] is updated in 1st relaxation, dist[2] is updated in second relaxation, so the dist for the last node (V – 1), will be updated in (V – 1)th relaxation.
Detection of a Negative Weight Cycle
- As we have discussed earlier that, we need (V – 1) relaxations of all the edges to achieve single source shortest path. If one additional relaxation (Vth) for any edge is possible, it indicates that some edges with overall negative weight has been traversed once more. This indicates the presence of a negative weight cycle in the graph.
Working of Bellman-Ford Algorithm
C++
// C++ program to find single source shortest path Using Bellman
// -Ford algorithm
#include <iostream>
#include <vector>
using namespace std;
vector<int> bellmanFord(int V, vector<vector<int>>& edges, int src) {
// Initially distance from source to all
// other vertices is not known(Infinite).
vector<int> dist(V, 1e8);
dist[src] = 0;
// Relaxation of all the edges V times, not (V - 1) as we
// need one additional relaxation to detect negative cycle
for (int i = 0; i < V; i++) {
for (vector<int> edge : edges) {
int u = edge[0];
int v = edge[1];
int wt = edge[2];
if (dist[u] != 1e8 && dist[u] + wt < dist[v]) {
// If this is the Vth relaxation, then there is
// a negative cycle
if(i == V - 1)
return {-1};
// Update shortest distance to node v
dist[v] = dist[u] + wt;
}
}
}
return dist;
}
int main() {
int V = 5;
vector<vector<int>> edges = {{1, 3, 2}, {4, 3, -1}, {2, 4, 1},
{1, 2, 1}, {0, 1, 5}};
int src = 0;
vector<int> ans = bellmanFord(V, edges, src);
for (int dist : ans)
cout << dist << " ";
return 0;
}
// Java program to find single source shortest path using
// Bellman-Ford algorithm
import java.util.Arrays;
class GfG {
static int[] bellmanFord(int V, int[][] edges, int src) {
// Initially distance from source to all other vertices
// is not known(Infinite).
int[] dist = new int[V];
Arrays.fill(dist, (int)1e8);
dist[src] = 0;
// Relaxation of all the edges V times, not (V - 1) as we
// need one additional relaxation to detect negative cycle
for (int i = 0; i < V; i++) {
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int wt = edge[2];
if (dist[u] != 1e8 && dist[u] + wt < dist[v]) {
// If this is the Vth relaxation, then there is
// a negative cycle
if (i == V - 1)
return new int[]{-1};
// Update shortest distance to node v
dist[v] = dist[u] + wt;
}
}
}
return dist;
}
public static void main(String[] args) {
int V = 5;
int[][] edges = new int[][] {
{1, 3, 2},
{4, 3, -1},
{2, 4, 1},
{1, 2, 1},
{0, 1, 5}
};
int src = 0;
int[] ans = bellmanFord(V, edges, src);
for (int dist : ans)
System.out.print(dist + " ");
}
}
# Python program to find single source shortest path using
# Bellman-Ford algorithm
def bellmanFord(V, edges, src):
# Initially distance from source to all other vertices
# is not known(Infinite).
dist = [100000000] * V
dist[src] = 0
# Relaxation of all the edges V times, not (V - 1) as we
# need one additional relaxation to detect negative cycle
for i in range(V):
for edge in edges:
u, v, wt = edge
if dist[u] != 100000000 and dist[u] + wt < dist[v]:
# If this is the Vth relaxation, then there
# is a negative cycle
if i == V - 1:
return [-1]
# Update shortest distance to node v
dist[v] = dist[u] + wt
return dist
if __name__ == '__main__':
V = 5
edges = [[1, 3, 2], [4, 3, -1], [2, 4, 1], [1, 2, 1], [0, 1, 5]]
src = 0
ans = bellmanFord(V, edges, src)
print(' '.join(map(str, ans)))
// C# program to find single source shortest path Using Bellman
// -Ford algorithm
using System;
using System.Collections.Generic;
class GfG {
static List<int> BellmanFord(int V, List<List<int>> edges, int src) {
// Initially distance from source to all
// other vertices is not known(Infinite).
List<int> dist = new List<int>(new int[V]);
for (int i = 0; i < V; i++)
dist[i] = (int)1e8;
dist[src] = 0;
// Relaxation of all the edges V times, not (V - 1) as we
// need one additional relaxation to detect negative cycle
for (int i = 0; i < V; i++) {
foreach (List<int> edge in edges) {
int u = edge[0];
int v = edge[1];
int wt = edge[2];
if (dist[u] != 1e8 && dist[u] + wt < dist[v]) {
// If this is the Vth relaxation, then there is
// a negative cycle
if (i == V - 1)
return new List<int> { -1 };
// Update shortest distance to node v
dist[v] = dist[u] + wt;
}
}
}
return dist;
}
static void Main() {
int V = 5;
List<List<int>> edges = new List<List<int>>() {
new List<int> { 1, 3, 2 },
new List<int> { 4, 3, -1 },
new List<int> { 2, 4, 1 },
new List<int> { 1, 2, 1 },
new List<int> { 0, 1, 5 }
};
int src = 0;
List<int> ans = BellmanFord(V, edges, src);
foreach (int dist in ans)
Console.Write(dist + " ");
}
}
// JavaScript program to find single source shortest path Using Bellman
// -Ford algorithm
function bellmanFord(V, edges, src) {
// Initially distance from source to all
// other vertices is not known(Infinite).
let dist = new Array(V).fill(1e8);
dist[src] = 0;
// Relaxation of all the edges V times, not (V - 1) as we
// need one additional relaxation to detect negative cycle
for (let i = 0; i < V; i++) {
for (let edge of edges) {
let u = edge[0];
let v = edge[1];
let wt = edge[2];
if (dist[u] !== 1e8 && dist[u] + wt < dist[v]) {
// If this is the Vth relaxation, then there is
// a negative cycle
if (i === V - 1)
return [-1];
// Update shortest distance to node v
dist[v] = dist[u] + wt;
}
}
}
return dist;
}
let V = 5;
let edges = [
[1, 3, 2],
[4, 3, -1],
[2, 4, 1],
[1, 2, 1],
[0, 1, 5]
];
let src = 0;
let ans = bellmanFord(V, edges, src);
console.log(ans.join(" "));
Time Complexity:
- Best Case: O(E), when distance array after 1st and 2nd relaxation are same , we can simply stop further processing.
- Average Case: O(V*E)
- Worst Case: O(V*E)
Related articles on single source shortest path algorithms: