Expected Value: Random variables are the functions that assign a probability to some outcomes in the sample space. They are very useful in the analysis of real-life random experiments which become complex. These variables take some outcomes from a sample space as input and assign some real numbers to it. The expectation is an important part of random variable analysis. It gives the average output of the random variable.
What is Expected Value?
In mathematics, the expected value (also known as the mean, expectation, or average) of a random variable is a measure of the central tendency or average outcome of that variable over many repetitions of an experiment.
Random Variables and Expectations
Random experiments are those experiments where it is not possible to be certain about the outcomes. In such cases, it is only possible to assign probabilities to the outcomes. Random variables connect the outcomes with a certain real number. For example, consider the experiment of tossing a coin three times. The thing to keep in mind is, a random variable can be defined according to our needs, but the only condition is, that that every outcome of the sample space must be given a value by a random variable.
Types of Random Variables
So, in this case, let R be the random variable, and in this case, it is defined as,
R = Number of heads
Sample Space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
The value given by R for each outcome is shown below in the table.
| Input | Output |
|---|
| R(HHH) | 3 |
| R(HHT) | 2 |
| R(HTH) | 2 |
| R(HTT) | 1 |
| R(THH) | 2 |
| R(THT) | 1 |
| R(TTH) | 1 |
| R(TTT) | 0 |
Notice that more than one outcome can be mapped to a single value by the random variable.
Expectation
For a random variable X, the expectation gives an idea of the average value attained by X when the experiment is repeated many times. Since this value is mapped with an outcome in the sample space. Expected value can be used to determine which of the outcomes is most likely to happen when the experiment is repeated many times.
For random variable X which assumes values x1, x2, x3,…xn with probability P(x1), P(x2), P(x3), … P(xn)
Expectation of X is defined as,
E(x) = 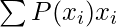
Expected Value
Expectations have a lot of use cases and applications in real life. These concepts are used by insurance companies to compute the probability of death for a person. Expectations are also used in games of chance. For example, while playing poker, or maybe analyzing a lottery system. Analysts use it to compute the probability of winning. This concept is also used in the field of Artificial Intelligence(AI) a lot to understand real-life scenarios and actions.
Properties of Expected Value
Some basic properties of expected values a
- Linearity Principle: For two random variables X and Y => E(X + Y) = E(X) + E(Y)
- For a constant C and a random variable X => E(X + C) = E(X) + C
- For a constant C and a random variable X => E(CX) = C × E(X)
where,
- E(X) and E(Y) represented the value of any variable
- C is Constant
Term Life Insurance and Death Probability
Consider an example, let’s say Akhil has two kids and a wife, and he wants to take an insurance policy for himself so that, in the case of any misshapen, his family won’t have to suffer economically. He buys an insurance policy of 50 lakh rupees. The policy is valid for the next 20 years, which means if something happens to Akhil in the next 10 years, the company will be paying his family 50 lakhs of rupees. These types of policies are called long-term life insurance policies. The condition of this policy is that Akhil will have to pay a premium of Rs 50,000 per year.
How do companies make a profit and calculate the death probability in these cases?
The total amount paid by Akhil in 10 years = Rs 50,000 × 10
= Rs 5,00,000
Insurance Policy = 50,00,000
Ratio becomes 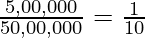 . This means for Rs 10 of insurance they are getting Rs 1 premium. Since they are trying to make profits, they need to get at least 10 Akhils to break even. In that case, out of 10, if only one Akhil dies, the company can break even.
. This means for Rs 10 of insurance they are getting Rs 1 premium. Since they are trying to make profits, they need to get at least 10 Akhils to break even. In that case, out of 10, if only one Akhil dies, the company can break even.
So, if there is a probability of 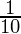 a candidate dying and the company has 10 policyholders, there will be no loss and no profit. Thus, to make a profit
a candidate dying and the company has 10 policyholders, there will be no loss and no profit. Thus, to make a profit
P(Akhil Dying) ≤ 0.1
Getting Data from Expected Value
The expected value gives the central value of the random variable. This is where most of the outputs of the random variables lie when the experiments are repeated many times. These values come in handy while inferring the other variables that are missing most of the time while performing such random experiments. Data can be retrieved using basic algebraic manipulations and expressions for calculating the expected value. The example given below will further clarify this method.
Example: Aman’s dad gave him a die. To check if it was a fair die, he rolled the die 500 times and noted down the frequencies of the values obtained in the table on a piece of paper. Due to rain, some values on the table were washed away. So, instead of doing all the experiments again, he rolled the die 20 times and concluded that the expected value in 20 rolls was 3.37. The washed-away table is given below. Find the values of the missing frequencies.
| Die Value | Absolute Frequency |
|---|
| 1 | A |
| 2 | 110 |
| 3 | 95 |
| 4 | 70 |
| 5 | 75 |
| 6 | B |
| Total | 500 |
Solution:
Assuming that the expected value remains the same in both 20 and 500 trials.
Let’s say the random variable “X” is defined as the value obtained on the die.
X can take values like 1, 2, 3, 4, 5 and 6
The expected value of a random variable is given by,
E(x) = 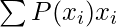
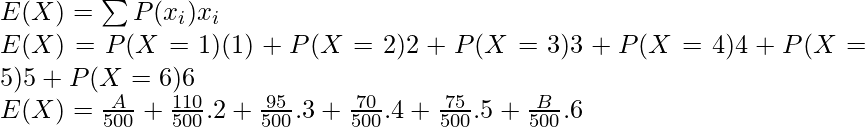
Substituting the expected value,
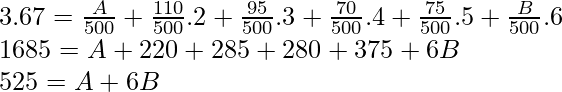
Now this equation has two variables, one more equation is required to solve this.
A + 110 + 95 + 70 + 75 + B = 500
⇒ A+ B = 150
So, the two equations are,
A + B = 150
A + 6B = 525
Solving these equations, the values of variables come out to be.
A =75 and B = 75.
Expected Profit from Lottery Ticket
Expectations can be used to analyze the profits that can be obtained from a lottery ticket. In such games, the chances of winning are little and players usually end up losing money. Through the theory of probability and expectations, the chances and the expected profits can be calculated using which wiser decisions can be made while playing such games.
Example: Asif is playing the lottery in which he has to pick two numbers. If the ticket matches both numbers, he will win the grand prize, which is Rs10005. If only one number matches, he will win a small prize of Rs 1005 and the cost of a lottery ticket is Rs 5. Find the expected profit from the lottery ticket.
Solution :
Suppose Asif draws a lottery ticket “04”. Let X be the random variable which represents profit when the “04” ticket was drawn.
E(X) = P(winning grand prize)(10005 – 5) + P(winning small prize)(1005 – 5) + P(winning nothing)(-5)
Now, the values of these probabilities is required.
P(winning grand prize) = Both the numbers match
= 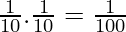
P(winning a small prize) = Only one of the numbers matches
= 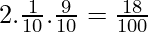
P(winning neither of these prizes) = No one of the numbers matches
= 
Substituting these values,
E(X) = P(winning grand prize)(10005 – 5) + P(winning small prize)(1005 – 5) + P(winning nothing)(-5)
⇒ E(X) = 
⇒ E(X) = 100 + 180 – 4.05
⇒E(X) = 275.95
Expected Value while Fishing
This is yet another example of the use-case of expected value. In this case, there is a bet between two friends who are going fishing. Even before actually fishing, the chances or margins of profit can be analyzed using the expectations of random variables. The below example shows one such incident of bets between two friends who went fishing and placed bets on fish.
Example: Two friends are fishing in a pond that contains 10 trout and 10 sunfish. Each time they catch a fish, they release it back immediately. They made a bet. If the next three fishes friend A catches are all sunfish, then friend B will pay him Rs 100, otherwise, friend A will have to pay Rs 20 to B. Find the expected profit from the bet.
Solution:
Let X be a random variable denoting the profit from the bet.
E(X) = P(A catches all three sunfish)(100) + P(A cannot catch all three sunfish)(-20)
Computing the probabilities,
P(A catches all three sunfish) = 
P(A doesn’t catch all three sunfish) = 1 – P(A catches all three sunfish)
= 1 – 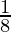
= 
Substituting the values computed above into the expectation equation,
E(X) = P(A catches all three sunfish)(100) + P(A cannot catch all three sunfish)(-20)
⇒ E(X) = P(A catches all three sunfish)(100) + P(A cannot catch all three sunfish)(-20)
⇒ E(X) = 
⇒ E(X) = 
Comparing Insurance with Expected Value
Insurance companies show a lot of plans and try to lure customers to buy them. Not all the plans are beneficial to customers. One such case is medical insurance. A lot of insurance companies, to make more profit, make attractive schemes that are not beneficial in the long term. In such cases, it becomes essential to use the expectations and calculate the expected medical costs. Such methods usually help in differentiating between plans and making a wise decision about medical insurance. To get a better idea about this case, let’s consider the example given below.
Example: Vasu wants to buy a medical insurance plan, but he is confused between plan A and plan B.
Plan A: This is a low deductible plan, he will have to pay the first 10,000 rupees of any medical costs. Additionally, to cover the plan, he will have to pay Rs 80,000 per year.
Plan B: This is a high-deductible plan, he will have to pay the first 25,000 rupees of any medical costs. Additionally, to cover the plan, he will have to pay Rs 60,000 per year.
Find the expected cost for both plans and help Vasu decide. A table is given which gives the stats about the probability of these medical expenses.
| Medical Cost | Probability |
|---|
| Rs 0 | 30 % |
| Rs 10000 | 25 % |
| Rs 40,000 | 20 % |
| Rs 70,000 | 20 % |
| Rs 1,50,000 | 5 % |
Solution:
Let random variable X define the expected cost,
Expected value for Plan A:
E(X) = 80,000 + 0 (0.3) + 10000(0.25) + 10000(0.2) + 10000(0.2) + 10000(0.05)
⇒ E(X) = 80,000 + 2500 + 2000 + 2000 + 500
⇒ E(X) = 87000
Expected value for plan B:
E(X) = 60,000 + 0 (0.3) + 10000(0.25) + 25000(0.2) + 25000(0.2) + 25000(0.05)
⇒ E(X) = 60,000 + 2500 + 5000 + 5000 + 1250
⇒ E(X) = 73,750
Expected expenses are most in plan A. Thus, Vasu should take plan B.
Expected Value – Solved Examples
Problem 1: Find the expected value of the outcome when a die is rolled.
Solution:
Consider X is a random variable that represents the value that comes when a die is rolled.
X = {1, 2, 3, 4, 5, 6}
Now, since the die is a fair die, the probability of getting each outcome is equal. That is 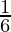
E(X) = 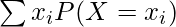
⇒ E(X) = P(X = 1)(1) + P(X = 2)(2) + P(X = 3)(3) + P(X = 4)(4) + P(X = 5)(5) + P(X = 6)(6)
⇒ E(X) = 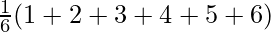
⇒ E(X) = 3
Problem 2: A company makes phones. Out of 100 phones, one is faulty. For each phone, the company makes a profit of Rs2,000 and a loss of Rs 10,000 for the faulty phone. Find the expected profit.
Solution:
Let X be expected profit
E() = 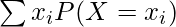
⇒ E(X) = P(X = Phone is working)(2000) + P(X = faulty phone)(10,000)
⇒ E(X) = 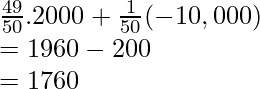
⇒ E(X) = 1760
Problem 3: In a three-time coin toss experiment. Find the expected number of heads.
Solution:
Let X be the number of heads obtained
Sample Space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
E() = 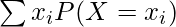
⇒ E(X) =P(X = 0)(0) + P(X = 1)(1) + P(X =2)(2) + P(X = 3)(3)
Finding out the probabilities,
P(X = 0) = 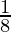
P(X = 1) = 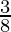
P(X = 2) = 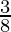
P(X = 3) = 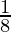
⇒ E(X) = P(X = 0)(0) + P(X = 1)(1) + P(X =2)(2) + P(X = 3)(3)
⇒ E(X) = 
⇒ E(X) =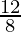
⇒ E(X) = 1.5
Problem 4: Two friends are fishing in a pond that contains 5 trout and 5 sunfish. Each time they catch a fish, they release it back immediately. They made a bet. If the next three fishes friend A catches are all sunfish, then friend B will pay him Rs 10, otherwise, friend A will have to pay Rs 2 to B. Find the expected profit from the bet.
Solution:
Let X be a random variable denoting the profit from the bet.
E(X) = P(A catches all three sunfish)(10) + P(A cannot catch all three sunfish)(-2)
Computing the probabilities,
P(A catches all three sunfish) = 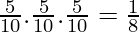
P(A doesn’t catch all three sunfish) = 1 – P(A catches all three sunfish)
= 1 – 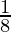
= 
Substituting the values computed above into the expectation equation,
E(X) = P(A catches all three sunfish)(10) + P(A cannot catch all three sunfish)(-2)
⇒ E(X) = P(A catches all three sunfish)(10) + P(A cannot catch all three sunfish)(-2)
⇒ E(X) = 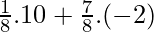
⇒ E(X) = 
Problem 5: Find the expected value of the outcome when a die is rolled. Given that the die is not fair, the probability of getting a 6 is 0.4 and the rest of the numbers are equally likely.
Solution:
Consider X is a random variable that represents the value that comes when a die is rolled.
X = {1, 2, 3, 4, 5, 6}
Now, since the die is not fair die,
P(6) = 0.4
P(1) = P(2) = P(3) = P(4) = P(5) = 0.12
E(X) = 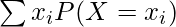
⇒ E(X) = P(X = 1)(1) + P(X = 2)(2) + P(X = 3)(3) + P(X = 4)(4) + P(X = 5)(5) + P(X = 6)(6)
⇒ E(X) = (0.12)(1) + (0.12)(2) + (0.12)(3) + (0.12)(4) + (0.12)(5) + (0.4)(6)
⇒ E(X) = (0.12)(1 + 2 + 3+ 4+ 5) + 2.4
⇒ E(X) = 1.8 + 2.4
⇒E(X) = 4.2
Summary – Expected Value
Random variables play a crucial role in analyzing uncertain outcomes by assigning probabilities to events in a sample space. They connect outcomes with real numbers and are pivotal in determining the average outcome, known as the expectation. Expectation provides insight into the most likely outcome over repeated experiments. Applications of random variables and expectations range from insurance risk assessment to analyzing games of chance and even guiding decision-making in fields like Artificial Intelligence. Understanding the properties and calculations of expected values aids in making informed choices and predicting outcomes in uncertain scenarios.
FAQs on Expected Value
What is the significance of random variables in probability theory?
Random variables serve as mathematical tools to model uncertain events or outcomes in probability theory. They map outcomes from a sample space to real numbers, allowing us to quantify and analyze the likelihood of different events occurring.
How does the expectation of a random variable help in decision-making processes?
The expectation of a random variable provides a measure of the average outcome or value that can be expected over many repetitions of an experiment.
Can you explain the linearity principle of expected values and its importance?
The linearity principle states that the expected value of the sum of two random variables is equal to the sum of their individual expected values.
Similar Reads
Probability in Maths
Probability is a field of mathematics that deals with events and quantifies their likelihood of occurring with numerical values ranging from 0 to 1. Higher probabilities indicate a greater chance of the event happening. It is mainly a ratio between the given event and the total number of events. Wha
3 min read
Events in Probability
Events in Probability- In Probability, an event can be defined as any outcome or set of outcomes from a random experiment. In other words, an event in probability is the subset of the respective sample space. Example:1. If you roll a die, the event could be "getting a 3" or "getting an even number."
14 min read
Probability Based on Coin
How to calculate Dice Probabilities?
Probability is also known as a possibility, which works in the happening of a likely event. The utility is designated from zero to one. In math, Probability has been obvious to approximate how possible events are to occur. Basically, the probability is the scope to which something is to be expected
6 min read
Axiomatic Approach to Probability
Hearing the word "probability" brings up ideas related to uncertainty or randomness. Although the concept of probability can be hard to describe formally, it helps us analyze how likely it is that a certain event will happen. This analysis helps us understand and describe many phenomena we see in re
10 min read
Addition Rule for Probability
Probability is an experimental approach to the game of chances we come across every day in our lives. It is a way to describe these “chances” mathematically and then analyze them. It allows us to measure the chances of something occurring. Probability of Event P(E) = [Number of Favorable Outcomes] /
10 min read
Conditional Probability
Conditional probability is one type of probability in which the possibility of an event depends upon the existence of a previous event. Conditional probability is the likelihood of an outcome occurring based on a previous outcome in similar circumstances. In probability notation, this is denoted as
15+ min read
Bayes' Theorem
Bayes' Theorem is used to determine the conditional probability of an event. It is used to find the probability of an event, based on prior knowledge of conditions that might be related to that event. Bayes' Theorem and Conditional ProbabilityBayes theorem (also known as the Bayes Rule or Bayes Law)
11 min read
Multiplication Theorem
Probability refers to the extent of the occurrence of events. When an event occurs like throwing a ball, picking a card from the deck, etc ., then there must be some probability associated with that event. In terms of mathematics, probability refers to the ratio of wanted outcomes to the total numbe
8 min read
Dependent and Independent Events
Dependent and Independent Events are the types of events that occur in probability. Suppose we have two events say Event A and Event B then if Event A and Event B are dependent events then the occurrence of one event is dependent on the occurrence of other events if they are independent events then
8 min read
Discrete Random Variable
Discrete Random Variables are an essential concept in probability theory and statistics. Discrete Random Variables play a crucial role in modelling real-world phenomena, from the number of customers who visit a store each day to the number of defective items in a production line. Understanding discr
15 min read
Probability Distribution - Function, Formula, Table
A probability distribution describes how the probabilities of different outcomes are assigned to the possible values of a random variable. It provides a way of modeling the likelihood of each outcome in a random experiment. While a frequency distribution shows how often outcomes occur in a sample or
15+ min read
Measures of Dispersion | Types, Formula and Examples
Measures of Dispersion are used to represent the scattering of data. These are the numbers that show the various aspects of the data spread across various parameters. Let's learn about the measure of dispersion in statistics , its types, formulas, and examples in detail. Dispersion in StatisticsDisp
10 min read
Expected Value
Expected Value: Random variables are the functions that assign a probability to some outcomes in the sample space. They are very useful in the analysis of real-life random experiments which become complex. These variables take some outcomes from a sample space as input and assign some real numbers t
15+ min read
Bernoulli Trials and Binomial Distribution
Bernoulli Trials and Binomial Distribution are the fundamental topics in the study of probability and probability distributions. Bernoulli's Trials are those trials in probability where only two possible outcomes are Success and Failure or True and False. Due to this fact of two possible outcomes, i
13 min read
Binomial Distribution in Probability
Binomial Distribution is a probability distribution used to model the number of successes in a fixed number of independent trials, where each trial has only two possible outcomes: success or failure. This distribution is useful for calculating the probability of a specific number of successes in sce
15 min read
What is Binomial Probability Distribution with Example?
In a binomial distribution, the probability of achieving success must stay consistent across the trials being examined. For instance, when tossing a coin, the probability of landing heads is always ½ for each trial, as there are only two possible outcomes.Explanation: Probability is the likelihood o
6 min read
Probability Distribution Function
Probability Distribution refers to the function that gives the probability of all possible values of a random variable.It shows how the probabilities are assigned to the different possible values of the random variable.Common types of probability distributions Include: Binomial Distribution.Bernoull
9 min read