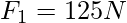Hydraulic Machines

Hydraulic machines are used in a lot of mechanical devices, from our cars to the springs used in trains. Hydraulic systems are involved. These systems are based upon a very basic principle but are very effective. These systems can be used to lift very heavy weights which will otherwise be impossible to lift. Hydraulic machines are based on pressure. It is essential to understand these systems to get an overview of complex machinery that is used all around us. Let’s look at this concept in detail. 

Pascal’s Law 

French scientist Blaise Pascal observed that pressure in a fluid at rest is the same at all points if these points are at the same depth. The figure below shows a cylindrical element in the fluid of area A and height h. Let the pressure at the top of the element be P₁ and P₂ at the bottom. Let us assume that the weight of the liquid is “mg” in this element. Then the difference in pressures between the two points is given by, 

P₁ – P₂ = mgh/A

Now, assuming the density of the liquid to be “d”, then the mass of the liquid in the element will be, 

m = d(A.h) 

⇒ m = d.A.h

Plugging this value of m in the above equation for the pressure difference, 

P₁ – P₂ = dgh

This extra pressure with the height “h” is called gauge pressure. 

Hydraulic Machines

Let’s see what happens when we change the pressure on the liquid. According to Pascal’s law of transmission, whenever external pressure is applied to any part of a liquid. This pressure gets distributed in all directions equally. A number of devices are based on this principle. The hydraulic lift is also an application of this law. Consider a hydraulic lift as given in the figure below. The two pistons are separated by a space filled with liquid. A piston of small cross-section A₁ is used to exert a force F₁ directly on the liquid. 

The pressure that is exerted in the column is given by, P =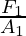. This is transmitted throughout the liquid, which results in the pressure being applied on the other piston. The area of the other piston is A₂, the force felt by this piston is given by, 

⇒ 

⇒ 

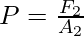
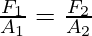
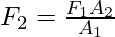
Notice that the applied force is increased by the factor of 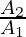. This property helps in hydraulic systems for lifting very heavyweights. 

Sample Problems 

Question 1: Hydraulic Machines work on the application of: 

1. Pascal’s Law 
2. Newton’s Law 
3. Law of Gravity 
4. None of These 

Answer:

Hydraulic Machines are based on the Pascal’s law of transmission. It says, 

Whenever external pressure is applied to any part of a liquid. This pressure gets distributed in all directions equally.

Thus, answer is (1) 

Question 2: Find the pressure difference that comes when someone goes 10m deep inside the water. Given, the density of water = 1000Kg/m³. 

Answer:

The difference between the pressures is given by, 

P₁ – P₂ = dgh

Given: d = 1000, g = 10 and h = 10

P₁ – P₂ = dgh

⇒P₁ – P₂ = (1000)(10)(10) 

⇒P₁ – P₂ = 10⁵ Kg/m²

Question 3: Find the pressure difference that comes when someone goes 50m deep inside a liquid. Given the density of water = 500Kg/m³. 

Answer:

The difference between the pressures is given by, 

P₁ – P₂ = dgh

Given: d = 500, g = 10 and h = 50

P₁ – P₂ = dgh

⇒P₁ – P₂ = (500)(10)(50) 

⇒P₁ – P₂ = 25 × 10³ Kg/m²

Question 4: A hydraulic piston has two ends of the area A₁ = 1m² and A₂ = 0.2m². A Force of 100N is applied on the piston with a smaller area. Find the force on the other end.

Answer:

In a hydraulic system, the force on the other end is given by, 

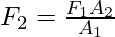
Given: A₁ = 1m² and A₂ = 0.2m². F₁ = 100N

Plugging the values in the equation, 

⇒ 

⇒ 

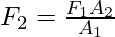
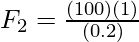
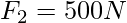
Question 5: A hydraulic piston has two ends of the area A₁ = 0.5m² and A₂ = 0.1m². A Force of 50N is applied on the piston with a smaller area. Find the force on the other end.

Answer:

In a hydraulic system, the force on the other end is given by, 

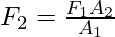
Given: A₁ = 0.1m² and A₂ = 0.5m². F₁ = 50N

Plugging the values into the equation, 

⇒ 

⇒ 

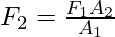
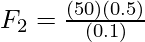
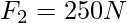
Question 6: A hydraulic piston has two ends of the area A₁ = 0.4m² and A₂ = 0.1m². The goal is to pick the 50Kg box kept on the piston with 0.4 m² area. , find the force that should be applied at the other end. 

Answer:

In a hydraulic system, the force on the other end is given by, 

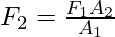
Given: A₁ = 0.1m² and A₂ = 0.5m². F₂ = 500N

Plugging the values into the equation, 

⇒ 

⇒ 

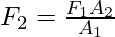
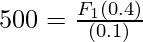
A

anjalishukla1859

Follow

Improve