Introduction To Grammar in Theory of Computation

Last Updated : 28 Dec, 2024

In the context of the Theory of Computation, grammar refers to a formal system that defines how strings in a language are structured. It plays a crucial role in determining the syntactic correctness of languages and serves as a foundation for parsing and interpreting programming languages, natural languages, and various formal systems. This article provides an in-depth look at the types of grammars, their components, and the derivation of strings from grammars.

What is Grammar in Computation?

Grammar is a formal system that defines a set of rules for generating valid strings within a language. It serves as a blueprint for constructing syntactically correct sentences or meaningful sequences in a formal language.

Grammar is basically composed of two basic elements:

Terminal Symbols: Terminal symbols are those that are the components of the sentences generated using grammar and are represented using small case letters like a, b, c, etc.
Non-Terminal Symbols: Non-terminal symbols are those symbols that take part in the generation of the sentence but are not the component of the sentence. Non-Terminal Symbols are also called Auxiliary Symbols and Variables. These symbols are represented using a capital letters like A, B, C, etc.

Representation of Grammar

Any Grammar can be represented by 4 tuples – <N, T, P, S>

N – Finite Non-Empty Set of Non-Terminal Symbols.
T – Finite Set of Terminal Symbols.
P – Finite Non-Empty Set of Production Rules.
S – Start Symbol (Symbol from where we start producing our sentences or strings).

Production Rules

A production or production rule in computer science is a rewrite rule specifying a symbol substitution that can be recursively performed to generate new symbol sequences. It is of the form α-> β where α is a Non-Terminal Symbol which can be replaced by β which is a string of Terminal Symbols or Non-Terminal Symbols.

Example-1: Consider Grammar G1 = <N, T, P, S>

T = {a,b} #Set of terminal symbols
P = {A->Aa,A->Ab,A->a,A->b,A-> [Tex]\epsilon[/Tex]} #Set of all production rules
S = {A} #Start Symbol

As the start symbol is S then we can produce Aa, Ab, a,b,[Tex]\epsilon [/Tex]which can further produce strings where A can be replaced by the Strings mentioned in the production rules and hence this grammar can be used to produce strings of the form (a+b)*.

Derivation of Strings

A->a #using production rule 3
OR
A->Aa #using production rule 1
Aa->ba #using production rule 4
OR
A->Aa #using production rule 1
Aa->AAa #using production rule 1
AAa->bAa #using production rule 4
bAa->ba #using production rule 5

Example-2: Consider Grammar G2 = <N, T, P, S>

N = {A} #Set of non-terminals Symbols
T = {a} #Set of terminal symbols
P = {A->Aa, A->AAa, A->a, A->[Tex]\epsilon[/Tex]} #Set of all production rules
S = {A} #Start Symbol

As the start symbol is S then we can produce Aa, AAa, a,[Tex]\epsilon [/Tex]which can further produce strings where A can be replaced by the Strings mentioned in the production rules and hence this grammar can be used to produce strings of form (a)*.

Derivation of Strings

A->a #using production rule 3
OR
A->Aa #using production rule 1
Aa->aa #using production rule 3
OR
A->Aa #using production rule 1
Aa->AAa #using production rule 1
AAa->Aa #using production rule 4
Aa->aa #using production rule 3

Equivalent Grammars

Two grammars are said to be equivalent if they generate the same language. For instance, if Grammar 1 and Grammar 2 both generate strings of the form (𝑎+𝑏)∗, they are considered equivalent.

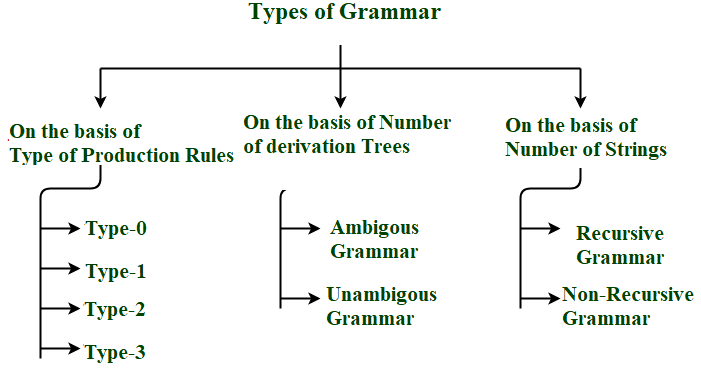
Types of Grammars

There are several types of Grammar. We classify them on the basis mentioned below.

Type of Production Rules: The form and complexity of the production rules define the grammar type, such as context-free, context-sensitive, regular, or unrestricted grammars.
Number of Derivation Trees: The number of ways a string can be derived from the grammar. Ambiguous grammars have multiple derivation trees for the same string.
Number of Strings: The size and nature of the language generated by the grammar.

Types of Grammar

Conclusion

Grammar is the foundation of understanding languages in computation. It provides a structured way of generating strings that belongs to a specific language. From programming languages to natural language processing, formal grammars are critical in ensuring that the sentences (or strings) formed are syntactically correct.