Logarithmic Differentiation

Last Updated : 17 Dec, 2024

Method of finding a function’s derivative by first taking the logarithm and then differentiating is called logarithmic differentiation. This method is specially used when the function is type y = f(x)^g(x). In this type of problem where y is a composite function, we first need to take a logarithm, making the function log (y) = g(x) log (f(x)).

Logarithmic Differentiation helps to find the derivatives of complicated functions, using the concept of logarithms. Sometimes finding the differentiation of the function is very tough but differentiating the logarithm of the same function is very easy, then in such cases, the logarithmic differentiation formula is used.

Note: Logarithmic differentiation is generally used to differentiate functions of form f(x)g(x), f(x)/g(x), f(x)^g(x), and others.

Formula for Logarithmic Differentiation

For a function, y = f(x)^g(x), differentiation is given by the following formula:

$\bold{\frac{dy}{dx} = y\left[g(x)\cdot \frac{f'(x)}{f(x)} + log(f(x))g'(x)\right]}$

Logarithmic formulas are very useful in solving logarithmic differentiation. Some of the important logarithmic properties used are,

log XY = log X + log Y
log X/Y = log X – log Y
log X^Y = Y log X
log_Y X = (log X) / (log Y)

Note: Logarithmic differentiation rules are only valid for the positive functions only because logarithm of negative function is undefined.

Derivation of Logarithmic Differentiation Formula

Let us consider a function y = f(x)^g(x), and take the natural logarithm of this function to differentiate it,

ln y = ln (f(x)^g(x))
⇒ ln (y) = g(x) ln (f(x))

Differentiate the above equation,

$\frac{d [\ln y]}{dx} = \frac{d}{dx}[g(x) \cdot \ln f(x)$
$\Rightarrow \frac{1}{y} \cdot \frac{dy}{dx} = g'(x) \ln(f(x)) + g(x) \cdot \frac{d}{dx}(\ln(f(x)))$
$\Rightarrow \frac{dy}{dx} = y \left(g'(x) \ln(f(x)) + g(x) \cdot \frac{d}{dx}(\ln(f(x)))\right)$
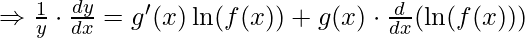
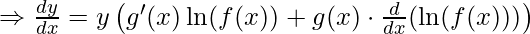
$\Rightarrow \frac{dy}{dx} = y \left[g'(x) \ln(f(x)) + g(x) \cdot \frac{f'(x)}{f(x)}\right]$

Which is the required formula.

How to Perform Logarithmic Differentiation?

The steps involved in differentiating a logarithmic function are summarized below,

Take log on both sides,
Use logarithmic properties to simplify the function,
Now differentiate the equation with respect to x,
Simplify the obtained equation,
Substitute back the value of y.

Following the above result one can easily find the differentiation of functions using logarithm.

Let’s consider an example for better understanding.

Example: Find the derivative of x^x.

Solution:

Let y = x^x

Step 1: Taking log on both sides
log(y) = log(x^x)

Step 2: Use logarithmic property to simplify the equation
log(y) = x ⋅ log(x) [Using property log(a^b) = b⋅ log(a)]

Step 3: Now differentiate the equation with respect to x,
$\frac{d}{d x} \log (y)=\frac{d}{d x}(x \cdot \log (x)) \\ \frac{d}{d x} \log (y)=x \cdot \frac{d}{d x} \log (x)+\log (x) \cdot \frac{d x}{d x} \\ \frac{1}{y} \frac{d y}{d x}=x \cdot \frac{1}{x}+\log (x)$

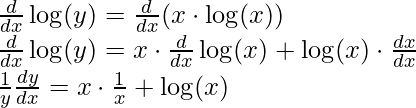
Step 4: Simplify the obtained equation
$\frac{d y}{d x}=y(1+\log (x))$

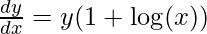
Step 5: Substitute back the value of y
$\frac{d y}{d x}=x^{x}(1+\log (x))$

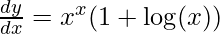
Applications of Log Differentiation

Log differentiation found its application while solving various differentiation problems. Various types of problems where Log Differentiation is used are discussed below,

Product of Functions (Product Rule)

The differentiation of any function which is a product of two functions can easily be calculated using logarithmic differentiation.

Suppose we have to find differentiation of f(x) where, f(x) = g(x) × h(x) then by using concept of logarithmic differentiation,

f(x) = g(x) × h(x)

Taking log on both sides,

log f(x) = log (g(x) × h(x))
⇒ log f(x) = log g(x) + log h(x) [Using property log (XY) = log (X) + log (Y)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [log g(x)] + d/dx [log h(x)]
⇒ f'(x)/f(x) = g'(x)/g(x) + h'(x)/h(x)
⇒ f'(x) = f(x) [g'(x)/g(x) + h'(x)/h(x)]
⇒ f'(x) = f(x) [(h(x) × g'(x) + g(x) × h'(x))/ (g(x) × h(x))]
⇒ f'(x) = g(x) × h(x) [h(x) × g'(x) + g(x) × h'(x)] / g(x) × h(x)

∴ f'(x) = h(x) × g'(x) + g(x) × h'(x)

The result obtained above is the “Leibniz rule” and is commonly known as the “Product rule“.

Division of Functions (Quotient Rule)

The differentiation of any function which is in the form of a division of two functions can easily be calculated using logarithmic differentiation.

Suppose one has to find the differentiation of f(x) where f(x) = g(x) / h(x) by using the concept of logarithmic. differentiation,

f(x) = g(x)/h(x)

Taking log on both sides,

log f(x) = log [g(x)/h(x)]
⇒ log f(x) = log g(x) – log h(x) [Using property log (X/Y) = log (X) – log (Y)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [log g(x)] – d/dx [log h(x)]
⇒ f'(x)/f(x) = g'(x)/g(x) – h'(x)/h(x)
⇒ f'(x) = f(x)[g'(x)/g(x) – h'(x)/h(x)]
⇒ f'(x) = f(x) [(g'(x) × h(x) – g(x) × h'(x))/(g(x) × h(x))]
⇒ f'(x) = g(x)/h(x) [g'(x) × h(x) – g(x) × h'(x)]/g(x) × h(x)

∴ f'(x) = [g'(x) × h(x) – g(x) × h'(x)] / h²(x)

The result obtained above is commonly known as the “Quotient rule“.

Also, Check

Solved Examples on Logarithmic Differentiation

Example 1: Find the derivative of 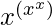$x^{\left(x^{x}\right)}$ ?

Solution:

Given, y = 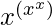$x^{\left(x^{x}\right)}$

Step 1: Taking log on both sides,
log(y) = log(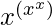 $x^{\left(x^{x}\right)}$ )

Step 2: Use logarithmic property to simplify the equation
log(y) = x^x⋅ log(x) [Using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,
$\frac{d}{d x} \log (y)=\frac{d}{d x}\left(x^{x} \cdot \log (x)\right) \\ \frac{d}{d x} \log (y)=x^{x} \cdot \frac{d}{d x} \log (x)+\log (x) \cdot \frac{d}{d x} x^{x}\left\{f^{\prime}(u . v)=u . f^{\prime}(v)+v \cdot f^{\prime}(u)\right\} \\ \frac{1}{y} \frac{d y}{d x}=x^{x} \cdot \frac{1}{x}+\log (x) \frac{d}{d x} x^{x} \left\{f^{\prime}(\log x)=\frac{1}{x}\right\}\\ \frac{1}{y} \frac{d y}{d x}=x^{x-1}+\log (x) \frac{d}{d x} x^{x}$

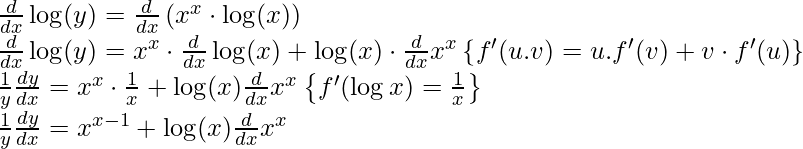
Step 4: Simplify the obtained equation,

Since now we know the derivative of x^x, We will substitute here directly.
$\frac{1}{y} \frac{d y}{d x}=x^{x-1}+\log x \cdot x^{x}(1+\log x) \\ \frac{d y}{d x}=y\left(x^{x-1}+\log x \cdot x^{x}(1+\log x)\right)$

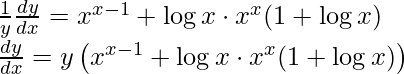
Step 5: Substitute back the value of y
$\frac{d y}{d x}=x^{\left(x^{x}\right)}\left(x^{x-1}+\log x \cdot x^{x}(1+\log x)\right)$

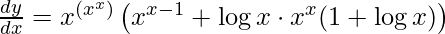
Example 2: Find the derivative of y = (log x)^x.

Solution:

Given, y = (logx)^x

Step 1: Taking log on both sides,
log(y) = log((logx)^x)

Step 2: Use logarithmic property to simplify the equation
log(y) = x ⋅ log(logx) [using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,
$\frac{d}{d x} \log (y)=\frac{d}{d x}(x \cdot \log (\log x)) \\ \frac{d}{d x} \log (\mathrm{y})=x \cdot \frac{d}{d x} \log (\log x)+\log (\log x) \cdot \frac{d x}{d x} \\ \frac{1}{y} \frac{d y}{d x}=x \cdot \frac{1}{\log x} \cdot \frac{1}{x}+\log (\log x)$

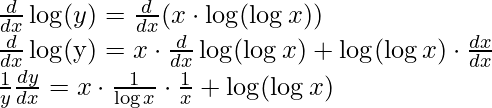
Step 4: Simplify the obtained equation,
$\frac{1}{y} \frac{d y}{d x}=\frac{1}{\log x}+\log (\log x) \{ using~chain~rule \} \\ \frac{d y}{d x}=y \cdot\left(\frac{1}{\log x}+\log (\log x)\right) \\$

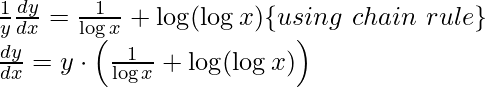
Step 5: Substitute back the value of y
$\frac{d y}{d x}=(\log x)^{x} \cdot\left(\frac{1}{\log x}+\log (\log x)\right)$

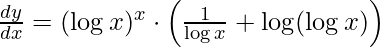
Example 3: Find the derivative of y = x^√x.

Solution:

Given, y = x^√x

Step 1: Taking log on both sides,
log(y) = log(x^√x)

Step 2: Use logarithmic property to simplify the equation
log(y) = √x⋅ log(x) [using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,
$\frac{d}{d x} \log (y)=\frac{d}{d x}(\sqrt{x} \cdot \log (x))\\ \frac{d}{d x} \log (\mathrm{y})=\sqrt{x} \cdot \frac{d}{d x} \log (\mathrm{x})+\log (x) \cdot \frac{d \sqrt{x}}{d x}$

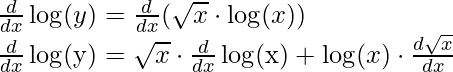
Step 4: Simplify the obtained equation,
$\frac{1}{y} \frac{d y}{d x}=\sqrt{x} \cdot \frac{1}{x}+\log (x) \cdot \frac{1}{2 \sqrt{x}} \\ \frac{1}{y} \frac{d y}{d x}=\frac{1}{\sqrt{x}}+\log (x) \cdot \frac{1}{2 \sqrt{x}} \\ \frac{d y}{d x}=y \cdot\left(\frac{1}{\sqrt{x}}+\log (\mathrm{x}) \cdot \frac{1}{2 \sqrt{x}}\right) \\$

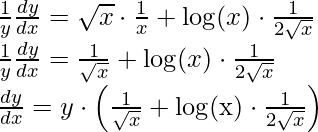
Step 5: Substitute back the value of y
$\frac{d y}{d x}=\mathrm{x}^{\sqrt{x}} \cdot\left(\frac{1}{\sqrt{x}}+\log (\mathrm{x}) \cdot \frac{1}{2 \sqrt{x}}\right)$

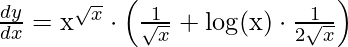
Practice Questions on Logarithmic Differentiation

Q1: Differentiate the function y = (sin x)^{cos x} with respect to x.

Q2: Find the derivative of the function y = (log x)^{log x} with respect to x.

Q3: Differentiate the function y = (x² + 1)^{x – 1} with respect to x.

Q4: Find the derivative of the function y = (tan x)^{cot x} with respect to x.

Q5: Differentiate the function y = (e^x)^x with respect to x.

Answer Key

$\frac{dy}{dx} = (\sin x)^{\cos x} \left( -\sin x \ln(\sin x) + \cos x \cot x \right)$
$\frac{dy}{dx} = (\log x)^{\log x} \left( \frac{\ln(\log x)}{x} + \frac{1}{x} \right)$
$\frac{dy}{dx} = (x^2 + 1)^{x - 1} \left( \ln(x^2 + 1) + \frac{2x(x - 1)}{x^2 + 1} \right)$
$\frac{dy}{dx} = (\tan x)^{\cot x} \left( -\csc^2 x \ln(\tan x) + \cot x \cdot \frac{\sec^2 x}{\tan x} \right)$
$\frac{dy}{dx} = e^{x \ln x} \left( \ln x + 1 \right)$

FAQs on Logarithmic Differentiation

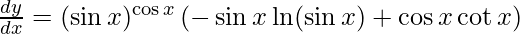
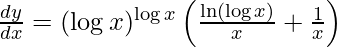
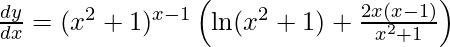
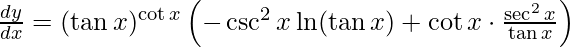
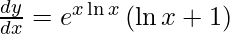
What is the Formula of Logarithmic Differentiation?

Logarithmic Differentiation of a function f(x) is found by dividing the differentiation of the function by the function itself. i.e.

d/dx [log f(x)] = f ‘(x)/f(x)

Logarithmic differentiation of a function is calculated using the chain rule of differentiation. These functions are also used to solve exponential functions.

When Logarithmic Differentiation is used?

Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of another function, etc. Logarithmic differentiation solves such types of complex functions very easily.

What are the Examples of Log Differentiation?

Logarithmic differentiation is used to solve different functions, such as, exponential e^{cos x}, product (x + 5)³ (x² + 2)³, exponent (cos x)^{sin x} , etc.

What are the Different Rules of Logarithmic Differentiation?

Logarithmic differentiation uses the following rules to obtain the differentiation of the complex functions, such as,

Product Rule
Quotient Rule
Exponential Rule

Log Table | How to Use Logarithm Table with Examples

rathoreatul27

Improve

Article Tags :

Logarithmic Differentiation

Formula for Logarithmic Differentiation

Derivation of Logarithmic Differentiation Formula

How to Perform Logarithmic Differentiation?

Applications of Log Differentiation

Product of Functions (Product Rule)

Division of Functions (Quotient Rule)

Solved Examples on Logarithmic Differentiation

Practice Questions on Logarithmic Differentiation

Answer Key

FAQs on Logarithmic Differentiation

What is the Formula of Logarithmic Differentiation?

When Logarithmic Differentiation is used?

What are the Examples of Log Differentiation?

What are the Different Rules of Logarithmic Differentiation?

Similar Reads

What kind of Experience do you want to share?