Functions are defined as the relations which give a particular output for a particular input value. A function has a domain and codomain (range). f(x) usually denotes a function where x is the input of the function. In general, a function is written as y = f(x).
What is a Function?
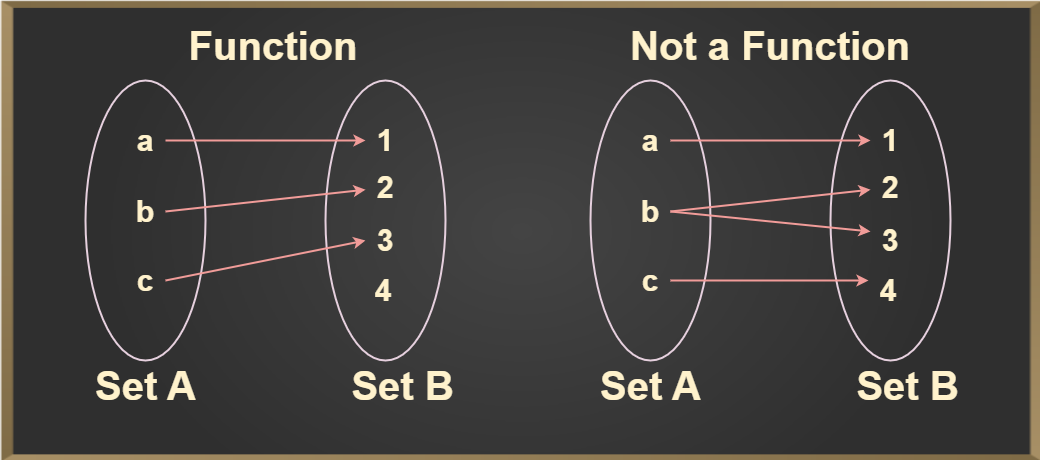
A function is a relation between two sets set A and set B. Such that every element of set A has an image in set B and no element in set A has more than one image in set B.
Let A and B be two nonempty sets. A function or mapping f from A to B is written as f: A → B is a rule by which each element a ∈ A is associated with a unique element b ∈ B.
Domain, Codomain, and Range of a Function
The elements of set X are called the domain of f and the elements of set Y are called the codomain of f. The images of the elements of set X are called the range of function, which is always a subset of Y. The image given below demonstrates the domain, codomain, and range of the function.
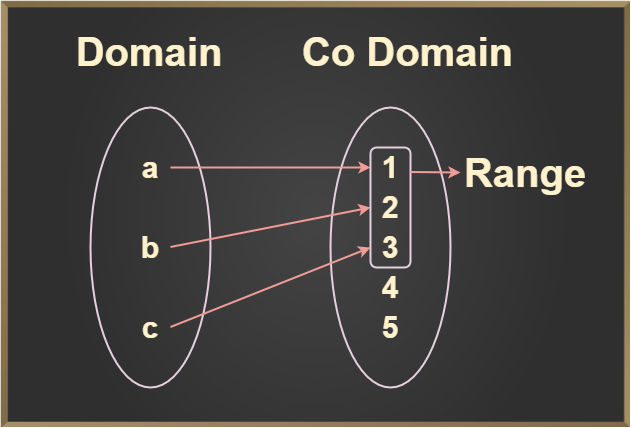
The image demonstrates the domain, co-domain, and range of the function. Remember the element which is mapped only will be counted in the range as shown in the image. The domain, codomain, and range of the above function are:
Domain = {a, b, c}
Codomain = {1, 2, 3, 4, 5}
Range = {1, 2, 3}
Read More about Domain and Range.
Types of Functions in Maths
An example of a simple function is f(x) = x3. In this function, f(x) takes the value of “x” and then cubes it to find the value of the function. For example, if the value of x is taken to be 2, then the function gives 8 as output i.e. f(2) = 8.
Some other examples of functions are:
f(x) = cos x, f(x) = 5x2 + 9, f(x) = 1/x3, etc.
There are several types of functions in maths. Some of the important types are:
- One to One (Injective) function
- Many to One function
- Onto (Surjective) Function
- Into Function
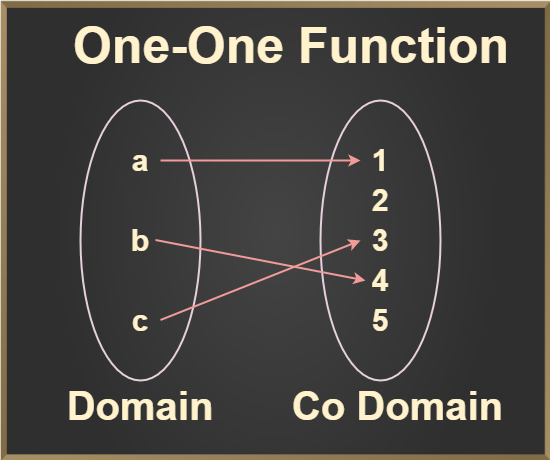
One to One (Injective) function
A function f: X → Y is said to be a one-to-one function if the images of distinct elements of X under f are distinct. Thus, f is one to one if f(x1) = f(x2)
Property: A function f: A → B is one-to-one if f(x1) = f(x2) implies x1 = x2, i.e, an image of a distinct element of A under f mapping (function) is distinct.
Condition to be One-to-One function: Every element of the domain has a single image with a codomain after mapping.
Read More about One-to-One Functions.
Examples of One to One Functions
Som of examples of one-one functions are:
- f(x) = x (Identity function)
- k(x) = 2x + 3 (Linear Polynomial)
- g(x) = ex (Exponential function)
- h(x) = √x (Square root function, defined for x ≥ 0)
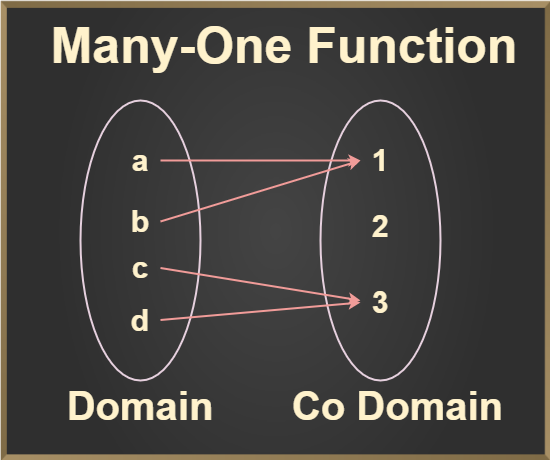
Many to One Function
If the function is not one to one function, then it should be many to one function means every element of the domain has more than one image at codomain after mapping.
- Property: One or more elements having the same image in the codomain
- Condition to be Many to One function: One or more than one element in the domain having a single image in the codomain.
Read More about Many One Functions.
Examples of Many to One Function
Some of the most common examples of many to one functions are:
- f(x) = x2 (Squared function)
- g(x) = sin(x) (Sine function)
- h(x) = cos(x) (Cosine function)
- k(x) = tan(x) (Tangent function)
- m(x) = ∣x∣ (Absolute value function)
Onto (Surjective) Function
A function f: X → Y is said to be an onto function if every element of Y is an image of some element of set X under f, i.e for every y ∈ Y there exists an element x in X such that f(x) = y.
Properties:
- The range of functions should be equal to the codomain.
- Every element of B is the image of some element of A.
Condition to be onto function: The range of function should be equal to the codomain.
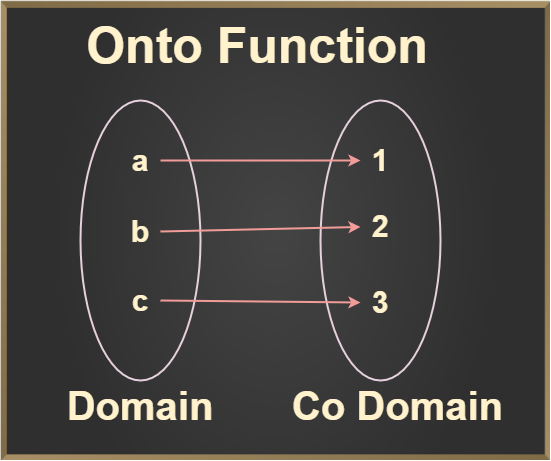
As we see in the above two images, the range is equal to the codomain means that every element of the codomain is mapped with the element of the domain, as we know that elements that are mapped in the codomain are known as the range. So these are examples of the Onto function.
Read More about Onto Functions.
Examples of Onto Functions
Some of the most common examples of onto functions are:
- f(x) = x (Identity function)
- g(x) = ex (Exponential function)
- h(x) = sin(x) (Sine function within a limited domain, e.g., h : R→[−1,1])
- k(x) = cos(x) (Cosine function within a limited domain, e.g., k : [0,π]→[−1,1])
- m(x) = x3 (Cubic function)
Into Function
A function f: X → Y is said to be an into a function if there exists at least one element or more than one element in Y, which does not have any pre-images in X, which simply means that every element of the codomain are not mapped with elements of the domain.
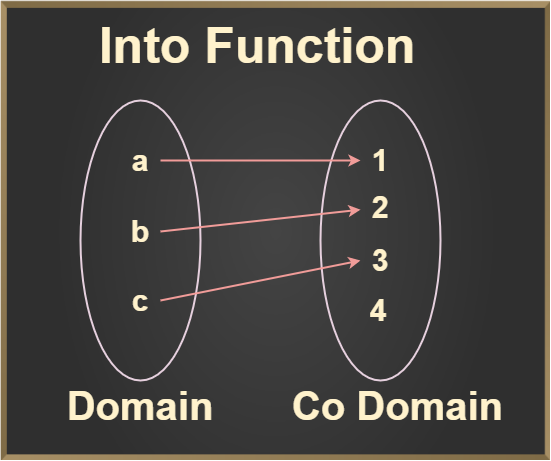
From the above image, we can clearly see that every element of the codomain is not mapped with elements of the domain means the 10th element of the codomain is left unmapped. So this type of function is known as Into function.
Properties:
- The Range of function is the proper subset of B
- The Range of functions should not equal B, where B is the codomain.
Examples of Into Functions
Some examples of into functions you can consider are:
- f(x) = sin(x) where f:R→[−1,1] is not onto because it doesn’t cover all values in the interval [−1,1][−1,1].
- g(x) = x2 where g:R→R+ (positive real numbers) is not onto because it doesn’t map to any negative real numbers.
- h(x) = ex where h:R→(0,∞) is not onto because it doesn’t map to zero.
Summary: Types of Functions
All types can be summarized in the following table:
| Function Type |
Definition |
Example |
| One-to-One (Injective) |
A function where each element of the domain maps to a unique element in the codomain. |
f(x) = 2x+3 |
| Many-to-One |
A function where multiple elements of the domain may map to the same element in the codomain. |
f(x) = x2 |
| Onto (Surjective) |
A function where every element in the codomain is mapped to by at least one element in the domain. |
f(x) = ex, f : R→(0,∞) |
| Into (Non-surjective) |
A function that does not cover the entire codomain; there are elements in the codomain that are not mapped to by any element in the domain. |
f(x) = sin(x), f:R→[−1,1] |
Read More,
Solved Examples on Types of Function
Example 1: Check whether the function f(x) = 2x + 3, is one-to-one or not if Domain = {1, 2, 1/2} and Codomain = {5, 7, 4}
Solution:
Putting 1, 2, 1/2 in place of x in f(x) = 2x + 3, we get
f(1) = 5,
f(2) = 7,
f(1/2) = 4
As, for every value of x we get a unique f(x) thus, we can conclude that our function f(x) is One to One.
Example 2: Check whether the function is one-to-one or not: f(x) = 3x – 2
Solution:
To check whether a function is one to one or not, we have to check that elements of the domain have only a single pre-image in codomain or not. For checking, we can write the function as,
f(x1) = f(x2)
3x1 – 2 = 3x2 – 2
3x1 = 3x2
x1 = x2
Since both x1 = x2 which means that elements of the domain having a single pre-image in its codomain. Hence the function f(x) = 3x – 2 is one to one function.
Example 3: Check whether the function is one-to-one or not: f(x) = x2 + 3.
Solution:
To check whether the function is One to One or not, we will follow the same procedure. Now let’s check, we can write the function as,
f(x1) = f(x2)
(x1)2 + 3 = (x2)2 + 3
(x1)2 = (x2)2
Since (x1)2 = (x2)2 is not always true.
Hence the function f(x) = x2 + 3 is not one to one function.
Example 4: If N: → N, f(x) = 2x + 1 then check whether the function is injective or not.
Solution:
In question N → N, where N belongs to Natural Number, which means that the domain and codomain of the function is a natural number. For checking whether the function is injective or not, we can write the functions as,
Let, f(x1) = f(x2)
2x1 + 1= 2x2 + 1
2x1 = 2x2
x1 = x2
Since x1 = x2, means all elements of the domain are mapped with a single element of the codomain. Hence function f(x) = 2x + 1 is Injective (One to One).
Example 5: f(x) = x2, check whether the function is Many to One or not.
Solution:
Domain = {1, -1, 2, -2}, let’s put the elements of the domain in the function
f(1) = 12 = 1
f(-1) = (-1)2 = 1
f(2) = (2)2 = 4
f(-2) = (-2)2 = 4
Thus, we can see that more than one element of the domain have similar image after mapping. So this is Many to One function.
Example 6: If f(x) = 2x + 1 is defined on R:→ R. Then check whether the following function is Onto or not
Solution:
For checking the function is Onto or not, Let’s first put the function f(x) equal to y
f(x) = y
y = 2x + 1
y – 1 = 2x
x = (y – 1) / 2
Now put the value of x in the function f(x), we get,
f((y – 1) / 2) = 2 × [(y – 1) / 2] +1
Taking LCM 2, we get
= [2(y – 1) + 2] / 2
= (2y – 2 + 2) / 2
= y
Since we get back y after putting the value of x in the function. Hence the given function f(x) = 2x + 1 is Onto function.
Example 7: If f:N → N is defined by f(x) = 3x + 1. Then prove that function f(x) is Surjective.
Solution:
To prove that the function is Surjective or not, firstly we put the function equal to y. Then find out the value of x and then put that value in the function. So let’s start solving it.
Let f(x) = y
3x + 1 = y
3x = y – 1
x = (y – 1) / 3
Now put the value of x in the function f(x), we get
f((y – 1) / 3) = {3 (y – 1) / 3} + 1
= y – 1 + 1
= y
Since we get back y after putting the value of x in the function. Hence the given function f(x) = (3x + 1) is Onto function.
Example 8: If A = R – {3} and B = R – {1}. Consider the function f: A → B defined by f(x) = (x – 2)/(x – 3), for all x ∈ A. Then show that the function f is bijective.
Solution:
To show the function is bijective we have to prove the given function both One to One and Onto.
Let’s first check for One to One:
Let x1, x2 ∈ A such that f(x1) = f(x2)
Then, (x1 – 2) / (x1 – 3) = (x2 – 2) / (x2 – 3)
(x1 – 2) ( x2 – 3) = (x2 – 2) (x1 – 3)
x1 . x2 – 3x1 – 2x1 + 6 = x1 . x2 – 3x2 -2x1 + 6
-3x1 – 2x2 = -3x2 – 2x1
-3( x1 – x2) + 2( x1 – x2) = 0
-( x1 – x2) = 0
x1 – x2 = 0
⇒ x1 = x2
Thus, f(x1) = f(x2) ⇒ x1 = x2, ∀ x1, x2 ∈ A
So, the function is a One to One
Now let us check for Onto:
Let y ∈ B = R – {1} be any arbitrary element.
Then, f(x) = y
⇒ (x – 2) / (x – 3) = y
⇒ x – 2 = xy – 3y
⇒ x – xy = 2 – 3y
⇒ x(1 – y) = 2 – 3y
⇒ x = (2 – 3y) / (1 – y) or x = (3y – 2) / (y – 1)
Now put the value of x in the function f(x)
f((3y – 2) / (y – 1)) = { (3y – 2) / (y – 1) } – 2 / { (3y – 2) / (y – 1) – 3 }
= (3y – 2 – 2y + 2) / (3y – 2 – 3y + 3)
= y
Hence f(x) is Onto function. Since we proved both One to One and Onto this implies that the function is Bijective.
Example 9: A = {1, 2, 3, 4}, B = {a, b, c, d} then the function is defined as f = {(1, a), (2, b), (3, c), (4, d)}. Check whether the function is One to One Onto or not.
Solution:
To check whether the function is One to One Onto or not. We have to check for both one by one.
Let’s check for One to One:
As we know the condition for One to One that all the elements of the domain are having a single image in the codomain. As we see in the mapping that all the elements of set A are mapped with set B and each having a single image after mapping.
So the function is One to One.
Now let’s check for Onto:
As we know the condition for the function to be Onto is that, Range = Codomain means all the elements of codomain are mapped with domain elements, in this case, codomain will equal to the domain. As we see in the mapping that the condition of the function to be Onto is satisfied.
So the function is Onto.
Since we had proved that the function is both One to One and Onto.
Hence function is One to One Onto (Bijective).
Example 10: A = {1, 2, 3, 4}, B = {a, b, c, d}. The function is defined as f = {(1, a), (2, b), (3, c), (4, c)}. Check whether the function is Many to One Into or not.
Solution:
To check the function is Many to One Into or not. We have to check for both one by one.
Let’s first check for Many to One function:
As we know the condition for Many to One function is that more than one element of domain should have more same image in codomain. From the above mapping we can see that the elements of A {3, 4 } are having same image in B { c }, so the function is Many to One.
Now let’s check for Into function:
As we know the condition for Into function is that the Range of function should be the subset of codomain and also not equal to codomain. Let’s check both the conditions are satisfied or not.
- Range of function = {a, b, c}
- Codomain of function = {a, b, c, d}
Range of function ≠ Codomain of function
As we check that the range of function is not equal to codomain of the function. Hence we can say that the function is Into function. As we prove that the function is Many to One and Into.
Hence the function is Many to One Into.
FAQs on Types of Function
What is domain and codomain of a function?
A domain of a function is defined as the set of values for which the function is defined. The function exist inside its domain. A codomain of a function is defined as the set of all possible output values f that function.
Define a function.
A function is defined as a relation between a set of values where for each input we have only one output.
Write the ways in which a function is represented.
A function is represented as y = f(x) where, x is the input value and f(x) is the output value.
How to Solve Cubic Functions?
The general form of cubic function is f(x) = ax3 + bx2 + cx +d, and if f(a) = 0, then x-a is the factor of this cubic function.
How do you prove that a Function is Onto?
In an onto function range is equal to co-domain, so any function is onto only when its range is equal to its codomain.
Suggested Quiz
1 Questions
If f:[0, ∞)→[0, ∞) and f(x) = x/(1 + x), then f is
Explanation:
Given: f(x) = x/(1 + x)
Let x, y ∈ [0, ∞) such that f(x) = f(y)
⇒ x/(1 + x) = y/(1 + y)
⇒ x + xy = y + xy
⇒ x = y
Therefore, function is one-one.
For f(x) = 1,
⇒ x/(x + 1) = 1,
⇒ x = x + 1
⇒ 0 = 1 (which is not possible)
Thus, for f(x) = 1, there is no pre image in the domain.
Quiz Completed Successfully
Your Score : 2/1
Accuracy : 0%
Login to View Explanation
1/1
1/1
< Previous
Next >
Similar Reads
CBSE Class 12 Maths Notes: Chapter Wise Notes PDF 2024
Mathematics is an important subject in CBSE Class 12th Board Exam. There is a common misunderstanding among students that Math is a complex subject. If students will plan their preparation and revision in right direction, they can score well in Mathematics. For this Purpose, We have curated the Chap
15+ min read
Chapter 1: Relations and Functions
Types of Functions
Functions are defined as the relations which give a particular output for a particular input value. A function has a domain and codomain (range). f(x) usually denotes a function where x is the input of the function. In general, a function is written as y = f(x). Table of Content What is a Function?T
14 min read
Composite functions - Relations and functions
Let f : A->B and g : B->C be two functions. Then the composition of f and g, denoted by g o f, is defined as the function g o f : A->C given by g o f (x) = g{f(x)}, ∀ x ∈ A. Clearly, dom(g o f) = dom(f). Also, g o f is defined only when range(f) is a subset of dom(g). Evaluating composite f
5 min read
Invertible Functions
As the name suggests Invertible means "inverse", and Invertible function means the inverse of the function. Invertible functions, in the most general sense, are functions that "reverse" each other. For example, if f takes a to b, then the inverse, f-1, must take b to a. Table of Content Invertible F
15+ min read
Composition of Functions
Composition of Function is the process or operation which combines two or more functions together into a single function. We define functions as the set of operations that operate on a set of values and give the desired output. Suppose f is a function say a function which draws the sketch of the fru
12 min read
Inverse Functions | Definition, Condition for Inverse and Examples
Inverse Functions are an important concept in mathematics. An inverse function basically reverses the effect of the original function. If you apply a function to a number and then apply its inverse, you get back the original number. For example, if a function turns 2 into 5, the inverse function wil
9 min read
Verifying Inverse Functions by Composition
A function can be seen as a mathematical formula or a machine that throws output when an input is given. The output is usually some processed version of the input. Function's inverses can be seen as the operations which give us the input back on giving them the output. In other words, inverse functi
5 min read
Chapter 2: Inverse Trigonometric Functions
Inverse Trigonometric Functions | Definition, Formula, Types and Examples
Inverse trigonometric functions are the inverse functions of basic trigonometric functions. In mathematics, inverse trigonometric functions are also known as arcus functions or anti-trigonometric functions. The inverse trigonometric functions are the inverse functions of basic trigonometric function
12 min read
Graphs of Inverse Trigonometric Functions - Trigonometry | Class 12 Maths
Inverse trigonometric functions are the inverse functions of the trigonometric ratios i.e. sin, cos, tan, cot, sec, cosec. These functions are widely used in fields like physics, mathematics, engineering and other research fields. There are two popular notations used for inverse trigonometric functi
7 min read
Properties of Inverse Trigonometric Functions
Inverse trigonometric functions, also known as arc functions, are used to find the angle that corresponds to a given trigonometric value. These functions are the inverses of the six main trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant. In this article, we will explore
7 min read
Inverse Trigonometric Identities
Inverse Trigonometric Identities: In mathematics, inverse trigonometric functions are also known as arcus functions or anti-trigonometric functions. The inverse trigonometric functions are the inverse functions of basic trigonometric functions, i.e., sine, cosine, tangent, cosecant, secant, and cota
10 min read
Chapter 3: Matrices
Types of Matrices
A matrix is a rectangular array of numbers arranged in rows and columns. Each element in the matrix is identified by its position, which is denoted as "aij", where "i" is the row number and "j" is the column number of the element. A matrix is typically represented as [A]m×n, where m is the number
14 min read
Matrix Operations
Matrix Operations are basic calculations performed on matrices to solve problems or manipulate their structure. Common operations include: Addition: Add two matrices of the same size.Subtraction: Subtract two matrices of the same size.Scalar Multiplication: Multiply each element of a matrix by a con
7 min read
Matrix Addition
Matrix Addition is widely used in various fields such as data analysis, computer graphics, image processing, cryptography, operations research, machine learning, artificial intelligence, and more. As the title suggests, this article explores matrix addition, which is one of the fundamental operation
12 min read
Matrix Multiplication
Matrix multiplication is a fundamental operation in mathematics that involves multiplying two or more matrices according to specific rules. Understanding how to multiply matrices is crucial for solving various mathematical problems. Matrix multiplication combines two matrices to produce a new matrix
13 min read
Transpose of a Matrix
A matrix is a rectangular arrangement of numbers (or elements) in rows and columns. It is often used in mathematics to represent data, solve systems of equations, or perform transformations. A matrix is written as: [Tex]A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9\e
11 min read
Symmetric and Skew Symmetric Matrices
Symmetric and Skew Symmetric Matrices are the types of square matrices based on the relation between a matrix and its transpose. These matrices are one of the most used matrices out of all the matrices out there. Symmetric matrices have use cases in optimization, physics, and statistics, whereas ske
10 min read
Elementary Operations on Matrices
Elementary Operations on Matrices are the operations performed on the rows and columns of the matrix that do not change the value of the matrix. A matrix is a way of representing numbers in the form of an array, i.e. the numbers are arranged in the form of rows and columns. In a matrix, the rows and
9 min read
Inverse of a Matrix by Elementary Operations - Matrices | Class 12 Maths
The Gaussian Elimination method is also known as the row reduction method and it is an algorithm that is used to solve a system of linear equations. It is usually understood as a sequence of operations performed on the corresponding matrix of coefficients. Inverse of a MatrixThe inverse of a matrix
8 min read
Invertible Matrix
Invertible matrices are defined as the matrix whose inverse exists. We define a matrix as the arrangement of data in rows and columns, if any matrix has m rows and n columns then the order of the matrix is m × n where m and n represent the number of rows and columns respectively. We define invertib
13 min read
Chapter 5: Continuity and Differentiability
Continuity and Discontinuity in Calculus
Continuity and Discontinuity: Continuity and discontinuity are fundamental concepts in calculus and mathematical analysis, describing the behavior of functions. A function is continuous at a point if you can draw the graph of the function at that point without lifting your pen from the paper. Contin
7 min read
Differentiability of a Function | Class 12 Maths
Continuity or continuous which means, "a function is continuous at its domain if its graph is a curve without breaks or jumps". A function is continuous at a point in its domain if its graph does not have breaks or jumps in the immediate neighborhood of the point. Continuity at a Point: A function f
11 min read
Derivatives of Inverse Functions
In mathematics, a function(e.g. f), is said to be an inverse of another(e.g. g), if given the output of g returns the input value given to f. Additionally, this must hold true for every element in the domain co-domain(range) of g. E.g. assuming x and y are constants if g(x) = y and f(y) = x then the
12 min read
Derivatives of Implicit Functions - Continuity and Differentiability | Class 12 Maths
Implicit functions are functions where a specific variable cannot be expressed as a function of the other variable. A function that depends on more than one variable. Implicit Differentiation helps us compute the derivative of y with respect to x without solving the given equation for y, this can be
6 min read
Derivatives of Composite Functions
Derivatives are an essential part of calculus. They help us in calculating the rate of change, maxima, and minima for the functions. Derivatives by definition are given by using limits, which is called the first form of the derivative. We already know how to calculate the derivatives for standard fu
6 min read
Derivatives of Inverse Trigonometric Functions
Derivatives of Inverse Trigonometric Functions: Every mathematical function, from the simplest to the most complex, has an inverse. In mathematics, the inverse usually means the opposite. In addition, the inverse is subtraction. For multiplication, it's division. In the same way for trigonometric fu
14 min read
Derivative of Exponential Functions
Derivative of Exponential Function stands for differentiating functions expressed in the form of exponents. We know that exponential functions exist in two forms, ax where a is a real number r and is greater than 0 and the other form is ex where e is Euler's Number and the value of e is 2.718 . . .
8 min read
Logarithmic Differentiation - Continuity and Differentiability
The word continuity means something which is continuous in nature. The flow of water is continuous, time in real life is continuous, and many more instances show the continuity in real life. In mathematics, the Continuous function is the one which when drawn on a graph does not show any breaks and i
5 min read
Proofs for the derivatives of eˣ and ln(x) - Advanced differentiation
In this article, we are going to cover the proofs of the derivative of the functions ln(x) and ex. Before proceeding there are two things that we need to revise: The first principle of derivative Finding the derivative of a function by computing this limit is known as differentiation from first prin
3 min read
Rolle's Theorem and Lagrange's Mean Value Theorem
Rolle's Theorem and Lagrange's Mean Value Theorem: Mean Value Theorems (MVT) are the basic theorems used in mathematics. They are used to solve various types of problems in Mathematics. Mean Value Theorem is also called Lagrenges's Mean Value Theorem. Rolle’s Theorem is a subcase of the mean value t
11 min read
Derivative of Functions in Parametric Forms
Parametric Differentiation refers to the differentiation of a function in which the dependent and independent variables are equated to a third variable. Derivatives of the functions express the rate of change in the functions. We know how to calculate the derivatives for standard functions. Chain ru
7 min read
Second Order Derivatives: Rules , Formula and Examples (Class 12 Maths)
The Second Order Derivative is defined as the derivative of the first derivative of the given function. The first-order derivative at a given point gives us the information about the slope of the tangent at that point or the instantaneous rate of change of a function at that point. Second-Order Deri
10 min read
Mean Value Theorem
The Mean Value Theorem states that for a curve passing through two given points there exists at least one point on the curve where the tangent is parallel to the secant passing through the two given points. Mean Value Theorem is abbreviated as MVT. This theorem was first proposed by an Indian Mathem
13 min read
Algebra of Continuous Functions - Continuity and Differentiability | Class 12 Maths
Algebra of Continuous Functions deals with the utilization of continuous functions in equations involving the varied binary operations you've got studied so. We'll also mention a composition rule that may not be familiar to you but is extremely important for future applications. Since the continuity
7 min read
Chapter 6: Applications of Derivatives
Critical Points
As the complexity of the functions increase, we see more and more complex behavior from their graphs, and it becomes harder to graph. There have lots of peaks and valleys in their graphs. It becomes essential to find out the position of these valleys and peaks, the peaks are called maxima and the va
8 min read
Derivatives as Rate of Change
Derivatives are a mathematical tool used to analyze how quantities change. We can calculate derivatives for various, quotient, and chain rulesfunctions, including trigonometric, exponential, polynomial, and implicit functions. There are two main methods for calculating derivatives: using limits or a
7 min read
Increasing and Decreasing Functions
If you're studying calculus, then you're probably familiar with the concepts of increasing and decreasing functions. These terms refer to the behaviour of a function as its input values change. An increasing function is one where the output (or value) grows as the input (or domain) increases. Conver
12 min read
Increasing and Decreasing Intervals
Increasing and decreasing intervals are the intervals of real numbers in which real-valued functions are increasing and decreasing respectively. Derivatives are a way of measuring the rate of change of a variable. When it comes to functions and calculus, derivatives give us a lot of information abou
11 min read
Tangents and Normals
Tangent and Normals are the lines that are used to define various properties of the curves. We define tangent as the line which touches the circle only at one point and normal is the line that is perpendicular to the tangent at the point of tangency. Any tangent of the curve passing through the poin
13 min read
Equation of Tangents and Normals
Derivatives are used to find rate of change of a function with respect to variables. To find rate of change of function with respect to a variable differentiating it with respect to that variable is required. Rate of change of function y = f(x) with respect to x is defined by dy/dx or f'(x). For exa
6 min read
Relative Minima and Maxima
Relative maxima and minima are the points defined in any function such that at these points the value of the function is either maximum or minimum in their neighborhood. Relative maxima and minima depend on their neighborhood point and are calculated accordingly. We find the relative maxima and mini
8 min read
Absolute Minima and Maxima
Absolute Maxima and Minima are the maximum and minimum values of the function defined on a fixed interval. A function in general can have high values or low values as we move along the function. The maximum value of the function in any interval is called the maxima and the minimum value of the funct
12 min read
Concave Function
Graphs of the functions give us a lot of information about the nature of the function, the trends, and the critical points like maxima and minima of the function. Derivatives allow us to mathematically analyze these functions and their sign can give us information about the maximum and minimum of th
10 min read
Inflection Point
Inflection Point describes a point where the curvature of a curve changes direction. It represents the transition from a concave to a convex shape or vice versa. Let's learn about Inflection Points in detail, including Concavity of Function and solved examples. Table of Content Inflection Point Defi
9 min read
Curve Sketching
Curve Sketching as its name suggests helps us sketch the approximate graph of any given function which can further help us visualize the shape and behavior of a function graphically. Curve sketching isn't any sure-shot algorithm that after application spits out the graph of any desired function but
15 min read
Approximations - Application of Derivatives
An approximation is similar but not exactly equal to something else. Approximation occurs when an exact numerical number is unknown or difficult to obtain. In Mathematics, we use differentiation to find the approximate values of certain quantities. Let f be a given function and let y = f(x). Let ∆x
4 min read
Higher Order Derivatives
Higher order derivatives refer to the derivatives of a function that are obtained by repeatedly differentiating the original function. The first derivative of a function, f′(x), represents the rate of change or slope of the function at a point.The second derivative, f′′(x), is the derivative of the
6 min read
Chapter 7: Integrals
Integrals
Integrals: An integral in mathematics is a continuous analog of a sum that is used to determine areas, volumes, and their generalizations. Performing integration is the process of computing an integral and is one of the two basic concepts of calculus. Integral in Calculus is the branch of Mathematic
11 min read
Integration by Substitution Method
Integration by substitution or u-substitution is a highly used method of finding the integration of a complex function by reducing it to a simpler function and then finding its integration. Suppose we have to find the integration of f(x) where the direct integration of f(x) is not possible. So we su
8 min read
Integration by Partial Fractions
Integration by Partial Fractions is one of the methods of integration, which is used to find the integral of the rational functions. In Partial Fraction decomposition, an improper-looking rational function is decomposed into the sum of various proper rational functions. If f(x) and g(x) are polynomi
8 min read
Integration by Parts
Integration by Parts or Partial Integration, is a technique used in calculus to evaluate the integral of a product of two functions. The formula for partial integration is given by: ∫ u dv = uv - ∫ v du Where u and v are differentiable functions of x. This formula allows us to simplify the integral
10 min read
Integration of Trigonometric Functions
Integration is the process of summing up small values of a function in the region of limits. It is just the opposite to differentiation. Integration is also known as anti-derivative. We have explained the Integration of Trigonometric Functions in this article below. Below is an example of the Integr
9 min read
Functions Defined by Integrals
While thinking about functions, we always imagine that a function is a mathematical machine that gives us an output for any input we give. It is usually thought of in terms of mathematical expressions like squares, exponential and trigonometric function, etc. It is also possible to define the functi
5 min read
Definite Integral | Definition, Formula & How to Calculate
A definite integral is an integral that calculates a fixed value for the area under a curve between two specified limits. The resulting value represents the sum of all infinitesimal quantities within these boundaries. i.e. if we integrate any function within a fixed interval it is called a Definite
9 min read
Computing Definite Integrals
Integrals are a very important part of the calculus. They allow us to calculate the anti-derivatives, that is given a function's derivative, integrals give the function as output. Other important applications of integrals include calculating the area under the curve, the volume enclosed by a surface
5 min read
Fundamental Theorem of Calculus | Part 1, Part 2
Fundamental Theorem of Calculus is the basic theorem that is widely used for defining a relation between integrating a function of differentiating a function. The fundamental theorem of calculus is widely useful for solving various differential and integral problems and making the solution easy for
11 min read
Finding Derivative with Fundamental Theorem of Calculus
Integrals are the reverse process of differentiation. They are also called anti-derivatives and are used to find the areas and volumes of the arbitrary shapes for which there are no formulas available to us. Indefinite integrals simply calculate the anti-derivative of the function, while the definit
5 min read
Evaluating Definite Integrals
Integration, as the name suggests is used to integrate something. In mathematics, integration is the method used to integrate functions. The other word for integration can be summation as it is used, to sum up, the entire function or in a graphical way, used to find the area under the curve function
9 min read
Properties of Definite Integrals
Properties of Definite Integrals: An integral that has a limit is known as a definite integral. It has an upper limit and a lower limit. It is represented as [Tex]\int_{a}^{b}[/Tex]f(x) = F(b) − F(a) There are many properties regarding definite integral. We will discuss each property one by one with
8 min read
Definite Integrals of Piecewise Functions
Imagine a graph with a function drawn on it, it can be a straight line or a curve or anything as long as it is a function. Now, this is just one function on the graph, can 2 functions simultaneously occur on the graph? Imagine two functions simultaneously occurring on the graph, say, a straight line
8 min read
Improper Integrals
Improper integrals are definite integrals where one or both of the boundaries are at infinity or where the Integrand has a vertical asymptote in the interval of integration. Computing the area up to infinity seems like an intractable problem, but through some clever manipulation, such problems can b
5 min read
Riemann Sums
Riemann Sum is a certain kind of approximation of an integral by a finite sum. A Riemann sum is the sum of rectangles or trapezoids that approximate vertical slices of the area in question. German mathematician Bernhard Riemann developed the concept of Riemann Sums. In this article, we will look int
7 min read
Riemann Sums in Summation Notation
Riemann sums allow us to calculate the area under the curve for any arbitrary function. These formulations help us define the definite integral. The basic idea behind these sums is to divide the area that is supposed to be calculated into small rectangles and calculate the sum of their areas. These
8 min read
Trapezoidal Rule
The Trapezoidal Rule is a fundamental method in numerical integration used to approximate the value of a definite integral of the form b∫a f(x) dx. It estimates the area under the curve y = f(x) by dividing the interval [a, b] into smaller subintervals and approximating the region under the curve as
13 min read
Definite Integral as the Limit of a Riemann Sum
Definite integrals are an important part of calculus. They are used to calculate the areas, volumes, etc of arbitrary shapes for which formulas are not defined. Analytically they are just indefinite integrals with limits on top of them, but graphically they represent the area under the curve. The li
7 min read
Antiderivative: Integration as Inverse Process of Differentiation
An antiderivative is a function that reverses the process of differentiation. It is also known as the indefinite integral. If F(x) is the antiderivative of f(x), it means that: d/dx[F(x)] = f(x) In other words, F(x) is a function whose derivative is f(x). Antiderivatives include a family of function
6 min read
Indefinite Integrals
Integrals are also known as anti-derivatives as integration is the inverse process of differentiation. Instead of differentiating a function, we are given the derivative of a function and are required to calculate the function from the derivative. This process is called integration or anti-different
6 min read
Particular Solutions to Differential Equations
Indefinite integrals are the reverse of the differentiation process. Given a function f(x) and it's derivative f'(x), they help us in calculating the function f(x) from f'(x). These are used almost everywhere in calculus and are thus called the backbone of the field of calculus. Geometrically speaki
7 min read
Integration by U-substitution
Finding integrals is basically a reverse differentiation process. That is why integrals are also called anti-derivatives. Often the functions are straightforward and standard functions that can be integrated easily. It is easier to solve the combination of these functions using the properties of ind
8 min read
Reverse Chain Rule
Integrals are an important part of the theory of calculus. They are very useful in calculating the areas and volumes for arbitrarily complex functions, which otherwise are very hard to compute and are often bad approximations of the area or the volume enclosed by the function. Integrals are the reve
6 min read
Partial Fraction Expansion
If f(x) is a function that is required to be integrated, f(x) is called the Integrand, and the integration of the function without any limits or boundaries is known as the Indefinite Integration. Indefinite integration has its own formulae to make the process of integration easier. However, sometime
9 min read
Trigonometric Substitution: Method, Formula and Solved Examples
Trigonometric substitution is a process in which the substitution of a trigonometric function into another expression takes place. It is used to evaluate integrals or it is a method for finding antiderivatives of functions that contain square roots of quadratic expressions or rational powers of the
7 min read
Chapter 8: Applications of Integrals
Area under Simple Curves
We know how to calculate the areas of some standard curves like rectangles, squares, trapezium, etc. There are formulas for areas of each of these figures, but in real life, these figures are not always perfect. Sometimes it may happen that we have a figure that looks like a square but is not actual
6 min read
Area Between Two Curves: Formula, Definition and Examples
Area Between Two Curves in Calculus is one of the applications of Integration. It helps us calculate the area bounded between two or more curves using the integration. As we know Integration in calculus is defined as the continuous summation of very small units. The topic "Area Between Two Curves" h
7 min read
Area between Polar Curves
Coordinate systems allow the mathematical formulation of the position and behavior of a body in space. These systems are used almost everywhere in real life. Usually, the rectangular Cartesian coordinate system is seen, but there is another type of coordinate system which is useful for certain kinds
6 min read
Area as Definite Integral
Integrals are an integral part of calculus. They represent summation, for functions which are not as straightforward as standard functions, integrals help us to calculate the sum and their areas and give us the flexibility to work with any type of function we want to work with. The areas for the sta
8 min read
Chapter 9: Differential Equations
Differential Equations
A differential equation is a mathematical equation that relates a function with its derivatives. Differential Equations come into play in a variety of applications such as Physics, Chemistry, Biology, Economics, etc. Differential equations allow us to predict the future behavior of systems by captur
13 min read
Particular Solutions to Differential Equations
Indefinite integrals are the reverse of the differentiation process. Given a function f(x) and it's derivative f'(x), they help us in calculating the function f(x) from f'(x). These are used almost everywhere in calculus and are thus called the backbone of the field of calculus. Geometrically speaki
7 min read
Homogeneous Differential Equations
Homogeneous Differential Equations are differential equations with homogenous functions. They are equations containing a differentiation operator, a function, and a set of variables. The general form of the homogeneous differential equation is f(x, y).dy + g(x, y).dx = 0, where f(x, y) and h(x, y) i
9 min read
Separable Differential Equations
Separable differential equations are a special type of ordinary differential equation (ODE) that can be solved by separating the variables and integrating each side separately. Any differential equation that can be written in form of y' = f(x).g(y), is called a separable differential equation. Basic
8 min read
Exact Equations and Integrating Factors
Differential Equations are used to describe a lot of physical phenomena. They help us to observe something happening in real life and put it in a mathematical form. At this level, we are mostly concerned with linear and first-order differential equations. A differential equation in “y” is linear if
10 min read
Implicit Differentiation
Implicit Differentiation is the process of differentiation in which we differentiate the implicit function without converting it into an explicit function. For example, we need to find the slope of a circle with an origin at 0 and a radius r. Its equation is given as x2 + y2 = r2. Now, to find the s
6 min read
Implicit differentiation - Advanced Examples
In the previous article, we have discussed the introduction part and some basic examples of Implicit differentiation. So in this article, we will discuss some advanced examples of implicit differentiation. Table of Content Implicit DifferentiationMethod to solveImplicit differentiation Formula Solve
5 min read
Advanced Differentiation
Derivatives are used to measure the rate of change of any quantity. This process is called differentiation. It can be considered as a building block of the theory of calculus. Geometrically speaking, the derivative of any function at a particular point gives the slope of the tangent at that point of
8 min read
Disguised Derivatives - Advanced differentiation | Class 12 Maths
The dictionary meaning of “disguise” is “unrecognizable”. Disguised derivative means “unrecognized derivative”. In this type of problem, the definition of derivative is hidden in the form of a limit. At a glance, the problem seems to be solvable using limit properties but it is much easier to solve
6 min read
Derivative of Inverse Trigonometric Functions
Derivative of Inverse Trigonometric Function refers to the rate of change in Inverse Trigonometric Functions. We know that the derivative of a function is the rate of change in a function with respect to the independent variable. Before learning this, one should know the formulas of differentiation
11 min read
Logarithmic Differentiation
Method of finding a function's derivative by first taking the logarithm and then differentiating is called logarithmic differentiation. This method is specially used when the function is type y = f(x)g(x). In this type of problem where y is a composite function, we first need to take a logarithm, ma
8 min read
Chapter 10: Vector Algebra
Vector Algebra
Vectors algebra is the branch of algebra that involves operations on vectors. Vectors are quantities that have both magnitude and direction so normal operations are not performed on the vectors. We can add, subtract, and multiply vector quantities using special vector algebra rules. Vectors can be e
14 min read
Dot and Cross Products on Vectors
A quantity that is characterized not only by magnitude but also by its direction, is called a vector. Velocity, force, acceleration, momentum, etc. are vectors. Vectors can be multiplied in two ways: Scalar product or Dot productVector Product or Cross productTable of Content Scalar Product/Dot Pr
9 min read
How to Find the Angle Between Two Vectors?
Vector quantities are the physical quantities that have both magnitude and direction and the angle between two vectors can be easily found if the dot product or the cross product of the two vectors is given. In this article, we will learn how to find the angle between two vectors, its formula, relat
6 min read
Section Formula - Vector Algebra
The section formula in vector algebra is a useful formula for finding a point that divides a line segment into a certain ratio. This concept is particularly important in physics and engineering for tasks such as finding center of mass, centroids, and other applications where a point must be located
12 min read
Chapter 11: Three-dimensional Geometry
Direction Cosines and Direction Ratios
Usually, for three-dimensional geometry, we rely on the three-dimensional Cartesian plane. Vectors can also be used to describe the lines and the angles they make with the axis. How should we describe a line passing through the origin making an angle with different axes? We define them using cosine
8 min read
Equation of a Line | Definition, Different Forms and Examples
The equation of a line in a plane is given as y = mx + C where x and y are the coordinates of the plane, m is the slope of the line and C is the intercept. However, the construction of a line is not limited to a plane only. We know that a line is a path between two points. These two points can be lo
15+ min read
Angles Between two Lines in 3D Space | Solved Examples
A line in mathematics and geometry is a fundamental concept representing a straight, one-dimensional figure that extends infinitely in both directions. Lines are characterized by having no thickness and being perfectly straight. Here are some important aspects and definitions related to lines: Key C
8 min read
Shortest Distance Between Two Lines in 3D Space | Class 12 Maths
The shortest distance between two lines in three-dimensional space is the length of the perpendicular segment drawn from a point on one line to the other line. This distance can be found using vector calculus or analytical geometry techniques, such as finding the vector equation of each line and cal
7 min read
Points, Lines and Planes
Points, Lines, and Planes are basic terms used in Geometry that have a specific meaning and are used to define the basis of geometry. We define a point as a location in 3-D or 2-D space that is represented using the coordinates. We define a line as a geometrical figure that is extended in both direc
14 min read
Chapter 12: Linear Programming
Chapter 13: Probability
Conditional Probability and Independence - Probability | Class 12 Maths
Conditional probability and independence are important concepts in probability theory. Conditional probability deals with the likelihood of an event occurring given that another event has already occurred. Independence, on the other hand, refers to situations where the occurrence of one event does n
11 min read
Multiplication Theorem
Probability refers to the extent of the occurrence of events. When an event occurs like throwing a ball, picking a card from the deck, etc ., then there must be some probability associated with that event. In terms of mathematics, probability refers to the ratio of wanted outcomes to the total numbe
8 min read
Dependent and Independent Events
Dependent and Independent Events are the types of events that occur in probability. Suppose we have two events say Event A and Event B then if Event A and Event B are dependent events then the occurrence of one event is dependent on the occurrence of other events if they are independent events then
8 min read
Bayes' Theorem
Bayes' Theorem is used to determine the conditional probability of an event. It is used to find the probability of an event, based on prior knowledge of conditions that might be related to that event. Bayes' Theorem and Conditional ProbabilityBayes theorem (also known as the Bayes Rule or Bayes Law)
11 min read
Probability Distribution - Function, Formula, Table
A probability distribution describes how the probabilities of different outcomes are assigned to the possible values of a random variable. It provides a way of modeling the likelihood of each outcome in a random experiment. While a frequency distribution shows how often outcomes occur in a sample or
15+ min read
Binomial Distribution in Probability
Binomial Distribution is a probability distribution used to model the number of successes in a fixed number of independent trials, where each trial has only two possible outcomes: success or failure. This distribution is useful for calculating the probability of a specific number of successes in sce
15 min read
Binomial Mean and Standard Deviation - Probability | Class 12 Maths
Binomial distribution is the probability distribution of no. of Bernoulli trials i.e. if a Bernoulli trial is performed n times the probability of its success is given by binomial distribution. Keep in mind that each trial is independent of another trial with only two possible outcomes satisfying th
7 min read
Bernoulli Trials and Binomial Distribution
Bernoulli Trials and Binomial Distribution are the fundamental topics in the study of probability and probability distributions. Bernoulli's Trials are those trials in probability where only two possible outcomes are Success and Failure or True and False. Due to this fact of two possible outcomes, i
13 min read
Discrete Random Variable
Discrete Random Variables are an essential concept in probability theory and statistics. Discrete Random Variables play a crucial role in modelling real-world phenomena, from the number of customers who visit a store each day to the number of defective items in a production line. Understanding discr
15 min read
Expected Value
Expected Value: Random variables are the functions that assign a probability to some outcomes in the sample space. They are very useful in the analysis of real-life random experiments which become complex. These variables take some outcomes from a sample space as input and assign some real numbers t
15+ min read
NCERT Solution for Class 12 Maths 2024-25 : Chapter Wise PDF Download
NCERT Solution for Class 12 Maths: Maths is one of the most scoring subject in Class 12th board exam 2024-25. The syllabus of CBSE Maths exam is based on latest NCERT Math syllabus. So, GeeksforGeeks has curated the NCERT Class 12 Maths Solution for you to prepare. Students can also download the NCE
7 min read
RD Sharma Class 12 Solutions for Maths
RD Sharma Solutions for class 12 provide solutions to a wide range of questions with a varying difficulty level. With the help of numerous sums and examples, it helps the student to understand and clear the chapter thoroughly. Solving the given questions inside each chapter of RD Sharma will allow t
12 min read