A Study Regarding Solution of a Knowledge Model Based on the Containing-Type Error Matrix Equation ()
1. Introduction
The truth is always expected; however, error should be avoided and eliminated firstly in order to seek truth. On the one hand, it should be known why and how the error arises with the aim of avoiding and eliminating errors; on the other hand, it should be known how to eradicate it when error appears. Moreover, within a faultless system, proposition and decision can also be naturally transferred into being defective in normal conditions, because of the passage of time, changes in natural conditions, or development of science. So, errors are required to be eliminated continuously.
Chinese scholar Professor Guo Kaizhong has found the error-eliminating theory since the 1980s, and has taken the study of error to a new level.
The error-eliminating theory is an emerging subject, which is used to study error elimination [1]. The theory of error-eliminating defines the objective system, in which one error factor at least is included to characterize and eliminate errors. Error setting could be termed as  . As mentioned in the book “Theory of Error Sets” [2], all unary or multiple error sets have been defined in error matrix. In the book “Error Logic” [3], every element
. As mentioned in the book “Theory of Error Sets” [2], all unary or multiple error sets have been defined in error matrix. In the book “Error Logic” [3], every element  is expressed as
is expressed as

from the standpoint of logic theory, where U is discussing domain;  is the objects of u;
is the objects of u;  is the space under consideration, and
is the space under consideration, and  is used to define the dimensions in the space;
is used to define the dimensions in the space;  is the characteristic of the described objects;
is the characteristic of the described objects;  is the value of
is the value of  is error function;
is error function;  are decision rules. As shown in the above function, object
are decision rules. As shown in the above function, object  and rule
and rule  are set as independent variables. In addition to this, Guo Kaizhong, Liu Shiyong and Li Min [5-7] have studied Logical relationship among various types of error logical words.
are set as independent variables. In addition to this, Guo Kaizhong, Liu Shiyong and Li Min [5-7] have studied Logical relationship among various types of error logical words.
Error matrix based on error logic is a useful method of modeling for scenes. X, A and B could be structured as an error matrix equation for three error matrix, such as XA = B. XA = B is just a concrete form of error matrix equation . By means of solving the error matrix equation, matrix X of error logic transformation can be obtained, which can be used in reasoning regarding the question. X allows us to find a method, in which bad status “A” changes into good status “B”. Guo Kaizhong and Min Xilin [8-10] have studied the solution of equation XA = B, in which a containing-type error matrix, such as XA Ê B, was found to be more suited for analyzing the actual question. In this paper, it is attempted to solve the containing-type error matrix in order to seek new ways of error-elimination.
. By means of solving the error matrix equation, matrix X of error logic transformation can be obtained, which can be used in reasoning regarding the question. X allows us to find a method, in which bad status “A” changes into good status “B”. Guo Kaizhong and Min Xilin [8-10] have studied the solution of equation XA = B, in which a containing-type error matrix, such as XA Ê B, was found to be more suited for analyzing the actual question. In this paper, it is attempted to solve the containing-type error matrix in order to seek new ways of error-elimination.
2. Error Matrix Equation
2.1. Equational-Type Error Matrix Equation
In the previous research, all of the error matrix equations have been classified into two types (see Table 1). There are five kinds of equations in each type. Meanwhile, there are three constraints on the solution of the equation: The first is an objective condition, named “kg”; the second is a stipulation that has been confirmed, named “rw”; the third is the restriction of requirement, named “xq”.
In common situations, these three restrictions above can be shown by certain sets. The factors in the matrix and the solving of the matrix equations are also measured in a certain set. Therefore, we can use the intersection method of solving sets which includes the matrix equation and ignores these three restrictions in solving the process.
2.2. Containing-Type Error Matrix Equation
In order to analyze practical issues, we propose a containing-type error matrix equation (see Table 2).
3. Solving a Containing-Type Error Matrix Equation
In the following, let us now consider how to solve the second type of equation (1): XA Ê B.



Table 1. Classification of equational-type error matrix equation.

Table 2. Classification of containing-type error matrix equation.

Definition 3.1. Suppose

One element of the matrix
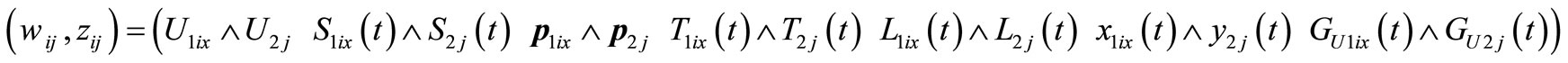
Therefore

According to the definition of matrix equivalent: .
.
So

That is

i.e., according to the corresponding factors in these two matrixes, the equations below are obtained:















If both sides of the equation are all sets, operator “∧”means the operation of intersection. If both sides of the equation are values, operator “∧”means the operation of minimization.
In fact, the equation sets above are not irrelevant. After calculation, the factors of matrix can compose a complete proposition. This can be defined as

“hi, i = 1, 2, ∙∙∙, 6” means a complete matrix element composition can be composed after calculating. The methods of composing are decided according to the specific situation. One way is the multiplication of m × 7- order error matrix, from which is composed a new error set or error logical proposition by using each parameter from calculation to be the corresponding parameter.
Theorem 1. A necessary and sufficient condition of solving error matrix equation  is that equation
is that equation , i = (1,2, ∙∙∙, m2) has a solution.
, i = (1,2, ∙∙∙, m2) has a solution.
Proof: if XA´=B has a solution, according to the equivalent equations and
and , i = (1,2, ∙∙∙, m2), the equation
, i = (1,2, ∙∙∙, m2), the equation , i = (1,2, ∙∙∙, m2) should have a solution first; Vice versa, if
, i = (1,2, ∙∙∙, m2) should have a solution first; Vice versa, if , i = (1,2, ∙∙∙, m2) has a solution, we also can know
, i = (1,2, ∙∙∙, m2) has a solution, we also can know  has a solution by the same principle.
has a solution by the same principle.
So, we can discuss the solution of equation , the same as when solving
, the same as when solving  , i = (1,2, ∙∙∙, m2).
, i = (1,2, ∙∙∙, m2).
With respect to ,
,

i.e.

There are equations:























Theorem 2. Necessary and sufficient condition of solving error matrix equation  is:
is:























Proof of necessity: If one of above conditions is not satisfied, for example, condition  is not satisfied, then in equation
is not satisfied, then in equation  no matter what the value of
no matter what the value of  is,
is,  cannot be calculated.
cannot be calculated.
Proof of sufficiency: The condition  is satisfied in error matrix equation
is satisfied in error matrix equation , so the element of Xi, which corresponds to element A, take union of set. i.e.,
, so the element of Xi, which corresponds to element A, take union of set. i.e.,







Q.ed.
Then discussing the whole solution of equations  and
and .
.
After solving  of
of , by taking the intersection of X, kg, rw and xq, we can acquire
, by taking the intersection of X, kg, rw and xq, we can acquire .
.
4. Application Example of Error Matrix Equation
For example: suppose ,
,




Each element included in a11, a12, a21, a22 is A set type. For instance, an element of discussing domain U201 has several elements under it. So U201 can be expressed as . Thus, we could express all the elements as follows:
. Thus, we could express all the elements as follows:







n = 11;







n = 9;








n = 10;







n = 15;
Suppose ,
,


and ,
,




The representation of all the elements of b11, b12, b21, b22 is the same as a11, a12, a21, a22. So they can be expressed as follows:







k = 7;







k = 8;







k = 2;







k = 3.
The three constraints of kg, rw and xq are described below.








n = 4, j = 5.








n = 10.








n = 8.
By Theorem 2, the solution of  is:
is:







n = 11.
Combining the three constrains of kg, rw, xq to U10X mentioned above, the solution satisfied X ∩ kg ∩ rw ∩ xq is:







n = 4.
In the same way, we can acquire:







n = 8.
Combining the three constrains of kg, rw, xq to U11X mentioned above, the solution satisfying X ∩ kg ∩ rw ∩ xq is:







n = 4.
5. Conclusions
In order for a decision to be correct, we need to know the rule of how errors generate or convert. Each object in real world can be indicated as (u,x). Every element (u,x) is expressed as

from the standpoint of logic theory. An error matrix can be constructed when the seven parameters mentioned above in (u,x) are used as matrix columns. And three error matrixes X, A, B can create an error matrix equation . Matrix A is express current status and matrix B is expectant status, X is what we want to achieve. X allows us to find a method, in which bad status “A” changes into good status “B”.
. Matrix A is express current status and matrix B is expectant status, X is what we want to achieve. X allows us to find a method, in which bad status “A” changes into good status “B”.
Based on the error matrix equation, which is a kind of mathematical tool to be used to describe error itself and the transformation rules of errors, this paper proposes a new kind of error matrix equation named “containingtype error matrix equation”. The method of solving, existence and form of solution for this type of equation have been presented in this paper. Our research provides a new method of decision making.