1. Introduction
In the recent years, one-dimensional complex Hamiltonians 
have generated lot of interest for the understanding of several newly discovered phenomena in various science-streams [1,2], but such studies in mathematical terms have not been reached to the desired extent. Several attempts have been made to obtain the solutions of Schrödinger equation (SE) for different anharmonic potentials in real domain. However, the study of complex octic potential has become of considerable interest due to the peculiar nature of the eigenvalue spectrum. Further, besides some general studies of complex Hamiltonians in nonlinear domain [1,3], efforts have been made to study both classical and quantum aspects [4-7] of a system. At the classical context, 
becomes the function of two complex variables and the analyticity property of 
leads to a class of integrable systems in the associated twodimensional real systems 
and
, where, 
act as new Hamiltonian and 
is a second integral of motion. The possible connection between 
and 
is sought in terms of anti-Bäcklund transformation [5]. In the quantum context, as 
which implies 
and
, the analyticity of
is translated into complex potential
. While a complex Hamiltonian is no longer hermitian and ordinarily does not guarantee for real eigenvalues, however, in 
-symmetric version [8-10], the system is found to exhibit real and bounded eigenvalue spectrum, The reality of the spectrum is a consequence of combined action of the parity and time reversal invariance of Hamiltonian [6]. Recently, following the work of C. M. Bender et al. [8,9], one-dimensional Hamiltonian systems have been studied rigorously through combined parity and time reversal operators. The parity operator 
and time reversal operator 
defined by the action of position and momentum operators are
;
The combined action of parity-time operator is
(1)
where,
. Here, the operators 
and 
are real, the commutator 
is invariant under operators 
and
. It is interesting to note that commutation relation still remain invariant even if 
and 
becomes complex, provided that above transformation hold. There are various ways of complexifying a given Hamiltonian [11], but here we use the scheme given by Xavier and de Aguir [12,13], used to develop an algorithm for the computation of semiclassical coherent state propagator to transform potentials in extended complex phase space approach (ECPSA). The real and imaginary parts of 
and 
are introduced as
if, we define 
, then 
and 
can be defined as
(2)
The presence of variables 
in the above transformations may be regarded as some sort of co-ordinate momentum interactions of a dynamical system. Note that, in this complexifying scheme, the degrees of freedom of the underlying system just become double. The 
-symmetric condition for the above transormation becomes 
Though complex potentials are in practice for a long time, such as in optical model of nucleus, delocalization transition in condensed matter system—such as vortex flux line dippening in type-II superconductors, yet the quantum mechanics of complex potentials has not been studied to a desired level. It is since last few years that the study of complex potentials has become important enough for better theoretical understanding of the detailed properties of some newly discovered phenomena in physics and chemistry, like the phenomena pertaining to resonance scattering in atomic, molecular, and nuclear physics and to some chemical reactions [14-17]. The complex Hamiltonian is used in several other theoretical context likestudies of complex trajectories with regard to the calculation of semiclassical coherent-state propagator in the path integral method have attracted particular interest in laser physics [12,13]. The 
-symmetric non-hermitian Hamiltonians have many applications in various fields of physics-like superconductivity, population biology, quantum cosmology, condensed matter physics, quantum field theory etc.
Transformations similar to Equation (2) have also been used in the study of nonlinear evolution equations in context of amplitude-modulated nonlinear Langmuir waves in plasma [4]. Recently, in some studies, solutions of the Schrödinger wave equation have been reported using the extended complex phase space approach (ECPSA) [11,18,19]. With this motivation and to expand the domain of applications, we investigate the quasiexact solution of the analogous Schrödinger equation (ASE) for a coupled complex octic potential and its variant in one dimension.
The paper is organized as follows: in Section 2, we are devoted with the mathematical formulation of the ECPSA for computing the ground state and excited state eigenvalue spectra of some one-dimensional complex systems. Under the same mathematical prescription, ground state solutions are presented in Section 3 and excited state solutions are described in Section 4. Finally, concluding remarks are presented in Section 5.
2. General Results
For a complex Hamiltonian system 
in one dimension, the ASE (for
) is given by
(3)
where
(4)
Here, Equation (3) departs from the conventional and mathematical setting of the standard Schrödinger equation [20], so Equation (3) is termed as analogous Schrö- dinger equation (ASE) for a non-hermitian operator
. The transformation condition (2) implies that
(5)
Note that, the momentum operator 
of the conventional quantum mechanics under the transformation (2) reduces to 
This relation yields
,
. Also, the complex co-ordinate transformation (2) preserves the fundamental commutation relations, 
, which can be easily verified with the help of Equations (2) and (5). To express the ASE (3) into a pair of coupled partial differential equation, the complex forms of 
and E are written as
(6a)
(6b)
(6c)
where, subscripts “r” and “I” denote the real and imaginary parts of the corresponding quantities and other subscripts to these quantities separated by comma will denote the partial derivatives of the quantity concerned. Thus, after inserting Equations (2), (4) and (6a)-(6c) in Equation (3) and separating the real and imaginary parts in the final expression, one gets the following pair of partial differential equations
(7a)
(7b)
The analyticity property of the wavefunction
, in terms of Cauchy-Riemann conditions, implies
(8)
Under the analyticity condition (8), Equations (7a) and (7b), reduces to
(9a)
(9b)
The ansatz for the wavefunction 
is taken as [19]
(10)
where, 
and 
are the polynomial functions of the complex variable
, which can be expressed as
(11a)
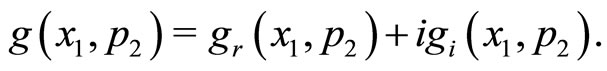(11b)
After utilizing Equations (6b), (9b), (11a) and (11b) in Equation (10), the real and imaginary parts of the wavefunction are expressed as
(12a)
(12b)
In view of the analyticity condition (8), 
and 
satisfies the relations
(13)
Therefore, with the help of Equations (12a) and (12b), the Equations (9a) and (9b) yield
(14a)
(14b)
It is to be noted that for given functional forms of 
and
, the rationalization of Equations (14a) and (14b) yield the real and imaginary components of the energy eigenvalue spectrum for the excited state of a system. On the other hand, if 
is chosen as constant, then Equations (14a) and (14b) reduces to ground state solutions as
(15a)
(15b)
With a suitable ansatz for
, satisfying the analyticity condition (19), the rationalization of Equations (15a) and (15b), provides ground state solutions of the ASE for a given complex potential.
3. Ground State Solutions
Here, we look for the ground state solutions of onedimensional complex octic potential and its variant as:
3.1. Generalized Octic Potential
Consider a generalized octic potential of the form
(16)
where, the coupling parameters 
are complex i.e.
and
, 
are constants.
Under the 
-symmetric condition (1), the potential (24) reduces to
(17)
By implying the transformation (2) on the potential (17), the real and imaginary parts of the potential turn out to be
(18)
(19)
The polynomial forms of 
and
, in conformity with (13) are written as
(20a)
(20b)
where, 
and 
are real. Now, inserting the above forms of 
and 
in Equations (15a) and (15b), the rationalization of the resultant expression yields the following set of non-repeating equations
(21a)
(21b)
(21c)
(21d)
(21e)
(21f)
(21g)
(21h)
(21i)
(21j)
Here, Equations (21c)-(21j) except (21e) give rise to the constraining relations among the potential parameters. However, the Equations (21e), (21h) and (21j) can be immediately solved for four arbitrary constants i.e.
, 
, 
and
. Whereas Equations (21d)-(21j) can be solved for some negative values of 
say 
in the potential (17). The results obtained are
(22)
(23)
where,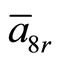 
is real positive. The constraining relations obtained from Equations (21c), (21d), (21f) and (21g) are
The presence of these constraining relations, makes the problem quasi solvable. Such relations can be helpful in definition and approximate sub domain in complex parametric space in which a given complex potential provides real spectra. As from Equation (21b), imaginary part of the energy eigenvalue is zero, while the real part of the energy eigenvalue obtained from Equation (21a) turns out to be
(24)
The corresponding eigenfunction becomes
(25)
3.2. Variant of Octic Potential
Here, we consider one-dimensional octic potential (16) with the inverse harmonic term as
(26)
where, the potential parameters 
and 
are complex constants. By implying the 
-symmetric condition (2) on the potential (26), one gets
(27)
Implying the transformation (2), the real and imaginary parts of the potential (26) are written as
(28a)
(28b)
where, 
and 
are same as given by Equations (18) and (19). The functional form of 
and 
complying with the analyticity condition (13) are written as
(29a)
(29b)
As before, using these forms of 
and 
in Equations (15a) and (15b), the rationalization of the resultant expression yield a set of equations in addition to Equations (21f)-(21j) as
(30a)
(30b)
(30c)
(30d)
(30e)
(30f)
The pair of Equations (30e) and (30f) immediately lead us to
(31a)
The additional constraining relations given by Equations (30c) and (30d) are
Under the similar prescription as adopted in previous case, the imaginary component of the energy eigenvalue vanishes, whereas the real component of the energy is
(32)
The ground state eigenfunction for the potential (44) turn out to be
(33)
4. Excited State Solutions
Here, we elaborate viability of the prescription laid down in Sections 2 and 3 to compute eigenvalue and corresponding eigenfunction for the first excited state. The functional form of 
for the first excited state is taken as
(34)
Then, under the transformation (2), the above equation reduces to
(35)
where, 
and 
are considered as real constants. In order to compute the corresponding energy eigenvalue and eigenfunction for the first excited state of potential (16), we use the same functional forms of 
and 
as mentioned in Equations (20a) and (20b). After inserting the Equations (20a), (20b) and (35) in Equations (14a) and (14b), then equating the coefficients of 
and their various products to zero, one gets the following set of non-repeating equations in addition to Equations (21f)- (21j)
(36a)
(36b)
(36c)
(36d)
(36e)
Inserting Equations (21h)-(21j) in Equation (36e), we have
(37)
The other potential parameters are same as described in earlier section, whereas the constraining relations obtained from Equations (36c) and (36d) are
Using the various ansatz parameters in Equation (36a), the real component of energy eigenvalue is written as
(38)
whereas the eigenfunction is given by
(39)
Variant of Octic Potential
Again to compute energy eigenvalue and corresponding eigenfunction for the first excited state of potential (26), we use the same functional forms of 
and 
as mentioned in Equations (29a) and (29b). Then implying Equations (20a), (20b) and (35) in Equations (14a) and (14b), the rationalization of the final expression yields the following set of non-repeating equations in addition to Equations (21f)-(21j)
(40a)
(40b)
(40c)
(40d)
(40e)
(40f)
The Equations (40e) and (40f) lead us to
(41a)
(41b)
The other ansatz parameters are same as for ground state solutions. However, the additional constraining relations given by Equations (40c) and (40d) are
Under the similar prescription as in previous case, the energy eigenvalue and eigenfunction are given by
(42)
(43)
5. Concluding Remarks
In the present work, we have investigated quasi-exact 
-symmetric solutions of the ASE for one-dimensional octic potential and its variants using ECPSA. Besides complexity of the phase space produced by transformation (2), complexity of the potential parameters is also taken into account and ground state as well as excited states solutions are worked out. It is also emphasized that solutions of the ASE in the above said cases are obtained only in the presence of certain constraining relations among potential parameters, such constraining relations give rise to bound states of a system. It is found that imaginary part of the energy eigenvalue always vanishes for the solvable case of ASE, as long as all potential parameters are real. However, for 
- symmetric potentials, energy eigenvalues are found real, even if concerned potentials possess complex parameters. The interesting aspect of this method is an account of complex coupling coefficients of potential in addition to complex phase space. Thus present method suggests another degree of freedom to obtain the real spectra for non-hermitian operator.
6. Acknowledgements
The author expresses his gratitude to Prof. S. C. Mishra and Dr. Fakir Chand, Department of Physics, Kurukshetra University, Kurukshetra (India), for their valuable suggestions regarding the manuscript.