An Application of the Maximum Theorem in Multi-Criteria Optimization, Properties of Pareto-Retract Mappings, and the Structure of Pareto Sets ()
1. Introduction
The Berge Maximum Theorem, shortly the Maximum Theorem, has become one of the most useful and powerful theorems in optimization theory, mathematical economics and game theory. The original variant of the Maximum Theorem is as follows:
Theorem 1 [1] [2, Theorem 9.14]. Let  and
and ,
,  be a continuous function, and
be a continuous function, and  be a compact-valued and continuous multifunction. Then, the function
be a compact-valued and continuous multifunction. Then, the function  defined by
defined by  is continuous on X, and the multifunction
is continuous on X, and the multifunction  defined by
defined by  is compact-valued and upper semi-continuous on X.
is compact-valued and upper semi-continuous on X.
The Maximum Theorem is often used in a special situation when the multifunction D is convex-valued and the function u is quasi-concave or concave in its second variable in addition to the hypotheses of Theorem 1.
Now, we give a presentation of the classical variant of the Maximum Theorem.
Theorem 2 [2, Theorem 9.17 and Corollary 9.20]. Let  and
and ,
,  be a continuous function, and
be a continuous function, and  be a compact-valued and continuous multifunction. Define m and S as in Theorem 1.
be a compact-valued and continuous multifunction. Define m and S as in Theorem 1.
(a) Then m is a continuous function on X, and S is a compact-valued and upper semi-continuous multifunction on X.
(b) If  is quasi-concave in y for each
is quasi-concave in y for each , and D is convex-valued, then S is convex-valued.
, and D is convex-valued, then S is convex-valued.
(c) If  is strictly quasi-concave in y for each
is strictly quasi-concave in y for each , and D is convex-valued, then S is a continuous function on X.
, and D is convex-valued, then S is a continuous function on X.
(d) If u is concave on , and D has a convex graph, then m is a concave function on X and S is a convex-valued multifunction on X.
, and D has a convex graph, then m is a concave function on X and S is a convex-valued multifunction on X.
(e) If u is strictly concave on , and D has a convex graph, then m is a strictly concave and continuous function on X, and S is a continuous function on X.
, and D has a convex graph, then m is a strictly concave and continuous function on X, and S is a continuous function on X.
Remark 1. It is important to note the following two facts [2, Example 9.15 and 9.16]:
(1) S is only upper semi-continuous, and not necessarily also lower semi-continuous.
(2) The continuity of u on  cannot be replaced with one of separate continuity, i.e., that
cannot be replaced with one of separate continuity, i.e., that  is continuous on X for each fixed
is continuous on X for each fixed  and that
and that  is continuous on Y for each fixed
is continuous on Y for each fixed .
.
Let us consider Theorem 2. It is possible to have  for all
for all . Obviously, the following theorem is true.
. Obviously, the following theorem is true.
Theorem 3. Let  and
and ,
,  be a continuous function, and
be a continuous function, and  be a compact-valued and continuous multifunction. Define m and S as in Theorem 1. If
be a compact-valued and continuous multifunction. Define m and S as in Theorem 1. If  for all
for all , then m and S are two continuous function on X.
, then m and S are two continuous function on X.
2. Basic Concepts and Definitions
It is easy to show that Theorems 1, 2 and 3 imply the following two theorems.
Theorem 4. Let ,
,  be a continuous function, and
be a continuous function, and  be a continuous multifunction. Then, the function
be a continuous multifunction. Then, the function  defined by
defined by  is continuous on X, and the multifunction
is continuous on X, and the multifunction  defined by
defined by  is upper semi-continuous on X.
is upper semi-continuous on X.
Theorem 5. Let ,
,  be a continuous function, and
be a continuous function, and  be a continuous multifunction. Define m and S as in Theorem 4. If
be a continuous multifunction. Define m and S as in Theorem 4. If  for all
for all , then m and S are two continuous function on X.
, then m and S are two continuous function on X.
Now we will apply these two theorems to multi-criteria optimization.
The general form of the multi-criteria unconstrained optimization problem is to find a variable  ,
,  , so as to maximize
, so as to maximize  subject to
subject to , where the feasible domain X is nonempty and compact,
, where the feasible domain X is nonempty and compact,  is the index set,
is the index set,  ,
,  is a given objective continuous function for all
is a given objective continuous function for all .
.
Now we will introduce several solution concepts for our multi-criteria optimization problem.
Definition 1.
(a) A point  is called an ideal Pareto-optimal solution if and only if
is called an ideal Pareto-optimal solution if and only if  for all
for all  and all
and all . The set of the ideal Pareto-optimal solutions of X is denoted by
. The set of the ideal Pareto-optimal solutions of X is denoted by  and is called an ideal Pareto-optimal set.
and is called an ideal Pareto-optimal set.
(b) A point  is called a Pareto-optimal solution if and only if there does not exist a point
is called a Pareto-optimal solution if and only if there does not exist a point  such that
such that  for all
for all  and
and  for some
for some . The set of the Pareto-optimal solutions of X is denoted by
. The set of the Pareto-optimal solutions of X is denoted by  and is called a Pareto-optimal set. Its image
and is called a Pareto-optimal set. Its image  is called a Pareto-front set.
is called a Pareto-front set.
(c) A point  is called a strictly Pareto-optimal solution if and only if there does not exist a point
is called a strictly Pareto-optimal solution if and only if there does not exist a point  such that
such that  for all
for all  and
and . The set of the strictly Pareto-optimal solutions of X is denoted by
. The set of the strictly Pareto-optimal solutions of X is denoted by  and is called a strictly Pareto-optimal set.
and is called a strictly Pareto-optimal set.
The above definition qualifies Pareto-optimal solutions in the global sense.
In literature, the term Pareto-optimal is frequently used synonymously with efficient, non-inferior and non-dominated.
In our optimization problem, it can be shown that:  is nonempty, but
is nonempty, but  and
and  may be empty;
may be empty;  and
and  , see also [3-5].
, see also [3-5].
Remark 2. It is well-known that  when
when  is nonempty [6].
is nonempty [6].
Usually, a Pareto-optimal solution is not necessarily uniquely determined, but there are several Pareto-optimal solutions.
For a better understanding of this paper, we recall some useful notations and definitions.
To be precise, we introduce the following notations: for every two vectors ,
,  means
means  for all
for all ,
,  means
means  for all
for all  (weakly component-wise order),
(weakly component-wise order),  means
means  for all
for all  (strictly component-wise order), and
(strictly component-wise order), and  means
means  for all
for all  and
and  for some
for some  (component-wise order).
(component-wise order).
Remark 3. Let X and Y be two topological spaces. A homotopy between two continuous functions  is defined to be a continuous function
is defined to be a continuous function  such that
such that  and
and  for all
for all . Note that we can consider the homotopy H as a continuously deformation of f to g [7].
. Note that we can consider the homotopy H as a continuously deformation of f to g [7].
Definition 2.
(a) The set  is a retract of X if and only if there exists a continuous function
is a retract of X if and only if there exists a continuous function  such that
such that  for all
for all . The function r is called a retraction of X to Y.
. The function r is called a retraction of X to Y.
(b) The set  is a deformation retract of X if and only if there exist a retraction
is a deformation retract of X if and only if there exist a retraction  and a homotopy
and a homotopy  such that
such that  and
and  for all
for all .
.
Remark 4. From a more formal viewpoint, a retraction is a function  such that
such that  for all
for all , since this equation says exactly that r is the identity on its image. Retractions are the topological analogs of projection operators in other parts of mathematics. It is true that every deformation retract is a retract, but in generally the converse does not hold [7].
, since this equation says exactly that r is the identity on its image. Retractions are the topological analogs of projection operators in other parts of mathematics. It is true that every deformation retract is a retract, but in generally the converse does not hold [7].
Applications of retractions in multi-criteria optimization have been discussed by several authors [3,8-12].
We are now ready to define:
1) A multifunction  by
by  for all
for all .
.
2) A multifunction  by
by  for all
for all .
.
3) A function  by
by  for all
for all .
.
Note that, for each ,
,  is equal to the intersection of all the upper contour sets and
is equal to the intersection of all the upper contour sets and  is equal to the intersection of all the level sets. Clearly,
is equal to the intersection of all the level sets. Clearly,  for all
for all .
.
Remark 5. From Definition 1 it is easy directly verify that for :
:
(1)  is equivalent to
is equivalent to  (or equivalently
(or equivalently ).
).
(2)  is equivalent to
is equivalent to .
.
Choose  and consider an optimization problem with a single objective function as follows: 1) Maximize
and consider an optimization problem with a single objective function as follows: 1) Maximize  subject to
subject to  or 2) maximize
or 2) maximize  subject to
subject to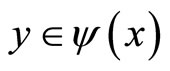 . By letting x vary over all of X we can identify different Pareto-optimal solutions. This optimization technique will allow us to find the whole Paretooptimal set and analyze its structure.
. By letting x vary over all of X we can identify different Pareto-optimal solutions. This optimization technique will allow us to find the whole Paretooptimal set and analyze its structure.
Remark 6. It is known that  for all
for all  [6].
[6].
The above remark allows us to present a new definition.
Definition 3.
(a) A multifunction  is a called Pareto-retract (Pareto-retract point-to-set mapping) if and only if
is a called Pareto-retract (Pareto-retract point-to-set mapping) if and only if  for all
for all .
.
(b) A function  is called a Paretoretract (Pareto-retract point-to-point mapping) if and only if
is called a Paretoretract (Pareto-retract point-to-point mapping) if and only if  for all
for all .
.
Thus we introduce the concept of the Pareto-retract mappings. Here the fundamental idea is based on the observation that for any  which is not Paretooptimal there exists at least one other
which is not Paretooptimal there exists at least one other  such that
such that  for all
for all  and strictly inequality holds at least once.
and strictly inequality holds at least once.
According to Remark 6, one can see that there exists a Pareto-retract multifunction, but an open problem is its continuity (lower or upper semi-continuous).
3. Assumptions and Theorems in the General Case
In this section, we will discuss the role of the following assumptions that affect the characteristics of a Paretoretract mapping (Pareto-retract multifunction and Paretoretract function) if the feasible domain X is compact:
Assumption 1.  is lower semi-continuous on X.
is lower semi-continuous on X.
Assumption 2a.  for all
for all .
.
Assumption 2b. There exists  such that
such that  for all
for all .
.
Note that if Assumption 2a holds, then there exists a Pareto-retract function, see also Remark 6. Again, an open problem is its continuity.
These assumptions allow us to present our theorems of this section.
Theorem 6.  is upper semi-continuous on X.
is upper semi-continuous on X.
Proof. We will prove that if  and
and  are a pair of sequences such that
are a pair of sequences such that  and
and  for all
for all , then there exists a convergent subsequence of
, then there exists a convergent subsequence of  whose limit belongs to
whose limit belongs to .
.
The assumption  for all
for all  implies
implies  for all
for all . From the condition
. From the condition  it follows that there exists a convergent subsequence
it follows that there exists a convergent subsequence  such that
such that  . Therefore, there exists a convergent subsequence
. Therefore, there exists a convergent subsequence  such that
such that  and
and . Thus, we find that
. Thus, we find that  for all
for all . Taking the limit as
. Taking the limit as  we obtain
we obtain , i.e.
, i.e. . This means that
. This means that  is upper semi-continuous on X.
is upper semi-continuous on X.
The theorem is proven.
We are now ready to prove the following basic theorem.
Theorem 7. If Assumption 1 holds, then:
(a)  is continuous on X.
is continuous on X.
(b) There exists an upper semi-continuous Pareto-retract multifunction.
(c)  and
and  are compact.
are compact.
Proof.
(a) Assumption 1 and Theorem 6 imply that  is continuous on X.
is continuous on X.
(b) According Remark 6 we are in a position to construct a multifunction  such that
such that  for all
for all . It is easy to show that
. It is easy to show that 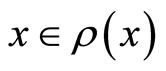 for
for . This means that
. This means that .
.
The function s is continuous and the multifunction  is compact-valued and continuous. Now applying Theorem 4, we conclude that
is compact-valued and continuous. Now applying Theorem 4, we conclude that  is an upper semi-continuous multifunction on the compact domain X.
is an upper semi-continuous multifunction on the compact domain X.
(c) We recall that X is compact; therefore, part (b) implies that  is compact too. Trivially,
is compact too. Trivially,  is compact.
is compact.
The theorem is proven.
Remark 7. Let Assumption 1 be satisfied. Remark 1 shows that the multifunction  is not necessarily lower semi-continuous.
is not necessarily lower semi-continuous.
Theorem 8. If Assumption 2a or 2b holds, then .
.
Proof. It is well-known that .
.
Let  and assume that
and assume that . From the fact that
. From the fact that  it follows that there exists
it follows that there exists  such that
such that  for all
for all 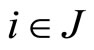 and
and . Hence,
. Hence, .
.
There are two cases:
(1) If Assumption 2a holds, then there exists a unique  such that
such that  for all
for all . But we get that
. But we get that  and
and . This means that
. This means that ,
,  and
and  for all
for all . As a result we obtain
. As a result we obtain  for all
for all  and
and  for some
for some . This leads to a contradiction.
. This leads to a contradiction.
(2) If Assumption 2b holds, then there exists a unique  such that
such that  for all
for all . But we know that
. But we know that  for all
for all  and
and . This means that
. This means that ,
,  for all
for all  and
and . This leads to a contradiction too.
. This leads to a contradiction too.
Finally, we obtain .
.
The theorem is proven.
Remark 8. While studying the proof of Theorem 8, one can see that if  and
and , then
, then .
.
Theorem 9. If Assumptions 1 and 2a (or 1 and 2b) hold, then:
(a) There exists a continuous Pareto-retract function.
(b)  is homeomorphic to
is homeomorphic to .
.
Proof. (a) First, let Assumptions 1 and 2a be satisfied. In this case, we construct a function  such that
such that  for all
for all . From Theorems 5, 7 and 8, and Remark 6 it follows that r is a continuous Pareto-retract function.
. From Theorems 5, 7 and 8, and Remark 6 it follows that r is a continuous Pareto-retract function.
For the second part of this proof, let Assumptions 1 and 2b be satisfied. Now we construct a function  such that
such that  for all
for all . From Theorems 5, 7 and 8, and Remark 8 it follows that r is a continuous Pareto-retract function.
. From Theorems 5, 7 and 8, and Remark 8 it follows that r is a continuous Pareto-retract function.
(b) Recalling that the function  is continuous; therefore, a restriction
is continuous; therefore, a restriction  of f is continuous too. From Remark 5 and Theorem 8 we have that the function h is bijective. Consider the inverse function
of f is continuous too. From Remark 5 and Theorem 8 we have that the function h is bijective. Consider the inverse function  of h. We proved in Theorem 7 that
of h. We proved in Theorem 7 that  is compact; therefore,
is compact; therefore,  is continuous too [13]. As a result we conclude that the function h is homeomorphism.
is continuous too [13]. As a result we conclude that the function h is homeomorphism.
The theorem is proven.
Remark 9. From Theorem 9 we can easily check the following:
(1) For each ,
,  is nonempty compact and
is nonempty compact and .
.
(2) If  and
and , then
, then  .
.
(3) .
.
(4) By Assumption 2a, for each  we have
we have  and
and  for all
for all  .
.
(5) By Assumption 2b, for each  we have
we have  and
and  for all
for all  .
.
4. Structure of Pareto Sets
The structure of Pareto sets is very important, from an algorithmic point of view.
Let  be the Euclidean metric in
be the Euclidean metric in  and
and  be the topology induced by
be the topology induced by . In a topological space
. In a topological space , for
, for  we now recall some general topological definitions.
we now recall some general topological definitions.
Definition 4. A property is called a topological property if and only if an arbitrary topological space X has this property, then Y has this property too, where Y is homeomorphic to X.
Definition 5.
(a) The set Y is connected if and only if it is not the union of a pair of nonempty sets of , which are disjoint.
, which are disjoint.
(b) The set Y is path-wise connected if and only if for every  there exists a continuous function
there exists a continuous function  such that
such that  and
and . The function p is called a path.
. The function p is called a path.
(c) The set Y is simply connected if and only if it is path-wise connected and every path between two points can be continuously deformed into every other.
(d) The set Y is contractible (contractible to a point) if and only if there exists a point  such that
such that  is a deformation retract of Y.
is a deformation retract of Y.
Remark 10. Recalling that the following statements are true:
(1) Convexity implies contractibility, contractibility implies simply connectedness, simply connectedness implies path-wise connectedness, and path-wise connectedness implies connectedness. However, in general the converse does not hold.
(2) Contractibility, simply connectedness, path-wise connectedness and connectedness are topological properties of sets.
(3) Compactness, path-wise connectedness and connectedness of sets are preserved under a continuous function.
(4) Compactness, connectedness, path-wise connectedness, simply connectedness and contractibility of sets are preserved a under retraction.
(5) The image of a simply connected set under a continuous function need not to be simply connected.
(6) The image of a convex set under a retraction need not to be convex.
Remark 11. We now focus our attention to contractibility of sets. Let . Remark 10 has shown that if Y is a retract of X and X is contractible, then Y is contractible too. The converse does not hold in generally. But for every deformation retract the following statement is true: “If Y is a deformation retract of X, then Y is contractible if and only if X is contractible.”
. Remark 10 has shown that if Y is a retract of X and X is contractible, then Y is contractible too. The converse does not hold in generally. But for every deformation retract the following statement is true: “If Y is a deformation retract of X, then Y is contractible if and only if X is contractible.”
Definition 6.
(a) The topological space Y is said to have the fixed point property if and only if every continuous function 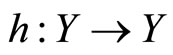 from this set into itself has a fixed point, i.e. there is a point
from this set into itself has a fixed point, i.e. there is a point  such that
such that .
.
(b) The topological space Y is said to have the Kakutani fixed point property if and only if every upper semi-continuous multifunction  from this set into itself has a fixed point, i.e. there is a point
from this set into itself has a fixed point, i.e. there is a point  such that
such that .
.
(1) Remark 12. We will use the following statements for each compact set:
Convexity implies the fixed point properties (fixed point property and Kakutani fixed point property).
(2) The fixed point properties of sets are topological properties.
(3) The fixed point properties of sets are preserved under retraction.
(4) A set having the fixed point property is equivalent to this set having the Kakutani fixed point property.
Now we focus our attention on the compactness, connectedness, contractibility and fixed point properties of the Pareto sets. Compactness of these sets is studied in [3,8,12,14-16]. Connectedness is considered in [3,6,8, 16-24]. Contractibility of Pareto sets is discussed in [9, 10,12,25]. Fixed point properties have been addressed in [10,12,26].
Corollary 1. If Assumptions 1 and 2a (or 1 and 2b) hold, then:
(a) If X is convex, then  and
and  are contractible and have the fixed point properties.
are contractible and have the fixed point properties.
(b) If X is contractible, then  and
and  are contractible.
are contractible.
(c) If X is simply connected, then  and
and  are simply connected.
are simply connected.
(d) If X is path-wise connected, then  and
and  are path-wise connected.
are path-wise connected.
(e) If X is connected, then  and
and  are connected.
are connected.
(f) If X has the fixed point properties, then  and
and  have the fixed point properties.
have the fixed point properties.
Proof. Directly, from Theorem 9, Remarks 10 and 12 imply the proof.
5. Convex Case
We often use the Maximum Theorem under convexity as a mathematical tool in convex optimization. Here we will present two special variants of this theorem and their applications to convex multi-criteria optimization.
In this section, we are going to study our optimization problem when the functions  are concave and a function
are concave and a function  of
of  is strictly quasi-concave on the compact and convex domain X.
is strictly quasi-concave on the compact and convex domain X.
Concavities of the objective functions play a central role in optimization theory, for more information see [27] and [28]. We will use the definitions of quasi-concave and concave functions in the usual sense.
Definition 7. A real function g on a convex subset  is called to be:
is called to be:
(a) Quasi-concave on X if and only if for any  and
and , then
, then  .
.
(b) Strictly quasi-concave on X if and only if for any ,
,  and
and , then
, then  .
.
(c) Concave on X if and only if for any  and
and , then
, then .
.
Now, from Theorems 2 and 4 we get the first special variant of the Maximum Theorem under convexity.
Theorem 10. Let ,
,  be a continuous function, and
be a continuous function, and  be a continuous multifunction. Define m and S as in Theorem 4. If u is quasiconcave on X and D is convex-valued, then S is a convex-valued and upper semi-continuous multifunction on X.
be a continuous multifunction. Define m and S as in Theorem 4. If u is quasiconcave on X and D is convex-valued, then S is a convex-valued and upper semi-continuous multifunction on X.
Remark 13. If  are all quasi-concave and one of them is strictly quasi-concave, then
are all quasi-concave and one of them is strictly quasi-concave, then  [3,6].
[3,6].
We are ready to prove the first theorem in this section.
Theorem 11. Let  be all concave on the compact and convex domain X. Then:
be all concave on the compact and convex domain X. Then:
(a)  is convex-valued and continuous on X. In particular, Assumption 1 holds.
is convex-valued and continuous on X. In particular, Assumption 1 holds.
(b) There exists an upper semi-continuous Pareto-retract multifunction.
(c)  and
and 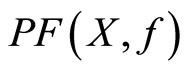 are compact.
are compact.
(d)  is convex when
is convex when .
.
(e)  for all
for all  .
.
(f) There exists a continuous function  such that
such that . In particular,
. In particular,  is path-wise connected.
is path-wise connected.
Proof. (a) Define a multifunction  such that
such that  for all
for all . It is easy to show that the multifunction
. It is easy to show that the multifunction  is convex-valued.
is convex-valued.
We will prove continuity of  on X using a two-step procedure.
on X using a two-step procedure.
Step 1. We will prove that if  and
and  are a pair of sequences such that
are a pair of sequences such that  and
and  for all
for all , then there exists a convergent subsequence of
, then there exists a convergent subsequence of  whose limit belongs to
whose limit belongs to .
.
The assumption  for all
for all  implies
implies  for all
for all . From the condition
. From the condition  it follows that there exists a convergent subsequence
it follows that there exists a convergent subsequence  such that
such that . Therefore, there exists a convergent subsequence
. Therefore, there exists a convergent subsequence  such that
such that  and
and  . Thus, we find that
. Thus, we find that  for all
for all . Taking the limit as
. Taking the limit as  we obtain
we obtain  . As a result we have
. As a result we have . In other words,
. In other words,  is upper semi-continuous on X.
is upper semi-continuous on X.
Step 2. We will prove that if  is a sequence convergent to
is a sequence convergent to  and
and , then there exists a sequence
, then there exists a sequence  such that
such that  for all
for all  and
and .
.
There are two cases:
(1) Suppose that .
.
We get that , i.e.
, i.e. . In this case let
. In this case let .
.
(2) Suppose that .
.
In this case, we will consider two possibilities:
(2.1) Suppose that .
.
From  implies
implies . Without loss of generally we can study the case when
. Without loss of generally we can study the case when  . As a result we obtain
. As a result we obtain  and let
and let .
.
(2.2) Suppose that .
.
From the fact that  is continuous and concave on the compact and convex domain X, we deduce that
is continuous and concave on the compact and convex domain X, we deduce that  is nonempty, convex and compact. Denote the distance between
is nonempty, convex and compact. Denote the distance between  and
and  by
by . Clearly,
. Clearly,  and there exists a unique
and there exists a unique  such that
such that . Consider a linear segment
. Consider a linear segment  and a restriction
and a restriction  of
of . From the definition of b it follows that: 1) If
. From the definition of b it follows that: 1) If  and
and , then
, then , 2) if
, 2) if  and
and , then
, then  for all
for all , i.e.
, i.e.  implies
implies . It is easy to show that b is bijective and continuous on
. It is easy to show that b is bijective and continuous on ; therefore, there exists a unique
; therefore, there exists a unique  such that
such that  and
and  is continuous. We obtain:
is continuous. We obtain: ,
,  ,
,  ,
,  ,
, .
.
As a result we get a sequence  such that
such that  for all
for all  and
and . This means that
. This means that  is lower semi-continuous on X.
is lower semi-continuous on X.
In summary,  is continuous on X.
is continuous on X.
Now, define a multifunction  such that
such that  for all
for all . By analogy, we prove that
. By analogy, we prove that  is convex-valued and continuous on X.
is convex-valued and continuous on X.
This procedure is repeated until all objective functions have been considered. At the end, define a multifunction  such that
such that  for all
for all . Similarly, we prove that
. Similarly, we prove that  is convex-valued and continuous on X.
is convex-valued and continuous on X.
Observe that . Hence,
. Hence,  is continuous on X and Assumption 1 holds.
is continuous on X and Assumption 1 holds.
(b) The proof follows directly from Theorems 7(b) and 11(a).
(c) This is immediate from Theorems 7(c) and 11(a).
(d) If  is nonempty, then
is nonempty, then  . In fact
. In fact  is nonempty and convex, we deduce that
is nonempty and convex, we deduce that  is convex.
is convex.
(e) It is obvious that  for all
for all .
.
We will prove that if , then
, then .
.
There are two possibilities:
(1) Suppose that .
.
The statement is trivially true.
(2) Suppose that .
.
Let ,
,  ,
,  and
and . In fact,
. In fact,  is convex, it follows that
is convex, it follows that  and s (z) = s (y1) = s (y2). But for each
and s (z) = s (y1) = s (y2). But for each  there is
there is . By using this result we derive that
. By using this result we derive that . Since
. Since 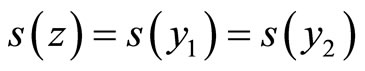 implies
implies . This means that
. This means that  for all
for all  and all
and all , i.e.
, i.e.  for all
for all . Thus, we get
. Thus, we get  for all
for all , i.e.
, i.e. .
.
Finally, according to this result and Remarks 5 and 6 we conclude that  for all
for all .
.
(f) Consider the multifunction  from Theorem 7(b). Theorem 11(e) allows us to define a function
from Theorem 7(b). Theorem 11(e) allows us to define a function  by
by . The function b is continuous on X because ρ is upper semicontinuous on X and f is continuous on
. The function b is continuous on X because ρ is upper semicontinuous on X and f is continuous on . Clearly,
. Clearly,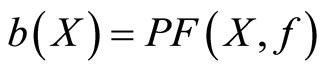 .
.
So, we get the continuous function b and we know that X is path-wise connected; therefore,  is pathwise connected too.
is pathwise connected too.
The theorem is proven.
Note that convexity plays an essential role in pathwise connectedness of the Pareto-front set.
We give the second special variant of the Maximum Theorem under convexity. It follows immediately from Theorems 2, 4 and 5.
Theorem 12. Let ,
,  be a continuous function, and
be a continuous function, and  be a continuous multifunction. Define m and S as in Theorem 4. If u is strictly quasi-concave on X and D is convex-valued, then S is a continuous function on X.
be a continuous multifunction. Define m and S as in Theorem 4. If u is strictly quasi-concave on X and D is convex-valued, then S is a continuous function on X.
Continuing with this analysis we have the following theorem.
Theorem 13. Let  be all concave on the convex domain X and
be all concave on the convex domain X and  be strictly quasi-concave on X. Then:
be strictly quasi-concave on X. Then:
(a) Assumptions 1, 2a and 2b hold.
(b) There exists a continuous Pareto-retract function.
(c)  and
and  are contractible and have the fixed point properties
are contractible and have the fixed point properties
(d) .
.
(e)  is infinite and uncountable when
is infinite and uncountable when .
.
(f)  when
when .
.
Proof. (a) Since Theorem 11(a) implies that Assumption 1 holds.
Let us fix an arbitrary point . It is obvious that
. It is obvious that . Let us assume that
. Let us assume that  . Hence, there exist
. Hence, there exist  such that
such that . According to Theorem 11(e) we derive
. According to Theorem 11(e) we derive . But
. But  is strictly quasi-concave; therefore,
is strictly quasi-concave; therefore,  . This leads to a contradiction; therefore,
. This leads to a contradiction; therefore, . Thus, we prove that Assumption 2a holds.
. Thus, we prove that Assumption 2a holds.
In fact,  is strictly quasi-concave on X, we have that Assumptions 2b holds.
is strictly quasi-concave on X, we have that Assumptions 2b holds.
(b) It follows from Theorems 12 and 13(a).
(c) We recall that X is convex; therefore, it is contractible and has the fixed point properties. Part (b) implies the proof.
(d) It follows from Theorems 8 and 13(a).
(e) Part (c) implies that  is path-wise connected and
is path-wise connected and  implies that
implies that  . From this, we obtain that
. From this, we obtain that  is infinite and uncountable.
is infinite and uncountable.
(f) Of course, from Theorem 11 and strictly quasiconcavity of  we have
we have .
.
The theorem is proven.
Remark 14. We can easy verify that the Pareto-optimal set  is not convex in general; see also Theorems 13(c) and (e).
is not convex in general; see also Theorems 13(c) and (e).
Remark 15. It is interesting to note that for  the existence of a Pareto-retract multifunction does not necessarily imply the existence of a Pareto-retract function.
the existence of a Pareto-retract multifunction does not necessarily imply the existence of a Pareto-retract function.
To answer the problem of the above remark, we give the following theorem.
Theorem 14. If  are concave on the convex domain X and
are concave on the convex domain X and , then Assumptions 1 and 2a hold. In particular, there exists a continuous Pareto-retract function.
, then Assumptions 1 and 2a hold. In particular, there exists a continuous Pareto-retract function.
Proof. From Theorem 11 it follows that Assumption 1 holds.
Let us assume that . In the proof of Theorem 13(a) we have that if
. In the proof of Theorem 13(a) we have that if  and
and , then
, then . This leads to a contradiction; see also Remark 5.
. This leads to a contradiction; see also Remark 5.
The theorem is proven.
6. Conclusions
We have shown an application of the Maximum Theorem to multi-criteria optimization for the construction of the Pareto-retract mappings and the role of these mappings to analyze the structure of the Pareto-optimal and the Pareto-front sets. Here, we made our considerations in two cases—A general case and a convex case. It is important to note that, in this work, we introduced the concepts of the Pareto-retract multifunction and the Paretoretract function in a multi-criteria optimization problem. By means of these concepts, we have seen how one can use these mappings to analyze the topological properties of the Pareto sets.
The authors see three directions for future research related to this article: One would look for general conditions on the objective functions without the assumption of their concavity; one would analyze specific types of concave or quasi-concave objective functions; and one would study the relationship between the first two.