Domination in Controlled and Observed Distributed Parameter Systems ()
1. Introduction
This work concerns the systems analysis and more precisely a general concept of domination. This notion consists to study the possibility of comparison or classification of systems. It was introduced firstly in [1] for controlled and observed lumped systems and then in [2] for a class of distributed parameter systems. The developed approach concerns separately the input and output operators. Various results are given and illustrated by applications and examples. A duality between the two cases is established. An extension of [2] to the regional case is given in [3]. The regional aspect of this problem is motivated by the fact that a system may dominates another one in a region
, but not on the whole geometrical support 
of the system.
Let us note that in the case of the dual notions of observability and controllability, the literature is very rich. However, the purpose is different and generally, the main problem is how to reconstruct the state of the considered system or to reach a desired state, i.e. to study if a system is (or not) observable or controllable.
In this paper, we consider and we study a more general domination problem in the case of a class of controlled and observed systems [4-6]. The developed approach depends on the different parameters of the considered systems, such their dynamics, their input and output operators. Indeed, we consider without loss of generality, a class of linear distributed systems as follows
(1)
where 
generates a strongly continuous semi-group
(s.c.s.g.) 
on the state
.
,
and 
are respectively the state and the control spaces, assumed to be Hilbert spaces. The system (1) is augmented with the following output equation
(2)
with
, 
is the observation space, a Hilbert space. The operator 
is the dynamics of the system, the operators 
and 
are respectively the input and output operators. The state 
of the system at time 
is given by
(3)
where
(4)
and the observation by
(5)
The first problem consists to study a possible comparison of controlled systems as system (1), with respect to an output operator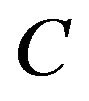
. We give the main properties and characterization results. The case of sensors and actuators is also examined. Illustrative examples and applications are presented and various other situations are examined.
Then, an analogous study concerning the domination of observed systems, with respect to an input operator
, is given. Finally, we study the relationship between the notion of domination and the compensation problem [7,8].
2. Domination for Controlled Systems
2.1. Problem Statement and Definitions
We consider the following linear distributed systems
(6)
(7)
where, for
; 
is a linear operator generating a s.c.s.g. 
on the state space
.
,
; 
is a control space. The systems 
and 
are respectively augmented with the output equations
The state of 
at the final time 
is given by
(8)
where
(9)
The corresponding observation at time 
is given by
(10)
The purpose is to study a possible comparison of systems 
and 
(or the input operators 
and 
if
) with respect to the output operator
.
It is based on the dynamics 
and
, the control operators
, 
and the observation operator
. Without loss of generality, one can assume that 
. We introduce hereafter the corresponding notion of domination.
Definition 1. We say that
1) 
dominates 
(or the pair 
dominates
) exactly on 
with respect to the operator
, if
2) 
dominates 
(or the pair 
dominates
) weakly on
, with respect to the operator
, if
In this situation, we note respectively
Let us give following properties and remarks :
1) Obviously, the exact domination with respect to an output operator
, implies the weak one with respect to
. The converse is not true, this is shown in [2] for 
and
).
2) If the system 
is controllable exactly (respectively weakly), or equivalently
then 
dominates exactly (respectively weakly) any system
, with respect to any output operator
.
3) In the case where
, 
dominates 
exactly (respectively weakly), we say simply that 
dominates 
exactly (respectively weakly). Then, we note
Hence, one can consider a single system with two inputs as follows
(11)
augmented with an output equation
In this case, the domination of control operators 
and 
with respect to the observation operator 
is similar. The definitions and results remain practically the same.
4) The exact or weak domination of systems (or operators) is a transitive and reflexive relation, but it is not antisymmetric. Thus, for example in the case where
, for any non-zero operator 
and
, we have1
, even if 
for
.
5) Concerning the relationship with the notion of remediability [7,8], we consider without loss of generality, a class of linear distributed systems described by the following state equation
(12)
where 
is a known or unknown disturbance. The system (12) is augmented with the following output equation
(13)
The state 
of the system at time 
is given by
where
If the system (12), augmented with (13), is exactly (respectively weakly) remediable on
, or equivalently 
(respectively 
), then 
dominates any operator 
exactly (respectively weakly) with respect to the operator
.
6) For 
and
, one retrieve the particular notion of domination as in [2].
We give hereafter characterization results concerning the exact and weak domination.
2.2. Characterizations
The following result gives a characterization of the exact domination with respect to the output operator
.
Proposition 2. The following properties are equivalent 1) The system 
dominates exactly 
with respect to the operator
.
2) For any
, there exists 
such that
(14)
3) There exists 
such that for any
, we have
(15)
Proof.
The equivalence between i) and ii) derives from the definition.
The equivalence between ii) and iii) is a consequence of the fact that if 
and 
are Banach spaces; 
and 
then
if and only if, there exists 
such that for any
, we have
where
, 
and 
are respectively the dual spaces of
, 
and
.
Concerning the weak case, we have the following characterization result.
Proposition 3.
The system 
dominates 
weakly, with respect to
, if and only if
(16)
Proof.
Derives from the definition and the fact that 
is equivalent to 
It is well known that the choice of the input operator play an important role in the controllability of a system [4-6,9-11]. Here also, the domination for controlled systems, with respect to an output operator
, depends on the dynamics 
and particularly on the choice of the control operators
. However, even if 
(with the same actuator), the pair 
may dominates
. This is illustrated in the the following example.
Example 4. We consider the system described by the one dimension equation
The operator 
generates the s.c.s.g. 
defined by
where
, with
, is a complete system of eigenfunctions of 
associated to the eigenvalues 
.
For
, we have
(17)
Hence, if 
Equation (17) becomes
Let 
and 
.
The corresponding semi-groups, noted 
and
, are respectively defined by
and
Then for 
with 
1) If 
then for any
, we have
consequently, the pair 
dominates the pair 
exactly, and hence weakly.
2) If 
then for any
,
Hence, the pair 
dominates the pair 
exactly (and weakly).
In the next section, we examine the case of a finite number of actuators, and then the case where the observation is given by sensors.
2.3. Case of Actuators and Sensors
This section is focused on the notions of actuators and sensors [4,8,10], i.e. on input and output operators. In what follows, we assume that 
and, without loss of generality, we consider the analytic case where 
and 
generate respectively the s.c.s.g. 
and 
defined by
(18)
and
(19)
where 
is a complete orthonormal basis of eigenfunctions of
, associated to the real eigenvalues 
such that
; 
is the multiplicity of
.
is a complete orthonormal basis of eigenfunctions of
, associated to the real eigenvalues 
such that
; 
is the multiplicity of
.
2.3.1. Case of Actuators
In the case where 
is excited by 
zone actuators 
, we have 
and
(20)
where 
and
;
. We have
(21)
By the same, if 
is excited by 
zone actuators
, we have 
and
(22)
with
, 
,
and
(23)
As it will be seen in the next section, this leads to characterization results depending on 
and the corresponding controllability matrix, and then on the observability one in the case where the observation is given by a finite number of sensors. First, let us show the following preliminary result.
Proposition 5. We have
and
where 
and 
are the corresponding controllability matrices defined by
and
Proof. We have
Therefore, 
if and only if
By analyticity, this is equivalent to
or
where
The proof of the second equality of the proposition is similar.
The following result deriving from proposition 2, gives characterizations of exact and weak domination in the case of actuators.
Proposition 6.
1) 
dominates 
exactly with respect to the operator 
if and only if there exists 
such that for any
, we have
2) 
dominates 
weakly with respect to the operator
, if and only if for any
, we have
Let us note that if
, the domination concerns the operators 
and
, and then the corresponding actuators. This leads to the following definition.
Definition 7. If 
dominates 
exactly (respectively weakly) with respect to the operator
, we say that 
dominate 
exactly (respectively weakly) with respect to
.
In the usual case, the observation is given by sensors. This is examined in following section.
2.3.2. Case of Sensors
Now, if the output is given by 
sensors
, we have
and
We have the following proposition.
Proposition 8. 
dominates 
weakly with respect to the sensors
, if and only if
(24)
where 
and 
are the corresponding observability matrices defined by
and
Proof. 
dominates 
weakly with respect to the sensors
, if and only if, for any
,
implies that
or equivalently, for any
,
we then have the result.
Let us give the following remarks.
1) If
, we have
, for
.
2) One actuator may dominates 
actuators
, with respect to an output operator 
(sensors).
3) In the case of one actuator and one sensor, i.e. for 
and 
we have
and
Then
(25)
4) In the case of a finite number of sensors, the exact and weak domination are equivalent.
3. Application to Diffusion Systems
To illustrate previous results and other specific situations, we consider without loss of generality, a class of diffusion systems described by the following parabolic equation.
(26)
where 
is a bounded subset of 
with a sufficiently regular boundary
; 
and 
for 
is augmented with the output equation
(27)
We examine respectively, hereafter the case of one and two space dimension.
3.1. One Dimension Case
In this section, we consider the systems 
and 
described by the following one dimension equations, with 
and
.
(28)
(29)
admits a complete orthonormal system of eigenfunctions 
associated to the eigenvalues
with 
Each system 
is augmented with the output equation corresponding to a sensor
,
(30)
According to proposition 8, 
dominates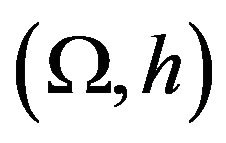 
with respect to the sensor
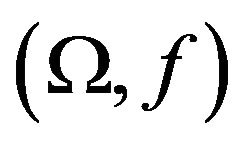, if and only if,
(31)
Let 
such that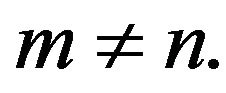 
We suppose that 
and 
are respectively excited by the actuators 
and
, i.e. 
and
.
Then
• 
dominates 
with respect to the sensor 
and
• 
dominates 
with respect to the sensor 
Let us also note that in the one dimension case, any operators 
and 
are comparable. this is not always possible in the two-dimension case which will be examined in the next section.
3.2. Two Dimension Case
Now, we consider the case where 
and the systems described by the following equations
Here, we have 
and
for 
admits a complete orthonormal system of eigenfunctions 
associated to the eigenvalues 
defined by
(32)
and 
are respectively augmented with the output equations
and
Let us first note that:
, then 
is a double eigenvalue, corresponding to the eigenfunctions 
and 
By the same, 
, then 
is also a double eigenvalue, corresponding to the eigenfunctions 
and 
The examples given hereafter show the following situations :
• An actuator may dominates another one with respect to a sensor.
• None of the systems does not dominates the other.
Example 9. In the case where
,
, 
and 
we have
(33)
where 
denotes the y-axis. Therefore 
dominates 
with respect to the corresponding output operator 
On the other hand, for
, 
and 
we have
(34)
where 
denotes the x-axis. Then 
dominates 
with respect to the corresponding output operator 
Example 10. Now, for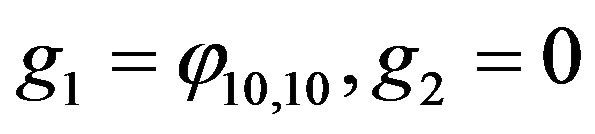
, 
, 
and 
we have
(35)
Then none of the operators 
and 
does not dominates the other.
4. Domination of Output Operators
In this section, we introduce and we study the notion of domination for observed systems (output operators) with respect to an input one. We consider first a dual problem where the control concerns the initial state, and then a general controlled system.
4.1. A Dual Problem
In this section, we examine a dual problem concerning the output operators and observed systems. We consider the system
(36)
The initial state 
depends on an input operator 
and is of the form 
We assume that 
is a linear operator with a domain 
dense in
, a separable Hilbert space, and generates a strongly continuous semi-group 
on the state
.
, 
is a Hilbert space. The system 
is augmented with the following output equations
(37)
(38)
For
; the observations are given by
We have
, with
Its adjoint operator is defined by
Noting 
; 
and considering the dual systems
and
we obtain the following characterization result.
Proposition 11. 
(respectively
) if and only if, the controlled system
dominates 
exactly (respectively weakly).
From this general result, one can deduce analogous results and similar properties to those given in previous sections.
4.2. Domination of Output Operators
We consider the following linear distributed system
(39)
where 
generates a s.c.s.g. 
on the state space
; 
and 
is the control space and the system (S) is augmented with the output equations
where 
is an Hilbert space. The observation with respect to operator 
at the final time 
is given by
(40)
We introduce hereafter the appropriate notion of domination for the considered case.
Definition 12. We say that 1) 
dominates 
exactly with respect to the system (S) (or the pair
) on 
if 
.
2) 
dominates 
weakly with respect to the system (S) (or the pair
) on 
if 
.
Here also, we can deduce similar characterization results in the weak and exact cases. On the other hand, one can consider a natural question on a possible transitivity of such a domination. As it will be seen, this may be possible under convenient hypothesis. In order to examine this question, we consider without loss of generality, the linear distributed systems with the same dynamics 
.
(41)
(42)
where 
generates a s.c.s.g. 
on the state space
;
, 
, 
,
; 
and 
are two control spaces. The systems 
and 
are augmented with the output equations
where
, for
; 
is a Hilbert space. The observations with respect to operator 
at the final time 
are respectively given by
(43)
(44)
By the same, the observations with respect to operator 
at time 
are given by
(45)
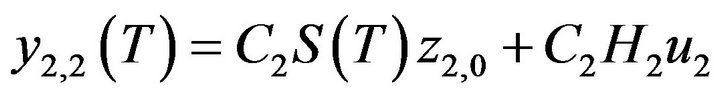(46)
We have the following result deriving from the definitions.
Proposition 13. If the following conditions are satisfied 1) 
dominates 
exactly (respectively weakly) with respect to operator
2) 
dominates 
exactly (respectively weakly) with respect to operator
3) 
dominates 
exactly (respectively weakly) with respect to operator
then 
dominates 
exactly (respectively weakly) with respect to operator
.
We examine hereafter, the relationship between the notions of domination and compensation.
4.3. Domination and Compensation
In this section, we study the relationship between the notions of domination and compensation [7,8]. We consider without loss of generality, the following systems.
(47)
(48)
where 
generates a s.c.s.g. 
on the state space
;
, 
, 
, 
and
; 
and 
are two control spaces. 
and 
are respectively augmented with the output equations
The states of these systems at the final time 
are respectively given by
(49)
where the operators
; 
and 
are defined by
(50)
(51)
The corresponding observations are given by
(52)
(53)
and
. First let us recall the notion of compensation.
Definition 14. The system 
augmented with output equation 
(or
) is 1) exactly remediable on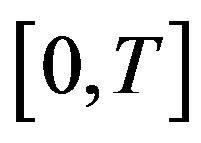 
if for any
, there exists 
such that
, or equivalently
(54)
2) weakly remediable on 
if for any 
and any 
there exists 
such that
, or equivalently
(55)
Here, the question is not to examine if a system is (or not) remediable (for this one can see [7,8]), but to study the nature of the relation between the notions of domination and compensation, respectively in the exact and weak cases. We have the following result.
Proposition 15. If the following conditions are verified 1) 
is exactly (respectively weakly) remediable.
2) 
dominates 
exactly (respectively weakly) with respect to the operator
.
3) 
(respectively 
).
then 
is exactly (respectively weakly) remediable.
We have the similar result concerning the output domination and the remediability notion.
Proposition 16. If the following conditions are satisfied 1) 
is exactly (respectively weakly) remediable.
2) 
dominates 
exactly (respectively weakly) with respect to the operator
.
then 
is exactly (respectively weakly) remediable.
Let us note that this section is a generalization of the previous one where 
has the form
. The results can be applied easily to a diffusion system and to other systems and situations.
NOTES