Photometric Study of Three Short-Period Eclipsing Binaries from the ASAS Catalogue ()
1. Introduction
Eclipsing binary stars are stellar systems consisting of two gravitationally-bound stars orbiting around their common centre of mass, with their orbital motion in a plane sufficiently edge-on to the observer for either total or partial eclipse to occur when one star passes in front of its companion. These stellar systems are very important astrophysical objects because they not only constitute about one half of all stellar populations [1-3], they serve as ideal astrophysical laboratories for the determination of stellar properties such as masses, radii, and temperatures [4]. Their study also yields information on stellar structure and evolution, and the existence of exoplanets [5]. In addition, they can be used for the estimation of cosmic distances and time without external calibration, test the validity of the theory of general relativity (for instance, through the study of binary systems in which one of the component stars is a compact object such as neutron stars and black holes).
Binary systems located in clusters, are even more valuable for study, this because, since all cluster members are presumed to be at the same distance from the Sun, the binaries in a cluster can be used to determine cluster the distance. Furthermore, owing to the fact that they have the same chemical composition and age, but different masses, cluster members are different from one to another. Consequently, a study of binary systems, which are members of a cluster, is important for understanding the evolution of the entire cluster.
Recently, the All Sky Automated Survey (ASAS) [6] has confirmed the detection of some eclipsing binary stars from their all-sky survey. Three of these, namely, ASAS 110609 − 2045.3, ASAS 105331 − 7424.7, and ASAS 130057 + 2120.3 are believed to have very short (<1 day) orbital period and are strongly visible in the visual band. Since the discovery of these objects, no further observational study has been carried out on the systems with a view to characterising their orbital and physical properties. The objective of this study, therefore, is to carry a comprehensive photometric study of these three newly detected short-period eclipsing binaries in order to: 1) determine their orbital and physical parameters, 2) determine the spectral and luminosity class of the binary systems and 3) constrain the structure and evolutionary status of the systems.
The light curve analysis was carried out with the Wilson-Divenney (WD) codes [7], while the period analysis was done with Peranso 2.50 [8]. The visual models were obtained using the BinaryMaker 3.0 software [9].
2. Selection Criteria
We searched the ASAS catalogue and visually inspected several thousand individual light curves of eclipsing binaries and extracted photometric data for those systems that met our specific criteria, which include: 1) those variable systems conclusively established by ASAS as eclipsing binary systems; 2) systems for which no detailed study has been carried out on them; 3) systems with orbital periods of less than one day, selected on the basis that they might be close; 4) systems whose visual magnitude V, ranges between 11 and 13. This is to ensure that we are dealing with systems that meet the exposure time limits for set for the observing telescope optics’ spectral resolving power, as this is directly related to the accuracy of the measurement; 5) systems with light curves that have a primary eclipse depth greater than 0.1 magnitude and those with well defined photometric variations; and 6) systems with light curves where the ratio of eclipse depths are not extreme. This is to ensure that the secondary spectral lines will be readily detectedif spectrometric analysis is to be carried out on these systems.
3. The ASAS Eclipsing Binary Catalogue
The All Sky Automated Survey (ASAS) is blind optical survey that monitors the variability of stars between 8th and 14th magnitude in the visual (V) and infrared (I) bands south of declination +28˚ at the coverage rate of once in 1 - 3 days. The sky coverage became full in 2006. These observations which are automated are carried out at Las Campanas Observatory in Chile. The number stars observed so far is approximately 20 million; the number of detected variable sources is approximately 50,000 out of which 39,000 are new variables. The number of eclipsing binaries detected is 11,099 [6,10]. The ASAS catalogue is publicly available, and can be accessed at http://www.astrouw.edu.pl/asas and http://www.archive.princeton.edu/asas.
4. Observational Data
The following basic information was extracted from ASAS and used in the analysis of respective the binary systems (see Table 1): the epoch of minimum light , the Heliocentric Julian Date (HJD) of measurement, the magnitude of the binary system measured in the visual passband (Vmax), a preliminary orbital period, and the V and I colour indices of the eclipsing system. The corresponding J, H, K colour indices were obtained from 2MASS (Two Micron All Sky Survey) and from these colour indices the spectral class was inferred using the scheme formulated by [11]. From the spectral class, the mean effective temperature,
, the Heliocentric Julian Date (HJD) of measurement, the magnitude of the binary system measured in the visual passband (Vmax), a preliminary orbital period, and the V and I colour indices of the eclipsing system. The corresponding J, H, K colour indices were obtained from 2MASS (Two Micron All Sky Survey) and from these colour indices the spectral class was inferred using the scheme formulated by [11]. From the spectral class, the mean effective temperature,  , of the systems as defined by [12] was determined using the calibration scheme of [13].
, of the systems as defined by [12] was determined using the calibration scheme of [13].

Table 1. List of information extracted from the ASAS catalogue for the analysis of each binary system under study.
5. Data Analysis
5.1. Period Analysis
To obtain the most accurate period of the binary systems, a detailed period analysis of the V-band magnitude data for each system was done using the Date Compensated Discrete Fourier Transform (DCDFT) method embedded in the Peranso software programme. In the programme, the Fourier integral of the raw magnitude data (obtained in the time domain), and date of measurement are transformed in a discretised way into the period or frequency domain taking into account the time of observation as theoretically formulated by [14]. This is summarised below:
In the classical discrete Fourier transform (DFT) method, designated values  taken at time
taken at time  are assigned to a continuous function
are assigned to a continuous function , so that its discrete Fourier transform is written as:
, so that its discrete Fourier transform is written as:
 (1)
(1)
where N is the number of equispaced subintervals  between 0 and t; n designates the discrete times at which samples are taken. The inverse Fourier transform is thus, given by:
between 0 and t; n designates the discrete times at which samples are taken. The inverse Fourier transform is thus, given by:
 (2)
(2)
where 
However, because photometric magnitude data such as those from ASAS are not evenly well-sampled, in our computational period analysis using the Peranso software [8], we used the embedded date compensated discrete Fourier transform (DCDFT) algorithm. The DCDFT method as the name suggests, takes the time of observation into account, meaning that the data no longer has to be regularly sampled and, its underlying principle corresponds to a curve fitting approach using a sinusoid-plus-constant model. Its algorithm is summarised below.
• The spacing between observations which in our case is roughly three days was noted.
• From it the spacing, the Nyquist frequency  (defined as the frequency of a sinusoid exactly one-half that of the sampling frequency) was obtained.
(defined as the frequency of a sinusoid exactly one-half that of the sampling frequency) was obtained.
• The deviations from the mean value  of the differential the magnitude
of the differential the magnitude  were computed and the standard error of measurements noted.
were computed and the standard error of measurements noted.
• For each trial frequency  one coefficient of spectral correlation S was obtained by the following formulae [14]:
one coefficient of spectral correlation S was obtained by the following formulae [14]:
 (3)
(3)
N is the number of observations in the series,  , are the observation dates,
, are the observation dates,  and
and  are the measured
are the measured  referred to their mean values, i.e. shifted in a way such that
referred to their mean values, i.e. shifted in a way such that . The summations are made for
. The summations are made for .
.
• Next, the range of frequencies to be investigated is chosen. Usually, the range is taken from 0 to the Nyquist frequency. Then, an appropriate step to be used in scanning the frequency range is chosen.
• Once the frequency range and the step of scanning are chosen, the value of S for each trial frequency was computed, and the function  plotted.
plotted.
• From the value of  for which S is maximum, the period P, of the variation of the source is obtain as
for which S is maximum, the period P, of the variation of the source is obtain as 
5.2. Light Curve Analysis
The number of geometrical and physical parameters that enters the model of an eclipsing binary star is quite substantial (see Table 2); so that the task of the modelling is to take these parameters and uniquely compute synthetic light curves as predicted by the theory. This is referred to as the direct problem: given the list of parameters, synthetic light curves are uniquely determined. In practice however, photometric modelling involves exactly the opposite: given the observational data, a set of parameters is determined for which the model yields a matching synthetic curve. This is referred to as the inverse problem. In this inverse problem-solving scheme, the solutionseeking process of an eclipsing binary data is formulated as a nonlinear least-squares problem in which observed curves are compared with model (synthetic) curves. In our work, the optimisation of the agreement between the observed and synthetic curves of the systems was carried out computationally using the Wilson-Devinney (WD) code.
As with other minimisation algorithms, the WD algorithm minimises the discrepancy between observational and synthetic curves. This discrepancy is quantified in terms of a cost function  given by
given by

Table 2. A summary of the light curve solutions obtained from the photometric analysis of the binary systems under study.
 (4)
(4)
for the  passband, where
passband, where  and
and  are, respecttively, the number and standard deviation of observational data points in that passband;
are, respecttively, the number and standard deviation of observational data points in that passband; 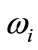 are individual weights,
are individual weights,  are passband weights;
are passband weights; 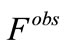 is the observed flux at the given phase and
is the observed flux at the given phase and  is the synthetically-computed flux at the same phase. The weighted variance is given by:
is the synthetically-computed flux at the same phase. The weighted variance is given by:
 (5)
(5)
so that the passband cost function  may be expressed as:
may be expressed as:
 (6)
(6)
The overall cost function is a sum of individual cost functions for each observed curve, thus
 (7)
(7)
where M is the number of curves. If  are properly estimated, the ratio
are properly estimated, the ratio  is of the order of unity and
is of the order of unity and  of the order
of the order . This is used by the code to parameterise
. This is used by the code to parameterise  values as:
values as:
 (8)
(8)
It is this cost coefficient  that directly measure the goodness of fit; if the value is ~1, the discrepancy between the model and observations is small and the fit is satisfactory, and vice versa.
that directly measure the goodness of fit; if the value is ~1, the discrepancy between the model and observations is small and the fit is satisfactory, and vice versa.
While carrying out the optimisation of agreement between the observed and synthetic curves, the orbits were assumed to be circular and so the orbital eccentricity, e of each of the systems was set at zero. The limb-darkening coefficients were interpolated from van Hamme’s table at the respective values suggested for convective and radiative stars [15]. Because of the convective nature of the heat transportation in the envelopes, the values of gravity brightening exponents for the systems were set as  [16] and bolometric albedo
[16] and bolometric albedo  were set at the values suggested for convective and radiative atmospheres by [17]. The adopted adjustable parameters were: the effective temperature of secondary component
were set at the values suggested for convective and radiative atmospheres by [17]. The adopted adjustable parameters were: the effective temperature of secondary component , orbital radius, the orbital inclination i, the fill-out factor, and the monochromatic luminosity of the primary star
, orbital radius, the orbital inclination i, the fill-out factor, and the monochromatic luminosity of the primary star . Since no spectroscopic observations are available for these systems, we used the q-search method to constrain the most important parameter, the mass ratio
. Since no spectroscopic observations are available for these systems, we used the q-search method to constrain the most important parameter, the mass ratio . In order to find the best value of the mass ratio, we executed the code for various assumed values of mass ratio, while keeping in mind that surface potential
. In order to find the best value of the mass ratio, we executed the code for various assumed values of mass ratio, while keeping in mind that surface potential  also changes with respect to the mass ratio.
also changes with respect to the mass ratio.
6. Results
The results obtained from the photometric analysis of each binary system are shown in Table 2, while the light curves, 3-D model and surface outline of the binary systems are given in Table 3. The results of each of the systems are presented below.
6.1. ASAS 110609-2045.3
The photometric magnitude data for ASAS 110,609 − 2045.3 used for this study were those obtained between 30th September 2000 and 23rd July 2008. As evidenced from its light curve (Table 3) we infer that the system is a near-contact binary star of the W Uma type comprising two main sequence stars. In addition, that the nature of the primary eclipse is an occultation, while that of the secondary is a transit. The computed value of the angle of inclination of the system is 80˚ ± 1 to the line of sight. We also established that ASAS 110609 − 2045.3 has a mass ratio of about 0.5, a value that is consistent with other W Uma-type binaries such as RW Com and BD + 07˚ 3142 [18]. The system showed evidence of a third

Table 3. The light curves, 3-D model and surface outline of the binary systems under study. In the light curve, the solid lines are the synthetic curve while the dots trace the observed curve.
light with a third light factor of about 0.5. Using the calibration scheme of [13] the deduced effective temperature of ASAS 110,609 − 2045.3 is in the range of 5800 K - 6200 K, making it a G2V-F7V system. The period was established to be 0.2933 ± 0.0130 days. With this period, the linear ephemeris equation for ASAS 110,609 − 2045.3 was determined to be:
 (9)
(9)
where E corresponds to the cycle number.
6.2. ASAS 105331 − 7424.7
The photometric data for ASAS 105331 − 7424.7 obtained from 22nd November, 2000 to 28th October, 2008 were used in the analysis of the system. The eclipse is inferred to be total as evidenced by the high value of the inclination of the system (about 86˚ ± 2) to the line of sight. We infer from the almost V-shape of the light curve eclipse depth and the 3-D model (Table 1) that ASAS 105,331 − 7424.7 is an over-contact binary star of the W Uma type comprising two main sequence stars. This is consistent with the light curves of other W Umas, such as QX and XY Leonis [19]. During the solution seeking procedure, a third light factor of only 0.1 was established. In the modelling procedure, no evidence of spots or discs was inferred for either component. The photometric mass ratio was determined to be about 0.9, consistent with the computed values of other W Umatype binaries having similar characteristics such as CV Vel [19] and V236 [20]. The effective temperature was computed to be in the range 5200 K - 5300 K, making it a K2V-K0V system. The deduced period of ASAS 105331 − 7424.7 was 0.4825 ± 0.0002, which is consistent with the measured periods of other close binaries such as QX and RW Com [18]. Thus, the derived linear ephemeris equation for ASAS 110609 − 2045.3 is given by:
 (10)
(10)
where E corresponds to the cycle number.
6.3. ASAS 130,057 + 2120.3
Observational data for ASAS 130057 + 2120.3 obtained from the 12th January 2003 to 27th July 2009 were used in the analysis of the system. The results from the analysis of its light curve indicate that ASAS 130057 + 2120.3 is W Uma binary having a mass ratio of about 0.6 in a state of marginal contact. This shallow degree of contact is consistent with other eclipsing pairs such as XY Leo [19]. The light curve variations is slightly above 0.1 mag indicating a low orbital inclination, deduced in this study to be 55˚ ± 1 to the line of sight. The effective temperature of this system was established to be in the range of 6200 K - 6500 K, making it a F7-F5 stellar system, which is consistent with spectral range of other W Uma type binaries. The system showed evidence of third light, with a third light factor of 0.6, however, the presence of spots or discs could not be established for either component.
The deduced period of ASAS 130,057 + 2120.3 was 0.8930 ± 0.0014 days; so that its derived linear ephemeris equation is given by:
 (11)
(11)
where E corresponds to the cycle number.
7. Discussion
An inspection of the observed data curve for the three binary systems reveals scattered phase points, with the primary and secondary minima not coinciding with the zero and 0.5 phase points as expected. This strongly suggests that the period of these systems might actually be varying over the time span of the observational data used. In addition, our study shows that all the systems have a mass ratio greater than 0.4 and so, they should have a trend of increasing period i.e. the systems should evolve towards a semi-detached configuration [21]. This might be especially true for ASAS 130057 + 2120.3 which from its light curve can be inferred to be in a state of marginal contact because of its evolution from a contact state to a semi-detached one according to the thermal relaxation oscillation (TRO) model.
Furthermore, in performing the light curve solutionseeking procedure we assumed that there were no spots or disks on the surfaces of the components of the binaries, and as evidenced from the symmetrical shape of the light curve, the systems do not exhibit any significant O’Connell effect. However, it is important to note here that the case of these binaries in this regard is an exception, since most of the light curves of W Uma-type systems, e.g. V523 Cas [22-24] show asymmetries and irregularities usually interpreted by invoking cool (and/or hot) spots on the surfaces of the two components. Also, the scattered phase points in the observed light curves of the three systems (coupled with their respective third light factor) further suggests the likely presence of a third body, such as an exoplanet or another star altogether, in the neighbourhood of these systems, thus making them a triple system.
Conclusions and Recommendations for Further Work
We have carried out a photometric study of three previously unstudied eclipsing binary stars using data from the ASAS catalogue, namely: ASAS 110609 − 2045.3, ASAS 105331 − 7424.7, and ASAS 130057 + 2120.3. Preliminary result of our study reveals that ASAS 110,609 − 2045.3 a near-contact binary star of the W Uma type comprising two main sequence stars, and that the nature of the primary eclipse is an occultation, while that of the secondary is a transit. The computed value of the angle of inclination of the system is 80˚ ± 1 to the line of sight. We also established that it has a mass ratio of about 0.5, a value that is consistent with other W Uma-type binaries. The modelling also suggests that the system has a third light factor of about 0.5. Its deduced effective temperature is in the range of 5800 K - 6200 K, making it a G2V-F7V spectral system. The period was established to be 0.2933 ± 0.0130 days. The photometric analysis of ASAS 105331 − 7424.7 that ASAS 105331 − 7424.7 is an over-contact binary star of the W Uma type comprising two main sequence stars. The eclipse is inferred to be total as evidenced by the high value of the inclination of the system (about 86˚ ± 2) to the line of sight. During the solution seeking procedure, only a third light factor of just 0.1 was established, and the photometric mass ratio was determined to be about 0.9, consistent with the computed values of other W Uma-type binaries having similar characteristics such as CV Vel and V236. The effective temperature was computed to be in the range 5200 K - 5300 K, making it a K2V-K0V spectral system. Its deduced period was 0.4825 ± 0.0002. For ASAS 130,057 + 21220.3 the analysis of its light curve indicates that it is a W Uma binary having a mass ratio of about 0.6 in a state of marginal contact. This shallow degree of contact is consistent with other eclipsing pairs such as XY Leo. The light curve variations are slightly above 0.1 mag indicating a low orbital inclination, deduced in this study to be 55˚ ± 1 to the line of sight. The effective temperature of this system was established to be in the range of 6200 K - 6500 K, making it a F7V-F5V stellar system, which is consistent with spectral range of other W Uma type binaries. The system showed evidence of third light, with a third light factor of 0.6. The deduced period of ASAS 130,057 + 2120.3 was 0.8930 ± 0.0014 days.
Since this was a first time photometric study of these eclipsing binary stars, the solutions obtained here does not give all the physical properties of the systems as will be expected, and even those obtained here using the photometric technique might not be as precise as required. It is therefore recommended that further photometric and spectroscopic observations and modelling be undertaken to know the possible period changes and constrain the mass ratio and age of the component stars in these binary systems. Astrometric observations would also be useful to detect astrometric wobbles associated with a third body in the system. A combination of this technique and a detection of radial velocity variations in the parent stars (induced by the gravitational tug of the orbiting third body) will confirm or refute the presence of a third body such as an exoplanet or third star in the system.
NOTES