Global Existence, Uniqueness of Weak Solutions and Determining Functionals for Nonlinear Wave Equations ()
1. Introduction
In this paper we study the initial-boundary value problem for the following nonlinear wave equation
(1.1)
with boundary conditions
(1.2)
and initial conditions
(1.3)
where 
constant, 
is a strong structural damping term, 
is nonlinear source term and 
is a nonlinear strain term.
An other version of problems (1.1)-(1.3) was studied in [1-4]. In [1] Chen et al worked that the following initial boundary value problem
(1.4)
(1.5)
(1.6)
has a global solution and there exists a compact global attractor with finite dimension. In [2] Karachalios and Staurakalis studied the local existence for (1.1) with 
ut is a damping term and without nonlinear source term. In [3] Çelebi and Uğurlu gave the existence of a wide collection of finite sets of functionals on the phase space 
that completely determines asymptotic behavior of solutions to the strongly damped nonlinear wave equations. In [4] Chueshov presented the approach of a set of determining functionals containing determining modes and nodes that completely determines the long-time behavior of some first and second order evolution equations.
Similar results of determining modes for similar equations have been obtained in [5-7].
In this article, we take the problem defined by (1.1)- (1.3) which was not investigated in above mentioned articles. Our problem has nonlinear strain and source terms. The control of long time behavior is achieved due to the presence of restoring forces 
In Section 2 under conditions
and 
we prove the global existence and uniqueness of a weak solution u of the problems (1.1)-(1.3). In Section 3 we study determining modes on the phase space 
by using energy methods and the concept of the completeness defect.
2. The Global Existence and Uniqueness of Weak Solutions
Let 
be the usual Hilbert space of square integrable functions with the standard 
norm 
and inner product 
Denote 
the Laplacian operator on L2 with domain 
A is a sectorial operator and that 
is a bounded linear operator defined in 
see [8]. The nonlinear source term 
satisfies the following conditions
there exists a constant 
such that
where 
Finally we denote
with the standard product norm
Define 
in Y by
(2.1)
Then the following Lemma1 is valid [9].
Lemma 1 
is a sectorial operator on Y.
We define a map 
from 
to Y by
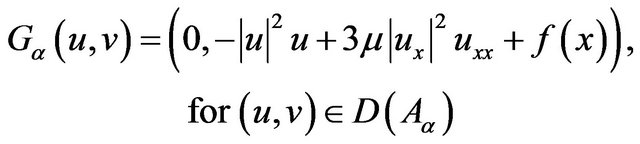(2.2)
where 
Using the Sobolev embedding theorem, we can see that 
is locally Lipschitz continuous. Thus we apply the existence theorem in [8] to get the solutions of initial value problem for the following system in Y:
(2.3)
when
(2.4)
Now, we have the following theorem.
Theorem 2 (Local existence) For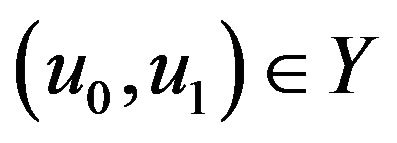 
and 
there exists 
such that 
and 
for a.e. 
and u satisfies (1.1)-(1.3). Moreover, if 
is maximal, then either 
or 
is unbounded on 
Now for the proof of the Theorem 4 (Global Existence) we give the following Lemma 3. In the proofs of Lemma 3 and Theorem 4 (Global Existence) we repeat a similar technique used in [1].
Lemma 3 For 
and 
there exist constants 
such that for 
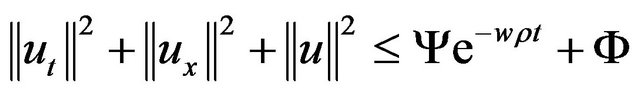(2.5)
where u is the solution of (1.1)-(1.3).
Proof. Let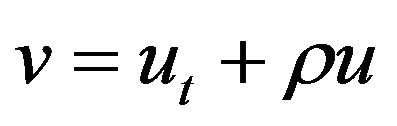 
where 
is a constant to be determined. Thus (1.1) becomes
(2.6)
Taking the inner product of both sides of (2.6) with v and integrating the resulting equation, we have
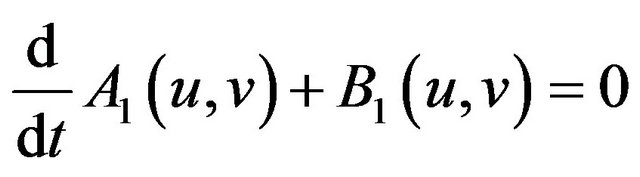(2.7)
where
(2.8)
and
(2.9)
Now we will estimate 
and 
Choose 
such that
(2.10)
where 
is first eigenvalue of the following problem
From (2.8) and (2.9) with
, we get
(2.11)
We use Young inequality, Poincaré inequality and (2.10) in (2.11) we find
(2.12)
Similarly, we obtain
(2.13)
Then (2.7), (2.12) and (2.13) yield
(2.14)
Using Gronwall’s inequality, we have
(2.15)
Since 
we can find that
by using the Sobolev embedding theorem. Thus using (2.13) in (2.15) we obtain
(2.16)
Taking
and choosing 
we get (2.5).■
Now we can prove the global existence of the problems (1.1)-(1.3).
Theorem 4 (Global Existence) For 
there exists a global solution u of problems (1.1)-(1.3) satisfying
.
Proof. In Theorem 2 (Local Existence) we know that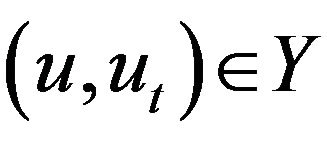 
for 
and
, 
for a.e. 
In Lemma 3 we find that 
and 
are uniformly bounded for all 
Now we prove the global existence of the solution u. To do this we need to show that 
is uniformly bounded for 
Now, taking the inner product of both sides (1.1) in 
with
, we have
(2.17)
Then we multiply both sides of (2.17) by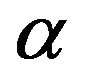 
and add to (2.7) to obtain
(2.18)
Using Poincaré inequality and (2.10) in (2.18), we have
(2.19)
where
(2.20)
and
(2.21)
Then thanks to Young inequality we obtain
(2.22)
Taking 
in (2.22) we get
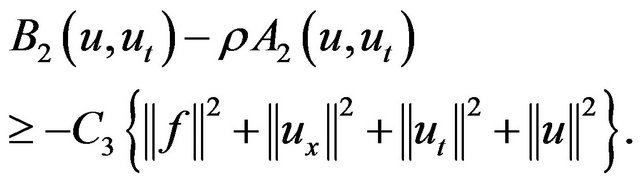(2.23)
Using (2.19), (2.23) and Gronwall’s inequality we get
(2.24)
Thus (2.24) and Lemma 3 imply that 
is uniformly bounded in 
because of
for some constant
and we have
(2.25)
where 
Finally, using Sobolev embedding theorem and Lemma 3 we obtain that 
is uniformly bounded in
■
Theorem 5 (Uniqueness of weak solution) A weak solution of (1.1)-(1.3) is unique.
Proof. Let u and v be two distinct solutions to (1.1)- (1.3) for the same initial and boundary data. We define the difference of these solutions as 
Then from (1.1)-(1.3), w satisfies
(2.26)
(2.27)
(2.28)
Taking the inner product of (2.26) by 
in 
and integrating by parts gives
(2.29)
By means of the inequality
(2.30)
which holds for all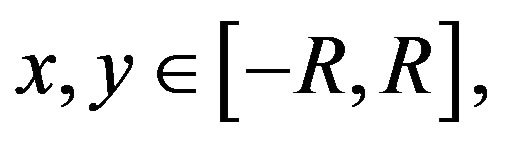 
and 
it follows from (2.29) that
(2.31)
Thus we get
(2.32)
where 
Consequently the differential form of Gronwall’s inequality implies to give 
on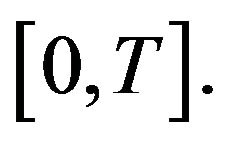
■
3. Existence of Determining Functionals
Now we give some definitions, theorems and corollary for proving existence of determining functionals.
Definition 6 [4] Let 
be a finite set of linear continuous functionals on
We will say that 
is a set of determining functionals for (1.1)-(1.3) when for any two solutions 
with 
and 
the conditions
(3.1)
imply
(3.2)
Definition 7 [4] Let V and H be the reflexive Banach spaces and V be continuously and densely embedded into H. Let 
be a set of linear functionals on V. We define the completeness defect 
of the set 
with respect to the pair of the spaces V and H by the formula
(3.3)
The following assertion gives the spectral characterization of the completeness defect in the case when V and H are the Hilbert spaces.
Theorem 8 [4] Let V and H be the separable Hilbert spaces such that V is compactly and densely embedded into H. Let K be the self-adjoint, positive and compact operator in the space V defined by the equality
for 
Then the completeness defect 
of a set 
of linear functionals on V can be evaluated by the formula
where 
is the orthoprojector in the space V on the annihilator
is the maximal eigenvalue of the operator S.
Corollary 9 [4] Let the conditions of Theorem 8 be hold and let us denote by 
the orthonormal basis in the space V that consists of the eigenvectors of the operator K:
(3.4)
Then the completeness defect of the set of functionals,
can be evaluated by the formula
The following theorem establishes a relation between the completeness defect and the set 
Theorem 10 [4] Let 
be the completeness defect of a set 
of linear functionals on V with respect to H. Then there exists a positive constant 
such that
(3.5)
for any 
where 
is the closed linear span of the set 
in 
the dual space of V and 
is the norm in 
The following version of Gronwall’s lemma is also needed to determine behavior of solutions as 
Lemma 11 [4] Let 
be a locally integrable real valued function on 
satisfying for some
the following conditions
(3.6)
(3.7)
where
. Further, let κ be a real valued locally integrable function defined on 
such that
(3.8)
where 
Suppose that 
is an absolutely continuous non-negative function on 
such that
(3.9)
Then 
as 
Now we can prove the main result concerning existence of a set of determining functionals of solutions to problems (1.1)-(1.3).
Theorem 12 Let 
be a set of linear continuous functionals on the space 
and let 
be a positive number satisfying
where 
R3, R5 positive constants. Then, 
is a set of determining functionals for (1.1)-(1.3).
Proof. Let u and v be two solutions of problems (1.1)- (1.3). Let 
be the difference of these solutions. Thus w satisfies (2.26)-(2.28). Now taking the 
inner product of (2.26) by 
we get
(3.10)
Using (2.30) and Young inequality in right hand side of (3.10) we obtain
(3.11)
On the other hand, the 
inner product of (2.26) by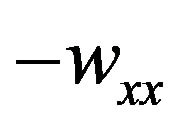 
and integration by parts over 
yields
(3.12)
We assume that for some 
and any small v, v1, 
the nonlinear function 
satisfies
(3.13)
where C is independent of v, v1, v2 [10]. Using (2.30) and (3.13) in (3.12) we have
(3.14)
Using the Hölder, Young and Sobolev inequalities in right hand side of (3.14) we obtain the estimate
(3.15)
where 
is the constant in the Sobolev inequality. Since 
there exists a positive constant D such that 
Then we get
(3.16)
Adding (3.16) to (3.11) and using Poincaré inequality we obtain
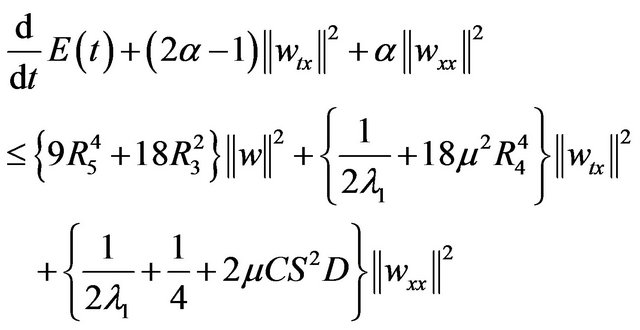(3.17)
where 
are positive constants and
.
Choosing
in (3.17) leads to
(3.18)
Let 
denote the completeness defect between 
and 
and that is
(3.19)
From Theorem 10 we have
(3.20)
for all 
Squaring both sides of (3.20) and using Cauchy’s inequality we obtain
(3.21)
Combining (3.21) in (3.18) leads to
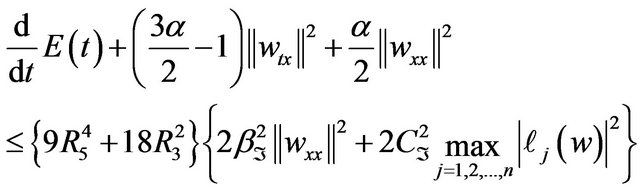(3.22)
Then we choose 
as small as possible so that
Hence, from (3.22) we have
(3.23)
and using Poincaré inequality in (3.23) we find
(3.24)
Now we find upper and lower bounds for the functional 
owing to the Cauchy-Schwartz and the Cauchy inequalities:
(3.25)
Therefore, using (3.25) and from the definition of
, we can find that
(3.26)
Hence, from (3.26) we can obtain that there exists a positive constant
such that
(3.27)
Applying Lemma 11 to (3.27) with
and 
and using a result of Lemma 11 we see that if
tends to zero as 
then 
Thus we obtain that
or
As a result from Definition 6, the set 
defined on 
is a set of determining functionals for (1.1)-(1.3). Therefore we complete the proof of Theorem 12.■
4. Acknowledgements
The author thanks Professor A. Okay Çelebi for valuable hints and discussions.