Numerical Investigation of Effective Heat Conductivity of Fluid in Charging Process of Thermal Storage Tank ()
1. Introduction
The achievable coefficient of performance (COP) of adsorption heat pump systems can be increased by coupling the adsorber in a specific way to a stratified thermal storage tank [1] . In this cycle concept (cf. Figure 1), the COP depends on the degree of mixing in the thermal storage tank. Rational design of a system utilizing such an adsorption cycle with an integrated stratified storage tank requires a transient analysis of the coupled system of adsorber, storage tank, evaporator and condenser as well as external heater and cooler. In order to limit the computational effort involved in system simulations, it makes sense to use a simplified 1-D model of the storage
![]()
Figure 1. Schematic model of the storage tank coupled with adsorption module [3] .
tank. Such models are commonly employed in system simulations of solar thermal heating and cooling systems, see e.g. [2] .
In order to be able to describe the thermal behavior of the storage tank in a system model, the influences of turbulent mixing and advection on the effective thermal conductivity have been investigated by means of a CFD model of thermal storage tank. Effective thermal conductivity is the determining parameter for the description of stratification and mixing in the thermal storage tank. Regarding operation of the thermal storage, the main aim is to maintain thermal stratification by minimizing any mixing effects that may be caused by inertial effects of fluid insertion, turbulence effects or buoyancy effects in case of a temperature mismatch of inserted fluid. For this reason, the convection heat transfer plays an important role in the thermal storage tank. Convection heat transfer includes both diffusion (individual motion of fluid particle in small scale) and advection (bulk fluid motion in large scale). Thermal analysis of the storage tank has been widely studied both experimentally and numerically by a number of researchers. Zurigat et al. [4] studied the influence of different inlet geometries on thermal stratification in a thermocline storage tank. Alizadeh [5] studied the thermal behavior of the storage tank experimentally and numerically. He analyzed specially the discharging process of the storage tank. Nelson et al. [6] presented a one-dimensional transient heat conduction model to describe the decay of the thermocline in a stratified water tank. Bouhdjar et al. [7] studied the influence of the fluid properties and aspect ratios on stratification. Furbo et al. [8] analyzed the entrance effects in solar storage tanks. They performed an experimental and theoretical analysis of water jets entering a solar storage tank. Consul et al. [9] performed the transient numerical simulation of thermal behavior in a storage tank forming part of a thermo-syphon solar heating system. In this study, the influence of the inlet mass flow rate on the degree of thermal stratification during a discharging process has been analyzed. Shah et al. [10] investigated the charging of the storage tank with inlet stratifiers by CFD and experimental work. Altuntop et al. [11] analyzed the effect of using different obstacles on thermal stratification in a cylindrical hot water tank. Andersen et al. [12] analyzed the thermal stratification devices for hot water heat stores by means of CFD and experimental study. They investigated the inlet stratification pipe effect with a limited number of operating conditions appearing in solar collector loops. Different charging systems for maintaining the stratification in thermal storage tanks are described and analyzed in the previous works. One of the prevalent stratifier systems consists of pipes with vertically arranged outlets. This patented charging system is marketed by German company Sailer GmbH [13] . According to the fluid density, incoming fluid can flow to the proper tank layer matching its temperature. In the present work, the same construction of stratification pipe with vertical openings has been implemented for the charging of the storage tank. There are different reasons that diminish the thermal stratification in the storage tank. These are as follows,
1) Plume entrainment
Near the inlet region, momentum effects of the fluid entering the storage are commonly more important than buoyancy effects. In such situations, fluid plume can be defined as fluid jet. Because of the velocity gradient and shear effect, the surrounding fluid will be entrained, resulting in an increased mixing effect [14] . In the present work, the entrainment of the fluid from the tank to stratification pipe through the openings has been described as suction effect.
2) Inlet jet mixing
Because of the high momentum of the entering fluid, turbulent mixing in the near of the inlet leads to a locally increased mixing. One of the advantages of the stratification pipe for the charging process is that turbulent kinetic energy can be partly bounded inside of the stratification pipe. Therefore, the mixing effect influences have been more restricted.
3) Conduction heat transfer within the storage medium and storage tank wall
Conductive heat transfer tends to reduce the temperature gradient and consequently more destratification. In the current study the storage tank for application in the adsorption heat pump cycle has been simulated and its charging process has been investigated. The charging of the storage tank has been carried out through a rigid inlet stratification pipe with a similar structure to the stratification pipe marketed by Sailer GmbH [13] . The main aim of using the stratification devices is the suppression of mixing effects due to high inflow velocities. This stratification pipe also enables an inflow at different heights of the storage due to the influence of buoyancy. The inlet stratification pipe has an inner diameter of 34 mm and an outer diameter of 89.4 mm and has been mounted vertically in the storage tank. Fluid arises through the stratification pipe in the vertical direction and can leave the pipe through the openings at different levels. Vertical distance between each two openings is 9.5 mm.
2. Modeling and Simulation
Figure 1 shows the schematic model of storage tank in adsorption heat pump cycle. The geometry of the cylindrical tank used for the current investigation is described as follows:
・ Height: 1.9 m;
・ Diameter: 19 cm;
・ Width of the heater and cooler ports: 0.41 cm (as ring around tank perimeter);
・ Heater outlet position: 57% of the storage height from the bottom (1.08 m);
・ Heater inlet position: at the top of the storage tank;
・ Cooler outlet position: 25% of the storage height from the bottom (0.47 m);
・ Cooler inlet position: at the bottom of the storage tank.
The development potential of this adsorption heat pump cycle bases upon the internal heat recovery between adsorption and desorption processes [1] . The thermal storage tank functions as intermediate heat storage between two half cycles of adsorption and desorption. In Figure 2, the storage tank CFD model with the implemented stratification pipe and boundary conditions in an axisymmetric domain has been depicted. The very high aspect ratio (height/diameter) of 10 has been chosen for this tank to decrease the temperature gradient for a certain temperature difference inside of the storage tank and therefore to reduce the heat transfer process due to conduction. Reduced heat transfer maintains the stratification level and causes less mixing effect. It should be noted, however, that such a large aspect ratio may increase the thermal losses of the tank to its environment.
The function of the heater cycle is to provide that part of the desorption heat, which is not covered from the released heat during the adsorption half cycle. The heat transfer fluid is extracted at the level of the heater position (heater outlet in CFD model) and after heating up, will be inserted at the top of the tank. The function of cooler cycle in this application is to provide a heat sink. The cooler cycle absorbs that part of the released heat during the adsorption that will not be used for the desorption half cycle.
2.1. Heat Transfer Fluid
The storage tank is considered here for a high-temperature adsorption cycle utilizing zeolite 13X/water as the
![]()
Figure 2. Storage tank 2-D axisymmetric domain with implemented stratification pipe and boundary conditions.
adsorption pair [1] . Therefore, the heat transfer fluid used in the storage is a synthetic thermal oil, Marlotherm LH [15] . Its properties such as density, specific heat capacity, thermal conductivity and viscosity have been defined in a piecewise linear manner in Ansys Fluent CFD model. The thermal conductivity of Marlotherm LH in the applied temperature range varies between 0.111 and 0.129 ). The viscosity ranges from 0.0004 to 0.00256
). The viscosity ranges from 0.0004 to 0.00256 .
.
2.2. Numerical Method
Commercial CFD code Ansys Fluent 14.0 based on the finite volume method has been used for the simulation. The fluid cylindrical domain in the storage tank has been simulated as a 2-D axisymmetric CFD model. The pressure-based coupled algorithm has been applied in order to solve the flow governing equations. Second order upwind discretization scheme for momentum, turbulent kinetic energy and dissipation rate has been employed in the computation. The fluid domain has been discretized with about 400,000 cells, which is a combination of block-structured and unstructured grid. Second order implicit time discretization has been applied for the transient formulation of the charging process with a time step of 0.2 second.
2.3. Initial and Boundary Condition
Since there is no single state of the storage that could be considered as representative of the whole adsorption/ desorption cycle, an arbitrary state that might occur during the adsorption half cycle has been selected for this case study. The fluid inside of the storage tank has been initialized with linear function of temperature with 38˚C at the bottom of the tank to 200˚C at the top of the tank (as shown in Figure 3). The storage has been charged from the bottom through the stratification pipe with charging fluid at 119˚C and 0.2 kg/s mass flow rate. Simultaneously, the heater and cooler extract and reinsert the fluid with 20 percent of the storage charging mass flow rate. Therefore, the solution domain contains six different boundary conditions for inflow and outflow, and also wall and symmetry axis. In the cooler cycle, fluid will be extracted from the storage and will be cooled down to the fluid temperature at the bottom of the tank (38˚C) and enters again to the tank at the bottom. In the heater cycle, similarly after fluid extraction, it will be heated up to fluid temperature at the top of the storage (200˚C) and enters again to the tank at the top.
2.4. Turbulence Modeling
The modified version of  RANS (Reynolds Averaged Navier-Stokes) model suggests alternative eddy viscosity formulation and dissipation rate transport equation, which shows better prediction of the flow structures with round jet and recirculation. The realizable
RANS (Reynolds Averaged Navier-Stokes) model suggests alternative eddy viscosity formulation and dissipation rate transport equation, which shows better prediction of the flow structures with round jet and recirculation. The realizable 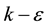 model has been used in order to compute the turbulent viscosity. Transport equations for turbulent kinetic energy and turbulent energy dissipation rate have been represented in Equations (1) and (2), respectively [16] .
model has been used in order to compute the turbulent viscosity. Transport equations for turbulent kinetic energy and turbulent energy dissipation rate have been represented in Equations (1) and (2), respectively [16] .
 (1)
(1)
 (2)
(2)
where

In transport equations of turbulent kinetic energy and turbulent energy dissipation rate,  and
and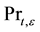 are the turbulent Prandtl numbers for
are the turbulent Prandtl numbers for  and
and .
.
In the 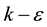 turbulence model, turbulent eddy viscosity is computed by means of turbulent kinetic energy and turbulent energy dissipation rate via the Equation (3):
turbulence model, turbulent eddy viscosity is computed by means of turbulent kinetic energy and turbulent energy dissipation rate via the Equation (3):
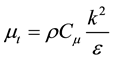 (3)
(3)
The value of 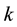 and
and ![]() is determined directly from differential transport equations for the turbulence kinetic energy and turbulent energy dissipation rate. The turbulent kinetic energy contour in Thermal Energy Storage has been shown in Figure 4.
is determined directly from differential transport equations for the turbulence kinetic energy and turbulent energy dissipation rate. The turbulent kinetic energy contour in Thermal Energy Storage has been shown in Figure 4.
The effective thermal conductivity due to turbulent mixing in the fluid domain is calculated from the Equation (4),
![]() (4)
(4)
In Equation (4) ![]() is fluid thermal conductivity,
is fluid thermal conductivity, ![]() turbulent eddy viscosity and
turbulent eddy viscosity and ![]() turbulent Prandtl number.
turbulent Prandtl number.
![]()
Figure 3. Initial temperature distribution in thermal storage tank.
![]()
![]()
Figure 4. Turbulent kinetic energy contour after 4 seconds charging.
2.5. Buoyancy Modeling
Due to the temperature difference and, therefore, density difference, the natural buoyancy results in a buoyancy- driven flow in thermal energy storage.
In simulation of TES, the buoyancy term has been modeled by means of a body-force term in momentum equation (Boussinesq Model). This body-force term has been shown in Equation (5) [16] .
![]() (5)
(5)
where ![]() is the reference density which is usually considered as averaged density value in simulation domain and
is the reference density which is usually considered as averaged density value in simulation domain and ![]() the gravitational acceleration.
the gravitational acceleration.
2.6. Calculation of Advection Effect in Charging Process of the Storage Tank
Heat advection caused by the bulk fluid motion contributes to effective thermal conductivity with an additional part. This part of effective thermal conductivity has been calculated for the current selected case of charging process in adsorption heat pump cycle. The equations used for the calculation of advection part in effective thermal conductivity have been represented in Equation (6).
![]() (6)
(6)
where ![]() is the horizontal cross section of thermal storage tank between outer diameter of the stratifica-
is the horizontal cross section of thermal storage tank between outer diameter of the stratifica-
tion pipe and storage tank wall. ![]() is the average value of the temperature gradient over the horizontal cross section of the storage tank.
is the average value of the temperature gradient over the horizontal cross section of the storage tank.
3. Results and Discussion
The main mechanisms influencing the transient development of the temperature profile in a Thermal Energy Storage are heat transport process, mixing of the charging fluid with stored fluid, and local turbulence because of stratification [17] . From the temperature distribution inside of the storage it can be seen that the region above to the heater outlet doesn’t show a significant mixing. The fluid at the extraction level of heater cycle has been extracted (heater outlet in CFD model) and the fluid with the same temperature as the upper layer in tank has been introduced at the upper part. Because of the insertion at the heater inlet and extraction at the heater outlet, temperature profile has been shifted to the left and with the time progress, this displacement increases. This behavior can also be observed by ideal plug flow charging model. The average values of the temperature between outer diameter of the stratification pipe and storage tank wall have been demonstrated in Figure 5. It shows that the fluid insertion level from stratification pipe to storage tank is about 1.1 m from the bottom of the tank which is close to the heater outlet position (as shown in Figure 6). Because of high momentum of entering fluid in stratification pipe an overrun of the fluid jet and higher insertion height from stratification pipe to the storage is observed. At this height, the initial, linearly stratified temperature profile starts to break. At lower levels especially until cooler outlet, mixing leads to destroy the linear stratification with higher intensity.
3.1. Analysis of Effective Thermal Conductivity Due to Advection
In the 1-D plug flow model of thermal storage tank in adsorption heat pump system simulation, the effect of all heat transfer processes can only be taken into account as an effective heat conduction between adjacent fluid
![]()
Figure 5. Average temperature distribution in storage tank for different charging times in transient simulation.
![]()
Figure 6. Temperature contour and velocity vector with the magnification of the insertion region from stratification pipe to the storage tank after 60 s charging.
layers. In the current numerical investigation of the charging process, advection due to the bulk fluid flow has been considered as another heat transfer mechanism, which leads to stronger mixing in the tank. In order to calculate the advection part of the effective thermal conductivity according to Equation (6), a User Defined Function (UDF) has been applied to the CFD model. The UDF has been interpreted and executed to calculate the desired variables in Equation (6). The advective heat transfer part has been integrated over horizontal surfaces at different heights of the tank. In addition, the production of horizontal surface and average value of temperature gradient in axial direction has been exported over different horizontal surfaces at different heights of the tank. By means of these parameters, the effective thermal conductivity due to advection has been calculated at different charging times.
3.2. Analysis of Effective Thermal Conductivity Due to Turbulence
Turbulent diffusion in fluid flow in TES enhances the mixing due to increasing the transport rate of momentum, which leads to homogenization. On the other hand, enhanced energy transport rate due to turbulence causes an intensified heat transfer process. This enhancement can be considered on the basis of additional thermal conductivity called effective thermal conductivity due to turbulent motions.
In transient simulation, effective thermal conductivity in the storage with the realizable ![]() turbulence model has been calculated and the average values over the whole horizontal area at different storage heights have been plotted (Figure 7). The results demonstrate also the maximum value in the region of main flow insertion from stratification pipe into the storage. Turbulent viscosity contour depicted in Figure 8 demonstrates the highest value of turbulent viscosity, and consequently, effective thermal conductivity due to turbulence in this region. The comparison of two parts of the effective thermal conductivity reveals that the effective thermal conductivity part due to turbulence is considerably higher than effective thermal conductivity part due to advection except for a small region at the lower part of the storage tank (as shown in Figure 9). Computation results with SST
turbulence model has been calculated and the average values over the whole horizontal area at different storage heights have been plotted (Figure 7). The results demonstrate also the maximum value in the region of main flow insertion from stratification pipe into the storage. Turbulent viscosity contour depicted in Figure 8 demonstrates the highest value of turbulent viscosity, and consequently, effective thermal conductivity due to turbulence in this region. The comparison of two parts of the effective thermal conductivity reveals that the effective thermal conductivity part due to turbulence is considerably higher than effective thermal conductivity part due to advection except for a small region at the lower part of the storage tank (as shown in Figure 9). Computation results with SST ![]() turbulence model show the similar trend of effective thermal conductivity inside of the storage tank. Although this model predicts relatively smaller values in regions of main flow insertion from stratification pipe to the storage and heater cycle, however, the turbulent part of effective thermal conductivity still plays a key role in comparison with advection part.
turbulence model show the similar trend of effective thermal conductivity inside of the storage tank. Although this model predicts relatively smaller values in regions of main flow insertion from stratification pipe to the storage and heater cycle, however, the turbulent part of effective thermal conductivity still plays a key role in comparison with advection part.
4. Conclusions
The effective thermal conductivity due to turbulence and advection in the thermal storage tank is an important parameter influencing the performance of the whole adsorption heat pump system under consideration. It accounts for convection effect and turbulent mixing in the storage tank. Therefore, it can only be determined for a specific geometry of tank, inlet and outlet ports, initial and boundary conditions. For any given geometry, it depends on the fluid charging volume flow rate, heat transfer fluid, and the temperature profile in the storage tank. The results reveal that in this CFD model and under the conditions chosen here, the influence of the turbulence part on the effective thermal conductivity is much more important compared to the advection part. Turbulent mixing leads to more intense mixing effect and destratification and shows stronger influence on the effective thermal conductivity. Under these circumstances, the results can also be expected to strongly depend on the details of the turbulence model used, and therefore should be treated with caution. A reassessment of these results with more fine-grained turbulent flow computation methods such as Large Eddy Simulation (LES) or Direct Numerical Simulation (DNS) would be welcome.
![]()
Figure 7. Contour of effective thermal conductivity (W/mK) due to turbulence after 60 s of charging.
![]()
Figure 8. Turbulent viscosity contour (kg/m∙s) in the storage outlet region after 60 s of charging.
![]()
Figure 9. Comparison of effective thermal conductivity due to turbulence and advection after 60 s of charging.
Application of an inlet stratification pipe restricts the impact of the turbulent mixing partly to the inner region of that pipe and therefore would be advantageous in order to avoid higher level of turbulent mixing and effective thermal conductivity inside of the storage tank. One of the demonstrative disadvantage of the applied geometry for the stratification pipe is the entrainment effect which leads to suction of the fluid from storage to the stratification pipe.
Acknowledgements
H. Taheri would like to sincerely thank Karlsruhe Institute of Technology for providing a scholarship (Rektorstipendium), and also Balazs Pritz for his constructive comments. F. P. Schmidt gratefully acknowledges project funding by the state of Baden-Württemberg (ZO-III Initiative) through the Project Management Agency Karlsruhe (PTKA-BWP).
Nomenclature
Symbols
![]()
![]() Surface area
Surface area
![]()
![]() Specific heat
Specific heat
![]()
![]() Constant coefficient of
Constant coefficient of ![]() turbulence model
turbulence model
![]()
![]() Specific heat at constant pressure
Specific heat at constant pressure
![]()
![]() Turbulent viscosity coefficient
Turbulent viscosity coefficient
![]()
![]() Generation term
Generation term
![]()
![]() Gravitational acceleration
Gravitational acceleration
![]()
![]() Storage tank height
Storage tank height
![]()
![]() Thermal conductivity
Thermal conductivity
![]()
![]() Turbulent kinetic energy
Turbulent kinetic energy
![]() Pressure
Pressure
![]()
![]() Prandtl number
Prandtl number
![]()
![]() Heat energy
Heat energy
![]()
![]() Heat transfer rate
Heat transfer rate
![]()
![]() Source term
Source term
![]()
![]() Mean strain rate tensor
Mean strain rate tensor
![]()
![]() Temperature
Temperature
![]() Time
Time
Velocity
![]()
![]() Velocity components
Velocity components
![]() Volume
Volume
![]()
![]() Dissipation term
Dissipation term
![]()
![]() Coordinates
Coordinates
Greek Symbols
![]() Density
Density
![]()
![]() Dynamic viscosity
Dynamic viscosity
![]()
![]() Kinematic viscosity
Kinematic viscosity
![]()
![]() Turbulent kinetic energy dissipation rate
Turbulent kinetic energy dissipation rate
Subscripts
cs Cross section
conv Convection
eff Effective
hor Horizontal
ref Reference
![]() Turbulent
Turbulent
![]() Turbulent kinetic energy
Turbulent kinetic energy
![]() Turbulent kinetic energy dissipation rate;
Turbulent kinetic energy dissipation rate;
![]() Buoyancy.
Buoyancy.
Superscripts
![]() Mean value; time averaged component
Mean value; time averaged component
![]() Vector
Vector
![]() Time derivative
Time derivative
List of Abbreviations
COP Coefficient of Performance
CFD Computational Fluid Dynamics
RANS Reynolds Averaged Navier-Stokes Equation
UDF User defined function
1-D One Dimensional
2-D Two Dimensional