A WSN-Based System for Country Border Surveillance and Target Tracking ()
Received 7 January 2016; accepted 11 March 2016; published 14 March 2016

1. Introduction
The large scale evolution in wireless sensor network technology makes it possible to implement wireless sensor networks (WSNs) within a wide range of applications including healthcare monitoring, battlefield surveillance, and physical or environmental conditions observation [1] [2] . In particular, sensors are able to gather information about a target moving in a region of interest and collaborate to report their measurements/information to an analysis center, where tracking capabilities are provided.
A target is an entity (a moving object, individual, or animal) whose state and activity are of interest for an application. Identifying a target while crossing a border by its particular features, detecting its path over a period of time and predicting its moves and positions in the future constitute the major hard tasks to address in tracking targets. In addition, tracking using sensor networks is complex due to the processing, scheduling, communication, and energy constraints it faces. In particular, the sensors should share data and cooperate to perform data fusion and event relaying appropriately.
To accomplish target tracking, the WSNs have implemented several techniques including: a) data acquisition techniques achieving the monitoring task by sampling data and measuring characteristics related to target locations and activities over time; b) scheduling techniques allowing an optimized use of energy while allowing larger sensor lifetime; and c) maintenance techniques offering an interesting level of tracking quality. One can notice that these techniques, as published in the literature, were based on the assumption that there are enough sensors that are capable of sampling targets’ features across time. Nevertheless, studies on WSNs have shown that this assumption does not hold all the time because of initial deployment weaknesses, energy consumption modes, or external factors including sensor failures and physical attacks [3] - [5] .
Since target tracking is a realistic and dynamic estimation scheme, in its general form, an efficient tracking needs to lay down a “theory” capable of controlling the measurements, the estimation and the errors experienced within the processes of prediction and approximation. Moreover, target tracking systems in border surveillance systems should be able to comply with more constraining features, such as operating under real conditions, collaborating to help efficient interception of trespassers, and providing surveillance continuity and protection. One can notice, however, that most of the proposed solutions do not provide all this and handle only some parts of it.
In this paper, we propose a distributed and prediction capable scheme, called Border Cooperative Predictive Tracking protocol (BCTP), to accurately track mobile targets within a given area, which has the form of large thin strip along a borderline. The scheme provides a technique to deploy wireless sensor networks in the strip under a mathematically controlled random mode. The latter assumption is realistic since a similar scheme has been made available, in general, along with a mathematical control of the coverage they allow [6] . Our protocol provides power conservation as one of the key design guidelines and controls the continuity of tracking. The protocol assumes that most of the sensor nodes, except a line (or a few lines) parallel to the border, stay in a sleep mode (with their transmitting and sensing function shutdown) for most of the time, waiting for a wake up signal.
The contribution of this paper is three-fold: a) Given the number of targets to detect, the protocol provides a distributed mechanism for determining the set of sensors to wake up in the vicinity of the future positions of the detected targets, until complete area crossing; b) to minimize the energy consumption during tracking, the protocol reduces the number of sensors to only some among those that are expected to have the target in their range at the moment of wakeup; c) a mathematical model is developed to control tracking continuity and estimate the exit time and exit segment of any target from the strip built along the frontier; and d) a mathematical model is built to control the deployment scheme of the WSN capable of guaranteeing a high probability of tracking continuity.
The remaining part of this paper is organized as follows. Section 2 discusses the limits of the existing target tracking solutions for border surveillance and reviews the tracking techniques developed for WSNs. Section 3 develops the requirements for an efficient tracking system. Section 4 presents the Border Cooperative Predictive Tracking scheme. Section 5 builds the mathematical models for target tracking. Section 6 defines estimation techniques for exit segment determination. Section 7 constructs a mathematical model capable of determining the probability of target tracking continuity. Section 8 discusses numerical experiments of the protocol and mathematical model. Section 9 concludes this paper.
2. State of the Art
The efficiency of WSN-based surveillance systems highlights two major objectives to achieve: first, it should build on a deployment scheme capable of offering total coverage of the area under monitoring so that any target entering the area is detected. Second, it should be able to track moving objects of interest in the area. Both goals have received an extensive attention during the last decade. Efficiency also needs that sensors should optimize the energy consumption, since the aim of an efficient tracking should ensure both continuous monitoring and energy conservation. To this end, the sensors should be able to dynamically move between a sleeping status and an active status. In a target tracking application, for instance, the sensors that can detect a target, appearing in the sensor’s vicinity at a particular time, must be in an active state.
2.1. WSN-Based Border Surveillance Systems
Several recent works have discussed the design of country border surveillance systems based on WSNs. A majority of the proposed solutions have displayed the WSN nodes as a linear network, so that every movement going over the barrier (or line) of the sensors is detected [7] - [9] . Compared to full coverage, the barrier coverage provided by a perfect linear deployment requires only a few sensor nodes, but experiences more radio disconnections, due to sensor failure and energy depletion. In addition, this kind of linear architecture presents two drawbacks: first, it does not permit the tracking of intruders, since the intruders are only detected when they cross the line of sensors and their future movements cannot be tracked. Second, the sensor nodes are not able to locally determine whether the barrier full coverage is ensured.
On the other hand, solutions using k-barrier coverage require that all crossing paths in the monitored region around a spatial line are covered by at least k distinct sensor nodes. Such solutions include the 3-layered hybrid network architecture for border patrol, called Bordersense that has been proposed in [10] . Bordersense deploys advanced sensor networking technologies utilizing multimedia sensor nodes, mobile sensor nodes, and scalar sensors, which could be installed underground or above the ground. The high cost of the deployment of multimedia sensors (including cameras) makes Bordersense hard to deploy for larger borders and the uniformity of sensor distribution difficult to achieve, except when an appropriate deployment scheme is designed taking into consideration the environment complexity.
The case of border surveillance when sensors are randomly and uniformly deployed has been also investigated in a few works. Even though uniform sensor deployment is useful in theoretical scenarios, it remains unrealistic in the real cases, where a non-uniform placement is experienced due to several environmental features such as dense vegetation and rough terrain. In addition, most of the published works do not provide a mathematical control of the sensing coverage, so that coverage hole can be detected and repaired.
On the hand, the authors in [11] presented the design of border surveillance solutions using wireless sensor networks while providing the following contributions: first, a global network architecture for border surveillance based on three types of components operating in a thick line architecture was set up along the border. Second, a deployment strategy that copes with many constraints on the WSN operation, coverage maintenance, connectivity preservation, and routing quality of service was designed. Finally, a mechanism of routing management to ensure efficient data relaying and reporting between the different node layers. Even though target tracking and target moves prediction were not addressed in [11] , the solution presents interesting aspects such the mathematical control of the sensing and communication coverage quality.
On the other hand, one can see that some other proposed frameworks for border surveillance assumed that a line- (or a thick-line) based WSN offering barrier or k-barrier coverage is provided. Under this assumption, the solutions attempted to reduce the number of needed sensors to monitor the crossing of a given border; but, the improvement is obtained at the expense of efficiency reduction and tracking limitation. In other words, line- based deployment at best ensures the detection of all intrusion attempts, but will not allow to take an internal decision about tracking the intruders. Furthermore, the coverage provided by these solutions is not realistic due to environmental factors and sensors dropping techniques (air-dropping or manned dropping, for example). Another limitation of the proposed models is the silence they observe about the connectivity and prompt reactivity issues.
In addition, one can see that target tracking under surveillance systems presents very special constraints with respect to the common WSN-based monitoring of two dimensional areas. Indeed, tracking in border surveillance should be done in real-time mode, should be available all the time, should be continuous, and should be able to help predicting the exit time and zone for the monitored area. The objectives of the next subsection are to survey the works performed in WSN-based target tracking approaches and to discuss their limits with regards to the aforementioned differences.
2.2. WS-Based Target Tracking Solutions
We can classify the target tracking techniques into several categories, based on the sensor activation modes, the network topologies and the sensor partition techniques they use. Node activation can be naïve, randomized, selective, based on trajectory prediction, or duty cycled [12] . Naïve activation based tracking techniques, where all nodes are in active (or tracking) mode all the time, are among the simplest and general tracking techniques. In such context, the sensing nodes report their local measurements to the sink node. The latter follows the target motion in relation with the reported measurement and attempts to predict the target positions in the future. Naive activation ensures high tracking quality; but, it offers the worst energy consumption and provides heavy communication to the sink node, since sensors are all the time sensing, estimating, reporting, or data relaying.
Tracking methods using naïve activation are not robust because the WSN they use is more prone to energy depletion, traffic congestion, sensor failure, and even security attacks. In the following, we consider the other solutions and mainly discuss two major overlapping categories; namely, the hierarchical and prediction-based classes of tracking [13] [14] . We also analyze their drawbacks with respect to border surveillance requirements.
2.2.1. Hierarchical Tracking Methods
In a hierarchical tracking method, the WSN is organized in such a way where sensors in the vicinity of a target must be able to detect it and report back to the sink node using the network hierarchy. Therefore, the sensors should be able to relay the messages of other sensor nodes, by acting as repeaters, and to support data processing results on behalf of the other senor nodes, when needed. Hierarchical tracking methods can be classified into three categories: tree-based tracking, cluster-based tracking, and hybrid methods.
In tree-based target tracking, sensor nodes are organized in a hierarchical tree (or sometime in a graph), where nodes are sensors and edges are links between sensors that can directly communicate with each other. In particular, in STUN (Scalable tracking using networked sensors), a tree-based approach in which a cost is assigned to each link, computed on the Euclidean distance between the two communicating nodes, is used [15] . The leaf nodes serve for tracking the targets and sending the collected data to the sink through intermediate nodes on the tree. Intermediate nodes keep a record on the detected target and send updated information to the sink, whenever there is a change in that record. Moreover, in [16] , Zhang et al proposed a tracking technique, called Dynamic Convoy Tree-Based Collaboration (DCTC), where spanning trees are used to detect and track the mobile targets and monitor their surrounding area. The tree is dynamically configured to add nodes and exclude other nodes as they become far away from the related target. One can observe that STUN and DCTC experience high costs in builds and maintaining the trees.
Various other tree-based techniques have been developed [17] . Some of these works present limitations such as the dependence on the tree structure for the network topology. In particular, organizing sensor nodes in logical trees, location updating, and querying may present unacceptable costs. Moreover, when a target is discovered, the source sends a wake request to sensor nodes and the nodes in the vicinity to the target replies back. To detect moving target continuously, the spatial neighbors of near sensor node are wake up.
On the other hand, cluster-based tracking methods assume that the WSN is partitioned into clusters to support collaborative tracking processes using cluster heads. Three categories of cluster-based methods can be distinguished; they are: the static clustering, dynamic clustering, and space time clustering. In the static clustering methods, the nodes are partitioned into clusters on network deployment. The cluster size, cluster head, and cluster members are static. The main advantage of a static clustering method is its simplicity. Its major disadvantage stems from the fact that it is not fault tolerant. For example, if a cluster head is out of energy, all the sensors belonging to its cluster will not be able to operate until a new cluster head is elected.
Low-Energy Adaptive Clustering Hierarchy (LEACH) was developed with the desire to reduce energy consumption in the WSN [18] [19] . A sensor node in LEACH detecting a target sends its data to its cluster-head. The latter aggregates and compresses the data it collects and sends it to the sink node. Since a cluster head requires more energy during operation than the other sensors belonging to its cluster, LEACH allows random rotation of cluster heading to balance energy consumption in every cluster in the WSN.
Alternatively, the Continuous Object Detection and Tracking (CODA) mechanism considers that the WSN uses a static backbone comprising a number of static clusters built during the initial network deployment step. In each cluster, any sensor detecting the moving targets in its vicinity transmits the detecting information directly to the cluster head [20] . Two advantages characterize CODA: the communication overhead is substantially reduced and an explicit header election scheme is not required.
Unlike static clustering approaches, dynamic clustering methods allow the formation of a cluster on the occurrence of certain events of interest such as the approaching of a target to the area of a group of sensors. Examples of dynamic cluster-based tracking include information-driven sensor querying (IDSQ), RARE, and DELTA [21] - [23] . IDSQ supposes that each node in the network can locally estimate the cost of sensing, processing and data communication to the other sensors. It also allows to determine dynamically which sensor is most appropriate to perform target detection.
RARE approach reduces the number of sensors contributing in tracking by preventing remote sensors from taking part in the tracking operation. It diminishes redundant information by identifying overlapping sensors; whereas DELTA builds a distributive algorithm to track a target moving at constant speed by dynamically forming a cluster and selecting the CH to reliably monitor moving targets based on light measurement.
While DELTA main drawback stems from the fact that it does not consider varying target speed, the tree- based and cluster-based methods suffer from the fact that the sensing task is usually performed by several nodes at a time. This causes heavy computation on the root node, for the tree-based schemes, and on the CH, for the others. It also makes the tree- or cluster-based WSN tracking systems lack of robustness in the case of root and CH failures.
2.2.2. Prediction-Based Approaches
In recent years many target tracking protocols have been proposed to provide prediction-based methods, where the next position of the target is predicted. The authors in [24] proposed a prediction-based energy aware scheme, referred to as PES. PES built three components: a) a prediction model that is able to help selecting the sensor nodes that are expected to take in charge the tracking; b) a heuristic-based mechanisms that decides which sensor should be activated and when; and c) a recovery mechanism that can be triggered when a tracking disconnection is experienced. Since energy is considered to be the most critical resource, PES assumes that a sensor node remains in a sleeping state as long as possible.
In [13] an algorithm called Dual prediction-based reporting (DPR) was developed. It aimed at reducing the energy needed by the WSN by keeping the sensor in a sleeping mode most of the time and requesting that the computation of target position is performed locally at the sensor nodes and globally at the sink node. Transmissions of sensor messages are escaped as long as the predictions are consistent with each other. DPR achieves energy efficiency by judiciously trading off multi-hop transmissions of the messages between sensors and the sink node.
In [14] , an energy efficient prediction-based algorithm was proposed assuming that the moves of the targets are predictable. The algorithms attempts simply to reduce the transmission distance between the communicating nodes and the number of messages to transmit. The main idea in this algorithm is to use a tri-lateration algorithm, carried out locally by the sensors, for the localization of a target. This makes the cluster head not involved in the needed communications, and thus reduces the energy consumption.
Other target tracking schemes have assumed that the sensor nodes are mobile and the sensing coverage is not full. The main idea in these schemes is to predict the future position of the target and select one among the sensor nodes close to that position and order it to move closer to it. In particular, the authors in [25] proposed a tracking framework based on Voronoi tessellations. A mobility model was proposed to control the coverage degree according to the target presence. The objective is to establish a non-uniform coverage within the monitored zone to allow detecting the target by multiple sensor nodes. Moreover, the authors introduced an algorithm to discover overlapping nodes without providing additional communication cost. This algorithm was shown to be effective in reducing the energy consumption.
3. Target Tracking under Surveillance System
We discuss in this section special requirements of the surveillance process in terms of tracking efficiency and task scheduling.
3.1. Requirements for Efficient Surveillance
WSN-based surveillance applications features are characterized by the nature of the environment where the applications take place and the degree of the tracking efficiency required for the applications. In the following, we discuss the most important WSN characteristics needed to achieve efficient mobile target tracking in a hazardous environment. Some of these characteristics have been discussed in [10] and [6] .
Communication infrastructure: as mentioned before, two common types of WSN communication models are currently used to achieve surveillance: the hierarchical and the flat networks. While the first structure allows the existence of nodes, called cluster heads, capable of performing sophisticated operations and having more energy than simple sensor nodes, the nodes in the flat structure have the same capabilities and should collaborate to relay any report from the generating node to the sink node. In both models, surveillance should be able to optimize the energy consumption and keep connectivity. While hierarchical infrastructures should reduce the relaying activity within clusters, the flat architecture should reduce the number of sensors involved in event collection and target tracking.
Deployments cheme: The deployment of sensor nodes in a surveillance application in an irregular environment cannot be accomplished according to a deterministic choice. Due to the hostility of the physical environment, direct human control of the sensor nodes serving the surveillance application may be hard to achieve, and might be impossible in certain situations. Typically, sensor nodes are dropped from manned/unmanned aircrafts in a given area and should provide total sensing coverage, in some sense. Therefore, a control mechanism should be attached to the deployment scheme to allow measuring the required level of coverage any time. The control may use a large set of parameters that can be effectively monitored, including node density, sensor range, and k-coverage capability.
Energy management: The energy resources of a sensor node are limited because of the sensor size and cost constraints. In fact, localization, sensing functions, and communication techniques could not be performed without taking into consideration energy constraints. In addition, high-resolution information about the monitored area is often needed, requiring the use of energy-aware techniques. Energy is the most important factor occurring in the determination of the WSN lifetime. The required lifetime in the surveillance context should last as long as possible. Therefore, the sensors should be able to be automatically recharged after their amount of energy is consumed, or they should be replaced upon energy depletion or failure. Moreover, to provide surveillance continuity, the system should be able to estimate energy consumption for every sensor and determine in advance the energy failure moment to provide sensor replacement.
Mobile target tracking: Three major requirements have to be fulfilled by sensors in a surveillance system: First, the sensors should be unnoticeable, meaning that their positions should be hard to determine by non-autho- rized parties and their size should be limited. Second, the sensor nodes should be able to locate targets moving under a reasonable speed v in the monitored area (generally, ). Third, the sensor nodes should be able to collaborate with each other to construct the path followed by a target and predict its exit zone from the monitored area.
). Third, the sensor nodes should be able to collaborate with each other to construct the path followed by a target and predict its exit zone from the monitored area.
Monitored area coverage: The sensor nodes in a surveillance application should collaborate to achieve sensing coverage of the whole area in order to collect useful events when they occur and to build continuously the path followed by any target trying to cross the area. In addition, the WSN needs to be connected so that any collected event or target related information is forwarded to the sink node, via the other nodes if needed. Since the communication coverage of a single sensor node is basically dependent on the sensing range of the sensors attached to it, the communication requirements of the surveillance system should depend heavily on the sensor sensitivity to track targets. The WSN must be able to minimize the errors related to mobile target detection and feature measurements.
3.2. Deployment/Scheduling Objectives for Energy-Aware Surveillance
The deployment of sensors for border surveillance may be made in a strip along the borderline of a country with a width sufficiently large. The system should be able to track mobile targets (including individuals, animals, and vehicles), help following their paths, and estimate their exit points from the strip. To this end, the deployment schemes and scheduling activity of the WSN may need comply with two categories of rules: the density controlling rules and the scheduling rules. In the following, we discuss some of these rules.
Density related requirements. It is obvious that the quality of target detection and tracking depends on the number of deployed sensors and the surface of the given strip. An efficient deployment scheme should guarantee that every point in the strip, where a target can be, is sensed by at least one active sensor. However, knowing that the target enters the strip from one edge of the strip and exits it from the other edge, this condition can be achieved by the following rules:
Monitoring line rule: At least one sensing line should be active to detect the beginning of a crossing action. The sensing line is nothing but a sequence of sensors separated by at most twice the sensing range of the sensors. This line should be parallel (in some sense) to the borderline so that an object crossing the strip should traverse it. Furthermore, to provide premature detection, the sensing line should be close to the borderline. The number
of sensors that form the sensing line should be higher than , where
, where  is the sensing range of the sensors and L is the length of the borderline. Most of the time the sensing line is physically a broken line requiring many more sensors than
is the sensing range of the sensors and L is the length of the borderline. Most of the time the sensing line is physically a broken line requiring many more sensors than .
.
Density rule: More generally, if the coverage of every point in the strip is required, the number should be higher than

where W is the width of the strip. The formula assumes that the strip is bounded with a surface equal  and that any sensor, except those on the border of the strip, has at least 6 sensor neighbors (i.e., the traditional pavement in cellular networks). This rule guarantees he high probability that every point in the strip is covered by a sensor, provided that the deployment is uniform.
and that any sensor, except those on the border of the strip, has at least 6 sensor neighbors (i.e., the traditional pavement in cellular networks). This rule guarantees he high probability that every point in the strip is covered by a sensor, provided that the deployment is uniform.
Scheduling constraints. It can be easily seen that the scheduling scheme within surveillance systems should be able to comply with two contradictory objectives. They are the sensor lifetime and the sensing continuity. Three rules can be distinguished.
Lifetime rule: The lifetime of the sensors should be as long as possible, assuming that the energy consumption should be reduced for all sensors and that any target crossing should be detected. This means that the scheduling operation should handle sensor sleeping, target detection, and target tracking tasks with different strategies. The first sensors in charge of target detection should belong to at least one established line of surveillance, for instance; and in that case, the line should be maintained to provide energy reduction and modified from time to time. On the other hand, sensors in charge of tracking must be awakened only when needed.
Prediction Awake rule: Sensors in charge of tracking are awakened when the detected target occurs in their vicinity. Awake sensors in charge of tracking an active target should collaborate to predict the next positions (in the next time slot) of the detected target and reduce the number of the sensors to wake up upon target detection. The prediction of the next positions should be able to help determining which sensor(s) to wake up in the next time slot. Position prediction must take into consideration the geographic nature of the monitored area and the history of target motion.
Tracking continuity rule. Only a few sensors should be awakened to provide continuous target tracking so that targets can be monitored properly (at any time slot) until exit time. Since the time is slotted, we assume here that continuous tracking means that the surveillance system is able to locate the target at any time slot after its/his first detection. Let us notice, however, that this definition can be reduced by changing the expression “any time slot” by the expression “every n time slots”, for small values of n.
4. Border Cooperative Predictive Tracking Scheme
For the sake of simplicity, we suppose in this section that a WSN-based surveillance system is deployed uniformly in a thick strip along a country border, or randomly deployed with a mathematical control such as in [24] , where sensing and radio coverage of the strip were provided. We also assume that a target is crossing the area following an unknown path. Our objective in this section is to construct a tracking scheme, referred to as the Border Cooperative Predictive Tracking (BCPT) scheme. The scheme is a three-step process. In the first step, the target is detected as soon as it enters the strip. In the second step, BCPT wakes up appropriate sensors to follow the crossing target while predicting its next positions. In the final step, it estimates the exit time and exit points (or segment).
The first step can be achieved assuming that a line of active sensors is configured along (and close to) the border. As soon as the target arrives to cross the line, a sensor detects it. The detection can be certainly achieved if the distance between two successive sensors in the line is smaller that , where ε is a positive number commensurate with the maximum speed of the target and the way the sensor performs its function.
, where ε is a positive number commensurate with the maximum speed of the target and the way the sensor performs its function.
The second step is iterative. A sensor s detecting a target at time slot  determines the positions of the target at the following time slots
determines the positions of the target at the following time slots  until it leaves its sensing area. Let
until it leaves its sensing area. Let  be all the positions of the target observed by sensor s at the following time slots. The number n of these positions is obviously finite and depends on the path of the target, since the latter moves to the exit edge of the strip.
be all the positions of the target observed by sensor s at the following time slots. The number n of these positions is obviously finite and depends on the path of the target, since the latter moves to the exit edge of the strip.
Let  be the position of sensor s. At the beginning of time slot
be the position of sensor s. At the beginning of time slot , sensor s estimates the next position
, sensor s estimates the next position , builds a message containing the type of the detected target (or its features, as collected), the two last observed positions (if any), the new position, and the time duration of observation, say
, builds a message containing the type of the detected target (or its features, as collected), the two last observed positions (if any), the new position, and the time duration of observation, say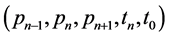 . Then, it sends the message to the sink node and to its neighbors located, out of its tracking range, in the sector centered on
. Then, it sends the message to the sink node and to its neighbors located, out of its tracking range, in the sector centered on , using segment
, using segment ![]() as an axis, and having an angle
as an axis, and having an angle ![]() and a radius R given respectively by:
and a radius R given respectively by:
![]() ,
,
![]()
where ![]() is the angle formed by segments
is the angle formed by segments ![]() and
and![]() , L is a constant appropriately selected, and
, L is a constant appropriately selected, and ![]() is a threshold. Let
is a threshold. Let ![]() be this zone. The transmitted message is written as:
be this zone. The transmitted message is written as:
![]()
Figure 1 depicts the sector where, sensor neighbors should be able to receive the message. We call this process the L-wakeup process.
When ![]() and
and ![]() belong to the same line (i.e.,
belong to the same line (i.e.,![]() ), the value of
), the value of ![]() allows
allows ![]() to be positive.
to be positive. ![]() can be determined based on the duration of the time slot, the motion of the target, and the density of sensors. In particular, if the WSN deployment scheme is known, the value of
can be determined based on the duration of the time slot, the motion of the target, and the density of sensors. In particular, if the WSN deployment scheme is known, the value of ![]() can be selected so that the aforementioned sector contains at least one sensor out of the range of sensor s that is able to cover the expected position
can be selected so that the aforementioned sector contains at least one sensor out of the range of sensor s that is able to cover the expected position![]() of the target (Figure 1). The sensor receives the message, wakes up, and starts tracking the target from position
of the target (Figure 1). The sensor receives the message, wakes up, and starts tracking the target from position![]() .
.
Distance ![]() depicted in Figure 1 should be lower than the sensing range of the sensors so that a sensor can be found in the area of the sector outside the sensing disk centered in
depicted in Figure 1 should be lower than the sensing range of the sensors so that a sensor can be found in the area of the sector outside the sensing disk centered in![]() , if sensing continuity is needed.
, if sensing continuity is needed.
If the sink node receives a messages from sensors ![]() followed by a second message from
followed by a second message from ![]() related to the same target as denoted by:
related to the same target as denoted by:
![]()
and reporting on the positions of the target![]() , and
, and ![]() for
for![]() , it runs the following procedures
, it runs the following procedures
Positions’ correlation: if the reported positions correspond to the same time slots then these position are compared. If they are different, then a new position is computed to replace the reported position (as the middle of these positions, for example) and the predicted position are revisited.
Dropping messages: the receiving sensor, say![]() , of message
, of message ![]() and
and ![]() can easily deduce, if
can easily deduce, if
![]() ,
,
![]()
Figure 1. Wake up zone after prediction.
that sensor ![]() is reporting on a target already under tracking. Sensor
is reporting on a target already under tracking. Sensor ![]() drops message
drops message ![]() and keeps following the target. Meanwhile, upon receiving the messages generated by the detecting sensors, the sink node should be able to estimate the time spent by the target, under each sensor, while moving through its path until the current time slot (say
and keeps following the target. Meanwhile, upon receiving the messages generated by the detecting sensors, the sink node should be able to estimate the time spent by the target, under each sensor, while moving through its path until the current time slot (say![]() ) and the zone where the target is likely to be at next time slot
) and the zone where the target is likely to be at next time slot![]() .
.
Let us now discuss some important features of the cooperative predictive tracking scheme. In particular, let us study the tracking continuity property of the scheme. Establishing this property requires three major constraints; namely, the sensor sensing continuity, the sensing granularity, and the target path visibility. Sensor sensing continuity assumes that every awake sensor senses its area at least once per time slot. This constraint can be reduced by requesting that the sensor should sense every m time slots (![]() ). A good value of m can be made with respect to the maximum speed
). A good value of m can be made with respect to the maximum speed ![]() of the target and the number of detected positions when crossing the area. Sensing granularity states that the target cannot move
of the target and the number of detected positions when crossing the area. Sensing granularity states that the target cannot move ![]() meters without being sensed by a sensor. This shows that the speed of the target per time should be lower than
meters without being sensed by a sensor. This shows that the speed of the target per time should be lower than![]() .
.
Finally, Target path visibility constraint assumes that, if the crossing time is larger than n time slots, then the path followed by the tracked target includes more than n detected positions. This assumption guarantees that, if the time passed by a target to cross the area monitored by a sensor s is longer than a time slot, then the sensor will detect the target more than once. More generally, if the target spends more than m slots to cross the area controlled by s, then it will be detected at least m times.
The following result shows that the tracking continuity property can be achieved when the target mobility and sensing range cope with the strip width, the place of the surveillance line, and the time slot duration. The result involves a discussion on the angle ![]() of the wake up zone and the distance
of the wake up zone and the distance![]() , where
, where ![]() is a quantity commensurate with the speed of target.
is a quantity commensurate with the speed of target.
Proposition 1 (tracking continuity). Assume a target is crossing the border strip with a speed ![]() measured in meters per time slot. The continuity of target tracking can be guaranteed using the -wakeup process provided that the following statements hold:
measured in meters per time slot. The continuity of target tracking can be guaranteed using the -wakeup process provided that the following statements hold:
1) The quantity ![]() is selected in such a way that the speed of the target is lower than
is selected in such a way that the speed of the target is lower than![]() .
.
2) The width and angle ![]() are selected in such a way that
are selected in such a way that ![]() contains sensor for all sensors. This shows that:
contains sensor for all sensors. This shows that:
・ the deployment density is higher than![]() .
.
・ The width L, angle![]() , and the diagonal
, and the diagonal ![]() of the wake up zone
of the wake up zone ![]() verify the following inequalities:
verify the following inequalities:
![]() .
.
![]() .
.
Proof.
The first condition states that the target should be detected by one sensor on the active thick line (barrier) characterized by a certain width w. Figure 2 depicts such a thick line. If the distance between two neighbors in that line is lower than![]() , then a simple computation shows that
, then a simple computation shows that
![]()
Since an active sensor senses once in a time slot, the target speed should not exceed 2w. Therefore, ![]() should be selected so that
should be selected so that![]() .
.
One can see that once a target is detected, the detecting sensor, say s, follows it until it gets out of its sensing area![]() . The continuity is guaranteed if the sensor is able to find another neighboring sensor to take in charge the tracking until the target gets out of its range. In that case the sensor should find another and so on. The second condition guarantees the existence of a sensor, in the part of the sector external to sensing area the sensing area of a sensor informing its neighbors that the target is leaving its area, is related to the density of sensor in the strip. In fact, the area of the external region
. The continuity is guaranteed if the sensor is able to find another neighboring sensor to take in charge the tracking until the target gets out of its range. In that case the sensor should find another and so on. The second condition guarantees the existence of a sensor, in the part of the sector external to sensing area the sensing area of a sensor informing its neighbors that the target is leaving its area, is related to the density of sensor in the strip. In fact, the area of the external region ![]() occurring in the sector outside the range of the detecting sensor s is equal to:
occurring in the sector outside the range of the detecting sensor s is equal to:
![]()
where ![]() is the defined angle of the sector. The fact that the density is higher than
is the defined angle of the sector. The fact that the density is higher than![]() , shows that at least one sensor occurs in the zone
, shows that at least one sensor occurs in the zone![]() .
.
Finally, the last inequality guarantees that the diagonal ![]() of the external part of the sector centered in
of the external part of the sector centered in ![]() is lower than
is lower than![]() . Using Figure 1, one can show that diagonal
. Using Figure 1, one can show that diagonal ![]() is equal to
is equal to
![]()
The third condition implies that to provide detection of the target by a sensor in![]() , the distance between points A and B should lower than
, the distance between points A and B should lower than ![]() in addition to
in addition to![]() . The distance between A and B is clearly given by
. The distance between A and B is clearly given by![]() .
.
Hence, we deduce that the WSN is able to construct the target path, from the moment it is detected until the moment it leaves the strip, provided that the two conditions of the theorem are satisfied. ![]()
Let us inform that the second condition in the theorem imposes a constraint on![]() . For the sake of simplicity, we do not compute this bound of
. For the sake of simplicity, we do not compute this bound of![]() ; but, we notice that
; but, we notice that ![]() should be smaller than π/6. When the deployment is not deterministic, the second condition cannot be established, since
should be smaller than π/6. When the deployment is not deterministic, the second condition cannot be established, since ![]() may not contain a sensor, even when
may not contain a sensor, even when![]() . Section 6 will address this situation.
. Section 6 will address this situation.
5. Predicting Target Exit
In this section, we first develop a mobility model for a generic target crossing the strip. Then we establish the major features of our prediction scheme based on this model. Finally, we describe how our algorithm predicts the exit time and exit zone of the target.
5.1. Target Modeling and Assumptions
To be detected, the target should move at a speed (counted in meters per time slot) higher than a given minimum speed ![]() and lower than a given maximum speed
and lower than a given maximum speed![]() , depending on the characteristics of the detecting sensors. The following rules, called target mobility rules and target path rules, define how the target moves towards the exit edge of the border strip under uncontrolled or controlled time mode.
, depending on the characteristics of the detecting sensors. The following rules, called target mobility rules and target path rules, define how the target moves towards the exit edge of the border strip under uncontrolled or controlled time mode.
Target mobility rules. Assuming that the target is at position p at time slot t, a mobility rule supposes that the new position ![]() of the target at the following time slot
of the target at the following time slot ![]() is randomly located in a sector zone centered in p, at a distance d from p and an angle
is randomly located in a sector zone centered in p, at a distance d from p and an angle ![]() with respect to the borderline randomly selected in interval
with respect to the borderline randomly selected in interval ![]() and
and![]() , respectively, assuming that
, respectively, assuming that ![]() and
and![]() . Figure 3 depicts the mo-
. Figure 3 depicts the mo-
bility rule of the target. The angle ![]() characterizes the maximal deviation with respect to the shortest exit direction. Indeed,
characterizes the maximal deviation with respect to the shortest exit direction. Indeed, ![]() ensures that the target is moving towards of the exit edge of the strip.
ensures that the target is moving towards of the exit edge of the strip.
The distances ![]() and
and ![]() correspond to the minimal speed
correspond to the minimal speed ![]() and the maximal speed
and the maximal speed ![]() of the target during one time slot. It is obvious that
of the target during one time slot. It is obvious that ![]() should be strictly positive and that
should be strictly positive and that ![]() should be commensurate
should be commensurate
with sensing range, the sensor sensitivity, and the slot duration. In particular, when ![]() is very large, the border surveillance system may not be able to detect the target. Moreover, if
is very large, the border surveillance system may not be able to detect the target. Moreover, if![]() , the target can keep moving parallel to the borderline without getting out from the strip. Finally, if
, the target can keep moving parallel to the borderline without getting out from the strip. Finally, if![]() , the target may spend a quasi-infinite time to exit the strip.
, the target may spend a quasi-infinite time to exit the strip.
Target path rules: Several rules can be reasonably used to model the target path. A first rule assumes that the target approaches the exit edge of the strip with at least ![]() meters at every time slot (or a given number of slots). The minimum value of displacement
meters at every time slot (or a given number of slots). The minimum value of displacement ![]() may be determined in function of the maximal deviation
may be determined in function of the maximal deviation
![]() and the minimal target velocity
and the minimal target velocity ![]() using the following formula
using the following formula
![]()
This rule states again that ![]() and that the maximum time
and that the maximum time ![]() that the target may spend to reach the exit edge of the strip is given by
that the target may spend to reach the exit edge of the strip is given by
![]()
where ![]() is the distance of the initial place
is the distance of the initial place ![]() to the exit edge and
to the exit edge and ![]() is the floor function. Since the target motion towards the exit edge depends on the nature of the strip (e.g., including vegetation, obstacles, and geographic diversity), our target model allows the distance d made by the target in one time slot to be randomly selected to help representing the strip nature effects on the target path. Modeling the path followed by a target during n time slots starting from time slot
is the floor function. Since the target motion towards the exit edge depends on the nature of the strip (e.g., including vegetation, obstacles, and geographic diversity), our target model allows the distance d made by the target in one time slot to be randomly selected to help representing the strip nature effects on the target path. Modeling the path followed by a target during n time slots starting from time slot ![]() can be done by a sequence
can be done by a sequence ![]() defined by
defined by
![]()
where n is the number of time slots used to observe the target, ![]() is the identity of the sensor observing the target at the kth slot,
is the identity of the sensor observing the target at the kth slot, ![]() is the position of sensor
is the position of sensor![]() , and
, and ![]() is the (angular) position of the target observed at the kth slot with respect to
is the (angular) position of the target observed at the kth slot with respect to![]() .
.
Let ![]() be the distance between
be the distance between ![]() and
and![]() , one can easily deduce that, if
, one can easily deduce that, if ![]() measures the distance between
measures the distance between ![]() and the exit edge, the following relations hold
and the exit edge, the following relations hold
![]()
and
![]()
since ![]() for all
for all![]() . Therefore, we can deduce that the series
. Therefore, we can deduce that the series ![]() is decreasing. It stops when
is decreasing. It stops when ![]() becomes lower than
becomes lower than![]() .
.
Thus, we have the following result.
Proposition 2. Assume that the aim of a target is to reach the exit edge of the border strip and that the monitoring line active has detected him/it at time slot ![]() and that the density rule, the mobility rule and target path rule are satisfied. Then, the following statements stand:
and that the density rule, the mobility rule and target path rule are satisfied. Then, the following statements stand:
1) The path modeling process converges in a finite time, meaning that the target will reach the exit edge in a time shorter than a maximum time given by
![]()
2) The maximum length l of the path followed by the target between its detection point and time termination is given by
![]()
Proof.
The process has been shown to terminate by providing the computation of the maximum time to reach the exit edge![]() , provided that the motion of the target is governed by the mobility rule. One can easily see that at every time slot after
, provided that the motion of the target is governed by the mobility rule. One can easily see that at every time slot after ![]() (i.e., after a first detection is performed), the next position of the target is closer to the exit edge of the strip, provided that the mobility rule is satisfied. The process terminates when the sensing disk of the detecting sensor overlaps the exit edge of the strip and that expected next position is out of strip. This means that the process stops at the
(i.e., after a first detection is performed), the next position of the target is closer to the exit edge of the strip, provided that the mobility rule is satisfied. The process terminates when the sensing disk of the detecting sensor overlaps the exit edge of the strip and that expected next position is out of strip. This means that the process stops at the ![]() slot when
slot when
![]()
Computing the length of the target path travelled until time slot k is given by![]() . This length is bounded as follows
. This length is bounded as follows
![]()
The inequalities can be easily stated using the mobility and target path rules, knowing that![]() , for all j.
, for all j. ![]()
5.2. Prediction Features
Let us now study the sequence ![]() defined by
defined by![]() , as obtained by the mobility model after a target is detected, and let us update it at any slot where a new observation of the target is made by a sensor. The objectives here are to maintain the modeled path of crossing target and to estimate his/its exit time and exit place efficiently. Let us first summarize the technique we use to achieve this. The technique is iterative and maintains three variables as time slots go; namely, the current position
, as obtained by the mobility model after a target is detected, and let us update it at any slot where a new observation of the target is made by a sensor. The objectives here are to maintain the modeled path of crossing target and to estimate his/its exit time and exit place efficiently. Let us first summarize the technique we use to achieve this. The technique is iterative and maintains three variables as time slots go; namely, the current position![]() , the next positions
, the next positions![]() , of the target, the expected zone of exit (i.e. a segment
, of the target, the expected zone of exit (i.e. a segment ![]() on the exit edge), and the expected time of exit
on the exit edge), and the expected time of exit![]() .
.
During step n, the predicted position of the target is replaced by the observed position![]() . This process helps selecting the next sensor that will insure the tracking continuity in the time slot
. This process helps selecting the next sensor that will insure the tracking continuity in the time slot ![]() and delimiting the exit segment. Once selected, this sensor updates the predicted position of the target according to its observation. Then, the next positions, in the
and delimiting the exit segment. Once selected, this sensor updates the predicted position of the target according to its observation. Then, the next positions, in the ![]() time slot,
time slot, ![]() , of the target knowing its position
, of the target knowing its position ![]() are approximated using the mobility model presented in the above subsection,
are approximated using the mobility model presented in the above subsection,
Let us now show how the sink node predicts the exit time of a target along with its exit segment, as it is kept informed by the target motion. To this end, we consider the following notations: Let ![]() be the sensing disc of a sensor s tracking the target at the
be the sensing disc of a sensor s tracking the target at the ![]() time slot. Let
time slot. Let ![]() be the diameter of this disc parallel to the exit edge of the strip, and
be the diameter of this disc parallel to the exit edge of the strip, and ![]() be the projection of
be the projection of ![]() on the exit edge. We refer to the resulting segment
on the exit edge. We refer to the resulting segment ![]() as the potential exit segment of the target at time n. Finally, let
as the potential exit segment of the target at time n. Finally, let ![]() be the segment on the exit edge delimited by the intersections between the edge and the two possible lines drawn from the expected position
be the segment on the exit edge delimited by the intersections between the edge and the two possible lines drawn from the expected position ![]() and forming an angle
and forming an angle ![]() with the exit edge. We refer to the segment
with the exit edge. We refer to the segment ![]() as the exit segment of target at the
as the exit segment of target at the ![]() time slot. Figure 4 depicts these segments to clarify the notations.
time slot. Figure 4 depicts these segments to clarify the notations.
Let us compute the different segment using ![]() and the distance
and the distance![]() . If
. If ![]() and
and![]() , we have:
, we have:
・ ![]()
・ ![]()
・ ![]()
・ ![]()
・ ![]()
・ ![]()
where ![]() half of the length of segment
half of the length of segment![]() . It is simply given by:
. It is simply given by:
![]()
The following result studies the evolution of the potential exit time and exit segment of the target, assuming that the distance separating the target from the exit edge decreases of at least ![]() meters every time slots, as a result of the mobility model. A similar result can be obtained if the assumption is replaced by the following weaker one: the distance separating the target from the exit edge decreases of at least
meters every time slots, as a result of the mobility model. A similar result can be obtained if the assumption is replaced by the following weaker one: the distance separating the target from the exit edge decreases of at least ![]() meters every timeslots (
meters every timeslots (![]() ).
).
Proposition 3. a target crossing the border strip and ![]() and
and ![]() be the series of potential exit segments and exit segments, respectively. Then, the following statements hold, provided that the target follows the target mobility rule:
be the series of potential exit segments and exit segments, respectively. Then, the following statements hold, provided that the target follows the target mobility rule:
1) The length ![]() of segment
of segment ![]() satisfies the inequality for all k:
satisfies the inequality for all k:
![]()
2) The two sequences ![]() and
and ![]() are finite and converge to the same segment limit, which is
are finite and converge to the same segment limit, which is ![]() length.
length.
3) If position ![]() is attained by the target at time slot n, then the target will reach the exit edge at a time
is attained by the target at time slot n, then the target will reach the exit edge at a time![]() , where
, where
![]()
![]()
Figure 4. Example of potential exit segments.
![]()
Proof.
First, let us notice that using the mobility rule we can show that the inclusion ![]() holds and the sequence
holds and the sequence ![]() is strictly decreasing. Let us now prove the equality
is strictly decreasing. Let us now prove the equality
![]()
Figure 5 depicts the segments ![]() and
and![]() . One can see that the function:
. One can see that the function:
![]()
This function is continuous. Let ![]() an angular representation of
an angular representation of![]() . For a given
. For a given![]() , the function reaches its minimum for
, the function reaches its minimum for ![]() or
or ![]() (points a et
(points a et ![]() in Figure 5). It reaches its maximum at
in Figure 5). It reaches its maximum at ![]() (points b in Figure 5). This shows that:
(points b in Figure 5). This shows that:
![]()
where:
![]() and
and ![]()
Second, one can deduce from the first statement that ![]() is strictly decreasing and that
is strictly decreasing and that
![]()
The two series are finite since at every step the target approaches the edge by at least ![]() meters (and by at most
meters (and by at most ![]() meters) each time slot and that the tracking process stops when a sensor close to the exit edge wakes up to track the target. The distance of this sensor to the exit edge is therefore smaller than
meters) each time slot and that the tracking process stops when a sensor close to the exit edge wakes up to track the target. The distance of this sensor to the exit edge is therefore smaller than![]() .
.
The number of elements in these series is thus lower than ![]() as stated by Proposition 2.
as stated by Proposition 2.
Third, it has been shown in Subsection 5.1 that if the target is detected at a position p then it reaches the edge before a maximum time ![]() given by:
given by:
![]()
One can also easily show that the target will arrive after a time ![]()
![]()
Applying these inequalities, when![]() , gives the following: if the target it position
, gives the following: if the target it position ![]() at the time slot
at the time slot![]() , then the target will reach the edge at a time
, then the target will reach the edge at a time![]() , where:
, where:
![]()
![]()
Various methods can be utilized to estimate the time of exist. One could estimate![]() , set at time slot k, by
, set at time slot k, by
![]()
Another method computes the average distance per slot travelled by the target and set, at time slot k, an estimation of the exit time by:
![]()
6. An ad hoc Deployment for Target Tracking
Without loss of generality, we assume in this section that the strip to monitor along the country border is a rectangle of length L and width W positioned between points![]() , and
, and![]() . We also assume that
. We also assume that![]() . Our deployment scheme, referred to as BCTP, operates as follows: The dropping of the WSN is operated by a quadcopter flying at an altitude h (generally varying from 70 to 150 meters) and along the lines of equations
. Our deployment scheme, referred to as BCTP, operates as follows: The dropping of the WSN is operated by a quadcopter flying at an altitude h (generally varying from 70 to 150 meters) and along the lines of equations
![]()
On each line the quadcopter is assumed to drop a sensor at each instant ![]() where
where ![]() is the in-
is the in-
stant when the quadcopter is at point![]() . The dropping points are given by
. The dropping points are given by
![]()
Taking into consideration the environment conditions of dropping and assuming that the quadcopter keeps a constant speed equal to V meters per second, one can state that the landing point of a sensor dropped at time ![]() is given by [24] as:
is given by [24] as:
![]()
where ![]() and
and ![]() are wind forces on axis x and axis y, m is the mass of the dropped sensor, and are and the universal acceleration. The dropping and landing processes are depicted in Figure 6. If
are wind forces on axis x and axis y, m is the mass of the dropped sensor, and are and the universal acceleration. The dropping and landing processes are depicted in Figure 6. If![]() , then the landing point
, then the landing point ![]() is given by
is given by
![]()
In the following we assume that![]() ,
, ![]() and
and ![]() One can deduce easily that the possible landing points of a sensor dropped at time
One can deduce easily that the possible landing points of a sensor dropped at time ![]() is a rectangle
is a rectangle ![]() centered in
centered in![]() with a length and width equal to
with a length and width equal to ![]() and
and![]() , respectively.
, respectively.
Theorem 4. Let ![]() be a target crossing the border strip where a WSN is deployed under BCPT. Assume the target speed per time slot belong to
be a target crossing the border strip where a WSN is deployed under BCPT. Assume the target speed per time slot belong to![]() . Then, using the
. Then, using the ![]() -wakeup process, the continuous tracking holds provided that:
-wakeup process, the continuous tracking holds provided that:
・ ![]() ;
;
・ ![]() and
and
・ ![]()
Proof.
First, let us notice that all the rectangles around ![]() have the same dimensions and that, together, they form a thick line of width
have the same dimensions and that, together, they form a thick line of width![]() , if
, if
![]()
This inequality states that ![]() and
and ![]() should intersect. Since tracking continuity means, first, that all point in that all points in the first thick line
should intersect. Since tracking continuity means, first, that all point in that all points in the first thick line ![]() are covered. This is obviously achieved when the diagonal of each rectangle is lower than
are covered. This is obviously achieved when the diagonal of each rectangle is lower than![]() . Therefore we should have:
. Therefore we should have:
![]()
Second, continuity imposes that the speed of the target ![]() should lower the width of the first thick line w. This condition is realized if
should lower the width of the first thick line w. This condition is realized if
![]()
Finally, let s be a sensor tracking the target and that at time slot n, sensor realizes that the target is in position p and that it will be in a position p’ out of its tracking range. Let us consider the zone ![]() for
for
![]() and denote it by
and denote it by![]() . We should demonstrate that, if
. We should demonstrate that, if ![]() then
then ![]()
contains a sensor. An easy computation shows that under this condition, ![]() contains a rectangle among those containing the deployed sensors.
contains a rectangle among those containing the deployed sensors. ![]()
More generally, for given![]() , and
, and ![]() and applying the L-wakeup process, for
and applying the L-wakeup process, for![]() , one cannot guarantee tracking continuity, but can compute the probability that the first line guarantees the detection of target and the probability that
, one cannot guarantee tracking continuity, but can compute the probability that the first line guarantees the detection of target and the probability that ![]() contains a sensor, knowing that BCPT deploys uniformly the sensors in the related rectangle. Then one can deduce the probability that the continuity of target tracking is true in the monitored area.
contains a sensor, knowing that BCPT deploys uniformly the sensors in the related rectangle. Then one can deduce the probability that the continuity of target tracking is true in the monitored area.
7. Performance Evaluation
In this section, we present the results of the simulations we have conducted. The aim of these simulations was to evaluate the performance of the target tracking method we proposed to show its efficiency, in terms of energy consumption and the exit time and zone estimation. We also evaluate respectively the scheduling messages overhead, the deployment coverage in terms of tracking continuity, and the network lifetime.
7.1. The Simulation Model
The simulation model is built by considering that the area to be monitored is of size ![]() meters and that it is partitioned into
meters and that it is partitioned into ![]() of squares of 25 meters side. A set of sensors of size
of squares of 25 meters side. A set of sensors of size ![]() is deployed uniformly in that strip (one in each square). The sensors are assumed to have the same sensing range
is deployed uniformly in that strip (one in each square). The sensors are assumed to have the same sensing range ![]() varying in the set
varying in the set ![]() and that
and that ![]() is wider than π/12. The communication range on the sensors equal to
is wider than π/12. The communication range on the sensors equal to![]() . In the following numerical experiments we will discuss the impact of the sensing range
. In the following numerical experiments we will discuss the impact of the sensing range![]() , the targets’ arrival law, the angle
, the targets’ arrival law, the angle![]() , and the size of (or target speed) on the performance of the surveillance coverage and its ener-
, and the size of (or target speed) on the performance of the surveillance coverage and its ener-
gy consumption. For this, we will conduct simulations by varying ![]() in the above set,
in the above set, ![]() in
in![]() , and
, and ![]() in {5,10,15}. Targets will be assumed to arrive uniformly in time and space.
in {5,10,15}. Targets will be assumed to arrive uniformly in time and space.
Three major objectives will be studied in the sequel. First, the quality of coverage (including the barrier) will be discussed. Second, the discontinuity ratio will be analyzed as a function of important factors including![]() , and
, and![]() . Third, the efficiency of our method will be discussed in terms of communication overhead and exit estimation quality. Such studies will help dimensioning the deployment process and the value of
. Third, the efficiency of our method will be discussed in terms of communication overhead and exit estimation quality. Such studies will help dimensioning the deployment process and the value of ![]() to reduce the number of active deployed sensor and guarantee tracking continuity.
to reduce the number of active deployed sensor and guarantee tracking continuity.
7.2. Numerical Experiments
7.2.1. The Deployment Efficiency
Simulations have been conducted to evaluate our deployment scheme and the quality of coverage of the barrier (i.e., the first line of surveillance along the border). The evaluation of the scheme is made by measuring the proportion of uncovered points in the area, while ![]() varies in the set
varies in the set![]() . As mentioned before, the monitored area is assumed to be decomposed into squares of 25 meters side. The aerial deployment is presumed to deploy one sensor in each square. A barrier is built on the sensors deployed in the squares along the border. By discretizing the problem we have reduced it to the problem of checking whether the points of grid is out of the range of the randomly deployed sensors. Figure 7 depicts the evolution of the uncovered set of points and compares it with the absence of coverage, in the case where the sensors are in the middle of the squares.
. As mentioned before, the monitored area is assumed to be decomposed into squares of 25 meters side. The aerial deployment is presumed to deploy one sensor in each square. A barrier is built on the sensors deployed in the squares along the border. By discretizing the problem we have reduced it to the problem of checking whether the points of grid is out of the range of the randomly deployed sensors. Figure 7 depicts the evolution of the uncovered set of points and compares it with the absence of coverage, in the case where the sensors are in the middle of the squares.
One can notice that the loss of coverage for our scheme decreases when the sensing range of the sensors range increases and that all points are covered when ![]() becomes larger than
becomes larger than ![]() (i.e., the square side), while the range is only needed to by higher than
(i.e., the square side), while the range is only needed to by higher than![]() , in the deterministic case.
, in the deterministic case.
Figure 8 depicts the level of barrier coverage for different values of ![]() and
and![]() . It can be seen that when
. It can be seen that when ![]() is large, the full coverage of the barrier of the barrier is reached for larger values of
is large, the full coverage of the barrier of the barrier is reached for larger values of![]() . Obviously, the deterministic case performs slightly better.
. Obviously, the deterministic case performs slightly better.
7.2.2. Tracking Overhead
In a first series of simulations, we evaluate the wake up protocol overhead and measured it through the number
of additional messages due to the proposed scheduling and tracking scheme. For the deployment, we fixed the
sensing range ![]() to 30 meters and considered two values for the angle
to 30 meters and considered two values for the angle![]() ,
, ![]() and
and![]() . We varied the arrival
. We varied the arrival
number x of targets per time slot from 1 to 10 and measured, for each value of the arrival number, the average number of messages generated by the sensors tracking the targets during 500 time slots. In addition, without loss
of generality, we assumed that the trespassers travel through the shortest path or the longest paths (for ![]() and
and![]() ) with a speed equal to 20 meters per time slot.
) with a speed equal to 20 meters per time slot.
The variation of the messages rate is illustrated in Figure 9, where it can be seen that overhead does not ex-
ceed 60 messages for ![]() and 40 messages for
and 40 messages for![]() , respectively, knowing during the simulation period 5000
, respectively, knowing during the simulation period 5000
targets attempt to cross the strip. This can be explained by the fact that a target induces the generation of 10 to 12 messages when, ![]() and 10 to 16 messages
and 10 to 16 messages![]() , respectively.
, respectively.
7.2.3. The Tracking Continuity
The tracking continuity is studied here for width of the wake up zone equal to![]() , assuming that BCPT is utilized and that the sensors are deployed in squares of side length equal to 25 meters. Since the tracking continuity depends on the value of the sensing range
, assuming that BCPT is utilized and that the sensors are deployed in squares of side length equal to 25 meters. Since the tracking continuity depends on the value of the sensing range![]() , the value of angle
, the value of angle![]() , and the angle
, and the angle![]() , we select several values of these parameters and discuss the continuity while comparing it with the continuity features under deterministic deployment. For the latter, we assume that the sensors are placed on the centers of the rectangle.
, we select several values of these parameters and discuss the continuity while comparing it with the continuity features under deterministic deployment. For the latter, we assume that the sensors are placed on the centers of the rectangle.
Finally, we assume that during simulation a large number of targets attempt to cross the strip from random
points on the border, and that these targets follow straight lines with directions varying randomly in ![]() with respect to the border line.
with respect to the border line.
Figure 10 depicts de average distance walked by a target towards the exit edge before a tracking disconnection is observed, knowing that the width of the strip is equal to 125 meters. When ![]() exceeds 3/2 times the
exceeds 3/2 times the
side of the squares where sensors are deployed, the tracking is guaranteed until exit when![]() .
.
7.2.4. The Estimation Efficiency
The final set of experiments discuss the size variation of the exit segment length report for the crossing targets with respect to the sensing range of the sensors and the angle![]() . Figure 11 depicts this variation. One can no-
. Figure 11 depicts this variation. One can no-
tice that, for![]() , the exit segment is too high for small values of
, the exit segment is too high for small values of![]() . This fact is justified by the fact that, when the target in the strip, the possible exit point assumed by the target mobility model belongs to a segment of length
. This fact is justified by the fact that, when the target in the strip, the possible exit point assumed by the target mobility model belongs to a segment of length ![]() meters (about 216 meters). The length of the initial segment is only equal to 125 and 65 meters for
meters (about 216 meters). The length of the initial segment is only equal to 125 and 65 meters for ![]() and
and![]() , respectively.
, respectively.
On the other hand, the segment length is lower than ![]() when
when ![]() gets higher than the square size for the three values of
gets higher than the square size for the three values of![]() . This is due to the fact that for such ranges the target has walked more than half of the width strip.
. This is due to the fact that for such ranges the target has walked more than half of the width strip.
8. Conclusions
Border surveillance systems should comply with very constraining features to be efficient. In particular, they should provide immediate detection of trespassers and guarantee tracking continuity. The system presented in this paper includes various thick lines of surveillance along the country border. It reduced the energy consumption of tracking processes by reducing properly the number of sensors to wake up for tracking. It also provides a prediction technique capable of estimating the exit time and zone of crossing targets.
The results developed within this work can be extended to encompass the security of the monitoring network, sensor fault tolerance, and coverage holes. It also can be extended to various applications such as battlefields and mining.
Acknowledgements
The author is thankful to the Tunisian Ministry for High Teaching and Scientific Research for funding the research presented in this paper.