Abstract

A delayed biological system of predator-prey interaction with stage structure and density dependent juvenile birth rate is investigated. It is assumed that the prey population has two stages: immature and mature. The growth of the immature prey is density dependent and is a function of the density of adult prey. Such phenomenon has been reported for beetles, tribolium, copepods, scorpions, several fish species and even crows. The growth of the predator is affected by the time delay due to gestation. By some Lemmas and methods of delay differential equation, the conditions for the uniform persistence and extinction of the system are obtained. Numerical simulations illustrate the feasibility of the main results and demonstrate that the density dependent coefficient has influence on the system populations’ densities though it has no effect on uniform persistence and extinction of the system.

Keywords

Uniform Persistence, Periodicity, Extinction, Density Dependence, Stage Structure

Share and Cite:

Received 20 May 2016; accepted 17 June 2016; published 20 June 2016

1. Introduction

In the natural world, there are many species whose individual members have a life history that takes them through two stages: juvenile and adult. Individuals in each stage are identical in biological characteristics, and some vital rates (rates of survival, development and recruitment) of individuals in a population almost always depend on stage structure [1] - [3] . Thus, we need to consider stage structure in population problems accordingly. In recent years, some authors ( [1] - [18] ) studied the stage-structured predator-prey systems. The authors of [2] - [11] have studied the stability or Hopf bifurcation of these type systems. Since environmental and biological parameters (such as the seasonal effects of weather, food supplies, mating habits, hunting or harvesting season, etc.) fluctuate naturally over time, the authors of [12] - [18] have explored a class of nonautonomous biological systems with stage structure. Recently, Yang et al. considered the following predator-prey system with stage structure for prey [18] :

(1.1)

All the coefficients in system (1.1) are continuous positive 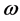periodic functions. Sufficient and necessary conditions are obtained for the permanence of the system.

Sometimes, the past state as well as current conditions can influence biological dynamics and such interactions have motivated the introduction of time delay in stage-structured predator-prey systems [2] - [5] [8] - [13] . Time delay due to gestation is the time interval between the moments when an individual prey is killed and when the corresponding biomass is added to the predator population. That is to say, the reproduction of predator after predating the prey is not instantaneous but will be mediated by some discrete time lag required for gestation of predator. The authors of [8] - [10] have studied a class of stage-structured predator-prey models with time delay due to gestation of predator.

In some stage-structured populations, the intraspecific and interspecific competitions occur within each stage structure. And each stage-structured density affects not only its population but also other stage-structured populations. In two-stage single-species population, Abrams and Quince have demonstrated that adult population competition makes a low birth rate of juvenile population [19] . Adult population has to compete for resources to reproduce when population size or density is larger. Correspondingly, juvenile population birth rate is a function of adults’ density and remains bounded when adults’ size is large due to limited resources [20] . This density- dependent regulator has been found in beetles, tribolium, copepods, scorpions, several fish species and even crows by Polis [21] .

Motivated by the above facts and based on the recent work of Yang et al. [18] , we consider the following stage-structured predator-prey model:

(1.2)

where, and represent the density of immature prey, mature prey and predator species, respectively. The coefficients in system (1.2) are all continuous positive T periodic functions in which represents the maximum per capita birth rate into the immature prey, is the recruitment rate of immature prey becoming mature prey, is the death rate of the immature prey population, and is death rate of the mature prey population. The parameter is the proportional rate of decrease in per capita births with increased mature prey density and takes a value between 0 and 1 [19] , which can be considered as density de-

pendent coefficient. The function represents the Holling type-IV functional re-

sponse of the predator to the immature prey and is the conversion rate of nutrients into the reproduction of the predator. The parameter is the delay due to gestation, that is, only the mature adult predator can contribute to the production of predator biomass. The parameters and denote the death rate and the overcrowding rate of the predator population, respectively.

The initial conditions for system (1.2) take the form of

(1.3)

where, the Banach space of continuous functions mapping the interval

into, where we define and the interior of as

.

At the same time, we adopt the following notations through this paper:

(1.4)

where is a continuous T-periodic function.

The remainder of this paper is organized as follows. In Section 2, we introduce some lemmas and then explore the uniformly persistence and periodicity of system (1.2). In Section 3, we investigate the extinction of the predator population in system (1.2). In Section 4, numerical simulations are presented to illustrate the feasibility of our main results. Conclusion is given in Section 5.

2. Uniform Persistence and Periodicity

In this section, we analyze the uniform persistence and periodicity of system (1.2) with initial conditions (1.3). First, we introduce the following definition and lemmas, which are useful for obtaining our results.

Definition 2.1. The system, is said to be uniformly persistent if there are constants

such that every positive solution of this system satisfies.

Definition 2.2. The system, is said to be weakly uniformly persistent if there are

constants such that every positive solution of this system satisfies.

Lemma 2.1. (See [22] ). If and are all continuous T periodic functions for all, and, then the system

, (2.1)

has a unique positive T periodic solution which is globally asymptotically stable.

Lemma 2.2. (See [23] ). If, , and are all positive and continuous T periodic functions for all, then the system

(2.2)

has a positive T periodic solution which is globally asymptotically stable with respect to

.

Theorem 2.1. System (1.2) is uniformly persistent and has at least one positive T periodic solution provided that

, (2.3)

where is the unique positive periodic solution of system (2.2) given by Lemma 2.2.

We need the following propositions to prove Theorem 2.1.

Proposition 2.1. There exists a positive constant and such that

Proof. Obviously, is a positively invariant set of system (1.2). Given any solution of system (1.2) with initial conditions (1.3), we have

,

.

Consider the following auxiliary system:

(2.4)

By Lemma 2.2, system (2.4) has a unique globally attractive positive T periodic solution. Let be the solution of system (2.4) with. By the vector comparison theorem [24] , we have

(2.5)

From the global attractivity of, for any positive constant (), there exists a T₁ > 0, such that for all

(2.6)

By applying (2.5) and (2.6), we obtain, ,. Let, we have. In addition, from the third equation of (1.2) we have

,

for all. Consider the following auxiliary equation:

(2.7)

By Lemma (2.1), we obtain that system (2.7) has a unique positive T periodic solution which is globally asymptotically stable. Similarly to the above analysis, for the above, there exists a, such that

(2.8)

Set, then.

Proposition 2.2. There exists a positive constant, such that

Proof. By Proposition 2.1, there exists a positive such that,.Hence, from the first and second equations of system (1.2), we obtain

,

for. By Lemma 2.2, the following auxiliary system

(2.9)

has a unique global attractive positive T periodic solution. Let be the solution of system (2.9) with, by the vector comparison theorem, we obtain

(2.10)

Moreover, from the global attractivity of, there exists a, such that

(2.11)

Combined (2.10) with (2.11), we have

Therefore, ,.

Proposition 2.3. Suppose that (2.3) holds, then there exists a positive constant, such that any solution of system (1.2) with initial conditions (1.3) satisfies

(2.12)

Proof. By assumption (2.3), we can choose arbitrarily small constant (without loss generality, we as-

sume that, where is the unique positive periodic solution of sys-

tem (2.2)), such that

, (2.13)

where. Consider the following system with a parameter,

(2.14)

By Lemma 2.2, system (2.14) has a unique positive T periodic solution, which is globally

attractive. Let be the solution (2.14) with initial condition. Then, for the above, there exists a sufficiently large such that, for,

. Using the continuity of the solution in the parameter, we have uniformly in

as. Hence, there exists a such that, for, ,. So, we get Choosing a

constant (,), we obtain

(2.15)

Suppose that the conclusion (2.12) is not true, then there exists such that

, (2.16)

where is the solution of system (1.2) with initial condition

,. So, there exists such that

, (2.17)

for. Then, from the first and second equation of system (1.2), we have

(2.18)

for all. Let be the solution of system (2.14) with and

, then we have

By the global asymptotic stability of, for the given, there exists, such that

So, , ,. By using (2.15), we obtain

(2.19)

Therefore, by using (2.17) and (2.19), for it follows:

(2.20)

Integrating (2.20) from to t yields

.

Thus, from (2.13) we know that as, which is a contradiction. The proof is complete. □

Proof of Theorem 2.1. By Propositions2.2 and 2.3, system (1.2) is uniform weakly uniformly persistent. From Propositions 2.1 and Theorem 1.3.3 in [25] , system (1.2) is uniformly persistent. Using result given by Xu, Chaplain and Davidson in [26] or Wang and Zhu in [27] , we obtain system (1.2) has at least one positive T periodic solution. This completes the proof of Theorem 2.1.

3. Extinction

In this section, we investigate the extinction of the predator population in system (1.2) with initial conditions (1.3) under some condition.

Theorem 3.1. In system (1.2), suppose that

, (3.1)

where is the unique positive periodic solution of system (2.2) given by Lemma 2.2, then

.

Proof. According to (3.1), for every given positive constant , there exists and such that

. (3.2)

From the first and second equations of system (1.2), we have

,

,

Hence, for the above there exists a, such that

(3.3)

It follows from (3.2) and (3.3), that for,

. (3.4)

First, we show that exists a, such that. Otherwise, by (3.4), we have

as.

That is to say. This is a contradiction. Second, we show that

(3.5)

where is bounded for. Otherwise, there exists a, such that. By the continuity of, there must exist a

such that and for. Let be the nonnegative integer such that. According to (3.3), we have

which is a contradiction. This shows that (3.5) holds. By the arbitrariness of, it follows immediately that as. This completes the proof of Theorem 3.1.

From Theorem 2.1 and 3.1, we obtain that the density dependent coefficient has no influence on permanence and extinction of system 1.2. But, from the following simulation, we can know the density dependent coefficient has effect on the populations’ densities of system (1.2).

4. Examples

In this section, we provide some examples to illustrate the feasibility of our main results in Theorems 2.1 and 3.1 and then explore the effect of density dependent coefficient.

Example 4.1. Let

(4.1)

In this case, system (2.2) given by Lemma 2.2 has a unique positive periodic solution

. Furthermore, by a simple calculation, we have

.

Let, according to Theorem 2.1, system (1.2) with the above coefficients is uniformly persistent and admits at least one positive 2π-periodic solution. Figure 1 shows the dynamic behavior of system (1.2).

Let, according to Theorem 2.1, system (1.2) with the above coefficients is uniformly persistent and admits at least one positive 2π-periodic solution. Figure 2 shows the dynamic behavior of system (1.2).

From Theorem 2.1, we know that the density dependent coefficient has no influence on the uniform persistence of system (1.2). However, from Figure 1 and Figure 2, we can see that the density dependent coefficient affects the populations’ densities of system (1.2). Figure 1 demonstrates that the system have high densities with the low density dependent coefficient; whereas Figure 2 shows the system have low densities with the high density dependent coefficient.

Example 4.2. Let

(4.2)

In this case, by a simple calculation, we obtain. According

to Theorem 3.1, system (1.2) is impermanent and the predator population experiences extinction. The numerical simulation shown in Figure 3 also confirms this result.

5. Conclusion

In this paper, we propose a stage-structured predator-prey system with time delay and density-dependent juve-

nile growth. We explore the uniformly persistent and extinction of system (1.2). By Lemma 2.2, we know that is the globally attractive periodic solution of system (1.1) without density dependence and predation. Hence, condition (2.3) implies that system (1.2) is uniformly persistent if the death rate of the predator population is sufficiently small. Numerical simulations not only show the consistency with the theoretical analysis but also exhibit other interesting biological phenomenon. Form Figure 1, Figure 2, we know that although the density dependent coefficient has no influence on the permanence of system (1.2), it affects the system populations’ densities.

Funding

This work was supported by the National Natural Science Foundation of China (No. 31370381), the General Project of Educational Commission in Sichuan Province (Grant No. 16ZB0357), the Major Project of Educational Commission in Sichuan Province (Grant No.16ZA0357) and the Major Project of Sichuan University of Arts and Science (Grant No.2014Z005Z).

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References