Abstract

An all-optical 3:8 decoder unit with the help of terahertz optical asymmetric demultiplexer (TOAD) is proposed. The all-optical 3:8 decoder unit with a set of all-optical full-adders and optical exclusive-ORs (XORs), can be used to perform a fast central processor unit using optical hardware components. We try to exploit the advantages of TOAD-based optical switch to design an integrated all-optical circuit which can perform decoding of signal. A theoretical model is presented and verified through numerical simulation. The new method promises both higher processing speed and accuracy. The model can be extended for studying more complex all-optical circuit of enhanced functionality in which decoder is the basic building block. The operation of the proposed circuit is parallel in nature. The impact of the switching energy with small signal gain and variation of extinction ratio and contrast ration with control pulse energy of the switching outcome is explored and assessed by means of numerical simulations.

Keywords

Terahertz Optical Asymmetric Demultiplexer, Semiconductor Optical Amplifier, Optical Logic

Share and Cite:

Received 26 May 2016; accepted 25 July 2016; published 28 July 2016

1. Introduction

The development of different ultrafast all-optical switches has received considerable interest all over the world in recent years for future optical computing and information processing. The emergence of increasingly high speed, digital optical systems and optical processors demands an all-optical arithmetic unit to perform a set of optical arithmetic micro-operations. All-optical arithmetic units have many potential applications in optical communication systems and optical computing. Various architectures, algorithms, logical, and arithmetic operations have been proposed in the field of optical-optoelectronic computing and parallel signal processing in the past few decades [1] - [7] . A revolution has been brought about in all-optical information processing system with the help of the discovery of ultra high speed all-optical switches based on cross phase modulation. Among different optical switches, the terahertz optical asymmetric demultiplexer (TOAD) gate effectively combines fast switching time, high repetition rate, and low power consumption [8] - [10] . An all-optical half-adder using SOA-assisted Sagnac interferometer has been suggested and demonstrated by several groups of researches [1] [11] - [15] . Ghosh et al. have reported a new method of implementing all-optical frequency encoded logic operations and half-adder by the use of SOA as well as Mach-Zehnder interferometer [16] . A novel scheme for an ultra- high speed all-optical half-adder based on four waves mixing in semiconductor optical amplifiers has been demonstrated by Li [17] . Kim et al. have demonstrated how all-optical full-adder utilizes the mechanism of cross-gain modulation [18] . All-optical full-adder with bit differential delay has been reported by Poustie [19] . A complete analytical model of all-optical half-adder and full-adder has been proposed based on the principle of phase encoding technique [20] . Ghosh et al. have proposed a new scheme of implementing a wavelength encoded complete binary full-adder and full-subtractor unit in all-optical domain using the wavelength conversion by the nonlinear polarization rotation in a single semiconductor optical amplifier [21] . A novel frequency encoded all-optical half-adder, half-subtractor, and full-adder have been suggested by Mukherjee [22] . J. Wang et al. have proposed all-optical simultaneous half-adder, half-subtractor, and OR logic gate at 40 Gbit/s based on the cascaded sum and difference-frequency generation using periodically poled lithium niobate waveguide [23] . Cascading of two TOAD based switches has been demonstrated by B. C. Wang [7] . A terahertz-optical-asymmetric demultiplexer (TOAD)-based gate has already taken a significant role in the field of ultrafast all-optical information processing.

In this paper, we have tried to take the output from both the transmitting and reflecting mode of the device. That is, light coming out from both the input and the output ports is taken into account. With the help of TOAD-based switches, we propose decoder unit that can work in all-optical domains. The proposed all-optical schemes can exhibit its switching speed far above present-day electronic circuits. The operation of the proposed circuit is parallel in nature.

2. Operation of TOAD Based Switch

The basic design of TOAD based switch is shown in Figure 1(a) [8] [24] . Here a nonlinear element (NLE) is placed asymmetrically in a loop. The coon NLE is semiconductor optical amplifier (SOA). In this paper, we have tried to use the output from both the transmitting and reflecting mode of the device. The output power at upper and lower can be expressed as [8] [25]

(1)

(2)

where, is the power gain. The time-dependent phase difference between clockwise (CW) and counter clockwise (CCW) pulses [25] is. with α being the line-width enhancement factor. In the absence of a control signal, data signal (incoming signal) enters the fiber loop, pass through the SOA at different times as they counter-propagate around the loop, and experience the same unsaturated small amplifier gain G_ss, and recombine at the input coupler i.e. G_ccw ≈ G_cw. Then, and expression for and. It shows that data is reflected back toward the source. When a control pulse is injected into the loop (CP=on), it saturates the SOA at time 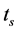and changes its index of refraction. The gain of the SOA decreases rapidly as [25] [26] :

(3)

where is the saturation energy of the SOA, is the unsaturated single-pass amplifier gain and

is the energy fraction contained in the leading edge of the pulse until the moment. By definition = total energy of the control pulse. Here we consider Gaussian pulse as control signal. is the control pulse energy. is related to full width at half maximum (FWHM) by. Then we can write

(4)

where erf(.) is the error function. The SOA saturation time, then 99% of the pulse transmits through SOA. As a while the gain recovers due to injection of carriers and can be obtained from the gain recovery formula [25] [26] ,

(5)

where, is the gain recovery time. When periodic pulse train inserted in the SOA, then there is no time to recovery of the gain to, but to a lower one [25] [26] . Hence Equation (3) takes the form,

(6)

Now, from the above equation we find,

(7)

Now at next bit period (), SOA gain does not reach to but. So,

(8)

For the next pulse, gain starts to reduce again and same process is repeated. As a result, the two counter- propagation data signal will experience differential gain saturation profiles i.e.. We can define the gain ratio [25] [26]

(9)

where T is the eccentricity of the loop. Therefore when they recombine at the input coupler, then and the data will exit from the upper port i.e. and, the corresponding values can be obtained from the Equations ((1) and (2)), respectively. The energy of the control pulse is ten times greater than that of the incoming pulse. A filter may be used at the output of TOAD based switch to reject the control and pass the incoming pulse. The schematic diagram of TOAD based switch is shown in Figure 1(b).

3. All-Optical 3:8 Decoder

A decoder is a combinational circuit that converts binary information from n input lines to a maximum of 2ⁿ unique output lines. The only inputs in decoders are the control bits. In digital electronics, a decoder can take the form of a multiple-input, multiple-output logic circuit that converts coded inputs into coded outputs, where the input and output codes are different e.g. n to 2ⁿ. A block diagram of 3:8 decoder (3 input lines and 8 output lines) is shown in Figure 2. To implement the optical 3:8 decoder, we use TOAD-based optical switches, namely s₁ to s₁₂ as shown in Figure 2 which has three select inputs (A, B and C). It is to be noted that the output of a TOAD-based switch can be used as a control signal for the other provided its intensity is increased suitably through an erbium-doped fiber amplifier and the wavelength is changed through a wavelength converter. The solid lines indicate that the output of one switch is directly connected to input of another switch. The dotted lines indicate that the output of one switch is connected to input of another via wavelength converted and erbium-doped fiber amplifier.

When 1 i.e. presence of incoming signal and A is incident on s₁, light emerging through the upper channel is A and light emerging through lower channel is A̅. Similarly, when 1 and C is incident on s₂, light emerging through the upper channel is C and light emerging through lower channel is C̅. Again when 1 and B are incident on s₃, light emerging through the upper channel is B and light emerging through lower channel is B̅. Finally when 1 and C are incident on s₄ light emerging through the upper channel is C and light emerging through lower channel is C̅.

Again, When A and C are incident on s₅, light emerging through the upper channel is AC and light emerging through lower channel is AC̅. Similarly when A̅ and C̅ are incident on s₆, light emerging through the upper channel is A̅C̅ and light emerging through lower channel is A̅C. Again when B and C are incident on s₇ light emerging through the upper channel is BC and light emerging through lower channel is BC̅. Finally when B̅ and C̅ are incident on s₈ light emerging through the upper channel is B̅C̅ and light emerging through lower channel is B̅C. The eight cases are described in detail.

Case 1: When AC and BC are fed into s₉, light emerging through the upper channel is ABC.

Case 2: When AC and BC are fed into s₉, light emerging through the lower channel is AC(B̅+C̅)=AB̅C.

Case 3: When AC̅ and BC̅ are fed into s₁₀, light emerging through the upper channel is ABC̅.

Case 4: When AC̅ and BC̅ are fed into s₁₀, light emerging through the upper channel is AC̅(B̅+C)=AB̅C̅.

Case 5: When A̅C̅ and B̅C̅ are fed into s₁₁, light emerging through the upper channel is A̅B̅C̅.

Case 6: When A̅C̅ and B̅C̅ are fed into s₁₁, light emerging through the upper channel is A̅BC̅.

Case 7: When A̅C and B̅C are fed into s₁₂, light emerging through the upper channel is A̅B̅C.

Case 8: When A̅C and B̅C are fed into s₁₂, light emerging through the upper channel is A̅BC.

The above observations are put in a table as shown in Table 1. This verifies the operation of 3:8 decoder.

4. Simulated Results

The parameters used in this simulation are taken from the literature survey of different research papers [1] [2] [25] [26] . The values of different parameters as : unsaturated amplifier gain of the SOA (G_ss) = 30 dB, gain recovery time of SOA (τ_e) = 90 ps, saturation energy of the SOA (E_sat) = 1000 fJ, eccentricity of the loop (T_asym) = 30 ps, line-width enhancement factor (α) = 6, full width at half maximum of control pulse (σ) = 6 ps, bit period (T_c) = 100 ps, and a control pulse energy (E_cp) = 100 fJ so that the operational conditions are satisfied. The simulated input waveforms are shown in Figure 3. The simulated output waveforms are shown in Figure 4.

To study the operation of the circuit, we find the appropriate value of the SOA small signal gain for which switching energy is minimized. For this reason, the switching energy’s dependence on the small signal gain is plotted in Figure 5. It can be seen from this figure that the energy decreases exponentially with the increase of small signal gain and reaches a minimum value of 100 fJ at 20 dB.

This is an expected behavior of the switch, since higher small signal gain values drastically affect the SOA dynamics and can induce larger differential gain between the counter-propagating clock components, so that switching can be achieved with less energy. Inversely, a larger energy is required to compensate for the decrease of small signal gain and deeply saturate the SOA, so that the necessary gain changed is occurred.

In order to assess the performance of the circuit at 20 Gbit/s, we define different suitable metrics for this purpose. The most suitable metrics are the extinction ratio and contrast ratio. The extinction ratio (ER) is define as

, (10)

where and is the minimum and maximum peak power of the 1-states and 0-states, respectively, and the contrast ratio (CR) is

, (11)

where and is the mean of the peak power of the 1-states and 0-states, respectively. For high performance these two metrics should lie at least in the vicinity of 8.5 dB, so that the 1-states can be clearly distinguished from the 0-states (ER), while the largest fraction of the incoming data signal exits at the target output of the circuit (CR) [27] . Figure 6 and Figure 7 show the effect on the ER and CR of different control pulse energy, while keeping other parameters constant. The control pulse energy is required to achieve a differential phase shift of π between the counter-propagating incoming pulses and hence full constructive interference at the output. The role of this energy is thus very important, since only at a phase shift of π can transfer the incoming pulses to outputs. The common characteristic of all curves is that both ER and CR increase with increasing control pulse energy up to a certain value after which these metrics are decreased smoothly. This happens because when control

pulse energy is reduced from some specified value then it cannot alter significantly the SOA properties, that is insufficient to create the necessary differential shift and hence reduces the matrices variation.

On the other hand, if the control pulse energy is increased from some specified value (~100 fJ) then the SOA becomes strongly saturated so that the counter clock-wise pulse has enough time to see a partly recovered gain, that is also insufficient to create the necessary differential shift and hence reduces the matrices variation.

From Figures 5-7 and their explanation, it can be inferred that the requirements for the critical parameters are G_ss = 20 dB, τ_e = 100 ps, E_cp = 100 fJ, E_sat = 1000 fJ, T_asym = 30 ps, α = 6, σ = 12 ps, and x = 50 ps respectively, which obviously is not unique and falls within the specified boundaries. Then by combining these values with those held constant throughout the simulation, we can obtain ER = 8.71 dB and CR = 11.67 dB at outputs respectively of the circuit configuration. Therefore all considered performance metrics are more that acceptable, which is reflected on the quality of the pulse stream obtained at the outputs [28] . The eye-diagram [29] is the superposition of the outputs for the repetition period of the inputs. The high quality of the obtained pseudo-eye diagram (PED) is further supported by its relative eye opening (O) defined as, and are the minimum and maximum powers at 1-state and 0-state, respectively. An eye-diagram with large eyes indicates a clear transmission with a low bit error rate. Here, we get PED (O) = 82.88% at the outputs, respectively, which indicates an excellent response of the circuit to the incoming data at its output terminals.

5. Conclusion

In this paper, we have reported all-optical 3:8 decoder. The proposed scheme has been verified with numerical simulations. We have tried to take the output from both the transmitting and reflecting mode of the device. That is, light coming out from both the input and the output ports is taken into account. Variation of the switching energy’s dependence on the small signal gain is also discussed in this paper. By conducting numerical simulation, we have specified the requirements for the control pulse energy, gain recovery time and input pulse width so that the performance metrics of extinction ratio, contrast ratio and relative opening of the pseudo-eye diagram are acceptable. We obtain ER = 8.71 dB, CR = 11.67 dB and PED (O) = 82.88%, which indicates an excellent response of the circuit to the incoming data at its output terminals. This circuit can be used to design many complex all-optical circuits. The model can be extended for studying more complex all-optical circuits of enhanced functionality in which the proposed circuit developed in this paper may be assumed as the basic building blocks.

Acknowledgements

The authors are grateful to Technical Education Quality Improvement Programme (TEQIP) phase II by National Project Implementation Unit (Approval No.―CEMK/TEQIP-lI/R&D/Project/15-16/03) for providing the grant for this work.

Conflicts of Interest

The authors declare no conflicts of interest.

References