Resolution of Resource Contentions in the CCPM-MPL Using Simulated Annealing and Genetic Algorithm ()
1. Introduction
2. CCPM-MPL Framework
After defining the max-plus algebra, we define the CCPM-MPL framework with the help of [1] and [2] .
2.1. Max-Plus Algebra
We define a set , where
, where  is the whole real line. Then, for
is the whole real line. Then, for  , we define the operators:
, we define the operators:
 (1)
(1)
 (2)
(2)
The priority of operator  is higher than that of
is higher than that of . If
. If 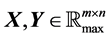 and
and ,
,
 (3)
(3)
 (4)
(4)
The zero and unit elements for operators 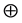 and
and  are denoted by
are denoted by  and
and , respectively.
, respectively.  is a matrix whose elements are all
is a matrix whose elements are all , and
, and 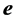 is a matrix whose diagonal elements are
is a matrix whose diagonal elements are ![]() and whose off-diagonal elements are
and whose off-diagonal elements are![]() . If
. If![]() , the following operator
, the following operator ![]() is the Kleene star:
is the Kleene star:
![]() (5)
(5)
where ![]() is an instance that satisfies
is an instance that satisfies ![]() and
and![]() . In addition, we define
. In addition, we define
![]() (6)
(6)
2.2. Formulation of the CCPM-MPL Framework
We define the following relevant matrices and vectors:
・ n: number of tasks;
・ ![]() : number of external outputs;
: number of external outputs;
・ ![]() : number of external inputs;
: number of external inputs;
・ ![]() : input matrix,
: input matrix, ![]() = {e: if task i has an input transition j, ε: otherwise};
= {e: if task i has an input transition j, ε: otherwise};
・ ![]() : output matrix,
: output matrix, ![]() = {e: if task j has an output transition i,
: otherwise};
= {e: if task j has an output transition i,
: otherwise};
・ ![]() : adjacency matrix,
: adjacency matrix, ![]() = {e: if task i has a preceding task j, ε: otherwise};
= {e: if task i has a preceding task j, ε: otherwise};
・ ![]() : system parameter,
: system parameter,![]() : duration time in task i;
: duration time in task i;
・ ![]() : input vector,
: input vector,![]() : input time to external input i;
: input time to external input i;
・ ![]() : output vector,
: output vector,![]() : output time from external output i;
: output time from external output i;
・ ![]() : state vector,
: state vector,![]() : start or completion time of task i.
: start or completion time of task i.
The earliest task-completion times of all tasks, ![]() , are calculated using
, are calculated using
![]() (7)
(7)
where
![]() (8)
(8)
![]() (9)
(9)
Matrixes ![]() and
and ![]() are the transition and weight matrices, respectively. The earliest output times to all output transitions,
are the transition and weight matrices, respectively. The earliest output times to all output transitions, ![]() , are then calculated by
, are then calculated by
![]() (10)
(10)
Then, the latest task-starting times, ![]() , are calculated using Equation (10):
, are calculated using Equation (10):
![]() (11)
(11)
The latest input times, ![]() , are calculated in terms of
, are calculated in terms of![]() :
:
![]() (12)
(12)
As a consequence, the total floats of all tasks can be calculated using Equations ((5) and (8)):
![]() (13)
(13)
All tasks can be classified into two types: ![]() and
and ![]() are a critical and a non-critical task, respectively. We define two vectors,
are a critical and a non-critical task, respectively. We define two vectors, ![]() , to classify each task as either critical or non-critical:
, to classify each task as either critical or non-critical:
![]() (14)
(14)
![]() (15)
(15)
We then calculate two matrices, ![]() , as follows:
, as follows:
![]() (16)
(16)
![]() (17)
(17)
In the CCPM framework, there are two types of buffers, referred to as feeding and project buffers. The size of each buffer is calculated by
![]() (18)
(18)
![]() (19)
(19)
where
![]() (20)
(20)
Feeding buffers are inserted wherever a non-critical task joins into a critical one. A project buffer is inserted on the eve of an output to avoid tardiness of the project. To reflect the insertion of the two types of buffers, we incur weights to the adjacency matrix ![]() and the output matrix
and the output matrix![]() :
:
![]() (21)
(21)
![]() (22)
(22)
Now we can calculate the earliest task-completion, ![]() , and the output time,
, and the output time, ![]() , after inserting the time buffers. The earliest task-completion times of all nodes,
, after inserting the time buffers. The earliest task-completion times of all nodes, ![]() , are calculated using
, are calculated using
![]() (23)
(23)
![]() (24)
(24)
Matrix ![]() is the transition matrix, in which the insertion of the two types of buffers is reflected. The earliest output times to all output transitions,
is the transition matrix, in which the insertion of the two types of buffers is reflected. The earliest output times to all output transitions, ![]() , are then calculated by
, are then calculated by
![]() (25)
(25)
We treat ![]() as the objective function and consider minimizing
as the objective function and consider minimizing![]() .
.
3. Resolution of Resource Contentions
We explain the resolution of resource contentions with the help of [8] . We add relevant matrices and vectors as follows:
・ ![]() : number of resources,
: number of resources,
・ ![]() : maximum number of tasks that a single resource processes,
: maximum number of tasks that a single resource processes,
・ ![]() : processing order of tasks,
: processing order of tasks,
![]() .
.
We consider Figure 1 as an example project with five tasks before the leveling of resource contentions. The duration time of each task is![]() . The adjacency matrix,
. The adjacency matrix, ![]() , is
, is
![]() (26)
(26)
Tasks 1, 4, and 5 are processed by resource 1, whereas tasks 2 and 3 are processed by resource 2. If resource 2 processes tasks 2 and 3 simultaneously, a resource contention occurs. We avoid contentions between tasks 2 and 3 by appending two precedence relations, which are expressed by broken arrows in Figure 2, which shows the project after the resource contention is leveled. We then reflect the leveling of the resource contentions using the following adjacency matrix,![]() :
:
![]() (27)
(27)
In addition, the processing order of tasks, ![]() , is
, is
![]() (28)
(28)
Our numerical simulation to level resource contentions shows that the maximum
![]()
Figure 1. Example of a fifth-task project before a resource contention is leveled.
![]()
Figure 2. Example of the fifth-task project after the resource contention is leveled.
computation time was longer than 10 hours for 20 jobs. We thus consider the development of approximate methods within a short computation time.
4. Two Metaheuristics
We experiment with an optimization based on Genetic Algorithm (GA) and Simulated Annealing (SA), both of which are common metaheuristics.
4.1. Genetic Algorithm
We experiment with an optimization based on the GA developed in [6] , which is used to obtain an approximate solution.
Algorithm 1: Genetic Algorithm
STEP 1. Set mutation parameter and termination condition, ![]() and
and![]() , respectively.
, respectively.
STEP 2. Generate a random solution, ![]() , and create the earliest output times,
, and create the earliest output times,![]() .
.
STEP 3. Focusing on a row vector of ![]() that gives the list of tasks for a single resource, split the vector into two. We then swap the two vectors, followed by generating a new solution,
that gives the list of tasks for a single resource, split the vector into two. We then swap the two vectors, followed by generating a new solution,![]() .
.
STEP 4. If a mutation occurs having probability![]() , then proceed to STEP 5. Otherwise, i.e., if a mutation does not occur, then follow STEP 6.
, then proceed to STEP 5. Otherwise, i.e., if a mutation does not occur, then follow STEP 6.
STEP 5. Swap two tasks of ![]() at the same resource randomly.
at the same resource randomly.
STEP 6. Create the new earliest output times, ![]() using
using![]() .
.
STEP 7. If ![]() follows, then set
follows, then set ![]() and
and![]() .
.
STEP 8. Terminate if the termination condition is satisfied. If otherwise, return to STEP4.
4.2. Simulated Annealing
SA [9] is known as an approach to efficiently obtain an approximate solution. We use the 2-opt neighborhood method [10] based on a local search to generate a neighboring solution.
Algorithm 2: Simulated Annealing
STEP 1. Initialize the temperature and cooling parameters, ![]() and
and![]() , respectively.
, respectively.
STEP 2. Generate a random solution, ![]() , and create the earliest output times,
, and create the earliest output times,![]() .
.
STEP 3. Generate a neighboring solution, ![]() , and create the new earliest output times,
, and create the new earliest output times,![]() .
.
STEP 4. Calculate![]() .
.
STEP 5. If ![]() holds, then set
holds, then set ![]() and
and ![]() with probably 1. Otherwise, i.e., if
with probably 1. Otherwise, i.e., if ![]() holds, then set
holds, then set ![]() and
and ![]() with probably
with probably![]() .
.
STEP 6. Update the temperature parameter,![]() .The value of
.The value of ![]() is a cooling parameter which decreases the temperature parameter,
is a cooling parameter which decreases the temperature parameter,![]() .
.
STEP 7. Repeat STEPS3-6.
STEP 8. Terminate if the temperatures are sufficiently low. If otherwise, return to STEP3.
5. Approximate Ratio and Computation Time
We obtain solutions using the SA- and GA-based algorithms. We use a personal computer with the following execution environment:
・ machine: Dell Optiplex 9020;
・ CPU: Intel® Core™ i7-4790 3.60 GHz;
・ OS: Microsoft Windows 7 Professional;
・ memory: 4.0 GB;
・ programming language: MATLAB R2015b.
The test cases for the numerical experiment are generated under the following conditions:
・ number of cases: 100;
・ number of resources,![]() : for 10, 15, and 20 tasks, we set the number of resources to 3, 5, and 7, respectively;
: for 10, 15, and 20 tasks, we set the number of resources to 3, 5, and 7, respectively;
・ number of resources for task,![]() : uniformly random integer numbers;
: uniformly random integer numbers;
・ duration time,![]() : uniformly random integer numbers.
: uniformly random integer numbers.
We obtain approximate solutions using two metaheuristics. The temperature and cooling parameter are set to ![]() and
and![]() , respectively, for the SA-based algorithm. The mutation parameter and the end condition are set to
, respectively, for the SA-based algorithm. The mutation parameter and the end condition are set to ![]() and
and![]() , respectively, for the GA-based algorithm. We compare the exact and approximate solutions. The performance of the solution is shown in Table 1 for the two metaheuristics. We can confirm that the performance of the solution using the GA-based algorithm is smaller than that using the SA-based algorithm. The average computation times are shown in Figure 3. We can confirm that the computation using the SA-based algorithm is faster than that using the GA-based algorithm. The computation time of the GA-based algorithm is more than16-fold longer than that of the SA-based algorithm. The average values of the solutions are shown in Table 2. If the number of tasks is 10 or 20, the values of the solutions using the two methods are not remarkably different; if the number of tasks is 30 or 40, the value of the solution using the GA-based algorithm is smaller than that of the SA-based algorithm. However, we should note
, respectively, for the GA-based algorithm. We compare the exact and approximate solutions. The performance of the solution is shown in Table 1 for the two metaheuristics. We can confirm that the performance of the solution using the GA-based algorithm is smaller than that using the SA-based algorithm. The average computation times are shown in Figure 3. We can confirm that the computation using the SA-based algorithm is faster than that using the GA-based algorithm. The computation time of the GA-based algorithm is more than16-fold longer than that of the SA-based algorithm. The average values of the solutions are shown in Table 2. If the number of tasks is 10 or 20, the values of the solutions using the two methods are not remarkably different; if the number of tasks is 30 or 40, the value of the solution using the GA-based algorithm is smaller than that of the SA-based algorithm. However, we should note
![]()
Table 1. Performance of the solutions.
![]()
Table 2. Average values of the solutions.
![]()
Figure 3. Average computation times in seconds.
here that the solution using the SA-based algorithm is better than that using the GA if the number of tasks is 50.
6. Conclusions
This research has studied the planning of a “good-enough” schedule with leveling of resource contentions. We utilized an existing framework called the CCPM-MPL. The resolution framework was reduced to a combinatorial problem. We used SA- and GA-based algorithms to obtain approximate solutions within short time. Moreover, we used the 2-opt neighborhood to generate a neighboring solution in the SA-based algorithm. Comparing the two methods, the SA-based algorithm was beneficial in terms of computation time, whereas the latter was better in terms of the performance of the solution. In addition, when the number of tasks was 50, the value of the solution using the SA-based algorithm was better than that using the GA-based algorithm.
Developing an original heuristic to level resource contentions within a short computation time is our future work.