Revolving Ferrofluid Flow under the Influence of MFD Viscosity and Porosity with Rotating Disk ()
1. Introduction
For centuries, many fascinating materials have been attracting the scientists and researchers due to their extraordinary physical properties and technological usage. Ferrofluid is one of such smart materials, not available in free state in nature, but are to be synthesized. These fluids have variety of applications in the field of sciences and engineering like instrumentation, electrical and electronics engineering etc. which are being commercialized.
Ferrofluids are widely used in sealing of computer hard disk drives, rotating X-ray tubes, rotating shafts and rods. These are used as lubricants in bearing and dumpers. Also ferrofluids are used as heat controller in electric motors and hi-fi speaker systems without the need of change in their geometrical shape. Ferrofluids are being greatly used in many magnetic fluid based scientific devices like sensors, densimeters, accelerometer, pressure transducers etc. and also in actuating machines like electromechanical converters and energy converters etc.
In field of biomedicine also, they have been found very useful. These can be used to deliver certain drugs to a certain area of human body. There is also an idea to use ferrofluids for cancer treatment by heating the tumor soaked in ferrofluids by means of an alternating magnetic field. One of the many fascinating features of the ferrofluids is the prospect of influencing flow by the magnetic field and vice-versa [1,2].
There are rotationally symmetric flows of the incompressible ferrofluids in the field of fluid mechanics, having all three velocity components; radial, tangential and vertical in space different from zero. In such types of flow, the variables are independent of the angular co-ordinates and the angular velocity is uniform at large distance from the disk (Figure 1).
We consider this type of flow for an incompressible ferrofluid; when the disk is subjected to the magnetic field  using NR model [3]. This model has been used by Verma et al. [4-6] for solving paramagnetic Couette flow, helical flow with heat conduction and flow
using NR model [3]. This model has been used by Verma et al. [4-6] for solving paramagnetic Couette flow, helical flow with heat conduction and flow
through a porous annulus. Rosensweig [7] has given an authoritative introduction to the research on magnetic liquids in his monograph and studied the effect of magnetization, resulting in interesting information.
A study of flow within the boundary layer and its effect on the general flow around the body, in detail, are given in Schlichting [8]. The pioneering study of ordinary viscous fluid flow due to the infinite rotating disk was carried by Karman [9]. He introduced the famous transformation which reduces the governing partial differential equations into ordinary differential equations. Karman’s rotating disk problem is extended to the case of flow started impulsively from rest and the steady state is solved to a higher degree of accuracy than previously done by a simple analytical method which neglects the resembling difficulties in Cochran’s [10] well known solution. Cochran obtained asymptotic solutions for the steady hydrodynamic problem formulated by Karman. Benton [11] improved Cochran’s solutions, and also, solved the unsteady case. Attia [12] studied the unsteady state in the presence of an applied uniform magnetic field. The steady flow of ordinary viscous fluid due to the rotating disk with uniform high suction was studied by Mithal [13]. Attia [14] discussed about flow due to an infinite disk rotating in the presence of an axial uniform magnetic field by taking Hall effect into consideration.
Attia [15] studied the steady flow of an incompressible viscous fluid above an infinite rotating disk in a porous medium with heat transfer and also discussed the effect of porosity of the medium on the velocity and temperature distribution. Frusteri and Osalusi [16] examined the laminar convective and slip flow of an electrically conducting Newtonian fluid with variable properties over a rotating porous disk.
Using linear instability analysis, Venkatasubramanian and Kaloni [17] discussed the effects of rotation on the onset of convection in a horizontal layer of ferrofluids rotating about its vertical axis, heated from below and in the presence of uniform vertical magnetic field. The effect of an alternating uniform magnetic field on convection in a horizontal layer of a ferrofluid within the framework of a quasi-stationary approach is studied by Belyaev [18]. The effect of magnetic field along the vertical axis on thermo-convective instability in a ferromagnetic fluid saturating a rotating porous medium has been studied by Sekar et al. [19] by using the Darcy model. Ram et al. [20] discussed the various fluid characteristics of ferrofluid flow in porous medium with rotating disk.
In general, magnetization is a function of magnetic field, temperature and density of the fluid. This leads to convection of ferrofluid in the presence of the magnetic field gradient. Viscosity is also one of the astounding rheological properties of ferrofluid influencing convection flow problems. Detail accounts of magneto-viscous effects in ferrofluids have been given in a monograph by Odenbach [21]. Sunil et al. [22] studied the effect of MFD viscosity on thermosolutal convection in a ferromagnetic fluid saturating a porous medium. Sunil et al. [23] discussed the influence of rotation on medium permeability and how MFD viscosity affects the magnetization in ferromagnetic fluid heated from below in the presence of dust particles saturating a porous medium of very low permeability using Darcy model. The effect of MFD viscosity on thermal convection in a ferromagnetic fluid in a porous medium is studied by Sunil et al. [24]. Nanjundappa et al. [25] studied Benard-Marangoni ferroconvection in a ferrofluid layer in the presence of a uniform vertical magnetic field with MFD viscosity. Ram et al. [26] solved the non-linear differential equations under Neuringer-Rosensweig model for ferrofluid flow by using power series approximations and discussed the effect of MFD viscosity on the velocity components and pressure profile. Further, the effect of porosity on velocity components and pressure profile in the presence of rotating disk has been studied by Ram et al. [27]. Turkyilmazoglu [28] discussed the solution of the steady laminar flow of an incompressible viscous electrically conducting fluid over a rotating disk in the presence of a uniform transverse magnetic field and also purely explicit analytical expressions for solution of magnetohydrodynamic equations were obtained via homotopy analysis method.
In the present problem, we take cylindrical co-ordinates , where z-axis is normal to the plane and this axis is being considered as the axis of rotation. The viscous effects are not dominant but inertial effects are the dominant one over a region at a small distance from the disk, if Reynolds number is large, which gives rise to a boundary layer over the surface of the disk. We have solved the boundary layer equations together with Maxwell’s equations theoretically as well as numerically. Also, it is found that in the present problem, there is a large variation in the boundary layer thickness as compared to the ordinary viscous flow case. We have also given an expression for the total volume flowing outwards the axis taken over a cylinder of radius R around the z-axis. The effects of MFD viscosity and porosity parameter in a circular layer of revolving ferrofluid with rotating disk are studied within the framework of the NR approach, and various types of ferrofluid responses are considered. This problem, to the best of our knowledge, has not been investigated yet.
, where z-axis is normal to the plane and this axis is being considered as the axis of rotation. The viscous effects are not dominant but inertial effects are the dominant one over a region at a small distance from the disk, if Reynolds number is large, which gives rise to a boundary layer over the surface of the disk. We have solved the boundary layer equations together with Maxwell’s equations theoretically as well as numerically. Also, it is found that in the present problem, there is a large variation in the boundary layer thickness as compared to the ordinary viscous flow case. We have also given an expression for the total volume flowing outwards the axis taken over a cylinder of radius R around the z-axis. The effects of MFD viscosity and porosity parameter in a circular layer of revolving ferrofluid with rotating disk are studied within the framework of the NR approach, and various types of ferrofluid responses are considered. This problem, to the best of our knowledge, has not been investigated yet.
2. Mathematical Formulation and Solution
Basic Assumptions:
a) The flow is steady and Axi-symmetric.
b) The fluid layer is assumed to be flowing through an isotropic medium of porosity .
.
c) The fluid and the ferrous particles have the same velocity.
d) The fluid and disk are electrically non-conducting.
e) The magnetic field affects only viscosity and not other properties.
f) The thermal effects are excluded.
Basic Constitutive Equations:
The continuity equation is  (1)
(1)
The momentum equation for an incompressible ferro-magnetic revolving fluid in the frame of porosity  and MFD viscosity
and MFD viscosity  where whole system is rotating with angular velocity
where whole system is rotating with angular velocity  is
is
 (2)
(2)
The effect of rotation includes two terms:
a) Centrifugal force 
b) Coriolis acceleration 
In (2)  denotes the reduced pressure, where
denotes the reduced pressure, where  stands for fluid pressure.
stands for fluid pressure.
Maxwell’s equations, simplified for a non-conducting fluid with no displacement currents, become
 (3)
(3)
Assumptions
 (4)
(4)
Considering the velocity component  small as compared to
small as compared to  and
and . The equation of motion and equation of continuity reduce to
. The equation of motion and equation of continuity reduce to
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
where  = Ratio of MFD viscosity and density of the fluid. The approximate initial and boundary conditions for the flow due to rotation of an infinitely long disk
= Ratio of MFD viscosity and density of the fluid. The approximate initial and boundary conditions for the flow due to rotation of an infinitely long disk  with constant angular velocity
with constant angular velocity are given by
are given by
 (9)
(9)
The boundary layer approximation for (5) is as follows.
 (10)
(10)
On considering very less variation of magnetic field along the z-direction and using Karman’s transformations,
 (11)
(11)
where , in Equations (5)-(8) with the help of (11), we get a system of non-linear coupleddifferential equations in E, F, G and P as follows:
, in Equations (5)-(8) with the help of (11), we get a system of non-linear coupleddifferential equations in E, F, G and P as follows:
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
G must tend to a finite limit, say –c as , i.e.
, i.e.
 (17)
(17)
Following Cochran formal asymptotic expansion (for large  ) of the system of Equations (12), (14) and (15), is a power series
) of the system of Equations (12), (14) and (15), is a power series

and Equation (13) is a power series
 , i.e.
, i.e.
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
Using this supposition  and
and  in Equation (12)-(16), we get the additional boundary conditions for the approximate solution for first four coefficients involved in (18)-(21):
in Equation (12)-(16), we get the additional boundary conditions for the approximate solution for first four coefficients involved in (18)-(21):

3. Results and Discussions
Using the values 
 and
and  from Cochran [10], we calculate the values of the coefficients
from Cochran [10], we calculate the values of the coefficients 













 and
and . We draw the graphs of velocity components and asymptotic pressure with the dimensionless parameter
. We draw the graphs of velocity components and asymptotic pressure with the dimensionless parameter  under the effect of MFD viscosity and porosity. The present results give the good approximate solution of the above system of non-linear coupled differential equations.
under the effect of MFD viscosity and porosity. The present results give the good approximate solution of the above system of non-linear coupled differential equations.
The boundary layer displacement thickness is given by

Hence the boundary layer displacement thickness becomes d1 = 0.0233988, d1 = 0.04656773 and d1 = 0.0695072 for 
 and
and  respectively.
respectively.
The total volume flowing outward the z-axis,

Hence from this equation, the total volume flowing outward the z-axis is proportional to the dimensionless parameter  . The fluid is taken to rotate at a large distance from the wall, the angle becomes
. The fluid is taken to rotate at a large distance from the wall, the angle becomes

Figures 2, 3 and 4 show the radial velocity profile with the variation of dimensionless parameter  (Karman’s parameter) for different values of porosity
(Karman’s parameter) for different values of porosity  at MFD viscosity parameter
at MFD viscosity parameter 
 and
and , respectively. The radial velocity at porosity
, respectively. The radial velocity at porosity  for MFD viscosity parameter
for MFD viscosity parameter  without rotation is the reduced case of viscous incompressible problem. For
without rotation is the reduced case of viscous incompressible problem. For  the radial component of velocity
the radial component of velocity  is maximum at
is maximum at  and
and  and
and  have the maximum values
have the maximum values  and
and  at
at  and
and  respectively. Whereas, in Ram et al. [26] case of MFD viscosity without porosity and without rotation;
respectively. Whereas, in Ram et al. [26] case of MFD viscosity without porosity and without rotation; 
 and
and

Figure 2. Effect of porosity ε = 0.01 along with variation of MFD viscosity parameter k on radial velocity.

Figure 3. Effect of porosity ε = 0.02 along with variation of MFD viscosity parameter k on radial velocity.

Figure 4. Effect of porosity ε = 0.03 along with variation of MFD viscosity parameter k on radial velocity.
have the maximum values 0.454648, 0.544554 and 0.590987 at 
 and
and  respectively. Thus, the convergence rate for radial component of velocity is faster for revolving ferrofluid flow with MFD viscosity along with porosity than the case reported in Ram et al. [26] for MFD viscosity only. However, from Figures 2, 3 and 4; we observe that for different increasing values of porosity with same set values of MFD viscosity parameter
respectively. Thus, the convergence rate for radial component of velocity is faster for revolving ferrofluid flow with MFD viscosity along with porosity than the case reported in Ram et al. [26] for MFD viscosity only. However, from Figures 2, 3 and 4; we observe that for different increasing values of porosity with same set values of MFD viscosity parameter , the radial values of velocity lead to its slow convergence.
, the radial values of velocity lead to its slow convergence.
Figure 5 shows the tangential velocity profile for different values of porosity. There is no effect of MFD viscosity on tangential velocity component as we have not considered the effect of magnetic field in tangential direction. Here, for  the tangential velocity components are
the tangential velocity components are 
 and
and  for different values of porosity
for different values of porosity 
 and
and  , respectively. Also, it is observed that due to the effect of porosity, the tangential velocity component is increasing with the increase in Karman’s parameter
, respectively. Also, it is observed that due to the effect of porosity, the tangential velocity component is increasing with the increase in Karman’s parameter  . Whereas in Ram et al. [26] case, the tangential velocity component is free from the effect of porosity. Here, the tangential velocity decreases smoothly and after certain values of
. Whereas in Ram et al. [26] case, the tangential velocity component is free from the effect of porosity. Here, the tangential velocity decreases smoothly and after certain values of  it converges to zero. But, as we increase the value of porosity, the convergence becomes slower.
it converges to zero. But, as we increase the value of porosity, the convergence becomes slower.
Figures 6, 7 and 8, represent the axial velocity profiles which are zero in the beginning. It is clear that when we increase the magnetic-field, the axial velocity goes to more negative region and the component  tends to a negative finite value
tends to a negative finite value  little faster than
little faster than  and
and . For
. For  the axial velocity
the axial velocity  ,
,  and
and  converges to finite negative value
converges to finite negative value  at
at 
 and
and  at MFD viscosity parameter
at MFD viscosity parameter 
 and
and respectively. Whereas, for
respectively. Whereas, for  , the axial components of the velocity
, the axial components of the velocity  ,
,  and
and  at MFD viscosity parameter
at MFD viscosity parameter 
 and
and  converges to this finite negative value at
converges to this finite negative value at 
 and
and  respectively. Similarly, we can conclude for
respectively. Similarly, we can conclude for , the late convergence is appeared for axial velocity components
, the late convergence is appeared for axial velocity components  ,
,  and
and 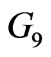 at MFD viscosity parameter
at MFD viscosity parameter 
 and
and  respectively. In Ram et al. [26], the fluctuations in graph are negligible, but here fluctuations are prominent. There is a large variation in axial velocity components for different MFD viscosity parameter along with the effect of porosity and revolution of ferrofluid. Also from the Figures 6, 7 and 8, we can conclude that the axial velocity component is decreasing with increase in porosity and MFD viscosity, but for large values of
respectively. In Ram et al. [26], the fluctuations in graph are negligible, but here fluctuations are prominent. There is a large variation in axial velocity components for different MFD viscosity parameter along with the effect of porosity and revolution of ferrofluid. Also from the Figures 6, 7 and 8, we can conclude that the axial velocity component is decreasing with increase in porosity and MFD viscosity, but for large values of 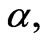 it takes finite negative value
it takes finite negative value .
.
Figures 9, 10 and 11 show the pressure profile with initial pressure P0, for different values of porosity  at MFD viscositiy parameter
at MFD viscositiy parameter 
 and
and  respectively. In Figure 9, the pressure
respectively. In Figure 9, the pressure  reaches to maximum negative value
reaches to maximum negative value  at
at  for
for  and
and  whereas, for the same value of
whereas, for the same value of  the pressures
the pressures  and
and  take the maximum negative values
take the maximum negative values  and
and  at
at  and
and  for
for  and 1.3, respectively. We conclude from these graphs that due to the increment in magnetic field and rotation of ferrofluid, the convergence rate is going slow and slow with the increment in porosity
and 1.3, respectively. We conclude from these graphs that due to the increment in magnetic field and rotation of ferrofluid, the convergence rate is going slow and slow with the increment in porosity along with the variation in Karman’s parameter
along with the variation in Karman’s parameter  Also, in comparison to Ram et al. [26], the pressure decreases due to the effect of porosity and rotation of ferrofluid.
Also, in comparison to Ram et al. [26], the pressure decreases due to the effect of porosity and rotation of ferrofluid.

Figure 5. Effect of porosity ε on tangential velocity.

Figure 6. Effect of porosity ε = 0.01 along with variation of MFD viscosity parameter k on axial velocity.

Figure 7. Effect of porosity ε = 0.02 along with variation of MFD viscosity parameter k on axial velocity.

Figure 8. Effect of porosity ε = 0.03 along with variation of MFD viscosity parameter k on axial velocity.

Figure 9. Effect of porosity ε = 0.01 along with variation of MFD viscosity parameter k on pressure profile.

Figure 10. Effect of porosity ε = 0.02 along with variation of MFD viscosity parameter k on pressure profile.

Figure 11. Effect of porosity ε = 0.03 along with variation of MFD viscosity parameter k on pressure profile.
4. Conclusions
1) Under the influence of MFD viscosity, porosity and rotation, the radial and tangential components of velocity converge to zero faster than in comparison to the case of MFD viscosity alone. The radial velocity increases with increase in porosity and MFD viscosity both, whereas the tangential component of velocity increases with the increase in porosity only and MFD viscosity has no effect on it. The effect of MFD viscosity is dominant in radial direction and is moderate in axial direction.
2) Also, the axial velocity converges to finite negative value faster than the case of MFD viscosity alone. Numerical value of the axial component decreases with increase in porosity and MFD viscosity, both.
3) Pressure profile shows smaller values in comparison to the case of MFD viscosity only. Here, we can also say that the radial velocity and pressure are converse in behavior to each other.
4) The boundary layer displacement thickness becomes very small in comparison to the case of MFD viscosity only as well as to the case of ordinary viscous flow reported in [26] and [11], respectively.
The present study projects certain practical applications in many areas such as rotating machinery, lubrication, oceanography, computer storage devices, and viscometry and crystal growth processes. In nut shell, this problem is the theoretical motivation explaining physical effects of variable field dependent viscosity, porosity and rotation on various flow characteristics of the ferrofluid.
Nomenclature
r |
Radial direction (m) |
θ |
Tangential direction  |
z |
Axial direction (m) |
q |
Velocity of ferrofluid (m/s) |
B |
Magnetic induction  |
Ω |
Angular velocity of whole system (rad/s) |
p' |
Fluid pressure (kg/ms2) |
M |
Magnetization (A/m) |
H |
Magnetic field intensity (A/m) |
ψ |
Potential energy function (kg·m2/s2) |
χ |
Magnetic susceptibility |
vr |
Radial velocity (m/s) |
vθ |
Tangential velocity (rad/s) |
vz |
Axial velocity (m/s) |
ω |
Angular velocity of the disk (rad/s) |
E |
Dimensionless component of radial velocity |
F |
Dimensionless component of tangential velocity |
G |
Dimensionless component of axial velocity |
P |
Karman’s dimensionless pressure |
P0 |
Initial pressure (absolute value) |
k |
Ratio of kinematic variable MFD viscosity and kinematic viscosity (viscosity parameter) |
d |
Thickness of the ferrofluid layer (m) |
Q |
Total volume flowing outward the z-axis (m3) |
Greek Symbols
μ |
Reference viscosity of fluid (kg/ms) |
δ |
Linear measure of the viscosity variations with the applied magnetic field (Tesla–1) |
ρ |
Fluid density (kg/m3) |
ε |
Porosity |
μ |
Magnetic permeability of free space (H/m) |
v1 |
Kinematic variable MFD viscosity (m2/s) |
v |
Kinematic viscosity (m2/s) |
α |
Karman’s dimensionless parameter |