Alfred Olufemi Bosede¹, Hudson Akewe², Omolara Fatimah Bakre³, Ashiribo Senapon Wusu^1
1Department of Mathematics, Lagos State University, Ojo, Nigeria.
²Department of Mathematics, University of Lagos, Akoka, Nigeria.
³Department of Mathematics & Statistics, Federal College of Education (Technical), Akoka, Nigeria.
DOI: 10.4236/jamp.2019.71011   PDF    HTML   XML   630 Downloads   1,312 Views   Citations

Abstract

In this paper, a modified implicit Kirk-multistep iteration scheme and a strong convergence result for a general class of maps in a normed linear space was established. It was also shown that the convergence of this iteration scheme is equivalent to the convergency of some other implicit Kirk-type iteration (implicit Kirk-Noor, implicit Kirk-Ishikawa and implicit Kirk-Mann iterations) for the same class of maps. Some numerical examples were considered to show that the equivalence of convergence results to the fixed point is true. The results unify most equivalence results in literature.

Keywords

Implicit Kirk-Multistep, Implicit Kirk-Mann Iterations, Strong Convergence, Equivalence, General Class of Maps

Share and Cite:

1. Introduction

In 1971, Kirk introduced the Kirk iterative scheme as follows: Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space and D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ be a selfmap of D, let $x_0\in E$ , the sequence ${\left\{x_n\right\}}_{n=1}^{\infty }$ is defined by

$x_{n+1}={\displaystyle \underset{i=0}{\overset{k}{\sum }}}{\alpha }_i{T}^i{x}_n,n\ge 0,{\displaystyle \underset{i=0}{\overset{k}{\sum }}}{\alpha }_i=1$ (1)

Various authors have written inspiring papers on Kirk-type iterative schemes. Worthy to mention are the following: the explicit Kirk-Mann, Olatinwo [1] , explicit Kirk-Ishikawa, Olatinwo [1] , Kirk-Noor, Chugh and Kumar [2] and Kirk-multistep, Akewe, Okeke and Olayiwola [3] iterative schemes.

In 2014, Akewe, Okeke and Olayiwola [3] proposed an explicit Kirk-multistep iterative schemes and proved strong convergence and stability results for contractive-like operators in a normed linear space, the researchers also gave useful numerical examples to back up their schemes. The authors in Chugh, Malik and Kumar [4] made the following statements in their introduction: “Implicit iterations have an advantage over explicit iterations for nonlinear problems as they provide better approximation of fixed points and are widely used in many applications when explicit iterations are inefficient. Approximation of fixed points in computer oriented programs by using implicit iterations can reduce the computational cost of the fixed point problems”. They considered a new implicit iteration and study its strong convergence, stability, and data dependence and also proved through numerical examples that newly introduced iteration has better convergence rate than well known implicit Mann iteration as well as implicit Ishikawa iteration and that implicit iterations converge faster as compared to corresponding explicit iterations. However, it was observed that little work has been done on equivalence of implicit scheme.

The main aim of this work is in three folds: firstly, to develop a modified implicit Kirk-multistep scheme and prove strong convergence results for a general class of mapping introduced by Bosede and Rhoades [5] . Secondly, to show that the convergence of the implicit Kirk-multistep iteration scheme is equivalent to the convergency of implicit Kirk-Noor, implicit Kirk-Ishikawa and implicit Kirk-Mann iterations for the same class of mapping under consideration.

Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space and D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ be a selfmap of D, let $x_0\in D$ . Then, the sequence ${\left\{x_n\right\}}_{n=0}^{\infty }$ defined by

$\begin{array}{l}{x}_{n+1}={\alpha }_{n,0}{x}_n^1+{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{T}^i{x}_{n+1}},{\displaystyle {\sum }_{i=0}^{q_1}{\alpha }_{n,i}}=1\\ x_n^j={\beta }_{n,0}^j{x}_n^{j+1}+{\displaystyle {\sum }_{i=1}^{q_{j+1}}{\beta }_{n,i}^j{T}^i{x}_n^j},{\displaystyle {\sum }_{i=0}^{q_{j+1}}{\beta }_{n,i}^j}=1,j=1,2,\cdots ,k-2,\\ x_n^{k-1}={\beta }_{n,0}^{k-1}{x}_n+{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{k-1}{T}^i{x}_n^{k-1}},{\displaystyle {\sum }_{i=0}^{q_k}{\beta }_{n,i}^{k-1}}=1,k\ge 2,n\ge 1\end{array}\}$ (2)

where $q_1\ge q_2\ge q_3\ge \cdots \ge q_k$ , for each j, ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\beta }_{n\mathrm{,}i}^j\ge 0$ , ${\beta }_{n\mathrm{,0}}^j\ne 0$ , for each j, ${\alpha }_{n\mathrm{,}i}\mathrm{,}{\beta }_{n\mathrm{,}i}^j\in \left[\mathrm{0,1}\right]$ for each j and $q_1$ , $q_j$ are fixed integers (for each j). (2) is called implicit Kirk-multistep iterations.

Equation (2) serves as a general formula for obtaining other implicit Kirk-type iterations. Infact, if $k=3$ in (2), we obtain a three step (implicit Kirk-Noor) iteration as follows:

$\begin{array}{l}{x}_{n+1}={\alpha }_{n,0}{x}_n^1+{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{T}^i{x}_{n+1}},{\displaystyle {\sum }_{i=0}^{q_1}{\alpha }_{n,i}}=1\\ x_n^1={\beta }_{n,0}^1{x}_n^2+{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^1{T}^i{x}_n^1},{\displaystyle {\sum }_{i=0}^{q_2}{\beta }_{n,i}^1}=1,\\ x_n^2={\beta }_{n,0}^2{x}_n+{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^2{T}^i{x}_n^2},{\displaystyle {\sum }_{i=0}^{q_3}{\beta }_{n,i}^2}=1,\end{array}\}$ (3)

where $q_1\ge q_2\ge q_3$ , ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\beta }_{n\mathrm{,}i}^1\ge 0$ , ${\beta }_{n\mathrm{,0}}^1\ne 0$ , ${\beta }_{n\mathrm{,}i}^2\ge 0$ , ${\beta }_{n\mathrm{,0}}^2\ne 0$ , ${\alpha }_{n\mathrm{,}i}\mathrm{,}{\beta }_{n\mathrm{,}i}^1\mathrm{,}{\beta }_{n\mathrm{,}i}^2\in \left[\mathrm{0,1}\right]$ and $q_1\mathrm{,}{q}_2$ and $q_3$ are fixed integers.

If $k=2$ in (2), we obtain a two step (implicit Kirk-Ishikawa) iteration as follows:

$\begin{array}{l}{x}_{n+1}={\alpha }_{n,0}{x}_n^1+{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{T}^i{x}_{n+1}},{\displaystyle {\sum }_{i=0}^{q_1}{\alpha }_{n,i}}=1\\ x_n^1={\beta }_{n,0}^1{x}_n+{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^1{T}^i{x}_n^1},{\displaystyle {\sum }_{i=0}^{q_3}{\beta }_{n,i}^1}=1,\end{array}\}$ (4)

where $q_1\ge q_2$ , ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\beta }_{n\mathrm{,}i}^1\ge 0$ , ${\beta }_{n\mathrm{,0}}^1\ne 0$ , ${\alpha }_{n\mathrm{,}i}\mathrm{,}{\beta }_{n\mathrm{,}i}^1\in \left[\mathrm{0,1}\right]$ and $q_1$ and $q_2$ are fixed integers.

Finally, if $k=2$ and $q_2=0$ in (2), we obtain a one step (implicit Kirk-Mann) iteration as follows:

$x_{n+1}={\alpha }_{n,0}{x}_n^1+{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{T}^i{x}_{n+1},{\displaystyle \underset{i=0}{\overset{q_1}{\sum }}}{\alpha }_{n,i}=1,$ (5)

where ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\alpha }_{n\mathrm{,}i}\in \left[\mathrm{0,1}\right]$ and $q_1$ is a fixed integer.

Equations (3)-(5) will be rewritten in the following forms to help us prove our equivalence result:

Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space and D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ be a selfmap of D, let $y_0\in D$ . Then, the implicit Kirk-Noor scheme is a sequence ${\left\{y_n\right\}}_{n=0}^{\infty }$ defined by

$\begin{array}{l}{y}_{n+1}={\alpha }_{n,0}{y}_n^1+{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{T}^i{y}_{n+1}},{\displaystyle {\sum }_{i=0}^{q_1}{\alpha }_{n,i}}=1\\ y_n^1={\beta }_{n,0}^1{y}_n^2+{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^1{T}^i{y}_n^1},{\displaystyle {\sum }_{i=0}^{q_2}{\beta }_{n,i}^1}=1\\ y_n^2={\beta }_{n,0}^2{y}_n+{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^2{T}^i{x}_n^2},{\displaystyle {\sum }_{i=0}^{q_3}{\beta }_{n,i}^2}=1\end{array}\}$ (6)

where $q_1\ge q_2\ge q_3$ , ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\beta }_{n\mathrm{,}i}^1\ge 0$ , ${\beta }_{n\mathrm{,0}}^1\ne 0$ , ${\beta }_{n\mathrm{,}i}^2\ge 0$ , ${\beta }_{n\mathrm{,0}}^2\ne 0$ , ${\alpha }_{n\mathrm{,}i}\mathrm{,}{\beta }_{n\mathrm{,}i}^1\mathrm{,}{\beta }_{n\mathrm{,}i}^2\in \left[\mathrm{0,1}\right]$ and $q_1\mathrm{,}{q}_2$ and $q_3$ are fixed integers.

Also, for $z_0\in D$ , the two step (implicit Kirk-Ishikawa) iteration scheme is a sequence ${\left\{z_n\right\}}_{n=0}^{\infty }$ defined as follows:

$\begin{array}{l}{z}_{n+1}={\alpha }_{n,0}{z}_n^1+{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{T}^i{z}_{n+1}},{\displaystyle {\sum }_{i=0}^{q_1}{\alpha }_{n,i}}=1\\ z_n^1={\beta }_{n,0}^1{z}_n+{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^1{T}^i{z}_n^1},{\displaystyle {\sum }_{i=0}^{q_2}{\beta }_{n,i}^1}=1\end{array}\}$ (7)

where $q_1\ge q_2$ , ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\beta }_{n\mathrm{,}i}^1\ge 0$ , ${\beta }_{n\mathrm{,0}}^1\ne 0$ , ${\alpha }_{n\mathrm{,}i}\mathrm{,}{\beta }_{n\mathrm{,}i}^1\in \left[\mathrm{0,1}\right]$ and $q_1$ and $q_2$ are fixed integers.

Finally, for $u_0\in D$ , the implicit Kirk-Mann iteration scheme is a sequence ${\left\{u_n\right\}}_{n=0}^{\infty }$ defined by:

$u_{n+1}={\alpha }_{n,0}{u}_n^1+{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{T}^i{u}_{n+1},{\displaystyle \underset{i=0}{\overset{q_1}{\sum }}}{\alpha }_{n,i}=1$ (8)

where ${\alpha }_{n\mathrm{,}i}\ge 0$ , ${\alpha }_{n\mathrm{,0}}\ne 0$ , ${\alpha }_{n\mathrm{,}i}\in \left[\mathrm{0,1}\right]$ and $q_1$ is a fixed integer. We shall now consider some of the contractive mappings useful in proving our main results.

Let E be a normed linear space and D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ be a selfmap of D. There exists a real number $a\in \left[\mathrm{0,1}\right)$ and all $x\mathrm{,}y\in D$ such that

$\Vert x-Ty\Vert \le a\Vert x-y\Vert$ (9)

Zamfirescu [6] , discussed mappings T satisfying the following contractive condition:

$\Vert Tx-Ty\Vert \le \delta \Vert x-y\Vert +2\delta \Vert x-Tx\Vert$ (10)

where $\delta \in \left[\mathrm{0,1}\right)$ . Inequality (10) becomes (9) if x is a fixed point of T.

Osilike [7] proved several stability results which are generalizations and extensions of most of the results of Rhoades [8] using the following contractive definition: for each $x\mathrm{,}y\in E$ , there exist $a\in \left[\mathrm{0,1}\right)$ and $L\ge 0$ such that

$\Vert Tx-Ty\Vert \le a\Vert x-y\Vert +L\Vert x-Tx\Vert$ (11)

In 2003, Imoru and Olatinwo [9] proved some stability results using the following general contractive definition: for each $x\mathrm{,}y\in E$ , there exists $\delta \in \left[\mathrm{0,1}\right)$ and a monotone increasing function $\phi \mathrm{<mo>\; :\; </mo>}{R}^{+}\to R^{+}$ with $\phi \left(0\right)=0$ such that

$\Vert Tx-Ty\Vert \le \delta \Vert x-y\Vert +\phi \left(\Vert x-Tx\Vert \right)\mathrm{.}$ (12)

In 2010, Bosede and Rhoades [5] , made an assumption implied by (9) and one which attempted to put an end to all generalizations of the form (12). That is if $x=p$ (is a fixed point) then (12) becomes inequality (9).

In 2014, Chidume and Olaleru [10] gave several examples to show that the class of mappings satisfying (9) is more general than that of (10), (11) and (12) provided the fixed point exists.

We shall need the following lemma in proving our result.

Lemma 1.2 [11] : Let $\delta$ be a real number satisfying $0\le \delta <1$ and ${\left\{{ϵ}_n\right\}}_{n=0}^{\infty }$ a sequence of positive numbers such that ${\lim }_{n\to \infty }{ϵ}_n=0$ , then for any sequence of positive numbers ${\left\{u_n\right\}}_{n=0}^{\infty }$ satisfying

$u_{n+1}\le \delta u_n+{ϵ}_n;n=0,1,2,\cdots$ (13)

we have ${\lim }_{n\to \infty }{u}_n=0$ .

Lemma 1.3 [12] : Let ${\left\{a_n\right\}}_{n=0}^{\infty }$ and ${\left\{e_n\right\}}_{n=0}^{\infty }$ be nonnegative real sequences satisfying the following inequality $a_{n+1}\le \left(1-{\lambda }_n\right)a_n+e_n$ , where ${\lambda }_n\in \left(\mathrm{0,1}\right)$ , for all $n\ge n_0$ , ${\displaystyle {\sum }_{n=0}^{\infty }}{\lambda }_n=\infty$ and $e_n=o\left({\lambda }_n\right)$ . Then ${\lim }_{n\to \infty }{a}_n=0$

2. Main Result

Theorem 2.1. Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space, D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ , a self map satisfying the inequality:

$\Vert T^{i}x-Tp\Vert \le a^i\Vert x-p\Vert$ (14)

where $a^i\in \left[\mathrm{0,1}\right)$ and $p\in F\left(T\right)$ . For $x_0\in D$ , let $\left\{x_n\right\}$ be the implicit Kirk-multistep iteration scheme defined by (2) with ${\displaystyle {\sum }_{n=1}^{\infty }}\left(1-{\alpha }_{n,0}\right)=\infty$ . Then

i) the fixed point p of T defined by (14) is unique;

ii) the implicit Kirk-multistep iteration scheme converges strongly to the unique fixed point p of T.

Proof:

i) The first thing is to establish that the mapping T satisfying the contractive condition (14) has a unique fixed point.

Suppose there exist $p_1\mathrm{,}{p}_2\in F_T$ , and that $p_1\ne p_2$ , with $\Vert p_1-p_2\Vert >0$ , then,

$\left(1-a^i\right)\Vert p_1-p_2\Vert \le 0.$ (15)

Since $a^i\in \left[\mathrm{0,1}\right)$ , then $1-a^i>0$ and $\Vert p_1-p_2\Vert \le 0$ . Since norm is nonnegative we have that $\Vert p_1-p_2\Vert =0$ . That is, $p_1=p_2=p$ (say). Thus, T has a unique fixed point p.

ii) Next, we prove that (2) converges strongly to p. In veiw of (2) and (14),

$\begin{array}{c}\Vert x_{n+1}-p\Vert \le {\alpha }_{n,0}\Vert x_n^{\left(1\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}\Vert T^i{x}_{n+1}-T^{i}p\Vert \\ \le {\alpha }_{n,0}\Vert x_n^{\left(1\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}\left[a^i\Vert x_{n+1}-p\Vert \right]\\ \le \frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\Vert x_n^{\left(1\right)}-p\Vert \end{array}$ (16)

Also, using (2) and (14), we have:

$\begin{array}{c}\Vert x_n^{\left(1\right)}-p\Vert \le {\beta }_{n,0}^{\left(1\right)}\Vert x_n^{\left(2\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert T^i{x}_n^{\left(1\right)}-T^{i}p\Vert \\ \le {\beta }_{n,0}^{\left(1\right)}\Vert x_n^{\left(2\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\left[a^i\Vert x_n^{\left(1\right)}-p\Vert \right]\\ \le \frac{{\beta }_{n,0}^{\left(1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert x_n^{\left(2\right)}-p\Vert \end{array}$ (17)

Again, using (2) and (14), we have:

$\begin{array}{c}\Vert x_n^{\left(2\right)}-p\Vert \le {\beta }_{n,0}^{\left(2\right)}\Vert x_n^{\left(3\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_3}{\sum }}}{\beta }_{n,i}^{\left(2\right)}\Vert T^i{x}_n^2-T^{i}p\Vert \\ \le {\beta }_{n,0}^{\left(2\right)}\Vert x_n^{\left(3\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_3}{\sum }}}{\beta }_{n,i}^{(2)}\left[a^i\Vert x_n^{\left(2\right)}-p\Vert \right]\\ \le \frac{{\beta }_{n,0}^{\left(2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}{a}^i}}\Vert x_n^{\left(3\right)}-p\Vert \end{array}$ (18)

Continuing the process using (2) and (14), we have

$\begin{array}{c}\Vert x_n^{\left(k-2\right)}-p\Vert \le {\beta }_{n,0}^{\left(k-2\right)}\Vert x_n^{\left(k-1\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_{k-1}}{\sum }}}{\beta }_{n,i}^{\left(k-2\right)}\Vert T^i{x}_n^{k-2}-T^{i}p\Vert \\ \le {\beta }_{n,0}^{\left(k-2\right)}\Vert x_n^{\left(k-1\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_{k-1}}{\sum }}}{\beta }_{n,i}^{\left(k-2\right)}\left[a^i\Vert x_n^{\left(k-2\right)}-p\Vert \right]\\ \le \frac{{\beta }_{n,0}^{\left(k-2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\Vert x_n^{\left(k-1\right)}-p\Vert \end{array}$ (19)

Finally, using (2) and (14) for $\left(k-1\right)$ , we have:

$\begin{array}{c}\Vert x_n^{\left(k-1\right)}-p\Vert \le {\beta }_{n,0}^{\left(k\right)}\Vert x_n^{\left(k\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_k}{\sum }}}{\beta }_{n,i}^{\left(k-1\right)}\Vert T^i{x}_n^{k-1}-T^{i}p\Vert \\ \le {\beta }_{n,0}^{\left(k-1\right)}\Vert x_n^{\left(k\right)}-p\Vert +{\displaystyle \underset{i=1}{\overset{q_k}{\sum }}}{\beta }_{n,i}^{\left(k-1\right)}\left[a^i\Vert x_n^{\left(k-1\right)}-p\Vert \right]\\ \le \frac{{\beta }_{n,0}^{\left(k-1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\Vert x_n^{\left(k\right)}-p\Vert \end{array}$ (20)

Substituting (20) in (19), (19) in (18), (18) in (17) and (17) in (16), we obtain:

$\begin{array}{l}\Vert x_{n+1}-p\Vert \le \left[\frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\right]\left[\frac{{\beta }_{n,0}^{\left(1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\right]\left[\frac{{\beta }_{n,0}^{\left(2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}{a}^i}}\right]\cdots \\ \cdot \left[\frac{{\beta }_{n,0}^{\left(k-2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\right]\left[\frac{{\beta }_{n,0}^{\left(k-1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\right]\Vert x_n^{\left(k\right)}-p\Vert \end{array}$ (21)

Note that

$1-\frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}=\frac{1-\left[{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}+{\alpha }_{n,0}\right]}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\ge 1-\left[{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i+{\alpha }_{n,0}\right]$ (22)

hence

$\frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\le {\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i+{\alpha }_{n,0}$

Let $a^i<a<1$ , then

${\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i+{\alpha }_{n,0}\le \left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}$ (23)

That is,

$\frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\le \left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}$ (24)

Therefore,

$\begin{array}{c}\Vert x_{n+1}-p\Vert \le \left[\left(1-{\alpha }_{n\mathrm{,0}}\right)a+{\alpha }_{n\mathrm{,0}}\right]\left[\left(1-{\beta }_{n\mathrm{,0}}^{\left(1\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(1\right)}\right]\left[\left(1-{\beta }_{n\mathrm{,0}}^{\left(2\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(2\right)}\right]\cdots \\ \cdot \left[\left(1-{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}\right]\left[\left(1-{\beta }_{n\mathrm{,0}}^{\left(k-1\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(k-1\right)}\right]\Vert x_n-p\Vert \\ \le \left[1-\left(1-{\alpha }_{n\mathrm{,0}}\right)\left(1-a\right)\right]\Vert x_n-p\Vert \end{array}$ (25)

Hence, using Lemma 1.2 in (25), then ${{\displaystyle \lim }}_{n\to \infty }\Vert x_n-p\Vert =0$ This ends the proof.

Theorem 2.1 leads to the following corollary:

Corollary 2.2. Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space, D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ , with $p\in F\left(T\right)$ , such that:

$\Vert T^{i}x-p\Vert \le a^i\Vert x-p\Vert$ (26)

where $a^i\in \left[\mathrm{0,1}\right)$ . For $y_0=z_0=u_0\in D$ , let $\left\{y_n\right\}$ $\left\{z_n\right\}$ $\left\{u_n\right\}$ be the implicit Kirk-Noor, implicit Kirk-Ishikawa and implicit Kirk-Mann iteration scheme respectively defined by (6), (7) and (8) with ${\displaystyle {\sum }_{n=1}^{\infty }}\left(1-{\alpha }_{n,0}\right)=\infty$ , $\left(1-{\beta }_{n,0}^1\right)=\infty$ , $\left(1-{\beta }_{n,0}^2\right)=\infty$ . Then

i) T defined by (26) has a unique fixed point p;

ii) $\left\{y_n\right\}$ (6) converges strongly to the unique fixed point p of T;

iii) $\left\{z_n\right\}$ (7) converges strongly to the unique fixed point p of T;

iv) $\left\{u_n\right\}$ (8) converges strongly to the unique fixed point p of T.

Theorem 2.3. Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space, D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ an operator satisfying

$\Vert T^{i}x-Tp\Vert \le a^i\Vert x-p\Vert$ (27)

where $a^i\in \left[\mathrm{0,1}\right)$ and $p\in F\left(T\right)$ . If $u_0=x_0\in D$ , then the following are equivalent: the

i) implicit Kirk-Mann iterative scheme ${\left\{u_n\right\}}_{n=0}^{\infty }$ (8) converges strongly to p;

ii) implicit Kirk-multistep iterative scheme ${\left\{x_n\right\}}_{n=0}^{\infty }$ (2) converges strongly to p.

Proof:

We prove that (i) Þ (ii).

Assume ${\lim }_{n\to \infty }{u}_n=p$ , then using (8), (2) and (27), we have

$\begin{array}{c}\Vert u_{n+1}-x_{n+1}\Vert =\Vert {\alpha }_{n,0}\left(u_n-x_n^{\left(1\right)}\right)+{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{T}^i{u}_{n+1}-{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{T}^i{x}_{n+1}\Vert \\ \le {\alpha }_{n,0}\Vert u_n-x_n^{\left(1\right)}\Vert +{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}\Vert T^i{u}_{n+1}-T^i{x}_{n+1}\Vert .\end{array}$ (28)

Using condition (27) in (28), we have

$\begin{array}{c}\Vert u_{n+1}-x_{n+1}\Vert \le {\alpha }_{n,0}\Vert u_n-x_n^{\left(1\right)}\Vert +{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i\Vert u_{n+1}-x_{n+1}\Vert \\ \le \frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\Vert u_n-x_n^{\left(1\right)}\Vert \end{array}$ (29)

From (29),

$\begin{array}{c}\Vert u_n-x_n^{\left(1\right)}\Vert \le {\beta }_{n,0}^{\left(1\right)}\Vert u_n-x_n^{\left(2\right)}\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert u_n-T^i{u}_n+T^i{u}_n-T^i{x}_n^{\left(1\right)}\Vert \\ \le {\beta }_{n,0}^{\left(1\right)}\Vert u_n-x_n^{\left(2\right)}\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert u_n-T^i{u}_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert T^i{u}_n-T^i{x}_n^{\left(1\right)}\Vert \\ \le {\beta }_{n,0}^{\left(1\right)}\Vert u_n-x_n^{\left(2\right)}\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert u_n-T^i{u}_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{(1)}{a}^i\Vert u_n-x_n^{\left(1\right)}\Vert \end{array}$ (30)

From (30),

$\Vert u_n-x_n^{\left(1\right)}\Vert \le \frac{{\beta }_{n,0}^{\left(1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert u_n-x_n^{\left(2\right)}\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert u_n-T^i{u}_n\Vert$ (31)

But from (31),

$\Vert u_n-T^i{u}_n\Vert =\Vert u_n-p+Tp-T^i{u}_n\Vert \le \Vert u_n-p\Vert +\Vert Tp-T^i{u}_n\Vert$ (32)

Applying condition (27) on (31), we get

$\Vert u_n-T^i{u}_n\Vert \le \left(1+a^i\right)\Vert u_n-p\Vert$ (33)

Using (33) in (31), we have

$\Vert u_n-x_n^{\left(1\right)}\Vert \le \frac{{\beta }_{n,0}^{\left(1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert u_n-x_n^{\left(2\right)}\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\left(1+a^i\right)\Vert u_n-p\Vert$ (34)

Similarly,

$\Vert u_n-x_n^{\left(2\right)}\Vert \le \frac{{\beta }_{n,0}^{\left(2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}{a}^i}}\Vert u_n-x_n^{\left(3\right)}\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}{a}^i}}\left(1+a^i\right)\Vert u_n-p\Vert$ (35)

Also

$\Vert u_n-x_n^{\left(3\right)}\Vert \le \frac{{\beta }_{n,0}^{\left(3\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_4}{\beta }_{n,i}^{\left(3\right)}{a}^i}}\Vert u_n-x_n^{\left(4\right)}\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_4}{\beta }_{n,i}^{\left(3\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_4}{\beta }_{n,i}^{\left(3\right)}{a}^i}}\left(1+a^i\right)\Vert u_n-p\Vert$ (36)

Continuing (k − 2) times, we have

$\begin{array}{l}\Vert u_n-x_n^{\left(k-2\right)}\Vert \le \frac{{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n\mathrm{,}i}^{\left(k-2\right)}{a}^i}}\Vert u_n-x_n^{\left(k-1\right)}\Vert \\ +\frac{{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n\mathrm{,}i}^{\left(k-2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n\mathrm{,}i}^{\left(k-2\right)}{a}^i}}\left(1+a^i\right)\Vert u_n-p\Vert \end{array}$ (37)

Moving a step more, we have

$\Vert u_n-x_n^{\left(k-1\right)}\Vert \le \frac{{\beta }_{n,0}^{\left(k-1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\Vert u_n-x_n^{\left(k\right)}\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\left(1+a^i\right)\Vert u_n-p\Vert$ (38)

Substituting (35) into (34), (34) into (33), (33) into (32) and (32) into (31) respectively, we obtain

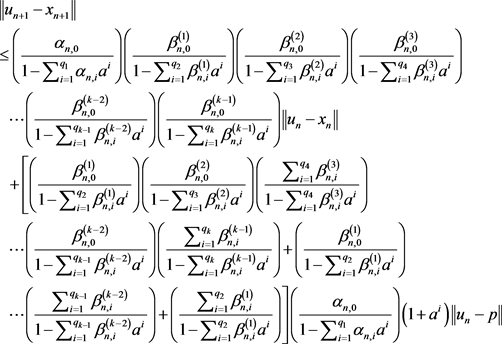(39)

Recall that

$\frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\le {\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i+{\alpha }_{n,0}$ (40)

Let $a^i<a<1$ , then

${\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i+{\alpha }_{n,0}\le \left[\left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}\right]$ (41)

Using (36), (37) in (38), we have

$\begin{array}{l}\Vert u_{n+1}-x_{n+1}\Vert \\ \le \left[\left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}\right]\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(2\right)}\right)a+{\beta }_{n,0}^{\left(2\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(3\right)}\right)a+{\beta }_{n,0}^{\left(3\right)}\right]\\ \cdots \left[\left(1-{\beta }_{n,0}^{\left(k-2\right)}\right)a+{\beta }_{n,0}^{\left(k-2\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(k-1\right)}\right)a+{\beta }_{n,0}^{\left(k-1\right)}\right]\Vert u_n-x_n\Vert \\ +\{\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(2\right)}\right)a+{\beta }_{n,0}^{\left(2\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(3\right)}\right)a+{\beta }_{n,0}^{\left(3\right)}\right]\underset{\begin{array}{l}\\ \end{array}}{\overset{}{}}\\ \cdots \left[\left(1-{\beta }_{n,0}^{\left(k-2\right)}\right)a+{\beta }_{n,0}^{\left(k-2\right)}\right]\left[\frac{{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\right]+\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\end{array}$

$\begin{array}{l}\cdots \left[\frac{{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\right]+\left[\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\right]\}\left[\left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}\right]\left(1+a^i\right)\Vert u_n-p\Vert \\ \le \left[1-\left(1-{\alpha }_{n,0}\right)\left(1-a\right)\right]\Vert u_n-x_n\Vert +\{\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(2\right)}\right)a+{\beta }_{n,0}^{\left(2\right)}\right]\underset{\begin{array}{l}\\ \end{array}}{\overset{}{}}\\ \cdot \left[\left(1-{\beta }_{n,0}^{\left(3\right)}\right)a+{\beta }_{n,0}^{\left(3\right)}\right]\cdots \left[\left(1-{\beta }_{n,0}^{\left(k-2\right)}\right)a+{\beta }_{n,0}^{\left(k-2\right)}\right]\left[\frac{{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\right]\\ +\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\cdots \left[\frac{{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\right]+\left[\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\right]\}\\ \cdot \left[\left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}\right]\left(1+a^i\right)\Vert u_n-p\Vert \end{array}$ (42)

Let ${\lambda }_n=\left(1-{\alpha }_{n\mathrm{,0}}\right)\left(1-a\right)$ and

$\begin{array}{c}{e}_n=\{\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(2\right)}\right)a+{\beta }_{n,0}^{\left(2\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(3\right)}\right)a+{\beta }_{n,0}^{\left(3\right)}\right]\underset{\begin{array}{l}\\ \end{array}}{\overset{}{}}\\ \cdots \left[\left(1-{\beta }_{n,0}^{\left(k-2\right)}\right)a+{\beta }_{n,0}^{\left(k-2\right)}\right]\left[\frac{{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n\mathrm{,}i}^{\left(k-1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n\mathrm{,}i}^{\left(k-1\right)}{a}^i}}\right]\\ +\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\cdots \left[\frac{{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n\mathrm{,}i}^{\left(k-2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n\mathrm{,}i}^{\left(k-2\right)}{a}^i}}\right]+\left[\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n\mathrm{,}i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n\mathrm{,}i}^{\left(1\right)}{a}^i}}\right]\}\\ \cdot \left[\left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}\right]\left(1+a^i\right)\Vert u_n-p\Vert \end{array}$ (43)

Replacing (40) in (39), we have

$\Vert u_{n+1}-x_{n+1}\Vert \le \left(1-{\lambda }_n\right)\Vert u_n-x_n\Vert +e_n$ (44)

By Lemma 1.3 in (41), it follows that

$\underset{n\to \infty }{\lim }\Vert u_n-x_n\Vert =0$ (45)

Since by the assumption, ${\lim }_{n\to \infty }{u}_n=p$ ,

then $\Vert x_n-p\Vert \le \Vert u_n-x_n\Vert +\Vert u_n-p\Vert \to 0$ as $n\to \infty$

Hence ${\lim }_{n\to \infty }{x}_n=p$ .

Next is to show that (ii) implies (i).

Assume, ${\lim }_{n\to \infty }{x}_n=p$ , then using (2), (8) and (27), we have

$\begin{array}{c}\Vert x_{n+1}-u_{n+1}\Vert \le \Vert {\alpha }_{n,0}\left(x_n^{\left(1\right)}-u_n\right)+{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}\left(T^i{x}_{n+1}-T^i{u}_{n+1}\right)\Vert \\ \le {\alpha }_{n,0}\Vert x_n^{\left(1\right)}-u_n\Vert +{\displaystyle \underset{i=1}{\overset{q_1}{\sum }}}{\alpha }_{n,i}{a}^i\Vert T^i{x}_{n+1}-T^i{u}_{n+1}\Vert \\ \le \frac{{\alpha }_{n,0}}{1-{\displaystyle {\sum }_{i=1}^{q_1}{\alpha }_{n,i}{a}^i}}\Vert x_n^{\left(1\right)}-u_n\Vert \end{array}$ (46)

$\begin{array}{c}\Vert x_n^{\left(1\right)}-u_n\Vert \le \Vert {\beta }_{n,0}^{\left(1\right)}\left(x_n^{\left(2\right)}-u_n\right)+{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\left(T^i{x}_n^{\left(1\right)}-u_n\right)\Vert \\ \le {\beta }_{n,0}^{\left(1\right)}\Vert x_n^{\left(2\right)}-u_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\parallel T^i{x}_n^{\left(1\right)}-T^i{u}_n+T^i{u}_n-u_n\parallel \\ \le {\beta }_{n,0}^{\left(1\right)}\Vert x_n^{\left(2\right)}-u_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert T^i{x}_n^{\left(1\right)}-T^i{u}_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert T^i{u}_n-u_n\Vert \\ \le {\beta }_{n,0}^{\left(1\right)}\Vert x_n^{\left(2\right)}-u_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}{a}^i\Vert x_n^{\left(1\right)}-u_n\Vert +{\displaystyle \underset{i=1}{\overset{q_2}{\sum }}}{\beta }_{n,i}^{\left(1\right)}\Vert T^i{u}_n-u_n\Vert \end{array}$ (47)

By simplifying (42), we obtain

$\Vert x_n^{\left(1\right)}-u_n\Vert \le \frac{{\beta }_{n,0}^{\left(1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert x_n^{\left(2\right)}-u_n\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert T^i{u}_n-u_n\Vert$ (48)

But,

$\begin{array}{c}\Vert T^i{u}_n-u_n\Vert \le \Vert T^i{u}_n-T^{i}p+p-u_n\Vert \\ \le \Vert T^i{u}_n-T^{i}p\Vert +\Vert p-u_n\Vert \\ \le a^i\Vert u_n-p\Vert +\Vert u_n-p\Vert \\ \le \left(a^i+1\right)\Vert u_n-p\Vert \end{array}$ (49)

Substituting (44) in (43), we have

$\Vert x_n^{\left(1\right)}-u_n\Vert \le \frac{{\beta }_{n,0}^{\left(1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\Vert x_n^{\left(2\right)}-u_n\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\left(a^i+1\right)\Vert u_n-p\Vert$ (50)

Similarly,

$\Vert x_n^{\left(2\right)}-u_n\Vert \le \frac{{\beta }_{n\mathrm{,0}}^{\left(2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}{a}^i}}\Vert x_n^{\left(3\right)}-u_n\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_3}{\beta }_{n,i}^{\left(2\right)}{a}^i}}\left(a^i+1\right)\Vert u_n-p\Vert$ (51)

Also,

$\Vert x_n^{\left(3\right)}-u_n\Vert \le \frac{{\beta }_{n,0}^{\left(3\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_4}{\beta }_{n,i}^{\left(3\right)}{a}^i}}\Vert x_n^{\left(4\right)}-u_n\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_4}{\beta }_{n,i}^{\left(3\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_4}{\beta }_{n,i}^{\left(3\right)}{a}^i}}\left(a^i+1\right)\Vert u_n-p\Vert$ (52)

Continuing the process upto (k − 2), we have

$\Vert x_n^{\left(k-2\right)}-u_n\Vert \le \frac{{\beta }_{n,0}^{\left(k-2\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\Vert x_n^{\left(k-1\right)}-u_n\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\left(a^i+1\right)\Vert u_n-p\Vert$ (53)

For (k − 1), we get

$\Vert x_n^{\left(k-1\right)}-u_n\Vert \le \frac{{\beta }_{n,0}^{\left(k-1\right)}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\Vert x_n-u_n\Vert +\frac{{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\left(a^i+1\right)\Vert u_n-p\Vert$ (54)

Substituting accordingly from (41) to (48), we get

$\begin{array}{l}\Vert x_{n+1}-u_{n+1}\Vert \\ \le \left[\left(1-{\alpha }_{n\mathrm{,0}}\right)a+{\alpha }_{n\mathrm{,0}}\right]\left[\left(1-{\beta }_{n,0}^{\left(1\right)}\right)a+{\beta }_{n,0}^{\left(1\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(2\right)}\right)a+{\beta }_{n,0}^{\left(2\right)}\right]\left[\left(1-{\beta }_{n,0}^{\left(3\right)}\right)a+{\beta }_{n,0}^{\left(3\right)}\right]\\ \cdots \left[\left(1-{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}\right]\left[\left(1-{\beta }_{n\mathrm{,0}}^{\left(k-1\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(k-1\right)}\right]\Vert x_n-u_n\Vert \end{array}$

$\begin{array}{l}+[\left(\left(1-{\beta }_{n\mathrm{,0}}^{\left(1\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(1\right)}\right)\left(\left(1-{\beta }_{n\mathrm{,0}}^{\left(2\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(2\right)}\right)\cdots \left(\left(1-{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(k-2\right)}\right)\underset{\begin{array}{l}\\ \end{array}}{\overset{}{}}\\ \cdot \left(\frac{{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_k}{\beta }_{n,i}^{\left(k-1\right)}{a}^i}}\right)+\left(\left(1-{\beta }_{n\mathrm{,0}}^{\left(1\right)}\right)a+{\beta }_{n\mathrm{,0}}^{\left(1\right)}\right)\cdots \left(\frac{{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_{k-1}}{\beta }_{n,i}^{\left(k-2\right)}{a}^i}}\right)\\ +\left(\frac{{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}}}{1-{\displaystyle {\sum }_{i=1}^{q_2}{\beta }_{n,i}^{\left(1\right)}{a}^i}}\right)]\left(\left(1-{\alpha }_{n\mathrm{,0}}\right)a+{\alpha }_{n\mathrm{,0}}\right)\left(a^i+1\right)\Vert u_n-p\Vert \end{array}$ (55)

(50) can be written as:

$\begin{array}{c}\Vert x_{n+1}-u_{n+1}\Vert \le \left[1-\left(1-{\alpha }_{n\mathrm{,0}}\right)\left(1-a\right)\right]\Vert x_n-u_n\Vert \\ +\left[1-\left(1-{\alpha }_{n\mathrm{,0}}\right)a+{\alpha }_{n\mathrm{,0}}\right]\left(a^i+1\right)\Vert u_n-p\Vert \end{array}$ (56)

Let

${\lambda }_n=\left(1-{\alpha }_{n,0}\right)\left(1-a\right)e_n=\left[1-\left(1-{\alpha }_{n,0}\right)a+{\alpha }_{n,0}\right]\left(a^i+1\right)\Vert u_n-p\Vert$

Therefore,

$\Vert x_{n+1}-u_{n+1}\Vert \le \left(1-{\lambda }_n\right)\Vert x_n-u_n\Vert +e_n$ (57)

It follows from Lemma 1.3 that: ${\lim }_{n\to \infty }\Vert x_n-u_n\Vert =0$

Since by assumption, ${\lim }_{n\to \infty }{u}_n=p$ Then, $\Vert u_n-p\Vert \le \Vert x_n-u_n\Vert +\Vert x_n-p\Vert \to \mathrm{0,}n\to \infty$ .

This implies that ${\lim }_{n\to \infty }{u}_n=p$ .

Since (i) → (ii) and (ii) → (i), it shows that the convergence of implicit Kirk-Mann iterative scheme (8) is equivalent to the convergence of implicit Kirk-multistep iterative scheme (2) when applied to the general class of map (14). This ends the proof.

Theorem 2.3 leads to the following Corollaries:

Corollary 2.4. Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space, D a non-empty, convex, closed subset of E and $T\mathrm{<mo>\; :\; </mo>}D\to D$ , with $p\in F\left(T\right)$ , satisfying

$\Vert T^i-p\Vert \le a^i\Vert x-p\Vert$ (58)

where $a^i\in \left[\mathrm{0,1}\right)$ . If $u_0=z_0=y_0\in D$ , then the following are equivalent: the

a) (i) implicit Kirk-Mann iterative scheme ${\left\{u_n\right\}}_{n=0}^{\infty }$ (8) converges strongly to p;

(ii) implicit Kirk-Ishikawa iterative scheme ${\left\{z_n\right\}}_{n=0}^{\infty }$ (7) converges strongly to p.

b) (i) implicit Kirk-Mann iterative scheme ${\left\{u_n\right\}}_{n=0}^{\infty }$ (8) converges strongly to p;

(ii) implicit Kirk-Noor iterative scheme ${\left\{y_n\right\}}_{n=0}^{\infty }$ (6) converges strongly to p.

Proof. The proof of Corollary 2.4 is similar to that of Theorem 2.3.This ends the proof.

Corollary 2.5. Let $\left(E\mathrm{,}\Vert \mathrm{.}\Vert \right)$ be a normed linear space, D a non-empty, convex, closed subset of E and an operator satisfying

(59)

where. If, then the following are equivalent:

i) implicit Kirk-Mann iterative scheme (8) converges strongly to p;

ii) implicit Kirk-Ishikawa iterative scheme 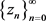(7) converges strongly to p;

iii) implicit Kirk-Noor iterative scheme (6) converges strongly to p;

iv) implicit Kirk-multistep iterative scheme (2) converges strongly to p.

3. Numerical Examples

In this section, we use some examples to demonstrate the equivalence of convergence between implicit Kirk-multistep (IKMST) iterative scheme (2) and other implicit Kirk-type [implicit Kirk-Noor (IKN)(6), implicit Kirk-Ishikawa (IKI)(7) and implicit Kirk-Mann (IKM)(8)] iterative schemes with the help of computer programs in PYTHON 2.5.4. We shall consider our results for increasing and decreasing functions. The results are shown in Table 1 and Table 2.

3.1. Example of Increasing Function (See 5.12 of [4] )

Let be defined by. Then f is an increasing function with fixed point. By taking initial approximation as (mid point of x and y) and , (for), , , , for all the iterative schemes. The equivalence of convergence results to the fixed point are shown in Table 1.

3.2. Example of Decreasing Function (See 5.11 of [4] )

Let be defined by. Then f is a decreasing function with fixed point. By taking initial approximation as and, (for ), , , , for all the iterative schemes. The equivalence of convergence results to the fixed point are shown in Table 2.

4. Remark

i) From Table 1, it is observed that for increasing function, the

convergence of implicit Kirk-multistep iterative scheme (2) to the fixed point 6.000000 is equivalent to the convergence of other implicit Kirk-type [implicit Kirk-Noor (IKN) (6), implicit Kirk-Ishikawa (IKI) (7) and implicit Kirk-Mann (IKM) (8)] iterative schemes to the same fixed point 6.000000;

ii) from Table 2, it is observed that for decreasing function, the convergence of implicit Kirk-multistep iterative scheme (2) to the fixed point 0.381966 is equivalent to the convergence of other implicit Kirk-type [implicit Kirk-Noor (IKN)(6), implicit Kirk-Ishikawa (IKI) (7) and implicit Kirk-Mann (IKM)(8)] iterative schemes to the same fixed point 0.381966.

5. Conclusion

The numerical examples considered in this paper justified our claim on the equivalence results obtained. These results show that our implicit Kirk-type hybrid iterative schemes have good potentials for further applications.