Chaos Synchronization in Discrete-Time Dynamical Systems with Application in Population Dynamics ()
Lead Paragraph
Synchronization of complex population oscillations in natural systems has been examined widely by many researchers. Due to the sensitivity on initial conditions of chaotic systems, synchronization of chaotic systems does not look to be possible. However, it has been shown that it is still possible that under some conditions, two synchronized systems in chaotic regime get synchronized again. There are many studies about how we can couple continuous time dynamical systems but we cannot find any explicit and concrete way to couple the discrete-time dynamical systems. Since discrete-time systems play important role in modeling non-overlapping generations, we have developed a novel way to couple these systems which keeps the same qualitative dynamics and we have provided one well known example of this type of coupling. Also, we have defined a new concept in the area of chaos synchronization called synchronization threshold. By passing the threshold both drive and response system lose the condition for complete synchronization and their solutions diverge from each other.
1. Introduction
Population dynamics can be modeled through the continuous-time system and the discrete-time system. However, when population size is small or that population does not overlap, discrete-time system is more appropriate to use. Discrete-time population models are widely used to describe the dynamics of hosts and parasitoids interactions [1] [2] [3]. There are many simple nonlinear discrete-time biological models which create rich and complex spectrum of dynamics from coexistence of species through periodic cycles to irregular and chaotic behaviors [4] [5] [6] [7] [8]. Chaos and synchronization are two widespread phenomena with application in many disciplines which have been considered as a central topic in nonlinear dynamics [9] [10] [11]. The presence of chaos in population models has been extensively reported by different researchers [4] [5] [6] [7] [8]. The main property of chaotic dynamics is its critical sensitivity to initial conditions, which is responsible for initially neighboring trajectories separating from each other exponentially in the course of time. Synchronization implies that there is a strong correlation between coupled systems and intuitively, it refers to a phenomenon which makes the systems have the same dynamical behavior. Traditionally, synchronization was based upon periodic signals. However, after coming to the chaotic signals, more possibilities and flexibilities have been entered in this area.
Chaos synchronization, has been started by the work of Fujisaka and Yamada [12] in 1983. After 1990, when the possibility of chaos synchronization was understood by researchers, this idea has received many attractions by people in different areas [13] [14] [15] [16] [17]. Synchronized chaos means that for any two chaotic systems for which any two nearby initial points in phase space quickly diverge and become unpredictable, it is possible that these two converge toward each other and evolve with each other in time. Complete synchronization takes place if there is a perfect linking of the chaotic solutions such that they remain in step with each other in time. In 1990, L.M. Pecora and L. Carroll, described a coupling method which constructs a real set of chaotic synchronization circuits [13]. They have applied this common signal to several well-known continuous-time dynamical systems such as Lorenz and Rossler and they claimed that it is possible to use this method with a slight variation for discrete-time dynamical systems. Chaos synchronization has great interest and application in different disciplines like physics [9] and biology [10], and it has been observed in a huge variety of phenomena in nature [11]. Synchronization has an important role in self-organization of organisms’ groups in various biological systems [18]. There are several types of synchronization, such as complete synchronization [14], generalized synchronization [19] [20] [21], phase synchronization [22], lag synchronization [23], antisynchronization and projective synchronization [24] and [25].
This study proposes a new way to couple of discrete-time dynamical systems. We study three different types of synchronization for this new coupled system and we present the results related to the local stability of drive response system and we find the attractive set of this novel coupled system. This paper also studies the interesting dynamics of a drive-response Ricker model which has been coupled by convex link function. Our goal is to build an appropriate response system which traces the drive system and finally they evolve in time even in chaotic regime. We explain that how this coupling method can be applied on a general discrete-time dynamical system to get a complete synchronization. Finally, the long term analysis through bifurcation diagrams and also time-series analysis exhibit that this drive-response system which reveals complex dynamics including cascade of period doubling to chaotic solutions, for smaller synchronization threshold, get completely synchronized.
2. Description of the Coupling Method
In this section, we study the complete synchronization in a general discrete-time drive-response system. Here, we use a convex function to build the proposed drive-response system. To begin with, consider the following discrete-time dynamical system:
 (2.1)
(2.1)
where  is the state vector of drive system at time n, f is a mapping from
is the state vector of drive system at time n, f is a mapping from  to itself and is continuously differentiable. Next step is to find a perfect linking such that the system (2.1) and new coupled one remain in step with each other in time. To model the response system or coupled system, we use a convex link function as the form
to itself and is continuously differentiable. Next step is to find a perfect linking such that the system (2.1) and new coupled one remain in step with each other in time. To model the response system or coupled system, we use a convex link function as the form  where
where  and
and  are the state vectors of response system at time n, and
are the state vectors of response system at time n, and  is synchronization threshold. Therefore, for
is synchronization threshold. Therefore, for , the response system has the form:
, the response system has the form:
 (2.2)
(2.2)
and we demonstrate the error between the solutions of the drive system (2.1) and the response system (2.2) by .
.
2.1. Complete Synchronization Using Contraction Mapping Theorem
To explain the complete synchronization between two systems (2.1) and (2.2), we need to recall some known concepts which are crucial part of the proposed coupling method:
Definition 2.1 We say that the drive system (2.1) and response system (2.2) are in complete synchronization if
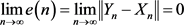 (2.3)
(2.3)
means that two systems eventually evolve identically in time.
Definition 2.2 Let E be a Banach space. Then, the map  is called a contraction mapping if there exists a constant
is called a contraction mapping if there exists a constant  such that for every pair of points
such that for every pair of points , we have
, we have , where
, where  is called a contraction constant of F on E [26].
is called a contraction constant of F on E [26].
The error between the drive and response system (2.1) and (2.2) has the following form:
 (2.4)
(2.4)
We can easily see that for :
:
![]()
Here, we assume that f is a contraction mapping. Then, for the Equation (2.4) we can write:
![]()
where, ![]() is a contraction constant.
is a contraction constant.
As we defined before, to get complete synchronization, we need to have![]() . Therefore, for contraction constant
. Therefore, for contraction constant![]() ,
,
![]()
which means that the drive-response system (2.1)-(2.2) satisfies the complete synchronization properties. We will find ![]() in theorem (2.3).
in theorem (2.3).
Theorem 2.3 Given the non-linear coupled dynamical system (2.1) and (2.2), where the map![]() , and for the values
, and for the values![]() , we get
, we get
![]()
means that passing the synchronization threshold ![]() makes the drive-response system (2.1) and (2.2) lose the complete synchronization properties.
makes the drive-response system (2.1) and (2.2) lose the complete synchronization properties.
Proof. Suppose the following ![]() maps which have a fixed point at the origin:
maps which have a fixed point at the origin:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
where the contraction mapping ![]() includes the vector-valued homogeneous polynomials of degree
includes the vector-valued homogeneous polynomials of degree![]() . Consider the following equation for the error:
. Consider the following equation for the error:
![]()
Since, we assumed that F is a contraction mapping, it satisfies the following inequality:
![]()
where, ![]() is a contraction constant. By triangular inequality we can write:
is a contraction constant. By triangular inequality we can write:
![]()
where, ![]() and
and ![]() is the spectral radius of A which is equal to
is the spectral radius of A which is equal to ![]() where
where ![]() is the root of characteristic polynomial or eigenvalue for A. Since,
is the root of characteristic polynomial or eigenvalue for A. Since, ![]() , therefore
, therefore
![]()
We know that for complete synchronization, the error between the solutions should converge toward zero. Thus,![]() . As a result, for
. As a result, for ![]() we have
we have
![]()
for which,![]() . Here,
. Here, ![]() , which we discussed in the beginning of this section. After passing
, which we discussed in the beginning of this section. After passing![]() , we lose the complete synchronization between (2.1) and (2.2).
, we lose the complete synchronization between (2.1) and (2.2).
Remark 1 Consider the drive system (2.1) becomes periodic with period![]() , i.e.,
, i.e.,![]() . Then, for the values
. Then, for the values![]() , the non-linear coupled dynamical system (2.1) and (2.2) become completely synchronized. In other word,
, the non-linear coupled dynamical system (2.1) and (2.2) become completely synchronized. In other word,
![]()
Here, similar to the proof of theorem (2.3), we decompose the nonlinear dynamical system (2.1) and (2.2) into linear and non-linear part. In this case, using triangular inequality we have:
![]()
We know that
![]()
Therefore, for ![]() we have
we have
![]()
for which,![]() .
.
2.2. Local Dynamics, Attractors and Attracting Set of Drive-Response System
We continue this section by seeking appropriate closed subset ![]() in which for drive and response system (2.1) and (2.2); where
in which for drive and response system (2.1) and (2.2); where ![]() and
and![]() , the following conditions hold:
, the following conditions hold:
1) for all![]() , then
, then![]() .
.
2) f is a contraction on![]() .
.
The Jacobian matrix for drive-response system (2.1)-(2.2) has the following form:
![]() (2.7)
(2.7)
We can immediately obtain the following result:
Proposition 2.4 Given Jacobian matrix (2.7), for which the following inequality holds:
![]() (2.8)
(2.8)
where ![]() is the contraction constant,
is the contraction constant, ![]() is the spectral radius of J and
is the spectral radius of J and ![]() for
for ![]() are the eigenvalues of Jacobian matrix J. Then, the mapping f is a contraction and the drive-response system (2.1)-(2.2) satisfies the complete synchronization properties, i.e.
are the eigenvalues of Jacobian matrix J. Then, the mapping f is a contraction and the drive-response system (2.1)-(2.2) satisfies the complete synchronization properties, i.e.
![]()
Proof. By contraction mapping theorem. Assume that the eigenvalues of the Jacobian matrix (2.7) have absolute values less than one. Then, using the contraction mapping theorem, f satisfies the contraction properties and would be a contraction mapping. Therefore, for the Equation (2.4) we can write:
![]()
where,
![]() is a contraction constant. Thus, for contraction constant
is a contraction constant. Thus, for contraction constant![]() ,
,![]() which means that the drive-response system (2.1)-(2.2) satisfies the complete synchronization properties.The schematic representation for this type of coupling to obtain complete synchronization has been demonstrated in Figure 1.Recall from the theorem (2.3) that the linearization of a given autonomous drive-response problem discrete dynamical system can be written as the form:
which means that the drive-response system (2.1)-(2.2) satisfies the complete synchronization properties.The schematic representation for this type of coupling to obtain complete synchronization has been demonstrated in Figure 1.Recall from the theorem (2.3) that the linearization of a given autonomous drive-response problem discrete dynamical system can be written as the form:
![]() (2.9)
(2.9)
![]()
Figure 1. The schematic diagram for complete synchronization in a discrete-time drive-response dynamical system.
where, ![]() and
and ![]() is a sufficiently smooth governing transition function.
is a sufficiently smooth governing transition function.
Remark 2. For drive-response system (2.9), the following hold:
1) For all![]() , then
, then![]() .
.
2) h is a contraction on![]() .
.
Therefore, we have the following statements for system (2.9).
Proposition 2.5 Consider the drive-response system ![]() which is defined on a closed subset
which is defined on a closed subset ![]() and satisfies the conditions in remark (2.2). Then, there exists a unique
and satisfies the conditions in remark (2.2). Then, there exists a unique ![]() with
with![]() . In another word, if (2.8) holds, then the drive-response system (2.9) has a unique fixed point.
. In another word, if (2.8) holds, then the drive-response system (2.9) has a unique fixed point.
Remark 3 According to the well known contraction mapping theorem, the converse of proposition (2.5) does not necessarily hold.
For drive-response system (2.9), we can establish notions of sequential convergence and hence of stability for drive-response system (2.9). We now provide a general theorem which is the result of proposition (2.4).
Theorem 2.6 Let ![]() be a continuously differentiable map defined on a closed subset
be a continuously differentiable map defined on a closed subset ![]() and let J satisfying the form (2.7) be the Jacobian matrix of drive-response system (2.9) with
and let J satisfying the form (2.7) be the Jacobian matrix of drive-response system (2.9) with ![]() and
and ![]() . Then, the following hold:
. Then, the following hold:
1) The solutions ![]() of drive-response system (9) completely synchronized.
of drive-response system (9) completely synchronized.
2) Equilibrium ![]() of drive-response system (9) is stable; i.e.
of drive-response system (9) is stable; i.e.
for any![]() , there exists
, there exists ![]() such that
such that ![]() implies that
implies that ![]() for
for![]() .
.
Proof. The proof is straightforward.
Remark 4 In theorem (2.6), hyperbolicity is a robust property and it is one of the most important assumptions.
It has been experimentally observed that there may be some situations in which the response system is stable but the response system has complex dynamics and the reason is using non differentiable link function or any non-differentiable transport system. In this study, we take the advantages of using a continuous convex link function which can completely control over the behavior of response system and we will numerically show that the response system inherits the same qualitative dynamics as its drive system and even for smaller synchronization threshold, the response system and drive system are almost completely equivalent.
3. Application of Chaos Synchronization in Population Dynamics
The chaotic behavior may be observed experimentally in natural systems in many scientific areas. Chaos can be defined as irregular and unpredictable time evolution of non linear systems. Main characteristic of chaos is sensitivity on initial conditions and that system does not repeat its past behavior. Despite the fact that chaotic systems are sensitive to initial conditions, it has been experimentally shown that the chaotic oscillators could be coupled. Chaos synchronization occurs when a chaotic oscillator drives another chaotic oscillator and is a very important phenomenon which has been occurred widely in ecological systems [27] [28] [29] [30]. Because of importance of synchronization and its consequences on population dynamics, we study Ricker model and its synchronized system and we present their qualitative dynamics using different dynamical system tools.
The Ricker model is one of the most widely-used ecological models which displays regular and irregular complex nonlinear dynamics [31] [32] and its coupled system as the following form:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
where
![]() (3.3)
(3.3)
Here, ![]() demonstrates the population size of drive system,
demonstrates the population size of drive system, ![]() represents the population size of response system, r is the intrinsic growth rate, k is the carrying capacity of the environment,
represents the population size of response system, r is the intrinsic growth rate, k is the carrying capacity of the environment, ![]() is synchronization threshold and
is synchronization threshold and ![]() is a link function which has been used to couple (3.2) and (3.2). Thus, if drive system
is a link function which has been used to couple (3.2) and (3.2). Thus, if drive system![]() , the corresponding response system would be
, the corresponding response system would be![]() , where H is a function of
, where H is a function of ![]() and
and![]() .
.
For drive-response (3.2)-(3.2), the steady states are![]() ,
, ![]() , and
, and![]() . The Jacobian matrix for (3.1)-(3.2) has the form
. The Jacobian matrix for (3.1)-(3.2) has the form
![]() (3.4)
(3.4)
where
![]()
![]()
![]()
Then, at the origin we have
![]()
and for the positive fixed point ![]() we have
we have
![]()
Also, for![]() ,
,
![]()
Proposition 3.1 The local stability analysis results for the fixed points of (3.1)-(3.2) are summarized as below:
1) The equilibrium point ![]() for
for ![]() is a saddle point, and for
is a saddle point, and for ![]() is an unstable fixed point.
is an unstable fixed point.
2) The equilibrium point ![]() is a stable point in the interior of positive quadratic if
is a stable point in the interior of positive quadratic if ![]() and
and![]() , or
, or ![]() and
and![]() .
. ![]() is a saddle point if
is a saddle point if ![]() or
or![]() .
.
3) The equilibrium point ![]() for
for ![]() or
or ![]() is an unstable point, and for
is an unstable point, and for ![]() is a saddle point.
is a saddle point.
To study the global stability of the equilibrium points of both systems, at first we prove that all solutions in the first quadrant ![]() are eventually bounded.
are eventually bounded.
Theorem 3.2 For ![]() and initial conditions in the first quadrant
and initial conditions in the first quadrant![]() , i.e.
, i.e. ![]() and
and![]() , for system of (3.1)-(3.2) we have:
, for system of (3.1)-(3.2) we have: ![]() and
and ![]() for all
for all![]() . In addition, we can find some positive number M, such that
. In addition, we can find some positive number M, such that![]() .
.
Proof. By induction.
Since ![]() we have
we have![]() , hence
, hence
![]()
Assume that for![]() , we have
, we have![]() . Then for
. Then for ![]() we have
we have
![]()
Therefore ![]() for any
for any![]() . Similarly, since
. Similarly, since ![]() and
and ![]() , we have
, we have ![]() is positive. Hence,
is positive. Hence,
![]()
Assume that for![]() , we have
, we have![]() . Then for
. Then for ![]() we have
we have
![]()
Therefore ![]() for any
for any![]() . To find an upper bound, we know,
. To find an upper bound, we know,
![]()
If we define![]() , then
, then ![]() and
and ![]() has critical points at
has critical points at![]() . Since
. Since ![]() if
if ![]() and
and ![]() if
if![]() , then
, then ![]() is the maximal point of
is the maximal point of![]() , i.e.
, i.e.![]() . Hence,
. Hence,
![]()
Similarly,
![]()
Therefore, we can find some positive number M, such that ![]() .
.
Theorem 3.3 If there are positive constants ![]() and
and ![]() such that the solution
such that the solution ![]() of system satisfies
of system satisfies
![]()
![]()
Then, system (3.1)-(3.2) is persistent. If system is not persistent, it is called non-persistent [33].
Theorem 3.4 Given ![]() and initial conditions
and initial conditions ![]() and
and ![]() in system (3.1)-(3.2), if the following conditions hold:
in system (3.1)-(3.2), if the following conditions hold:
1) ![]()
2) ![]()
Then for drive-response system (3.1)-(3.2) for ![]() we have,
we have,
![]()
where
![]() (3.5)
(3.5)
Proof. Using theorem (2.6), since ![]() is closed and the conditions of proposition (2.4) are satisfied, therefore the solutions of drive-response system (3.1)-(3.2) are completely synchronized and the error between the solutions converges toward zero.
is closed and the conditions of proposition (2.4) are satisfied, therefore the solutions of drive-response system (3.1)-(3.2) are completely synchronized and the error between the solutions converges toward zero.
3.1. Phase and Amplitude Synchronization in Population Dynamics
We begin with two important concepts in theory of synchronization of chaotic systems: a) mean phase difference, b) mean amplitude difference. We analyze these two types of synchronizations for drive-response population model (3.1)-(3.2) which have been coupled using the proposed link function. We consider the oscillations of this discrete-time population system as being synchronized if their phases coincide repeatedly and they have identical mean amplitude. These two types of synchronization have been studied widely in science, nature, engineering, or social life [34] - [39] and before using them, we briefly define them.
Definition 3.5 We call two systems are in phase synchronization if they have equivalent mean phase or they have a constant difference in phase. We define mean phase for two oscillators as
![]() (3.7)
(3.7)
where, ![]() is the number of cycles within a time
is the number of cycles within a time![]() .
.
In fact, for two non-identical oscillators, phase synchronization happens when their phases evolve in synchrony but their amplitude remain unsynchronized.
Definition 3.6 We call two systems are in amplitude synchronization if they have identical mean amplitude. We define mean amplitude for two oscillators as
![]() (3.8)
(3.8)
Remark 5 The mean amplitude and mean phase are qualitatively similar with each other.
Figure 2 demonstrates the mean phase difference, i.e. ![]() and the mean amplitude difference, i.e.
and the mean amplitude difference, i.e. ![]() corresponding to Ricker model and its synchronized model (3.1) and (3.2). As we can see, using these two tools, we can numerically catch the threshold at which the systems (3.1) and (3.2) satisfy the phase synchronization and amplitude synchronization properties.
corresponding to Ricker model and its synchronized model (3.1) and (3.2). As we can see, using these two tools, we can numerically catch the threshold at which the systems (3.1) and (3.2) satisfy the phase synchronization and amplitude synchronization properties.
3.2. Complete Synchronization in Population Dynamics
In this section, we study the complete synchronization for drive-response system (3.1)-(3.2) using some qualitative methods which have been used frequently to detect chaos. In order to understand some dynamical behaviors of systems including period doubling bifurcations and chaotic oscillations, we picked a single parameter bifurcation, which can demonstrate how dependence is the dynamics of the systems on a certain parameter.
Figure 3 demonstrates the solutions of drive system (3.1) (red color) and response system (3.2) (black color) with different initial conditions and some interesting r values while![]() .
.
For ![]() and
and ![]() both drive and response system (3.1)-(3.2) evidently, exhibit the sigmoidal approach to carrying capacity reminiscent of the logistic model. For
both drive and response system (3.1)-(3.2) evidently, exhibit the sigmoidal approach to carrying capacity reminiscent of the logistic model. For![]() , we have damped oscillations toward steady state which is because of two biological phenomena at first, the population which started below carrying capacity does not smoothly approach steady state through a phenomenon called as overcompensation and then this follows by the second phenomenon called undershooting, which is due to further overshooting. If we increase r further, for the value
, we have damped oscillations toward steady state which is because of two biological phenomena at first, the population which started below carrying capacity does not smoothly approach steady state through a phenomenon called as overcompensation and then this follows by the second phenomenon called undershooting, which is due to further overshooting. If we increase r further, for the value ![]() we see that these damped oscillations follows by a 2-cycle pattern and they are diverging from the steady states. Similarly, for
we see that these damped oscillations follows by a 2-cycle pattern and they are diverging from the steady states. Similarly, for ![]() and
and![]() , the oscillations follow a 2-cycle pattern. Finally, for
, the oscillations follow a 2-cycle pattern. Finally, for ![]() we can see the occurrence of unpredictable, irregular and chaotic oscillations.
we can see the occurrence of unpredictable, irregular and chaotic oscillations.
![]()
Figure 2. The mean phase difference and the mean amplitude difference for drive-response system (3.1)-(3.2) when![]() .
.
In Figure 4 and for the case![]() , we have almost the same dynamics as we had for
, we have almost the same dynamics as we had for![]() . As we can see, for larger values of threshold s, we do not get completely synchronized cycles.
. As we can see, for larger values of threshold s, we do not get completely synchronized cycles.
Indeed, displayed dynamics in Figure 3 and Figure 4 are not special to the Ricker model, but are common features of discrete time population models.
For Figure 5, we explain some general properties which have been shared between the drive-response system (3.1)-(3.2) in common. As we can see, with increasing r the value of carrying capacity k is increasing. However, for ![]() the branch corresponding to stable steady states bifurcates through period-doubling bifurcation into a 2-cycle. As we increase r further, the interval over which we have a new period reduces, and as we know this smaller and smaller windows are called Feigenbaum cascade which after them the dynamics become aperiodic. As we expected, the bifurcation diagram of drive-response system (3.1)-(3.2) for greater values of s, shows the same types of dynamics for drive and response system, but not completely synchronized.
the branch corresponding to stable steady states bifurcates through period-doubling bifurcation into a 2-cycle. As we increase r further, the interval over which we have a new period reduces, and as we know this smaller and smaller windows are called Feigenbaum cascade which after them the dynamics become aperiodic. As we expected, the bifurcation diagram of drive-response system (3.1)-(3.2) for greater values of s, shows the same types of dynamics for drive and response system, but not completely synchronized.
The Poincare section and power spectrum of drive-response system (3.1)-(3.2) have been displayed in Figure 6 for the case![]() ,
, ![]() and
and![]() . Basically, the Poincare section can be constructed by sampling the phase portrait which helps to simplify the complicated dynamical systems. It is known that periodic behavior corresponds to a fixed point in Poincare section and any chaotic dynamics can be detected by set of distinct points in Poincare map. Moreover, the wideband chaotic signals and periodic signals can be easily distinguished from each other using the frequency spectra. Therefore, as we understood from bifurcation diagram, drive-response system (3.1)-(3.2) experiences the chaotic dynamics for
. Basically, the Poincare section can be constructed by sampling the phase portrait which helps to simplify the complicated dynamical systems. It is known that periodic behavior corresponds to a fixed point in Poincare section and any chaotic dynamics can be detected by set of distinct points in Poincare map. Moreover, the wideband chaotic signals and periodic signals can be easily distinguished from each other using the frequency spectra. Therefore, as we understood from bifurcation diagram, drive-response system (3.1)-(3.2) experiences the chaotic dynamics for ![]() and as we expected for large values of s we can not establish a complete synchronization.
and as we expected for large values of s we can not establish a complete synchronization.
4. Conclusion
Synchronization in population dynamics can lead to arising complex dynamics and understanding the synchronization of oscillations is crucially important in
![]()
Figure 5. Bifurcation diagram of Ricker model and its coupled with the error between their attractors for ![]() and
and![]() , drive system (red color) and response system (black color).
, drive system (red color) and response system (black color).
this area. In this study, we developed a new drive-response system by defining a convex continuous link function which maps the orbits of the drive system keeping the same qualitative properties such as stability and periodicity into the orbits of its coupled system. As has been shown by L. M. Pecora and T. L. Carroll, in 1990, two Lorenz systems with the property of sensitive dependence on the initial conditions could be synchronized starting from different initial states. We extended this result into discrete-time dynamical systems and we have shown that by using the concept of convex function, we can force the orbits of a discrete-time drive-response system starting from different initial conditions to get synchronized and we observed that this coupling method can be successful for drive-response system (3.1)-(.3.2) to get a complete synchronization when the synchronization threshold has smaller values, closer to zero. We also changed the values of synchronization threshold s in its range between (0,1) and we observed that the response system (3.2) for larger values of synchronization threshold s is not completely synchronized with its original drive system (3.1) and when we increased the values of synchronization threshold s, we also noticed that the qualitative behaviors of both systems remain the same, even though, we do not get a complete synchronization between the solutions of drive and response system (3.1)-(3.2). In chaotic regime, for larger values of synchronization threshold s, closer to one, we could not get a complete synchronization. But, for smaller synchronization threshold s, closer to zero, we have shown that two systems are in complete synchronization even though the dynamics is chaotic.
Acknowledgements
This work was supported by the Institute of Computational Comparative Medicine (ICCM) and department of Mathematics of Kansas State University. With a special thanks to Dr. Majid Jaberi-Douraki for his full support.