昨年末の課題に設定した「離心率のグラフ表示」にとりあえず成功しました。
ソースはこちら。
細かな内容検討はこれからです。
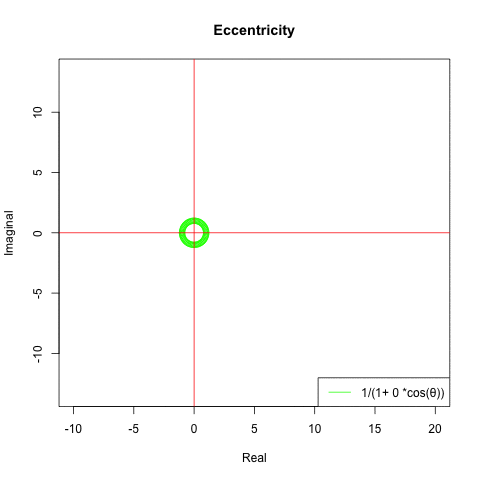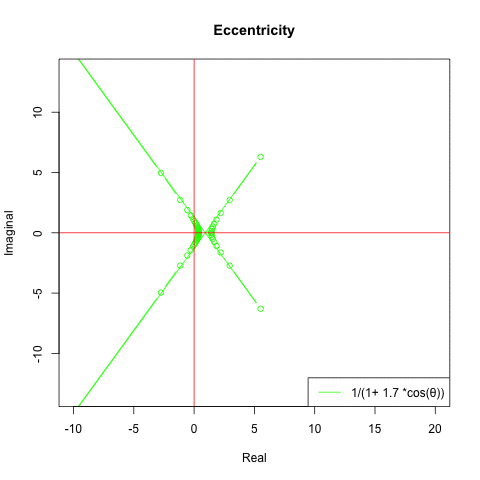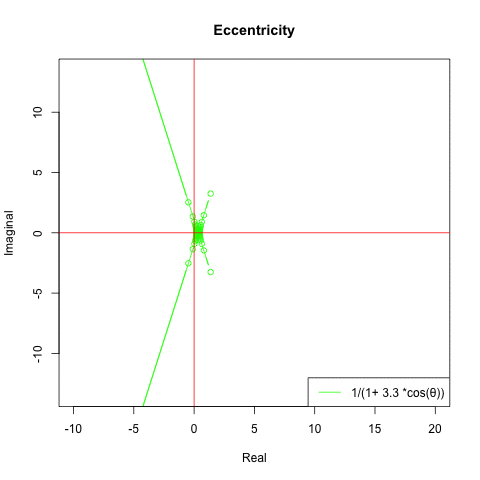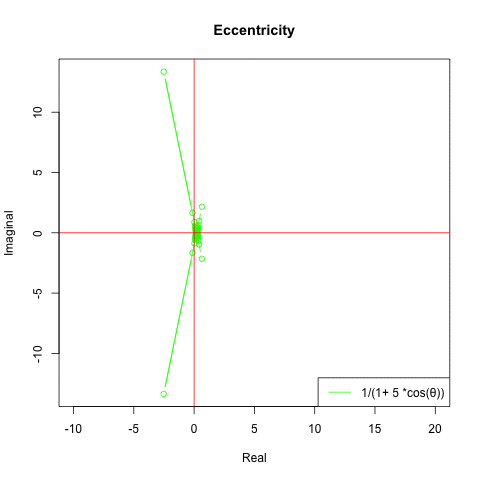
とりあえず離心率関数1/(1+離心率ε×cos(θ))を動かしてみました。極座標系(Polar Coordinates System)なので絶対値(Module)=上掲式、角度(Argment)θ=-π→πの複素数表現(Complex Expression)を合成してPlotしています。

- 離心率ε=0の時に半径1の単位円
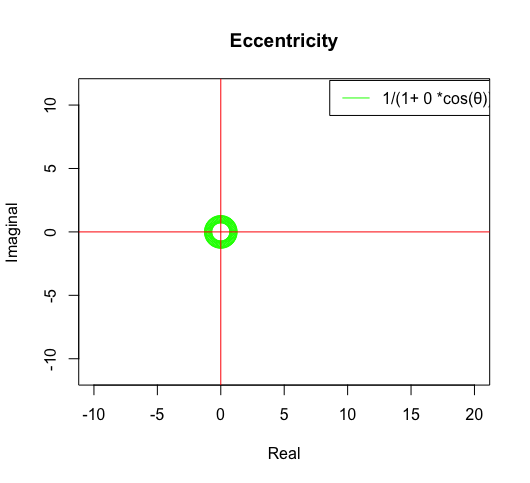
- 離心率0<ε<1の時に楕円
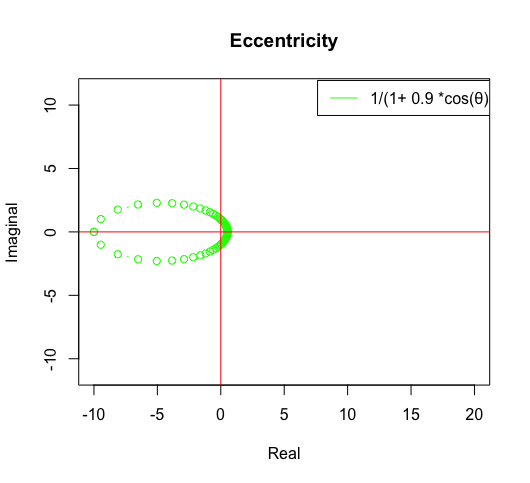
- 離心率ε=1の時に放物線
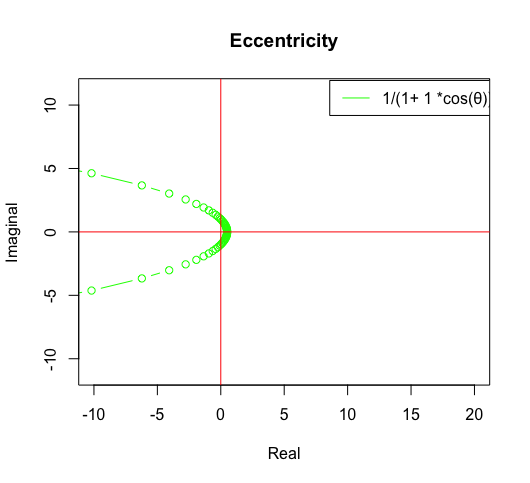
- 離心率ε>1の時に双曲線
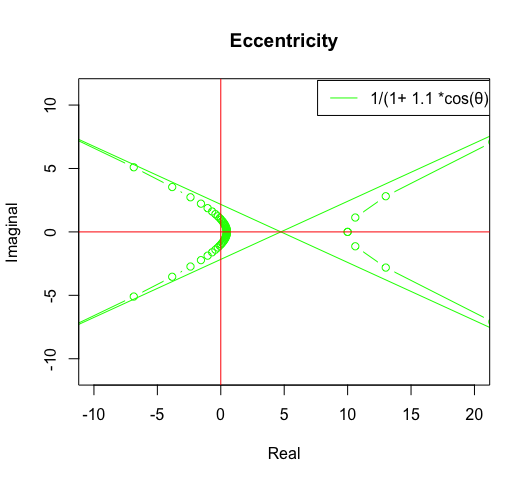
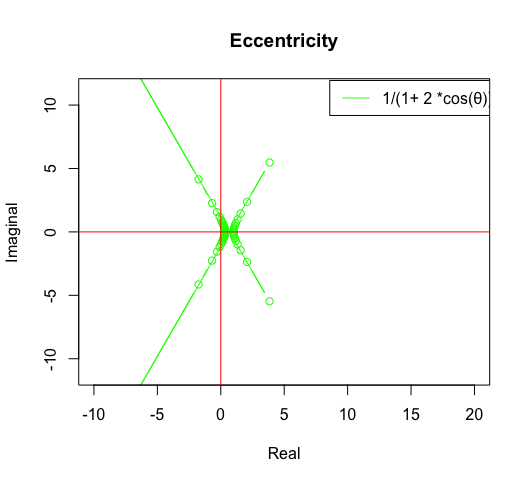
そして離心率εが無限大Inf(inity)に近くにつれY軸上の原点{0,0}へと収束していきます。
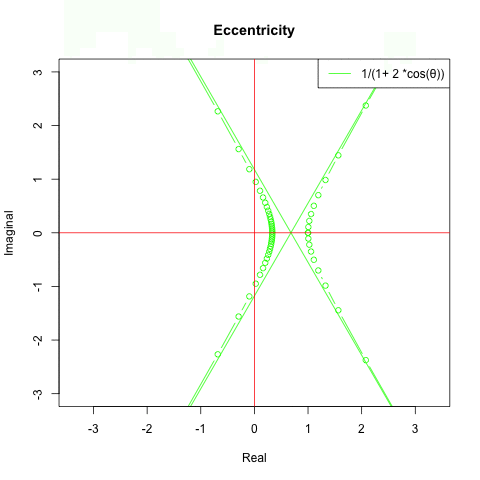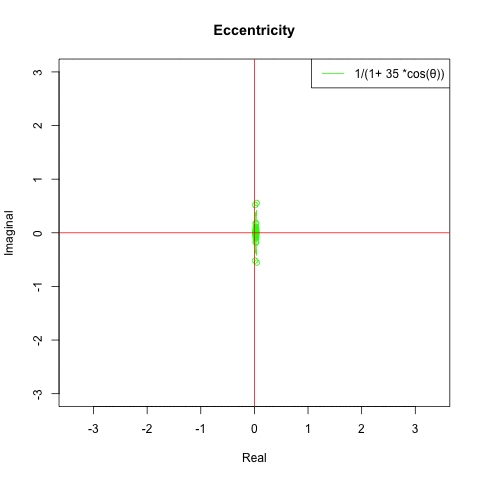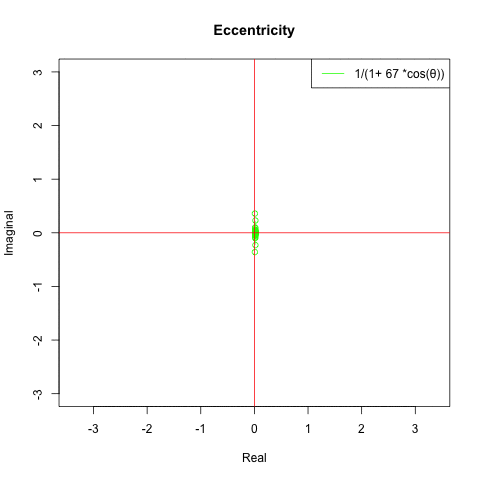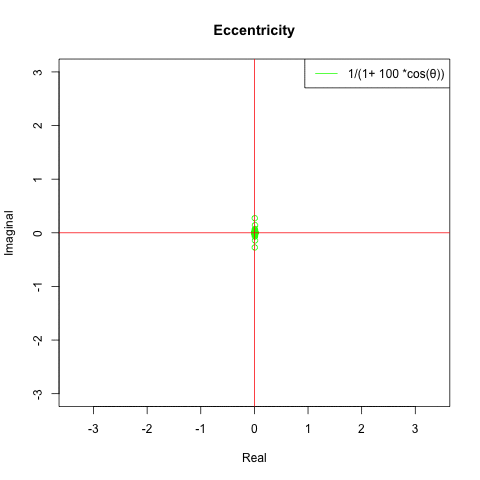
特に双曲線の動きが謎…そんな感じで以下続報…