数学はもっと基本中の基本をまとめて伝える努力をした方がいいかもしれません。例えば実際、小学校で習う等比数列と等差数列の概念がどうやって群論における加法群と乗法群に接続するのか当たりが着くまで数年を要してしまいました。

均等尺座標系(Equal scale coordinate system)…群論の基本では自然数集合(Natulal Set)、すなわち初項(First Term)α=1,公差(Common Difference)d=1,一般項(General Term)α+(n-1)dの等差数列(Arithmetic Sequence=算術数列)Nn(n=1→Inf(inity)){1+(1-1)×1=1,1+(2-1)×1=2,1+(3-1)×1=3,…,1+(Inf(inity)-1)×1=Inf(inity)}={1,2,3,…,Inf(inity)}の逆元に加法単位元(Additive Identity)0と逆元-N(Inverse Element)を加えたものを加法整数群(Additive Integer Group)Zn(n=-Inf→-1→0→1→Inf){-Inf,…,-3,-2,-1,0,1,2,3,…,Inf}と呼ぶ。10進法の位取り概念を導入して小数点下の数字も扱える形に拡張しても、あくまで振られている目盛りが均等尺である事実は動かない。



対数尺座標系(Logarithmic Scale Coordinate System)…上掲の均等尺座標系を以下の形に射影したのが対数尺座標となる。
この時、均等尺座標系上の1はexp(1)(1+1=2→2.718282)に、-1はexp(-1)(1-1=0→0.3678794)に射影される。どの冪乗算(Exponentiation)も(すなわち任意の公比の等比数列は)底の変換公式log(a base=b)=log(a)/log(b)によってこの「公比ネイピア数の等比数列」へと変換可能である。すなわちこの考え方では(上掲の形で10進法導入に拠って小数点下も扱える様になった加法整数群を元とする)加法群に対応する(すなわち添字集合を共有する)乗法群がただ一つだけ存在している事になる。
- この座標系の最大の特徴は均等尺座標系上における乗算が加算に、除算が減算に(そして冪算が乗算に)置き換えられる事で、人類が最初にこの座標系に注目したのもその特徴からだった(コンピューター発明を促した常用対数表の利用)。
- 任意の(すべての)正の実数は全てα×2^n(1≦α<2;nは整数)の形によって、そして任意の対数はこの式の対数版たるlog(α)+n×log(2)によって表せる。数列的にはどちらもこ「1から2にかけて連続する実数集合」を周期単位(Unit Cycle)、「2あるいはllog(2)の個数」を添字単位(Unit Index)とする剰余群を興成する。
こうした両者の関係とこれまで述べてきた様なある種の「座標進化論」とはどう結びついてくるのでしょうか?
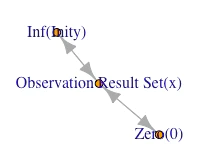
①まずは(それ自体は観測対象となり得ない)観測原点(Observation Origin)0と観測限界(およびその向こう側に横たわるObservation Limit)Inf(inity)の間に「何もない」状態から出発する。いわば観測自体成立していない、すなわち「閉じた目蓋の向こう側に全てがある」様な状態。
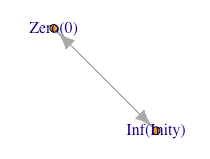
- exp(-1)(0.3678794)を求めるベルヌーイの式(1-1/n)^nにおけるn=1(すなわち(1-1/1)^1=0)の場合に該当する。未開封のくじ引きセットの様なもので当たりなら必ず入っており「外れる確率」を計算しても0にしかならないのである。
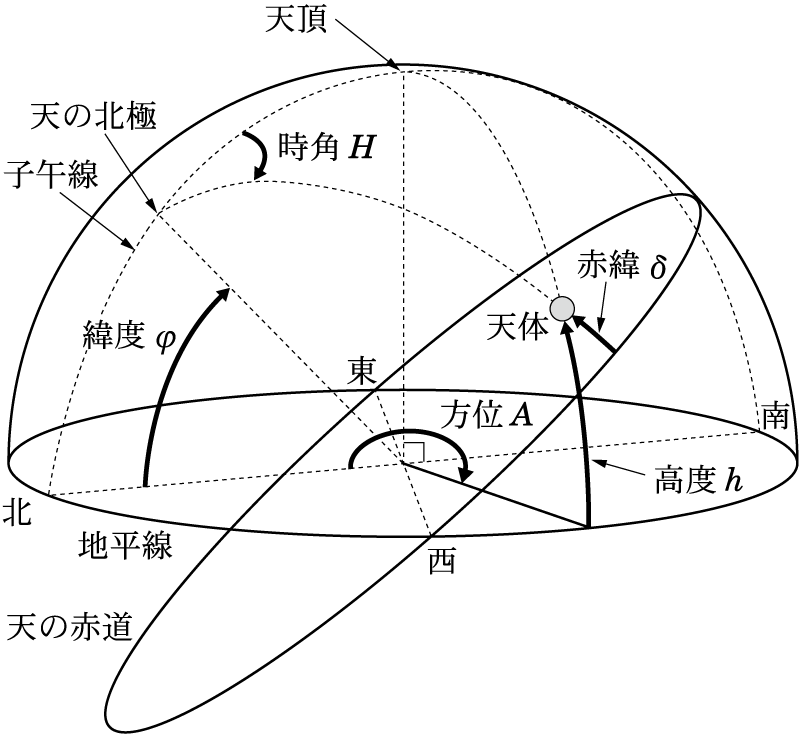
②観測原点(Observation Origin)0と観測限界(およびその向こう側に横たわるObservation Limit)Inf(inity)の狭間に何か得られる様になっても、各観測結果の関係が互いに素では次元抽出も相対距離も測れない。この段階における観測空間はある意味観測原点を中心に円弧状、もしくは球面状に均等に広がっているといえよう。


③次元抽出や中心割り出しが可能そうな有望な観測結果集合が得られて初めて「統計科学的/確率論アプローチ」が可能となる。この段階では確実に頼れる(逆を言えば無視を許されない)実軸(Real Axis)は1本もなく、作業用に引かれた補助線は全て虚軸(Imaginal Axis)に分類される。




- あくまで座標論的に「まだ空間そのものに一切目盛りが振れない」段階に過ぎず、本当に「信頼可能なデータの取得が不可能な状態」とも限らない点に注意。実際MCMC法の広まりや機械学習の台頭はこういう問題とリンクしてくる。

④(最大値と最小値の中間としての平均が求まるなどして)観測円が成立してやっと「片側無限数列(One Side Inf(inity) Sequance)=半径(Radius)のみの世界」から「両側無限数列(Both Side Inf(inity) Sequance)=直径(Diameter)もある世界」に推移するが「最初の実軸=スカラー」であり、まだ大小の区別くらいしか伴わない上に偶奇性の様な新概念も追加となる。



最近、上掲の③と④の狭間に大きな見落としがある事に気付いてしまったのです。
- 「観測原点の観測円への拡張」がそのまま「数直線の登場」に直結すると考えていたのが間違っていた。実はその結果現れるのは大半径(Major Radius)1,小半径(Minor Radius)1のトーラス構造と考えるのが自然なのではなかろうか。

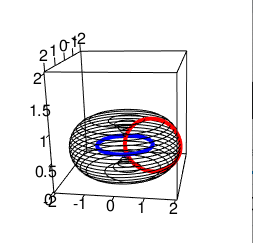
- そして複素関数論の世界ではかかる多値状態を克服するのに「切断(Branch Cut)」なる技法を用いる。上掲の様な(実軸の周囲を虚軸が巡る)円筒状態への拡張もこの段階を経ると考えられる。


- そして「ドーナツの様に湾曲したトーラス」をアイロンを当てた様に真っ直ぐ伸ばして連ねて「(上掲の)正負方向に無限に続く円筒状態」を実現するには、半円描画関数-1^x(x=0→1)=(0±1i)^2xに2/πを掛けた上、上掲の「均等尺座標系から対数尺系への変換」が必要(とも考えられる。まだ理屈で把握は出来てない。現段階ではただの直感に過ぎない)。
「ただの直感」とはいえ。この処理には思い当たる節があるのです。そう、式の構成要素がオイラーの等式(Eulerian Identity)e^πi=(1±πi/n)^n=-1そのものじゃありませんか。ただしプロセスは真逆で、こちらは「長さπの直線が円弧を河童巻きにする」様に見えるのです。なるほど…

- ここでいう(±)πとはトーラス構造の小円上における原点0からその対蹠(±)2までの円弧上の距離だった。そしてピッチを揃える(縦軸と横軸の目盛りを揃える為に)為、均等尺座標系から対数尺座標系への変換に際してはπ/2、逆に対数尺座標系から均等尺座標系への変換に際しては2/πを掛ける。ここに登場する2は小学生の時習う等比数列-1^x(-1と1の間を往復する交代級数)を「円を描く」複素関数(0±1i)^2xに拡張出来て初めて見えてくるのだが、ガウスやオイラーの時代にはまだまだ複素数概念を否定する守旧派学者が多く、その事を直接公言するのが憚られ、例え口にしたとしても広まらなかったのであろう。
おそらく、そうしたリスクをも孕む交代級数概念を駆使したテイラー級数やマクローリン級数が(イングランドとの合併に伴う既存社会の崩壊によって伝統的価値観の拘束が一時的に緩み、功利主義の様な大胆な考え方を次々と輩出したものの、フランス革命勃発を受けて守旧派が盛り返し思想統制の徹底によって壊滅した)啓蒙主義時代スコットランドにおいて育まれたのは、決して偶然ではなかった。そもそもアイザック・ニュートン(Sir Isaac Newton、1642年~1727年)が画期的な万有引力のアイディアを得たのはロンドンにおけるペスト大流行を受けてケンブリッジ大学が閉鎖され教職を解かれていた1665年~1666年頃、ライプニッツ(Gottfried Wilhelm Leibniz, 1646年~1716年)による微積分法の発見(1675年)もまたそれまで庇護者だったマインツ選帝侯に先立たれ失職した1673年から新たにハノーファー宮廷に仕える様になった1676年の間のパリ滞在期だったりする。そして「ベイズの定理(Bayesian Theorem)」で知られるトーマス・ベイズ(Thomas Bayes, 1702年~1761年)に至っては、イングランド出身ながら国教徒ではなかった為にオックスフォード大学やケンブリッジ大学に入れなかった異端児だった。オイラーも立身出世に無頓着なタイプでドイツ宮廷では疎まれ、最終的に僻地のロシア宮廷の落ち着いている。こうして全体像を俯瞰すると近世から近代におけるある種のアカデミズム界中央が、新たな着想を育むのに適した場所ではなかった状況が透けて見えてくるのである。
- 特に重要なのが上掲の「分枝切断による(符号の区別のない)片側無限数列から(符号の区別がある)両側無限数列への拡張」とオイラーの等式のうち-1に無限にたどり着けない式形(1-πi/n)^nの関係である。何故ならそれは「(x^-1=1/xの式形に対応するLog(2)を計算不能とする)特異点(Singularity)」概念とも絡んでくるトピックだから。

「(グルグル無限に回り続ける)多価状態」を両側無限数列に変形させるとはこういう事だったのですね。それが明らかになった時点で以下続報。近代数学と現代数学の狭間に横たわる海溝がここまで深いとは…