Theoretical Quantization of Exact Wave Turbulence in Exponential Oscillons and Pulsons ()
1. Introduction
The experimental Deterministic Scalar Kinematic (eDSK) structures, the theoretical Deterministic Scalar Kinematic (tDSK) structures, the experimental Deterministic Vector Kinematic (eDVK) structures, the theoretical Deterministic Vector Kinematic (tDVK) structures, the experimental Deterministic-Deterministic Scalar Dynamic (eDDSD) structures, the theoretical Deterministic-Deterministic Scalar Dynamic (tDDSD) structures, the experimental Deterministic-Deterministic Vector Dynamic (eDDVD) structures of the mth and nth families, and the theoretical Deterministic-Deterministic Vector Dynamic (tDDVD) structures of the mth and nth families have been constructed in [1] to obtain the exact solution for deterministic chaos and to describe quantization of the kinetic energy of deterministic chaos in terms of deterministic exponential oscillons and pulsons for the Fourier set [2] and the Bernoulli set [3] of wave parameters.
The experimental Random Scalar Kinematic (eRSK) structures, the theoretical Random Scalar Kinematic (tRSK) structures, the experimental Random Vector Kinematic (eRVK) structures, the theoretical Random Vector Kinematic (tRVK) structures, the experimental Random-Random Scalar Dynamic (eRRSD) structures, the theoretical Random-Random Scalar Dynamic (tRRSD) structures, the experimental Random-Random Vector Dynamic (eRRVD) structures of the mth and nth families, and the theoretical Random-Random Vector Dynamic (tRRVD) structures of the mth and nth families have been generated in [2] to find the exact solution for stochastic chaos and to represent theoretical quantization of the kinetic energy of stochastic chaos in random exponential oscillons and pulsons.
To compute the exact solution for wave turbulence governed by the nonstationary Navier-Stokes equations in three dimensions with the help of the method of Decomposition in Invariant Structures (DIS), the mentioned invariant structures have been complemented by the experimental Deterministic-Random Scalar Dynamic (eDRSD) structures, the theoretical Deterministic-Random Scalar Dynamic (tDRSD) structures, the experimental Random-Deterministic Scalar Dynamic (eRDSD) structures, the theoretical Random-Deterministic Scalar Dynamic (tRDSD) structures, the experimental Deterministic-Random Vector Dynamic (eDRVD) structures of the mth and nth families, the theoretical Deterministic-Random Vector Dynamic (tDRVD) structures of the mth and nth families, the experimental Random-Deterministic Vector Dynamic (eRDVD) structures of the mth and nth families, and the theoretical Random-Deterministic Vector Dynamic (tRDVD) structures of the mth and nth families.
Following [2] [3] [4] , the rectangular, diagonal, and triangular summations of matrices of the turbulent kinetic energy and general terms of numerous sums have been employed in this paper to work out theoretical quantization of the turbulent kinetic energy of exact wave turbulence. Nested structures of a cumulative energy pulson, a deterministic energy pulson, a deterministic internal energy oscillon, a deterministic-random internal energy oscillon, a random internal energy oscillon, a random energy pulson, a deterministic diagonal energy oscillon, a deterministic external energy oscillon, a deterministic-random external energy oscillon, a random external energy oscillon, and a random diagonal energy oscillon have been defined.
The energy pulsons and oscillons enclose deterministic group pulsons, deterministic internal group oscillons, deterministic-random internal group oscillons, random internal group oscillons, random group pulsons, deterministic diagonal group oscillons, deterministic external group oscillons, deterministic-random external group oscillons, random external group oscillons, and random diagonal group oscillons, respectively.
The group pulsons and oscillons incorporate deterministic wave pulsons, deterministic internal wave oscillons, deterministic-random internal wave oscillons, random internal wave oscillons, random wave pulsons, deterministic diagonal wave oscillons, deterministic external wave oscillons, deterministic-random external wave oscillons, random external wave oscillons, random diagonal wave oscillons, correspondingly.
The wave pulsons and oscillons are constructed of deterministic elementary pulsons, deterministic internal elementary oscillons, deterministic-random internal elementary oscillons, random internal elementary oscillons, random elementary pulsons, deterministic diagonal elementary oscillons, deterministic external elementary oscillons, deterministic-random external elementary oscillons, random-deterministic external elementary oscillons, random external elementary oscillons, and random diagonal elementary oscillons, congruently.
The contents of this paper are as follows. In Section 2, decompositions of summation matrices of various constituents of the turbulent kinetic energy are constructed. The deterministic, wave, group, and energy pulsons are defined in Section 3. Section 4 deals with the deterministic, diagonal, wave, group, and energy oscillons. The deterministic, internal, wave, group, and energy oscillons are described in Section 5, which is proceeded by Section 6 dealing with the deterministic, external, wave, group, and energy oscillons.
In Section 7, we treat the deterministic-random, internal, wave, group, and energy oscillons. Section 8 is devoted to the deterministic-random, external, wave, group, and energy oscillons. The random, wave, group, and energy pulsons are considered in Section 9. Section 10 discusses the random, diagonal, wave, group, and energy oscillons. The random, internal, wave, group, and energy oscillons are introduced in Section 11. Section 12 describes the random, external, wave, group, and energy oscillons.
The deterministic elementary oscillons and pulsons, the random elementary oscillons and pulsons, the deterministic-random and random-deterministic elementary oscillons are specified in Section 13, Section 14, Section 15, respectively. Section 16 contains a summary of theoretical quantization of the kinetic energy of exact wave turbulence that includes 42 theoretical exponential pulsons and oscillons. A concise list of open problems is also described there.
2. Decompositions of Summation Matrices of the Turbulent Kinetic Energy
The kinetic energy  of exact wave turbulence of exponential oscillons and pulsons in a Newtonian fluid with a constant density
of exact wave turbulence of exponential oscillons and pulsons in a Newtonian fluid with a constant density  and a turbulent velocity field
and a turbulent velocity field , which is a superposition of a velocity field
, which is a superposition of a velocity field  of a deterministic flow and a velocity field
of a deterministic flow and a velocity field  of a random flow, is defined by (306) of [5] as
of a random flow, is defined by (306) of [5] as
 (1)
(1)
where  is formed by velocity fields
is formed by velocity fields  and
and  of I deterministic wave groups, i.e.
of I deterministic wave groups, i.e.
 (2)
(2)
 is generated by velocity fields
is generated by velocity fields 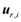 and
and  of I random wave groups, viz.
of I random wave groups, viz.
 (3)
(3)
where  and
and  are indices of deterministic and random wave groups,
are indices of deterministic and random wave groups, .
.
Substituting (2)-(3) in (1) and combining sums yields
 (4)
(4)
For clarification of nested summation matrices, primarily, we define a rectangular summation matrix of the deterministic kinetic energy
![]() (5)
(5)
a rectangular summation matrix of the deterministic-random kinetic energy
![]() (6)
(6)
a rectangular summation matrix of the random-deterministic kinetic energy
![]() (7)
(7)
and a rectangular summation matrix of the random kinetic energy
![]() (8)
(8)
where ![]() and
and![]() .
.
Kinetic energy (4) may be written via summation matrices (5)-(8) as follows:
![]() (9)
(9)
where a braces notation ![]() denotes the rectangular summation of all elements of a summation matrix
denotes the rectangular summation of all elements of a summation matrix ![]() in
in ![]() and
and![]() , e.g.
, e.g.
![]() (10)
(10)
So, elements of rectangular summation matrices (5)-(8) are dot products of velocity fields of all deterministic and random wave groups.
Since the velocity fields of I deterministic wave groups are expanded in the tDVK structures (227) of [5]
![]() (11)
(11)
and the velocity fields of I random wave groups are expanded in the tRVK structures (113) of [4]
![]() (12)
(12)
summation matrices (5)-(8) may be written in the following form:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
where the summation braces ![]() signify the rectangular summation of all matrix elements of a summation matrix with the general term
signify the rectangular summation of all matrix elements of a summation matrix with the general term ![]() in
in ![]() and
and![]() .
.
For instance,
![]() (17)
(17)
as each deterministic and random wave group is composed of M waves. Therefore, elements of summation matrices (13)-(16) are double sums of rectangular summation matrices of size![]() .
.
Secondly, we decompose ![]() (13) in diagonal and triangular matrices as
(13) in diagonal and triangular matrices as
![]() (18)
(18)
where
![]() (19)
(19)
is a diagonal matrix (9) of [2] in deterministic wave groups with![]() , which includes all diagonal elements of
, which includes all diagonal elements of![]() , and
, and
![]() (20)
(20)
is a complementary matrix (10) of [2] in deterministic wave groups with ![]() and
and![]() , which is composed of the upper and lower triangular matrices of
, which is composed of the upper and lower triangular matrices of![]() , respectively, since the first index of the dot product is a counter of rows and the second index is a counter of columns.
, respectively, since the first index of the dot product is a counter of rows and the second index is a counter of columns.
The kinetic energy of the deterministic flow is correspondingly expanded as
![]() (21)
(21)
where the first sum ![]() is produced by the elements of
is produced by the elements of![]() , i.e.
, i.e.
![]() (22)
(22)
and the second sum ![]() by the elements of
by the elements of![]() , viz.
, viz.
![]() (23)
(23)
In (22)-(23), the general term of ![]() is
is
![]() (24)
(24)
for![]() ,
, ![]() ,
, ![]() , and the general term of
, and the general term of ![]() is
is
![]() (25)
(25)
for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
Thirdly, we combine ![]() (14) and
(14) and ![]() (15) in deterministic and random wave groups as rectangular matrices
(15) in deterministic and random wave groups as rectangular matrices
![]() (26)
(26)
The kinetic energy of the deterministic-random flow is consequently decomposed in the following form:
![]() (27)
(27)
with the sum of elements of ![]() and
and![]() , viz.
, viz.
![]() (28)
(28)
where the general term of ![]() is
is
![]() (29)
(29)
for![]() ,
, ![]() ,
, ![]() , and
, and![]() . Here, identity
. Here, identity ![]() is used to convert (29) to the representation of (25).
is used to convert (29) to the representation of (25).
Fourthly, we expand ![]() (16) in random wave groups as follows:
(16) in random wave groups as follows:
![]() (30)
(30)
where
![]() (31)
(31)
is the diagonal matrix in random wave groups for![]() , which contains all diagonal elements of
, which contains all diagonal elements of![]() , and
, and
![]() (32)
(32)
is the complementary matrix in random wave groups for ![]() and
and![]() , which is constructed of the upper and lower triangular matrices of
, which is constructed of the upper and lower triangular matrices of![]() .
.
Thus, the kinetic energy of the random flow is decomposed as
![]() (33)
(33)
where the first sum ![]() is generated by the elements of
is generated by the elements of ![]() as
as
![]() (34)
(34)
and the second sum ![]() by the elements of
by the elements of ![]() since
since
![]() (35)
(35)
In Equations (34)-(35), the general term of ![]() becomes
becomes
![]() (36)
(36)
for![]() ,
, ![]() ,
, ![]() , and the general term of
, and the general term of ![]() takes the following form:
takes the following form:
![]() (37)
(37)
for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
Summation matrices ![]() (13),
(13), ![]() (14),
(14), ![]() (15), and
(15), and ![]() (16) of the kinetic energy (9) of the turbulent flow are visualized in Figure 1. Interchange of group indices
(16) of the kinetic energy (9) of the turbulent flow are visualized in Figure 1. Interchange of group indices ![]() describes transposition of elements of all four matrices with respect to local group diagonals
describes transposition of elements of all four matrices with respect to local group diagonals ![]() shown for matrix elements
shown for matrix elements ![]() and
and![]() ,
, ![]() and
and![]() ,
,![]() and
and![]() ,
, ![]() and
and![]() .
.
In Figure 1(a), the general term ![]() in (24) of
in (24) of ![]() (19) sums up diagonal elements of
(19) sums up diagonal elements of ![]() (18), the first general term
(18), the first general term ![]() in (25) of
in (25) of ![]() (20) sums up by rows elements of the upper triangular matrix of
(20) sums up by rows elements of the upper triangular matrix of![]() , and the second general term
, and the second general term ![]() sums up by columns elements of the lower triangular matrix of
sums up by columns elements of the lower triangular matrix of![]() .
.
In Figure 1(b) and Figure 1(c), the first general term ![]() in (29) of
in (29) of ![]() (26) sums up by rows all elements of matrix
(26) sums up by rows all elements of matrix ![]() (14), and the second general term
(14), and the second general term ![]() in (29) of
in (29) of ![]() sums up by columns all elements of matrix of
sums up by columns all elements of matrix of ![]() (15).
(15).
In Figure 1(d), the general term ![]() in (36) of
in (36) of ![]() (31) sums up diagonal elements of
(31) sums up diagonal elements of ![]() (16), the first general term
(16), the first general term ![]() in (37) of
in (37) of ![]() (32) sums up by rows elements of the upper triangular matrix of
(32) sums up by rows elements of the upper triangular matrix of![]() , and the second general term
, and the second general term ![]() sums up by columns elements of the lower triangular matrix of
sums up by columns elements of the lower triangular matrix of![]() .
.
Then rectangular sums are expanded into internal wave sums with ![]() (a local wave diagonal), which correspond to internal interaction of dpe-oscillons (125) or rpe-oscillons (155) from the mth family, and external wave sums with
(a local wave diagonal), which correspond to internal interaction of dpe-oscillons (125) or rpe-oscillons (155) from the mth family, and external wave sums with![]() , which describe external interaction of the dpe-oscillons or the rpe-oscillons from the mth and nth families.
, which describe external interaction of the dpe-oscillons or the rpe-oscillons from the mth and nth families.
Fifthly, we expand deterministic rectangular sums (24)-(25) into the internal and external sums. The summation matrix of the diagonal general term ![]() (24) of
(24) of ![]() (22)
(22)
![]() (38)
(38)
due to the commutative property of the dot products
![]() (39)
(39)
![]()
Figure 1. The summation matrices (13), (14), (15), and (16) of the turbulent kinetic energy (9) are shown by (a), (b), (c), and (d), respectively.
yields the following reduction of the rectangular summation to the diagonal and triangular summations (for the eDVK structures, see (18)-(19) of [2] ):
![]() (40)
(40)
where![]() .
.
The summation matrices of the non-diagonal general term ![]() (25) of
(25) of ![]() (23)
(23)
![]() (41)
(41)
because of the commutative properties of the dot products
![]() (42)
(42)
produce the following reduction of the rectangular summation to the diagonal and triangular summations (for the eDVK structures, see (23)-(24) of [2] ):
![]() (43)
(43)
where ![]() and
and![]() . If
. If![]() , the asymmetric reduction (43) is converted into the symmetric reduction (40).
, the asymmetric reduction (43) is converted into the symmetric reduction (40).
Sixthly, the summation matrices of the deterministic-random general term ![]() (29) of
(29) of ![]() (28)
(28)
![]() (44)
(44)
in the view of the commutative properties of the dot products
![]() (45)
(45)
return the following reduction of the rectangular summation to the diagonal and triangular summations:
![]() (46)
(46)
where ![]() and
and![]() .
.
Seventhly, we expand random rectangular sums (36)-(37) into the internal and external sums. The summation matrix of the diagonal general term ![]() (36) of
(36) of ![]() (34)
(34)
![]() (47)
(47)
in accordance with the commutative property of the dot products
![]() (48)
(48)
gives the following reduction of the rectangular summation to the diagonal and triangular summations (179) of [4] :
![]() (49)
(49)
where![]() .
.
The summation matrices of the non-diagonal general term ![]() (37) of
(37) of ![]() (35)
(35)
![]() (50)
(50)
in agreement with the commutative properties of the dot products
![]() (51)
(51)
return the following reduction of the rectangular summation to the diagonal and triangular summations (182) of [4] :
![]() (52)
(52)
where ![]() and
and![]() . If
. If![]() , the asymmetric expansion (52) is transformed into the symmetric expansion (49).
, the asymmetric expansion (52) is transformed into the symmetric expansion (49).
3. The Deterministic, Wave, Group, and Energy Pulsons
We now define the deterministic, wave, group, and energy pulsons and oscillons using various combinations of dot products of the tDVK structures and represent the dot products in terms of the tDDSD and eDDSD structures.
The general term of internal sum of (40) produces the deterministic, wave pulson of propagation of the deterministic velocity field (the dw-pulson for brevity)
![]() (53)
(53)
which describes vector self-interaction of the velocity field ![]() of the mth dpe-oscillon (125) from the selfsame ith deterministic wave group for
of the mth dpe-oscillon (125) from the selfsame ith deterministic wave group for ![]() and
and![]() .
.
Since the tDVK structure is related with the tDSK structures by (50) of [5]
![]() (54)
(54)
the dw-pulson in the tDDSD structures takes the following form:
![]() (55)
(55)
A superposition of a group of the dw-pulsons in the eDDSD structures
![]() (56)
(56)
is termed the deterministic, group pulson (the dg-pulson for conciseness). Here, ![]() is simplified by the Pythagorean identity for deterministic wave numbers
is simplified by the Pythagorean identity for deterministic wave numbers
![]() (57)
(57)
the definitions of the tDSK structures (1) of [5] , the eDSK structures (127), and the 3-v eDSK functions (128)-(130).
Eventually, the diagonal summation of all dg-pulsons results in the deterministic, kinetic-energy pulson (the dk-pulson for briefness)
![]() (58)
(58)
which shows a cumulative kinetic energy of M dg-pulsons.
4. The Deterministic, Diagonal, Wave, Group, and Energy Oscillons
The general term of external sum of (40) corresponds to the deterministic, diagonal, wave oscillon (the ddw-oscillon for shortness)
![]() (59)
(59)
which expresses vector external interaction of the velocity fields ![]() and
and ![]() of the distinct mth and nth dpe-oscillons (125) from the selfsame ith deterministic wave group for
of the distinct mth and nth dpe-oscillons (125) from the selfsame ith deterministic wave group for![]() ,
, ![]() , and
, and ![]() .
.
Using (54) and Equation (54) with ![]()
![]() (60)
(60)
we obtain the ddw-oscillon in the tDDSD structures
![]() (61)
(61)
Summation of (61) yields the deterministic, diagonal, group oscillon (the ddg-oscillon for concision) in the eDDSD structures
![]() (62)
(62)
where a nonlinear amplitude
![]() (63)
(63)
is produced by the deterministic wave numbers.
The triangular summation of the ddg-oscillons results in the deterministic, diagonal, kinetic-energy oscillon (the ddk-oscillon for pithiness)
![]() (64)
(64)
which gives an accumulative kinetic energy of ![]() ddg-oscillons.
ddg-oscillons.
So, summation of the diagonal constituents ![]() (22) of the kinetic energy
(22) of the kinetic energy ![]() is completed with the following result:
is completed with the following result:
![]() (65)
(65)
If![]() , then the ddw-oscillon (61) is converted into the doubled dw-pulson (55). Namely,
, then the ddw-oscillon (61) is converted into the doubled dw-pulson (55). Namely,
![]() (66)
(66)
Analogously, the ddg-oscillon (62) becomes equal to the doubled dg-pulson (56)
![]() (67)
(67)
since
![]() (68)
(68)
5. The Deterministic, Internal, Wave, Group, and Energy Oscillons
The general term of internal sum of (43) produces the deterministic, internal, wave oscillon (the diw-oscillon for terseness)
![]() (69)
(69)
which represents vector internal interaction of the velocity fields ![]() and
and ![]() of the mth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for
of the mth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() , and
, and![]() .
.
In the tDDSD structures, the diw-oscillon becomes
![]() (70)
(70)
Adding the diw-oscillons, we get the deterministic, internal, group oscillon (the dig-oscillon for curtness) in the eDDSD structures
![]() (71)
(71)
The diagonal summation of the dig-oscillons results in the deterministic, internal, kinetic-energy oscillon (the dik-oscillon for quickness)
![]() (72)
(72)
which returns a collective kinetic energy of M dig-oscillons.
6. The Deterministic, External, Wave, Group, and Energy Oscillons
The general term of external sum of (43) describes the deterministic, external, wave oscillon (the dew-oscillon for swiftness)
![]() (73)
(73)
which exposes vector external interaction of the velocity fields ![]() and
and![]() ,
, ![]() of the distinct mth and nth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for
of the distinct mth and nth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() ,
,![]() , and
, and![]() .
.
Using (54) and (60), we compute the dew-oscillon via the tDDSD structures
![]() (74)
(74)
The deterministic, external, group oscillon (the deg-oscillon for fastness) takes the following form in terms of the eDDSD structures:
![]() (75)
(75)
where nonlinear amplitudes
![]() (76)
(76)
are generated by the deterministic wave numbers.
We then imply the triangular summation of the deg-oscillons to find the deterministic, external, kinetic-energy oscillon (the dek-oscillon for simplicity)
![]() (77)
(77)
which demonstrates an aggregate kinetic energy of ![]() deg-oscillons.
deg-oscillons.
Thus, summation of the non-diagonal constituents ![]() (23) of the kinetic energy
(23) of the kinetic energy ![]() is finished as follows:
is finished as follows:
![]() (78)
(78)
If![]() , then the dew-oscillon (74) is transformed into the doubled diw-oscillon (70). Explicitly,
, then the dew-oscillon (74) is transformed into the doubled diw-oscillon (70). Explicitly,
![]() (79)
(79)
Similarly, the deg-oscillon (75) becomes equal to the doubled dig-oscillon (71), i.e.
![]() (80)
(80)
since
![]() (81)
(81)
7. The Deterministic-Random, Internal, Wave, Group, and Energy Oscillons
We then treat the deterministic-random, wave, group, and energy oscillons in terms of different combinations of dot products of the tDVK and tRVK structures and express the dot products in terms of the tDRSD, tRDSD, eDRSD, and eRDSD structures.
The general term of internal sum of (46) specifies the deterministic-random, internal, wave oscillon (the driw-oscillon for straightforwardness)
![]() (82)
(82)
which describes vector internal interaction of the velocity fields ![]() and
and ![]() of the mth dpe-oscillon (125) and the mth rpe-oscillon (155) from all ith deterministic and jth random wave groups for
of the mth dpe-oscillon (125) and the mth rpe-oscillon (155) from all ith deterministic and jth random wave groups for![]() ,
, ![]() , and
, and![]() .
.
In the tDRSD structures, the driw-oscillon is displayed by
![]() (83)
(83)
Adding the driw-oscillons, we obtain the deterministic-random, internal, group oscillon (the drig-oscillon for easiness) in the eDRSD structures
![]() (84)
(84)
where nonlinear amplitudes
![]() (85)
(85)
are produced by the deterministic and random wave numbers.
The diagonal summation of the drig-oscillons yields the deterministic-random, internal, kinetic-energy oscillon (the drik-oscillon for brevity)
![]() (86)
(86)
which reflects an amassed kinetic energy of M drig-group oscillons.
8. The Deterministic-Random, External, Wave, Group, and Energy Oscillons
The general term of external sum of (46) presents the deterministic-random, external, wave oscillon (the drew-oscillon for conciseness)
![]() (87)
(87)
which manifests vector external interaction of the velocity fields ![]() and
and![]() ,
, ![]() of the distinct mth and nth dpe-oscillons (125) with the distinct nth and mth rpe-oscillons (155) from all ith deterministic and jth random wave groups for
of the distinct mth and nth dpe-oscillons (125) with the distinct nth and mth rpe-oscillons (155) from all ith deterministic and jth random wave groups for![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
In the tDRSD and tRDSD structures, the drew-oscillon is specified as follows:
![]() (88)
(88)
Summation of the drew-oscillons gives the deterministic-random, external, group oscillon (the dreg-oscillon for briefness) in the eDRSD and eRDSD structures
![]()
![]() (89)
(89)
where nonlinear amplitudes
![]() (90)
(90)
and
![]() (91)
(91)
are generated by the deterministic and random wave numbers.
We then apply the triangular summation of the dreg-oscillons to get the deterministic-random, external, kinetic-energy oscillon (the drek-oscillon for shortness)
![]() (92)
(92)
which evaluates a total kinetic energy of ![]() dreg-oscillons.
dreg-oscillons.
If![]() , then the drew-wave oscillon (88) is converted into the doubled driw-oscillon (83). Namely,
, then the drew-wave oscillon (88) is converted into the doubled driw-oscillon (83). Namely,
![]() (93)
(93)
In the same way, the dreg-oscillon (89) is transformed into the doubled drig-oscillon (84), viz.
![]() (94)
(94)
because
![]() (95)
(95)
9. The Random, Wave, Group, and Energy Pulsons
We proceed with the random, wave, group, and energy pulsons and oscillons via diverse combinations of dot products of the tRVK structures and display the dot products in terms of the tRRSD and eRRSD structures.
The general term of internal sum of (49) corresponds to the random, wave pulson of propagation of the random velocity field (183) of [4] (the rw-pulson for concision)
![]() (96)
(96)
which expresses vector self-interaction of the velocity field ![]() of the mth rpe-oscillon (155) from the selfsame ith random wave group for
of the mth rpe-oscillon (155) from the selfsame ith random wave group for ![]() and
and![]() .
.
As the tRVK structure is connected with the tRSK structures with the help of (30) of [4]
![]() (97)
(97)
the rw-pulson in the tRRSD structures may be represented as follows:
![]() (98)
(98)
A superposition of a group of the rw-pulsons in the eRRSD structures
![]() (99)
(99)
is called the random, group pulson (the rg-pulson for pithiness), whereas ![]() is simplified by the Pythagorean identity for random wave numbers
is simplified by the Pythagorean identity for random wave numbers
![]() (100)
(100)
the definitions of tRSK structures (1) of [4] , the eRSK structures (157), and the 3-v eRSK functions (158)-(162).
Finally, the diagonal summation of all rg-pulsons produces the random, kinetic-energy pulson (the rk-pulson for terseness)
![]() (101)
(101)
which evaluates an entire kinetic energy of M rg-pulsons.
10. The Random, Diagonal, Wave, Group, and Energy Oscillons
The general term of external sum of (49) determines the random, diagonal, wave oscillon (187) of [4] (the rdw-oscillon for curtness)
![]() (102)
(102)
which describes vector external interaction of the velocity fields ![]() and
and ![]() of the distinct mth and nth rpe-oscillons (155) from the selfsame ith random wave group for
of the distinct mth and nth rpe-oscillons (155) from the selfsame ith random wave group for![]() ,
, ![]() , and
, and![]() .
.
With the help of (97) and Equation (97) with ![]()
![]() (103)
(103)
we find the rdw-oscillon in the tRRSD structures
![]() (104)
(104)
We then sum up (104) in wave groups to compute the random, diagonal, group oscillon (the rdg-oscillon for quickness) in the eRRSD structures
![]() (105)
(105)
where
![]() (106)
(106)
is a nonlinear amplitude, which depends on the random wave numbers.
The triangular summation of the rdg-oscillons returns the random, diagonal, kinetic-energy oscillon (the rdk-oscillon for swiftness)
![]() (107)
(107)
which yields a whole kinetic energy of ![]() rdg-oscillons.
rdg-oscillons.
Consequently, summation of the diagonal constituents ![]() (34) of the kinetic energy
(34) of the kinetic energy ![]() is finished as follows:
is finished as follows:
![]() (108)
(108)
If![]() , then the rdw-oscillon (104) is transformed into the doubled rw-pulson (98). Explicitly,
, then the rdw-oscillon (104) is transformed into the doubled rw-pulson (98). Explicitly,
![]() (109)
(109)
Similarly, the rdg-oscillon (105) is equivalent to the doubled rg-pulson (99)
![]() (110)
(110)
as
![]() (111)
(111)
11. The Random, Internal, Wave, Group, and Energy Oscillons
The general term of internal sum of (52) defines the random, internal, wave oscillon (196) of [4] (the riw-oscillon for fastness)
![]() (112)
(112)
which expresses vector internal interaction of the velocity fields ![]() and
and ![]() of the mth rpe-oscillons (155) from the distinct ith and jth random wave groups for
of the mth rpe-oscillons (155) from the distinct ith and jth random wave groups for![]() ,
, ![]() , and
, and![]() .
.
The riw-oscillon may be written in the tRRSD structures as
![]() (113)
(113)
Addition of the riw-oscillons gives the random, internal, group oscillon (the rig-oscillon for simplicity) in the eRRSD structures
![]() (114)
(114)
Eventually, we sum up the rig-oscillons to calculate the random, internal, kinetic-energy oscillon (the rik-oscillon for straightforwardness)
![]() (115)
(115)
which expresses an overall kinetic energy of M rig-oscillons.
12. The Random, External, Wave, Group, and Energy Oscillons
The general term of external sum of (52) sets up the random, external, wave oscillon (200) of [4] (the rew-oscillon for easiness)
![]() (116)
(116)
which specifies vector external interaction of the velocity fields ![]() and
and![]() ,
, ![]() of the distinct mth and nth rpe-oscillons (155) from the distinct ith and jth random wave groups for
of the distinct mth and nth rpe-oscillons (155) from the distinct ith and jth random wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
In accordance with (97) and (103), computation of the rew-oscillon in terms of the tRRSD structures gives
![]() (117)
(117)
The random, external, group oscillon (the reg-oscillon for brevity) via the eRRSD structures may be represented as follows:
![]() (118)
(118)
where
![]() (119)
(119)
are nonlinear amplitudes, which are produced by the random wave numbers.
Usage of the triangular summation of the reg-oscillons results in the random, external, kinetic-energy oscillon (the rek-oscillon for conciseness)
![]() (120)
(120)
which describes a full kinetic energy of ![]() reg-oscillons.
reg-oscillons.
So, summation of the non-diagonal constituents ![]() (35) of the kinetic energy
(35) of the kinetic energy ![]() is accomplished by
is accomplished by
![]() (121)
(121)
If![]() , then the rew-oscillon (117) is converted into the doubled riw-oscillon (113). Namely,
, then the rew-oscillon (117) is converted into the doubled riw-oscillon (113). Namely,
![]() (122)
(122)
Analogously, the reg-oscillon (118) is identical to the doubled rig-oscillon (114), viz.
![]() (123)
(123)
due to the following relations:
![]() (124)
(124)
13. The Deterministic Elementary Oscillons and Pulsons
The mth deterministic, velocity-potential, elementary oscillon of propagation of the deterministic velocity potential ![]() (the dpe-oscillon for briefness) from the selfsame ith deterministic wave group is defined by
(the dpe-oscillon for briefness) from the selfsame ith deterministic wave group is defined by
![]() (125)
(125)
where ![]() and
and![]() .
.
Explicitly, four dpe-oscillons of the mth family
![]() (126)
(126)
are specified via the eDSK structures (3) of [5]
![]() (127)
(127)
where ![]() are functional amplitudes of a deterministic harmonic variable
are functional amplitudes of a deterministic harmonic variable![]() , 3-v (three-variables) eDSK functions
, 3-v (three-variables) eDSK functions ![]() are products
are products
![]() (128)
(128)
of the 1-v (one-variable) eDSK functions![]() ,
, ![]() , and
, and![]() :
:
![]() (129)
(129)
where ![]() and
and ![]() are two-variables (2-v) deterministic propagation variables computed by
are two-variables (2-v) deterministic propagation variables computed by
![]() (130)
(130)
In Equations (125)-(130), ![]() is the Cartesian coordinate of a motionless frame of reference, t is time,
is the Cartesian coordinate of a motionless frame of reference, t is time, ![]() is the Cartesian coordinate of a frame of reference moving with the mth dpe-oscillon,
is the Cartesian coordinate of a frame of reference moving with the mth dpe-oscillon, ![]() is the celerity of propagation of the mth dpe-oscillon, and
is the celerity of propagation of the mth dpe-oscillon, and ![]() is a reference value of
is a reference value of ![]() at
at![]() ,
, ![]() are the wave numbers of the mth dpe-oscillon in the x-,y-,z-directions, and a sign parameter
are the wave numbers of the mth dpe-oscillon in the x-,y-,z-directions, and a sign parameter ![]() for
for ![]() and
and ![]() for
for![]() .
.
A deterministic, velocity-potential, wave oscillon (a dpw-oscillon for shortness)
![]() (131)
(131)
contains I dpe-oscillons.
Similarly, a deterministic, velocity-potential, group oscillon (a dpg-oscillon for concision)
![]() (132)
(132)
is composed of M dpw-oscillons. The dpg-oscillon describes propagation of the scalar Helmholtz potential of the deterministic velocity field (183) of [5] .
In the tDDSD structures, the deterministic, elementary pulson of propagation of the deterministic velocity potential (the de-pulson for pithiness) is set by
![]() (133)
(133)
The de-pulson (133) describes scalar self-interaction of the velocity potential ![]() of the selfsame mth dpe-oscillon (125) from the selfsame ith deterministic wave group for
of the selfsame mth dpe-oscillon (125) from the selfsame ith deterministic wave group for ![]() and
and![]() .
.
In the eDDSD structures, the de-pulsons become
![]() (134)
(134)
For ![]() and
and![]() , the dw-pulson (55) takes in the eDDSD structures the following forms:
, the dw-pulson (55) takes in the eDDSD structures the following forms:
![]() (135)
(135)
The dw-pulsons (135) and the dg-pulson (56) then become the following superpositions of the de-pulsons (134):
![]() (136)
(136)
and
![]() (137)
(137)
where![]() .
.
In the tDDSD structures, the deterministic, internal, elementary oscillon (the die-oscillon for terseness) is specified by
![]() (138)
(138)
The die-oscillon (138) represents scalar internal interaction of the velocity potentials ![]() and
and ![]() of the mth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for
of the mth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() , and
, and![]() .
.
In the eDDSD structures, there are six die-oscillons
![]() (139)
(139)
For![]() ,
, ![]() , and
, and![]() , the diw-oscillon (70) may be written in the eDDSD structures as follows:
, the diw-oscillon (70) may be written in the eDDSD structures as follows:
![]() (140)
(140)
The diw-oscillons (140) and the dig-oscillon (71) are decomposed via the die-oscillons (139) as follows:
![]() (141)
(141)
and
![]() , (142)
, (142)
where![]() .
.
In the tDDSD structures, the deterministic, diagonal, elementary oscillon (the dde-oscillon for curtness) is established by
![]() (143)
(143)
The dde-oscillon (143) manifests scalar external interaction of the velocity potentials ![]() and
and ![]() of the distinct mth and nth dpe-oscillons (125) from the selfsame ith deterministic wave group for
of the distinct mth and nth dpe-oscillons (125) from the selfsame ith deterministic wave group for![]() ,
, ![]() , and
, and![]() .
.
In the eDDSD structures, we get four dde-oscillons
![]() (144)
(144)
For![]() ,
, ![]() , and
, and![]() , the ddw-oscillon (61) in the eDDSD structures becomes
, the ddw-oscillon (61) in the eDDSD structures becomes
![]() (145)
(145)
The ddw-oscillons (145) and the ddg-oscillon (62) then are subsequent superpositions of the dde-oscillons (144):
![]() (146)
(146)
and
![]() (147)
(147)
where ![]() and
and![]() .
.
In the tDDSD structures, the deterministic, external, elementary oscillon (the dee-oscillon for quickness) is set by
![]() (148)
(148)
The dee-oscillon (148) expresses scalar external interaction of the velocity potentials ![]() and
and ![]() of the distinct mth and nth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for
of the distinct mth and nth dpe-oscillons (125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
In the eDDSD structures, we have six dee-oscillons
![]() (149)
(149)
For![]() ,
,![]() ,
, ![]() , and
, and ![]() , the dew-oscillon (74) may be represented via the eDDSD structures in the following forms:
, the dew-oscillon (74) may be represented via the eDDSD structures in the following forms:
![]()
![]() (150)
(150)
![]()
The dew-oscillons (150) and the deg-oscillon (75) are expanded in the dee-oscillons (149) in the following way:
![]() (151)
(151)
and
![]() (152)
(152)
where![]() ,
, ![]() , and the nonlinear amplitudes are specified by (76).
, and the nonlinear amplitudes are specified by (76).
If![]() , then the dde-oscillons (143)-(144) are reduced to the doubled de-pulsons (133)-(134), i.e.
, then the dde-oscillons (143)-(144) are reduced to the doubled de-pulsons (133)-(134), i.e.
![]() (153)
(153)
In the similar way, the dee-oscillons (148)-(149) are transformed into the doubled die-oscillons (138)-(139). Namely,
![]() (154)
(154)
14. The Random Elementary Oscillons and Pulsons
The mth random, velocity-potential, elementary oscillon of propagation of the random velocity potential ![]() (209) of [4] (the rpe-oscillon for swiftness) from the selfsame ith random wave group is specified by
(209) of [4] (the rpe-oscillon for swiftness) from the selfsame ith random wave group is specified by
![]() (155)
(155)
where ![]() and
and![]() .
.
Namely, four rpe-oscillons of the mth family
![]() (156)
(156)
are expressed via the eRSK structures (3) of [4]
![]() (157)
(157)
where ![]() are functional amplitudes of a random harmonic variable
are functional amplitudes of a random harmonic variable![]() , 3-v eRSK
, 3-v eRSK ![]() are products
are products
![]() (158)
(158)
of the 1-v eRSK functions![]() ,
, ![]() , and
, and ![]() :
:
![]() (159)
(159)
where ![]() and
and ![]() are 2-v random propagation variables determined by
are 2-v random propagation variables determined by
![]() (160)
(160)
In Equations (155)-(160), ![]() is the Cartesian coordinate of a frame of reference moving with the mth rpe-oscillon,
is the Cartesian coordinate of a frame of reference moving with the mth rpe-oscillon, ![]() is the celerity of propagation of the mth rpe-oscillon, and
is the celerity of propagation of the mth rpe-oscillon, and ![]() is a reference value of
is a reference value of ![]() at
at![]() . Wave parameters
. Wave parameters
![]() (161)
(161)
together with functional amplitudes
![]() (162)
(162)
are smooth random functions of time from C∞. The wave numbers ![]() of the mth rpe-oscillon in the x-,y-,z-directions are random constants since otherwise the temporal derivative of the velocity potential does not commutate with the gradient.
of the mth rpe-oscillon in the x-,y-,z-directions are random constants since otherwise the temporal derivative of the velocity potential does not commutate with the gradient.
A random, velocity-potential, wave oscillon (a rpw-oscillon for fastness)
![]() (163)
(163)
is composed of I rpe-oscillons.
Analogously, a random, velocity-potential, group oscillon (a rpg-oscillon for simplicity)
![]() (164)
(164)
consists of M rpw-oscillons. The rpg-oscillon describes propagation of the scalar Helmholtz potential of the random velocity field (95) of [4] .
In the tRRSD structures, the random, elementary pulson of propagation of the random velocity potential (213) of [4] (the re-pulson for easiness) is determined by
![]() (165)
(165)
The re-pulson (165) specifies scalar self-interaction of the velocity potential ![]() of the selfsame mth rpe-oscillon (155) from the selfsame ith random wave group for
of the selfsame mth rpe-oscillon (155) from the selfsame ith random wave group for ![]() and
and![]() .
.
The re-pulsons may be represented in the eRRSD structures as follows:
![]() (166)
(166)
For ![]() and
and![]() , the rw-pulson (98) is expressed in terms of the eRRSD structures through the following forms:
, the rw-pulson (98) is expressed in terms of the eRRSD structures through the following forms:
![]() (167)
(167)
The rw-pulsons (167) and the rg-pulson (99) may be displayed as the following superpositions of the re-pulsons (166):
![]() (168)
(168)
and
![]() (169)
(169)
where![]() .
.
In the tRRSD structures, the random, internal, elementary oscillon (218) of [4] (the rie-oscillon for straightforwardness) is defined by
![]() (170)
(170)
The rie-oscillon (170) corresponds to scalar internal interaction of the velocity potentials ![]() and
and ![]() of the mth rpe-oscillons (155) from the distinct ith and jth random wave groups for
of the mth rpe-oscillons (155) from the distinct ith and jth random wave groups for![]() ,
, ![]() , and
, and ![]() .
.
There are six rie-oscillons in the eRRSD structures. Namely,
![]() (171)
(171)
For![]() ,
, ![]() , and
, and![]() , the riw-oscillon (113) may be expressed in the eRRSD structures as follows:
, the riw-oscillon (113) may be expressed in the eRRSD structures as follows:
![]() (172)
(172)
The riw-oscillons (172) and the rig-oscillon (114) are expanded in terms of the rie-oscillons (171) in the following form:
![]() (173)
(173)
and
![]() (174)
(174)
where![]() .
.
In the tRRSD structures, the random, diagonal, elementary oscillon (223) of [4] (the rde-oscillon for brevity) is set by
![]() (175)
(175)
The rde-oscillon (175) designates scalar external interaction of the velocity potentials ![]() and
and ![]() of the distinct mth and nth rpe-oscillons (155) from the selfsame ith random wave group for
of the distinct mth and nth rpe-oscillons (155) from the selfsame ith random wave group for![]() ,
, ![]() , and
, and ![]() .
.
In the eRRSD structures, we have four rde-oscillons
![]() (176)
(176)
For![]() ,
, ![]() , and
, and![]() , the rdw-oscillon (104) is specified in the tRRSD structures by
, the rdw-oscillon (104) is specified in the tRRSD structures by
![]() (177)
(177)
The rdw-oscillons (177) and the rdg-oscillon (105) then are the following superpositions of the rde-oscillons (176):
![]() (178)
(178)
and
![]() (179)
(179)
where ![]() and
and![]() .
.
In the tRRSD structures, the random, external, elementary oscillon (228) of [4] (the ree-oscillon for conciseness) is established by
![]() (180)
(180)
The ree-oscillon (180) represents scalar external interaction of the velocity potentials ![]() and
and ![]() of the distinct mth and nth rpe-oscillons (155) from the distinct ith and jth random wave groups for
of the distinct mth and nth rpe-oscillons (155) from the distinct ith and jth random wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
In terms of the eRRSD structures, we get six ree-oscillons
![]() (181)
(181)
For![]() ,
, ![]() ,
, ![]() , and
, and ![]() , the rew-oscillon (117) may be written via the eRRSD structures as follows:
, the rew-oscillon (117) may be written via the eRRSD structures as follows:
![]()
![]() (182)
(182)
![]()
The rew-oscillons (182) and the reg-oscillon (118) are expressed via the ree-oscillons (181) as
![]() (183)
(183)
and
![]() (184)
(184)
where![]() ,
, ![]() , and the nonlinear amplitudes are given by (119).
, and the nonlinear amplitudes are given by (119).
If![]() , then the rde-oscillons (175)-(176) are converted into the doubled re-pulsons (165)-(166), viz.
, then the rde-oscillons (175)-(176) are converted into the doubled re-pulsons (165)-(166), viz.
![]() (185)
(185)
Analogously, the ree-oscillons (180)-(181) are reduced to the doubled rie-oscillons (170)-(171). Explicitly,
![]() (186)
(186)
15. The Deterministic-Random and Random-Deterministic Elementary Oscillons
In the tDRSD structures, the deterministic-random, internal, elementary oscillon (the drie-oscillon for briefness) is specified by
![]() (187)
(187)
The drie-oscillon (187) describes scalar internal interaction of the velocity potentials ![]() and
and ![]() of the mth dpe-oscillon (125) and the mth rpe-oscillon (155) from all ith deterministic and jth random wave groups for
of the mth dpe-oscillon (125) and the mth rpe-oscillon (155) from all ith deterministic and jth random wave groups for![]() ,
, ![]() , and
, and![]() .
.
In the eDRSD structures, there are 16 drie-oscillons
![]() (188)
(188)
For![]() ,
, ![]() , and
, and![]() , the driw-oscillon (83) in the eDRSD structures becomes
, the driw-oscillon (83) in the eDRSD structures becomes
![]() (189)
(189)
The driw-oscillons (189) and the drig-oscillon (84) are represented via the drie-oscillons (188) in the following form:
![]() (190)
(190)
and
![]() (191)
(191)
where ![]() and the nonlinear amplitudes are provided by (85).
and the nonlinear amplitudes are provided by (85).
In the tDRSD structures, the deterministic-random, external, elementary oscillon (the dree-oscillon for shortness) is set by
![]() (192)
(192)
The dree-oscillon (192) reflects scalar external interaction of the velocity potentials ![]() and
and ![]() of the distinct mth dpe-oscillon (125) and the nth rpe-oscillon (155) from all ith deterministic and jth random wave groups for
of the distinct mth dpe-oscillon (125) and the nth rpe-oscillon (155) from all ith deterministic and jth random wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
The random-deterministic, external, elementary oscillon (the rdee-oscillon for concision) in the tRDSD structures is defined by
![]() (193)
(193)
The rdee-oscillon (193) describes scalar external interaction of the velocity potentials ![]() and
and ![]() of the distinct mth rpe-oscillon (155) and the nth dpe-oscillon (125) from all jth random and ith deterministic wave groups for
of the distinct mth rpe-oscillon (155) and the nth dpe-oscillon (125) from all jth random and ith deterministic wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
Via the eDRSD structures, we have 16 dree-oscillons
![]() (194)
(194)
In the eRDSD structures, there are also 16 rdee-oscillons
![]() (195)
(195)
With the help of the eDRSD and eRDSD structures, the drew-oscillon (88) for![]() ,
, ![]() ,
, ![]() , and
, and ![]() is specified in the following forms:
is specified in the following forms:
![]()
![]() (196)
(196)
![]()
The drew-wave oscillons (196) and the dreg-oscillon (89) are represented via the dree-oscillons (194) and rdee-oscillons (195) as follows:
![]()
![]() (197)
(197)
![]()
and
![]()
![]() (198)
(198)
where![]() ,
, ![]() , and the nonlinear amplitudes are specified by (90)-(91).
, and the nonlinear amplitudes are specified by (90)-(91).
Symbolic computation of exact expansions of the exponential oscillons and pulsons have been implemented with the help of experimental and theoretical programming in Maple. Maple codes will be published elsewhere because of their large size.
If![]() , then sum of the dree-oscillon (192) and the rdee-oscillon (193) is transformed into the doubled drie-oscillon (187). Namely,
, then sum of the dree-oscillon (192) and the rdee-oscillon (193) is transformed into the doubled drie-oscillon (187). Namely,
![]() (199)
(199)
The rectangular matrix of the dree-oscillons (194) and the rectangular matrix of the rdee-elementary oscillons (195) are composed of the same elements since,
![]() (200)
(200)
i.e. the upper triangular matrix of the dree-oscillons (194) is complemented by the upper triangular matrix of the rdee-oscillons (195) in the triangular summation of (92) to include all non-diagonal elements in![]() .
.
16. Conclusion
Finally, we summarize theoretical quantization of the turbulent kinetic energy of exact wave turbulence. The cumulative, kinetic-energy pulson (9) (the ck-pulson for simplicity) may be decomposed as follows:
![]() (201)
(201)
where ![]() is the dk-pulson (58) that is composed of M dg-pulsons
is the dk-pulson (58) that is composed of M dg-pulsons ![]() (56),
(56), ![]() is the dik-oscillon (72) that includes M dig-oscillons
is the dik-oscillon (72) that includes M dig-oscillons ![]() (71),
(71), ![]() is the drik-oscillon (86) that is constructed of M drig-oscillons
is the drik-oscillon (86) that is constructed of M drig-oscillons ![]() (84),
(84), ![]() is the rik-oscillon (115) that consists of M rig-oscillons
is the rik-oscillon (115) that consists of M rig-oscillons ![]() (114),
(114), ![]() is the rk-pulson (101) that encompasses M rg-pulsons
is the rk-pulson (101) that encompasses M rg-pulsons ![]() (99),
(99), ![]() is the ddk-oscillon (64) that comprises
is the ddk-oscillon (64) that comprises ![]() ddg-oscillons
ddg-oscillons ![]() (62),
(62), ![]() is the dek-oscillon (77) that encloses
is the dek-oscillon (77) that encloses ![]() deg-oscillons
deg-oscillons ![]() (75),
(75), ![]() is the drek-oscillon (92) that contains
is the drek-oscillon (92) that contains ![]() dreg-oscillons
dreg-oscillons ![]() (89),
(89), ![]() is the rek-oscillon (120) that incorporates
is the rek-oscillon (120) that incorporates ![]() reg-oscillons
reg-oscillons ![]() (118), and
(118), and ![]() is the rdk-oscillon (107) that embraces
is the rdk-oscillon (107) that embraces ![]() rdg-oscillons
rdg-oscillons ![]() (105).
(105).
The dg-pulson ![]() (56) is composed of I dw-pulsons
(56) is composed of I dw-pulsons ![]() (53) that describe vector self-interaction of the velocity field
(53) that describe vector self-interaction of the velocity field ![]() of the mth dpe-oscillon
of the mth dpe-oscillon ![]() (125) from the selfsame ith deterministic wave group for
(125) from the selfsame ith deterministic wave group for ![]() and
and![]() .
.
The dig-oscillon ![]() (71) consists of
(71) consists of ![]() diw-oscillons
diw-oscillons ![]() (69) that represent vector internal interaction of the velocity fields
(69) that represent vector internal interaction of the velocity fields ![]() and
and ![]() of the mth dpe-oscillons
of the mth dpe-oscillons ![]() and
and ![]() (125) from the distinct ith and jth deterministic wave groups for
(125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() , and
, and![]() .
.
The drig-oscillon ![]() (84) consists of
(84) consists of ![]() driw-oscillons
driw-oscillons ![]() (82) that describe vector internal interaction of the velocity fields
(82) that describe vector internal interaction of the velocity fields ![]() and
and ![]() of the mth dpe-oscillon
of the mth dpe-oscillon ![]() (125) and the mth rpe-oscillon
(125) and the mth rpe-oscillon ![]() (155) from all ith deterministic and jth random wave groups for
(155) from all ith deterministic and jth random wave groups for![]() ,
,![]() , and
, and![]() .
.
The rig-oscillon ![]() (114) includes
(114) includes ![]() riw-oscillons
riw-oscillons ![]() (112) that correspond to vector internal interaction of the velocity fields
(112) that correspond to vector internal interaction of the velocity fields ![]() and
and ![]() of the mth rpe-oscillons
of the mth rpe-oscillons ![]() and
and ![]() (155) from the distinct ith and jth random wave groups for
(155) from the distinct ith and jth random wave groups for![]() ,
, ![]() , and
, and![]() .
.
The rg-pulson ![]() (99) is constructed of I rw-pulsons
(99) is constructed of I rw-pulsons ![]() (96) that determine vector self-interaction of the velocity field
(96) that determine vector self-interaction of the velocity field ![]() of the mth rpe-oscillon
of the mth rpe-oscillon ![]() (155) from the selfsame ith random wave group for
(155) from the selfsame ith random wave group for ![]() and
and![]() .
.
The ddg-oscillon ![]() (62) is constructed of I ddw-oscillons
(62) is constructed of I ddw-oscillons ![]() (59) that express vector external interaction of the velocity fields
(59) that express vector external interaction of the velocity fields ![]() and
and ![]() of the distinct mth and nth dpe-oscillons
of the distinct mth and nth dpe-oscillons ![]() and
and ![]() (125) from the selfsame ith deterministic wave group for
(125) from the selfsame ith deterministic wave group for![]() ,
, ![]() ,
,![]() .
.
The deg-oscillon ![]() (75) includes
(75) includes ![]() dew-oscillons
dew-oscillons ![]() (73) that expose vector external interaction of the velocity fields
(73) that expose vector external interaction of the velocity fields ![]() and
and![]() ,
, ![]() of the distinct mth and nth dpe-oscillons
of the distinct mth and nth dpe-oscillons ![]() and
and ![]() (125) from the distinct ith and jth deterministic wave groups for
(125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
The dreg-oscillon ![]() (89) includes
(89) includes ![]() drew-oscillons
drew-oscillons ![]() (87) that express vector external interaction of the velocity fields
(87) that express vector external interaction of the velocity fields ![]() and
and![]() ,
, ![]() of the distinct mth and nth dpe-oscillons
of the distinct mth and nth dpe-oscillons ![]() and
and ![]() (125) with the distinct nth and mth rpe-oscillons
(125) with the distinct nth and mth rpe-oscillons ![]() and
and ![]() (155) from all ith deterministic and jth random wave groups for
(155) from all ith deterministic and jth random wave groups for![]() ,
,![]() ,
, ![]() , and
, and![]() .
.
The reg-group oscillon ![]() (118) consists of
(118) consists of ![]() rew-oscillons
rew-oscillons ![]() (116) that represent vector external interaction of the velocity fields
(116) that represent vector external interaction of the velocity fields![]() ,
,![]() and
and ![]() of the distinct mth and nth rpe-oscillons
of the distinct mth and nth rpe-oscillons ![]() and
and ![]() (155) from the distinct ith and jth random wave groups for
(155) from the distinct ith and jth random wave groups for![]() ,
,![]() ,
,![]() , and
, and![]() .
.
The rdg-oscillon ![]() (105) is composed of I rdw-oscillons
(105) is composed of I rdw-oscillons ![]() (102) that manifest vector external interaction of the velocity fields
(102) that manifest vector external interaction of the velocity fields ![]() and
and ![]() of the distinct mth and nth rpe-oscillons
of the distinct mth and nth rpe-oscillons ![]() and
and ![]() (155) from the selfsame ith random wave group for
(155) from the selfsame ith random wave group for![]() ,
,![]() , and
, and![]() .
.
The dw-pulsons ![]() (135) are composed of three of I de-pulsons
(135) are composed of three of I de-pulsons ![]() (134) that describe scalar self-interaction (133) of the velocity potential
(134) that describe scalar self-interaction (133) of the velocity potential ![]() of the selfsame mth dpe-oscillon
of the selfsame mth dpe-oscillon ![]() (125) from the selfsame ith deterministic wave groups for
(125) from the selfsame ith deterministic wave groups for ![]() and
and![]() .
.
The diw-oscillons ![]() (140) consist of two of
(140) consist of two of ![]() die-oscillons
die-oscillons ![]() (139) that represent scalar internal interaction (138) of the velocity potentials
(139) that represent scalar internal interaction (138) of the velocity potentials ![]() and
and ![]() of the mth dpe-oscillons
of the mth dpe-oscillons ![]() and
and ![]() (125) from the distinct ith and jth deterministic wave groups for
(125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() , and
, and![]() .
.
The driw-oscillons ![]() (189) are composed of three of
(189) are composed of three of ![]() drie-oscillons
drie-oscillons ![]() (188) that represent scalar internal interaction (187) of the velocity potentials
(188) that represent scalar internal interaction (187) of the velocity potentials ![]() and
and ![]() of the mth dpe-oscillon
of the mth dpe-oscillon ![]() (125) and the mth rpe-oscillon
(125) and the mth rpe-oscillon ![]() (155) from all ith deterministic and jth random wave groups for
(155) from all ith deterministic and jth random wave groups for![]() ,
,![]() , and
, and![]() .
.
The riw-oscillons ![]() (172) include two of
(172) include two of ![]() rie-oscillons
rie-oscillons ![]() (171) that correspond to scalar internal interaction (170) of the velocity potentials
(171) that correspond to scalar internal interaction (170) of the velocity potentials ![]() and
and ![]() of the mth rpe-oscillons
of the mth rpe-oscillons ![]() and
and ![]() (155) from the distinct ith and jth random wave groups for
(155) from the distinct ith and jth random wave groups for![]() ,
, ![]() , and
, and![]() .
.
The rw-pulsons ![]() (167) are constructed of three of I re-pulsons
(167) are constructed of three of I re-pulsons ![]() (166) that determine scalar self-interaction (165) of the velocity potential
(166) that determine scalar self-interaction (165) of the velocity potential ![]() of the selfsame mth rpe-oscillon
of the selfsame mth rpe-oscillon ![]() (155) from the selfsame ith random wave group for
(155) from the selfsame ith random wave group for ![]() and
and![]() .
.
The ddw-oscillons ![]() (145) are constructed of three of I dde-oscillons
(145) are constructed of three of I dde-oscillons ![]() (144) that express scalar external interaction (143) of the velocity potentials
(144) that express scalar external interaction (143) of the velocity potentials ![]() and
and ![]() of the distinct mth and nth dpe-oscillons
of the distinct mth and nth dpe-oscillons ![]() and
and ![]() (125) from the selfsame ith deterministic wave group for
(125) from the selfsame ith deterministic wave group for ![]() ,
, ![]() ,
,![]() .
.
The dew-oscillons ![]() (150) include two of
(150) include two of ![]() dee-oscillons
dee-oscillons ![]() (149) that expose scalar external interaction (148) of the velocity potentials
(149) that expose scalar external interaction (148) of the velocity potentials ![]() and
and ![]() of the distinct mth and nth dpe-oscillons
of the distinct mth and nth dpe-oscillons ![]() and
and ![]() (125) from the distinct ith and jth deterministic wave groups for
(125) from the distinct ith and jth deterministic wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
The drew-oscillons ![]() (196) include three of
(196) include three of ![]() dree-oscillons
dree-oscillons ![]() (194) and three of
(194) and three of ![]() rdee-oscillons
rdee-oscillons ![]() (195) that expose scalar external interaction (192) of the velocity potentials
(195) that expose scalar external interaction (192) of the velocity potentials ![]() and
and ![]() of the distinct mth dpe-oscillon
of the distinct mth dpe-oscillon ![]() (125) and the nth rpe-oscillon
(125) and the nth rpe-oscillon ![]() (155) from all ith deterministic and jth random wave groups and scalar external interaction (193) of the velocity potentials
(155) from all ith deterministic and jth random wave groups and scalar external interaction (193) of the velocity potentials ![]() and
and ![]() of the distinct mth rpe-oscillon
of the distinct mth rpe-oscillon ![]() (155) and nth dpe-oscillon
(155) and nth dpe-oscillon ![]() (125) from all jth random and ith deterministic wave groups for
(125) from all jth random and ith deterministic wave groups for![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
The rew-oscillons ![]() (182) consist of two of
(182) consist of two of ![]() ree-oscillons
ree-oscillons ![]() (181) that represent scalar external interaction (180) of the velocity potentials
(181) that represent scalar external interaction (180) of the velocity potentials ![]() and
and ![]() of the distinct mth and nth rpe-oscillons
of the distinct mth and nth rpe-oscillons ![]() and
and ![]() (155) from the distinct ith and jth random wave groups for
(155) from the distinct ith and jth random wave groups for![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The rdw-oscillons ![]() (177) are composed of three of I rde-oscillons
(177) are composed of three of I rde-oscillons ![]() (176) that manifest scalar external interaction (175) of the velocity potentials
(176) that manifest scalar external interaction (175) of the velocity potentials ![]() and
and ![]() of the distinct mth and nth rpe-oscillons
of the distinct mth and nth rpe-oscillons ![]() and
and ![]() (155) from the selfsame ith random wave group for
(155) from the selfsame ith random wave group for![]() ,
, ![]() , and
, and![]() .
.
The deterministic, vector, non-diagonal, external interaction for ![]() and
and ![]() is determined by the superposition of dot products
is determined by the superposition of dot products ![]() (73). Thus, the deterministic, vector, non-diagonal, internal interaction for
(73). Thus, the deterministic, vector, non-diagonal, internal interaction for ![]() and
and ![]() is specified by the single dot product
is specified by the single dot product ![]() (69) and the deterministic, vector, diagonal, external interaction for
(69) and the deterministic, vector, diagonal, external interaction for ![]() and
and ![]() is displayed by the single dot product
is displayed by the single dot product ![]() (59), as well. Eventually, the deterministic, vector, diagonal, internal interaction for
(59), as well. Eventually, the deterministic, vector, diagonal, internal interaction for ![]() and
and ![]() is also defined by the single dot product
is also defined by the single dot product ![]() (53).
(53).
The deterministic-random, vector, non-diagonal, external interaction for ![]() and
and ![]() is expressed by the superposition of dot products
is expressed by the superposition of dot products ![]() (87). Therefore, the deterministic-random, vector, non-diagonal, internal interaction for
(87). Therefore, the deterministic-random, vector, non-diagonal, internal interaction for ![]() and
and ![]() corresponds to the single dot product
corresponds to the single dot product ![]() (82).
(82).
The random, vector, non-diagonal, external interaction for ![]() and
and ![]() is described by the superposition of dot products
is described by the superposition of dot products ![]() (116). So, the random, vector, non-diagonal, internal interaction for
(116). So, the random, vector, non-diagonal, internal interaction for ![]() and
and ![]() is expressed by the single dot product
is expressed by the single dot product ![]() (112) and the random, vector, diagonal, external interaction for
(112) and the random, vector, diagonal, external interaction for ![]() and
and ![]() is represented by the single dot product
is represented by the single dot product ![]() (102), as well. Finally, the random, vector, diagonal, internal interaction for
(102), as well. Finally, the random, vector, diagonal, internal interaction for ![]() and
and ![]() is also reduced to the single dot product
is also reduced to the single dot product ![]() (96).
(96).
Topology of the ck-pulson (201), the dk-pulson (58), the rk-pulson (101), the dg-pulson (56), the rg-pulson (99), the dw-pulsons (53), (55), (135), the rw-pulsons (96), (98), (167), the de-pulsons (133), (134), and the re-pulsons (165), (166) resembles the topology of the solitons on shallow water, the solitary waves on shallow water with uniform and linear vorticity [7] - [8] , the solitary waves generated by crossed electric and magnetic fields [9] , and the pulsatory waves of the Korteweg-de Vries equation [10] .
Topology of the dik-oscillon (72), the drik-oscillon (86), the rik-oscillon (115), the ddk-oscillon (64), the dek-oscillon (77), the drek-oscillon (92), the rek-oscillon (120), the rdk-oscillon (107), the dig-oscillon (71), the drig-oscillon (84), the rig-oscillon (114), the ddg-oscillon (62), the deg-oscillon (75), the dreg-oscillon (89), the reg-oscillon (118), the rdg-oscillon (105), the diw-oscillons (69), (70), (140), the driw-oscillons (82), (83), (189) the riw-oscillons (112), (113), (172), the ddw-oscillons (59), (61), (145), the dew-oscillons (73), (74), (150), the drew-oscillons (87), (88), (196), the rew-oscillons (116), (117), (182), the rdw-oscillons (102), (104), (177), the die-oscillons (138), (139), the drie-oscillons (187), (188), the rie-oscillons (170), (171), the dde-oscillons (143), (144), the dee-oscillons (148), (149), the dree-oscillons (192), (194), the rdee-oscillons (193), (195), the ree-oscillons (180), (181), and the rde-oscillons (175), (176) looks like topology of the nonlinear waves on deep water [11] .
A smooth random function of time as a part of the exact solution of fluid dynamics primarily emerged in the Cauchy integral of motion via a reference pressure p0(t). Theoretical quantization of the kinetic energy of exact wave turbulence includes 8M smooth random functions of time (161)-(162) from C∞ with![]() , which are used to describe random exponential oscillons and pulsons and various interactions between deterministic and random exponential oscillons and pulsons. Construction of smooth random functions of time with oscillatory and pulsatory topologies is an open problem, which will give an opportunity to develop experimental quantization of exact wave turbulence.
, which are used to describe random exponential oscillons and pulsons and various interactions between deterministic and random exponential oscillons and pulsons. Construction of smooth random functions of time with oscillatory and pulsatory topologies is an open problem, which will give an opportunity to develop experimental quantization of exact wave turbulence.
Acknowledgements
The support of CAAM and the University of Mount Saint Vincent is cordially acknowledged. The author thanks a reviewer for helpful comments, which have improved the paper.