Deployment Optimization Strategy for a Two-Tier Wireless Visual Sensor Network ()
1. Introduction
Wireless visual sensor network (VSN) can be considered to be one special type of wireless sensor network (WSN) with visual sensing capability. With development of cheap sensing devices, wireless networking and embedded computer, VSN has become a new technology with tremendous potential for many applications [1]. A VSN typically consists of smart cameras [2], processing chips and wireless transceivers. Besides image capturing function, each smart camera is capable of extracting information from images. Processing chips could do further image processing operations such as image compression or making decisions based on the image data. Wireless transceiver takes care of forwarding image task to the network sink node or the base station (BS). To achieve such a powerful image data handling capability, each visual sensor (VN) is typically equipped with relatively expensive cameras, additional flash memory and more powerful CPU as compared to a conventional wireless sensor. Numerous applications for VSNs have been conceived such as surveillance of public places or remote areas, environments monitoring for animal habitats or hazardous areas, smarthomes for babies and elderly people, and virtual reality [3].
Although a lot of issues in VSN have been studied, there are still many challenges for a VSN [4]. Since VNs are battery-operated device, energy management is one of the important research topics in the VSN community. Among most prior research on VSN, the energy management issue is primarily focused on a single device or a given specific scenario. The notorious energy hole problem [5,6] inherited from WSN research for large scale uniform random distribution VSN has been totally ignored in earlier work. Since wireless sensors need to relay data packets from each other, sensors close to the BS always consume more energy than the sensors located far away. Once close by sensor nodes run out power, the BS gets disconnected from the whole WSN.
Furthermore, the energy hole problem has even worst impact on a large scale VSN than a conventional WSN. While energy consumption in a WSN is dominated only by the data transmission and reception, VSN consumes extra power on image sensing, processing and storage operations. Because of such additional energy consumption, the energy-hole problem of WSNs has a drastic influence on the lifetime of a VSN. In [7], Wang et al. have analyzed the coverage and life time of Gaussian distributed WSN and proposes an optimized deployment strategy that maximizes the lifetime of a WSN. However, since VNs are relatively more expensive than other conventional sensors (e.g., temperature and humidity sensors), deploying more redundant VNs in the inner area following a Gaussian distribution only for energy backup, does not seem to be a cost efficient option. Therefore, Gaussian distribution could not be utilized while deploying VNs.
In this paper, we propose a two-tier deployment strategy for wireless VSN. For a large scale deployment as a uniform random distribution is a cost efficient scheme, especially when there is no previous knowledge about the physical parameters, even though the performance is limited by the energy-hole problem. Therefore, we deploy VNs as a sensing network following a uniform random distribution in a given area, which sense visual data. Since VNs could form a complete WSN, we would like to call it as tier-1 network. In addition to VNs, we propose to deploy another type of sensor nodes called relay nodes (RNs) concentrically distributed parallel to the sensing network. These RNs provides the function of relaying image data to the BS or the sink node.
To take care of the energy hold problem, the relay network deployment basically follows a two-dimensional Gaussian distribution, with mean (μx, μy) at the center of sensing network Although RNs do not generate data, they create acommunication relay infrastructure and we call it as a tier-2 network. Then, the sensing network and the relay network constitute a two-tier wireless VSN, with BS at the center of the monitored region, as illustrated in Figure 1.
Note that as the monitoring tasks and the regions vary, the VSN deployment needs to be designed accordingly. Among many factors, monitored region should be the most important factor to be analyzed. For tier-1 sensing network, an approximated shape of the monitored area is not important since VNs should be distributed in the same symmetrical manner no matter what the shape is. On the contrary, the parameters of the tier-2 relay network standard deviation σ depends on the shape of the region. If the shape of monitored region can be approximated by a circle, square or equilateral triangle, Gaussian distributed relay topology with σx = σy could fit the area very well. If the shape of monitored region is similar to a rectangle or an ellipse, Gaussian distribution with σx ≠ σy could be an appropriate choice for such a scenario. For simplicity, we call two-tier VSN with σx = σy Gaussian distributed relay network as a Circular VSN, and use Elliptical VSN to represent two-tier VSN with σx ≠ σy

Figure 1. Two-tier wireless visual sensor network constructed from Base Station (BS), Visual Sensor Node (VN) and Relay Node (RN).
Gaussian distributed relay network in this paper.
Undoubtedly, for the tier-1 sensing network, the VNs deployment strategy is usually based on the monitoring objective. The monitored area, and the VNs sensing range are preplanned according to special features of the VSN project and the only question needed to be answered is:
• How many VNs should be deployed for the monitored region to satisfy the coverage requirement?
For tier-2 relay network, there are two key questions that need to be addressed before deployment:
• How many RNs should be deployed within the tier-1 sensing network?
• How to configure the parameters of the Gaussian distributed RNs so as to optimize the performance?
To answer these questions, theoretical analysis and modeling for two-tier VSN is needed. We choose lifetime and cost as our objectives to measure the performance of VSN under different deployment strategies. Analysis on coverage and connectivity of two-tier VSN is necessary right at the beginning. Thereafter, the optimization problem can be defined in terms of lifetime and cost of the VSN so as to reflect the optimized deployment parameters. The main contributions of our work here are as follows:
• We present an analytical model for the coverage and the connectivity of a Circular VSN and establish a relationship between the network requirements and VSN deployment parameters from the geometry point of view.
• We provide a new formalism to model an Elliptical VSN and derive an analytical model.
• With the analytical model, we propose two global optimal search algorithms for Circular VSN and Elliptical VSN to obtain optimal deployment parameters.
• Based on the shape of the monitored region, we suggest a large scale VSN should be divided into several small VSNs for monitoring different types of tasks.
The rest of the paper is organized as follows. Related works are discussed in Section 2. The system model is introduced in Section 3. In Section 4, we analyze the coverage and connectivity of Circular VSN. The coverage and connectivity of Elliptical VSN are discussed in Section 5. Then, in Section 6, we propose deployment strategies for a large scale VSN with optimization in mind. Finally, Section 6 concludes the paper.
2. Related Works
WSN related topics have been extensively studied in recent years, and many researchers have provided substantial theoretical and practical results. Some theories and algorithms for WSN could be directly applied to VSN. However, many challenging issues are still open for VSN. In this section, we would like to review energy management schemes for VSN and lifetime optimization strategies for WSN.
2.1. Energy Management of Wireless Visual Sensor Network
Charfi et al. [4] discussed several research issues on the optimization of smart camera coverage, low-power image processing, VSN architecture, and wireless communication. Since a wireless sensor in a VSN is a batterydriven device, energy management is always an important research topic. Due to severe energy constraints on VSN, many works have been done on how to use the energy efficiently. Coordinated Distributed Power Management (CDPM) policy for VSN has been proposed by Zamora and Marculescu in [8]. Their CDPM policies include dynamic and adaptive timeout thresholds, hybrid CDPM, two-hop broadcast information dissemination, and remote wakeup.
Soro and Heinzelman [9] presented two camera selection schemes in providing longer lifetime in a network. One scheme selects cameras that minimize the difference between captured images and the other scheme is based on choosing a VN by considering the energy constraints and the three-dimensional coverage. Since the data transmitted in a VSN are images captured by smart cameras and the amount of data has a huge impact on the energy consumed by data forwarding operation, image compression technique is one of the solutions for efficient energy management of a VSN.
Dagher in [10] analyzed the interand intra-sensor correlation for power-constrained VSN and proposed an algorithm using a compression scheme. Margi et al. [11] conducted an energy consumption experiment on a visual sensor testbed to determine the power utilization for different image handling tasks. The results of their experiments provide a comprehensive understanding of energy consumption in a VSN.
Hadi et al. [12] proposed a two-tier topology for camera-based wireless multimedia sensor networks. A number of Non-camera sensor nodes with powerful CPU processing ability are deployed above the lower-tier visual sensor network to form a higher-tier network. To combine multiple images from lower-tier visual sensor nodes, higher-tier sensor nodes perform Image stitching to create a high-resolution image. Energy consumption is minimized by reducing the redundant data being forwarded for the overlapping areas covering multiple images.
To summarize, most prior VSN energy management research focused only on a single visual sensor node or a given specific scenario. To our knowledge, energy-hole issue has not been considered for a large scale VSN. Thus, our study focuses on solving energy-hole problem while increasing the lifetime of VSN with minimal cost.
2.2. Lifetime Optimization of Wireless Sensor Network
Many theoretical results about coverage, connectivity and lifetime have been proposed for randomly distributed large scale WSN. Uniform randomly distributed WSN has attracted more attention from researchers, since from a practical point of view; it is a good option for different sensing tasks, especially when there is no previous knowledge about the deployed area. But, the drawback of uniform random distribution WSN is a well-known energyhole problem for periodic data collection applications. Li et al. [13] show that lifetime of a uniformly distributed WSN is limited by the sensor nodes one-hop away from the BS and they also suggest several schemes to minimize the impact of energy-hole problem.
In order to increase the data capacity of WSN, a nonuniform distribution strategy has been proposed by Lian et al. in [14]. The results show that up to 90% of initial network energy is wasted when WSN becomes disconnected, when the sensor nodes close to the BS runs out of energy. Some controllable random distribution schemes are proposed to address the energy-hole problem. A strategy is provided by Wu et al. [15] to balance the energy depletion of a WSN. They propose to deploy sensors from outer area to inner area according to certain geometric proportion. Liu et al. [16] proposed a nonuniform deployment scheme for enhancing the lifetime of WSN. The results in [16] shows that the scheme can mostly take care of the energy-hole problem.
However, all these strategies are under the assumption that the location of sensors in the deployed region can be accurately controlled, which is impractical for some real applications. Zou et al. [17] proposed an idea that sensors could be distributed following two-dimensional Gaussian distribution without detailed analysis. Afterwards, Wang et al. [7] provided a comprehensive analysis on the coverage and the lifetime of a two-dimensional Gaussian distributed WSN and optimization algorithms are provided to find the optimal deployment parameters that increase the lifetime of WSN so as to relax the impact of the energy-hole problem.
Although all existing schemes provided desirable results for WSNs, we feel that they cannot be directly applied to VSN deployment. The essences of these schemes are based on adding more sensors closer to the BS to handle data forwarding tasks. These ideas fit well in a WSN environment, especially when the sensor hardware cost keeps going down, benefiting from the advances in the sensor industry. But, VNs in VSN are relatively expensive sensors with smart cameras. Simply deploying more VNs for energy backup will definitely increase the cost and is not an acceptable option for an optimal design of a monitoring task. Therefore, we propose two-tier VSN strategy to simultaneously relax the energy-hole and cost wastage problems.
In the following section we will describe the network sensor system model by first describing the Network deployment model, the energy model and then the sensing and connectivity model.
3. Sensor System Models
In this section, we introduce models for the network deployment, sensor energy, sensing and connectivity for wireless VSNs.
3.1. Network Deployment Models
1) Random Distribution Sensing Network: Consider that a large number of M VNs need to be deployed in a twodimensional geographical region D, and the BS is located at the center, forming our tier-1 sensing network. We assume that the VNs are deployed uniformly and independently, and we could call it as uniform VSN for short.
When prior knowledge of the region is not available, such a random deployment could be an effective method. Under this scenario, location of VNs could be modeled as a stationary 2-D Poisson point process [18]. Denote the number of visual sensors in field D as N (D), which follows the Poisson distribution as:
 (1)
(1)
where λ is density of the Poisson point process and  is the area of region D. An example of a two-dimensional randomly distributed sensor network is shown in Figure 2 with BS at the center.
is the area of region D. An example of a two-dimensional randomly distributed sensor network is shown in Figure 2 with BS at the center.
2) Gaussian Distribution Relay Network: We consider that a network with N relay nodes are deployed in a twodimensional plane, which is called tier-2 or relay network in this paper. The RNs deployment pattern follows twodimensional Gaussian distribution as:
 (2)
(2)
where (xi, yi) is the position of the BS and σx and σy are the standard deviation for x and y directions. To simplify the analysis, let the sink node position be xi = 0, yi = 0, then we have:
 (3)
(3)
A two-dimensional Gaussian distribution with σx = σy relay network example is shown in Figure 3 with BS at the center.
3.2. Energy Models
1) Relay Node Energy Models: Since RNs do not generate any data, energy consumption is dominated only by the radio communication system (i.e., data transmission and reception tasks). When RNs relay image data, we can determine the energy consumption using the first order radio model described in [19]. The energy Et(m, d) consumed by transmitting m-bit packet to distance d can be given by:

Figure 2. Two-dimensional randomly distributed sensing network with Base Station (BS) and Visual Sensor Node (VN).

Figure 3. Two-dimensional gaussian randomly distributed relay network with Base Station (BS) and Relay Node (RN).
 (4)
(4)
where Eelec is the energy cost to activate the transmitter or receiver circuit and  is for the communication transmitter amplifier. During reception by a RN, energy consumption only depends on the data load. So, total energy consumed Er (m) can be given by:
is for the communication transmitter amplifier. During reception by a RN, energy consumption only depends on the data load. So, total energy consumed Er (m) can be given by:
 (5)
(5)
where Eelec is the same as Equation (4). Suppose VNs collect L' bits of image data in each sampling cycle, and the image data must be divided into several small m bits data packets to be communicated from VNs to the BS. With additional header overhead bits, let us use notation L, where L > L', for total bits of packets in every data collection cycle generated by each VN. When the transmission distance d is set as the sensor radio transmission range rc, the total transmission energy used for each sampling cycle can be computed by:
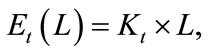 (6)
(6)
where , and we can calculate the reception energy Er (L) as
, and we can calculate the reception energy Er (L) as
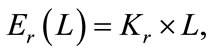 (7)
(7)
where . Although RNs and VNs have different functions, their radio system certainly can be the same hardware as RNs. Thus, Equations (6) and (7) can also be used for VNs communication energy calculation.
. Although RNs and VNs have different functions, their radio system certainly can be the same hardware as RNs. Thus, Equations (6) and (7) can also be used for VNs communication energy calculation.
2) Visual Sensor Energy Models: Typically, WSN include relatively simple sensors, such as temperature, humidity and light sensors, etc., and energy consumption is dominated by the wireless transmission and reception of WSN radio communication system. However, due to the significant difference in sensing hardware (i.e., cameras) of VSN, the common energy consumption model in WSN apparently cannot be utilized for VSN energy calculation. The energy measurement experiment for VN in [11] provides us a comprehensive understanding of energy consumption during visual sensor running session. Margi et al. [11] conducted measurements on their Meerkats testbed (Crossbow’s Stargates, Orinoco Gold 802.11b PCMCIA wireless card and Logitech QuickCam Pro4000 webcam). The main energy consumption tasks of VN in one sampling operation cycle includes:
• Sensing Energy Ee: Energy consumed for collecting image data by a camera
• Storage Energy Es: Energy used for writing and reading image data on a flash memory.
• Processing Energy Ep: Energy consumed in performing Fourier Transform for images.
• Transmission Energy Et: Energy in sending image data to the neighboring nodes.
• Reception Energy Er: Energy consumed for reception of neighboring wireless nodes.
The transmission energy Et(L) and reception energy Et(L) are already considered in the RNs energy model. So, we focus on other aspects of the energy model. The sensing, storage and processing energy models would vary for different sensor hardware and an accurate energy consumption model is beyond the scope of this paper. But, based on the observation of the experiments data [11] and the nature of circuit, we use the first order energy model to estimate the energy consumption for sensing, storage and processing tasks as:
 (8)
(8)
 (9)
(9)
 (10)
(10)
3.3. Sensing and Connectivity Models
1) Network Sensing Range Model: For research in WSN, a circular shaped coverage by a sensor is always assumed. On the contrary, smart cameras on VNs normally cover less than 180˚ area. However, since smart cameras shooting angle can be remotely adjusted to a proper direction by the network operator, we still use a circular shape to estimate the coverage of our proposed two-tier network. VNs are randomly and independently deployed in a two-dimensional region. Liu et al. [18] show that for such a randomly deployed sensor network in a two-dimensional infinite plane, the probability fa that a point is covered by at least one sensor is as follows:
 (11)
(11)
where λ is the node density and rs is sensing range of each sensor node. Sensing task is performed only by VNs. Thus, Equation (11) can be utilized for our random distribution tier-1 sensing network directly and minimal number of VNs for a given region can be estimated.
2) Network Transmission Range Model: In a random uniform distribution network, Bettstetter in [20] showed a relationship between the sensor transmission range rc and the network connectivity as:
 (12)
(12)
where p is the possibility that none of the sensor node in the network is isolated, n is the total number of sensor nodes deployed in the large area A satisfying , and
, and  is the node density. Equation (12) is only for random uniform distribution, while, this can be still useful in our Gaussian distribution relay network analysis of Section 4.
is the node density. Equation (12) is only for random uniform distribution, while, this can be still useful in our Gaussian distribution relay network analysis of Section 4.
4. Coverage and Connectivity of Circular Wireless Visual Sensor Network
In this section, we present an analysis for Circular VSN to satisfy the basic network requirement of both the coverage and the connectivity. We consider a two-tier wireless visual sensor network: tier-1 sensing network with random uniform distribution consists of VN with a sensing range rs and transmission range of rc; tier-2 relay network with random Gaussian distribution consists of RNs with the same transmission range rc. In this section, we analyze Circular VSN by modifying Equation (3) as:
 (13)
(13)
Two networks are concentric and have the same BS at the center point. Figure 4 shows an example of our deployment strategy in a two-dimension plane with sink node (star) at the center, VNs as green triangles and RNs as blue dots. Next, we discuss a scheme of deploying the VNs and RNs to guarantee the coverage of the area and their connectivity to the BS.
4.1. Coverage of Circular VSN
Apparently, sensing function of a two-tier network is done only by the sensing network at tier-1. Coverage of two-tier network depends on uniformly distributed sensing network and coverage probability Ps can be given based on Equation (11) as:
 (14)
(14)
where M is the number of VNs and A is the area of monitored region. rs depends on the sensing capability of

Figure 4. An example of Circular VSN in monitored region with Base Station (BS), Visual Sensor Node (VN) and Relay Node (RN).
camera on VNs. Once rs is set based on visual task, coverage probability would increase when more VNs are deployed in a given area.
Assume the coverage requirement as  (e.g., 95%). To guarantee the coverage of tier-1 network, we need at least M VNs satisfying:
(e.g., 95%). To guarantee the coverage of tier-1 network, we need at least M VNs satisfying:
 (15)
(15)
Equation (15) provides a theory to support optimized cost for wireless VSN, while meeting the coverage requirement at the same time.
4.2. Connectivity of Circular VSN
VNs and RNs have the same radio hardware and transmission range rc and two sensors can communicate with each other if they are within each other’s distance rc which is a preplanned parameter. If rc is set too small, either the network connectivity is compromised or additional sensors ought to be deployed, adding to the cost. But, due to hardware limitations, rc cannot be adjusted arbitrarily and there is a maximal radio transmission range 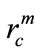 limiting
limiting . rc should be set to be a proper max value as long as wireless link quality could meet the requirements.
. rc should be set to be a proper max value as long as wireless link quality could meet the requirements.
To analyze a Circular VSN, two-tier network is modeled as a disk as is done in [7]. The disk with radius R is divided to multiple annuli as shown in Figure 5, and the center of disk is at the origin of XY plane, where sink node is located. The width of annuli is rc, which is the transmission range of VNs and RNs. Annuli is marked

Figure 5. Disk annuli division of a Circular VSN.
from 1 to k where . Then, any sensor node with distance d to the BS always falls inside ith annuli of disk if d satisfies
. Then, any sensor node with distance d to the BS always falls inside ith annuli of disk if d satisfies . To consider tier-1 network only, sensing network is divided into [1, 2, ∙∙∙, k] annuli and since tier-1 network follows a uniform random distribution, VNs node density
. To consider tier-1 network only, sensing network is divided into [1, 2, ∙∙∙, k] annuli and since tier-1 network follows a uniform random distribution, VNs node density  is the same in each annulus. Relay network is planned to be deployed concentrically to the sensing network and since the relay network follows a Gaussian distribution, inner annuli RNs node density
is the same in each annulus. Relay network is planned to be deployed concentrically to the sensing network and since the relay network follows a Gaussian distribution, inner annuli RNs node density  is larger than outer annuli node density.
is larger than outer annuli node density.
We assume VNs only sense visual data and send packets to neighbouring RNs and VNs do not relay any packets. Rest of the packets forwarding need to be handled only by the relay network. Furthermore, all traffic from outer annulus i + 1 is distributed uniformly among the RNs in annulus i. This assumption requires an ideal routing mechanism in such a way that the traffic load from VNs is uniformly allocated to RNs in the same annulus and relaying traffic load is also allocated uniformly to RNs in one-hop annulus, which would balance the residual energy for all the RNs. Although Equation (12) is proposed for a uniform random distribution, we apply this model to calculate the network connectivity in each annulus after an appropriate annuli division of the whole region. Since annulus width , distribution of RNs inside each annulus is approximated as a uniform distribution.
, distribution of RNs inside each annulus is approximated as a uniform distribution.
To guarantee the connectivity inside each annulus, we utilize Equation (12) with the scenario that each VN only send packets to RNs located in the same annulus. Then, if VNs send packets to one-hop annulus RNs, fewer RNs in the same annulus is needed and the network connectivity is still guaranteed. Network connectivity is a crucial requirement and worth more discussion. For each VN, connectivity of a two-tier network actually means connectivity of a large number of uniform random distributed RNs. Rewriting Equation (12) for annulus i as:
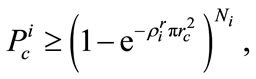 (16)
(16)
where Ni is the number of RNs in the annulus i and  is i annulus node density of RNs. When deployed target region and RNs radio transmission range rc are given, Equation (16) indicates the relation between the connectivity probability and the number of deployed sensors.
is i annulus node density of RNs. When deployed target region and RNs radio transmission range rc are given, Equation (16) indicates the relation between the connectivity probability and the number of deployed sensors.
If the network connectivity requirement is satisfied in the outermost annulus k with Nk relay nodes, then the relay network can guarantee connectivity of the network, as all inner annuli of Gaussian distributed relay network have a higher node density than the outermost annulus. Assuming the network connectivity requirement is 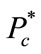 and outermost annulus k connectivity is
and outermost annulus k connectivity is , then we need at least
, then we need at least 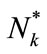 relay nodes in annulus k satisfying:
relay nodes in annulus k satisfying:
 (17)
(17)
With disk annuli modeling, we have a relation between Nk and the total number N as:
 (18)
(18)
where Pi is the probability that a RN is in the ith annulus of VSN network and can be calculated by:
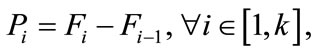 (19)
(19)
where Fi indicates cumulative distribution function (CDF) of two-dimension Gaussian distribution over a circular area, whose radius is irc. If we plot the 2D Gaussian distribution f(x, y) as Z axis direction in a three-dimension space X, Y, Z, itis clear that Fi is the volume enclosed by XY plane and Gaussian distribution function f(x, y). As in Figure 6, the mesh represent probability distribution of RNs among X, Y plane, and the volume of purple solid “ring” object is the cumulative probability of RNs with annulus i. Thus, Pi can be calculated by the volume of the “purple ring” enclosed by annulus i area on XY plane and Gaussian function f(x, y). f(x, y) is probability distribution function, so it is always positive. And since f(x, y) = f(–x, y) = f(x, –y) = f(–x, –y), f(x, y) is symmetric to X, Y axis. The whole volume enclosed by f(x, y) boundary is four times of the volume in the first octant (X+, Y+, Z+). Then, we can compute Fi based on the rules in calculus application in geometry as:
 (20)
(20)
With the help of polar coordinates transformation, we have:
 (21)
(21)

Figure 6. Ring interpretation of Pi in a 3D space.
From Equations (19) and (21), we have:
 (22)
(22)
Based on Equations (17)-(22), we establish a relation between total number of RNs and the connectivity requirement as:
 (23)
(23)
where  and Ak is the area of annulus k.
and Ak is the area of annulus k.
5. Coverage and Connectivity of Elliptical Wireless Visual Sensor Network
In this section, the coverage and the connectivity of Elliptical VSN is discussed. One example is shown in Figure 7 as an ellipse-shape two-tier VSN.
5.1. Coverage of Elliptical VSN
Similar Circular VSN, coverage of two-tier Elliptical VSN only depends on tier-1 sensing network. Thus, Equation (14) can be used for computing the coverage probability of Elliptical VSN. Also, if we have the coverage probability requirement , we can utilize Equation (15) to calculate required minimal number of VNs in the sensing network.
, we can utilize Equation (15) to calculate required minimal number of VNs in the sensing network.
5.2. Connectivity of Elliptical VSN
Different from a Circular VSN, tier-2 relay network deployment of Elliptical VSN follows two-dimensional Gaussian distribution following Equation (3) with a mean of (xi, yi) at the center of monitored region and standard variations (σx ≠ σy). To analyze an Elliptical VSN, it could be modeled as an ellipse shape:
 (24)
(24)
where a and b are half of the ellipse’s major and minor axes respectively. Then, similar to the disk annuli formalism in Section 4, we can divide the whole area into multiple annuli as shown in Figure 8. The center of ellipse is at the origin of XY plane, where the BS is located. To guarantee the connectivity of VSN, we designed ellipse division as follows. Without losing generality, we assume a > b for the whole VSN. We divide a on the positive X axis first into multiple line segments with width of rc, then we have  line segment on
line segment on

Figure 7. An example of Elliptical VSN in monitored region with Base Station (BS), Visual Sensor Node (VN) and Relay Node (RN).

Figure 8. Ellipse annuli division of Elliptical VSN.
positive X axis. Second, minor axes of VSN on positive Y axis is cut into k line segment with width . Finally, irc and irb, where
. Finally, irc and irb, where , are used as half of the major and minor axes of ellipse to build ellipses in XY plane. Now, we have a multiple elliptical annuli VSN. Since
, are used as half of the major and minor axes of ellipse to build ellipses in XY plane. Now, we have a multiple elliptical annuli VSN. Since , any node in annulus i could transmit packets to one-hop annulus towards the BS. Similar to the disk division, tier-1 network is divided into
, any node in annulus i could transmit packets to one-hop annulus towards the BS. Similar to the disk division, tier-1 network is divided into  annuli and VNs node density
annuli and VNs node density 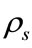 is the same in each annulus. Tier-2 network’s inner annuli RNs node density
is the same in each annulus. Tier-2 network’s inner annuli RNs node density  is larger than the outer annuli node density, but within each annulus, RNs node density
is larger than the outer annuli node density, but within each annulus, RNs node density  is the same as long as
is the same as long as .
.
Assuming the network connectivity requirement is  and we need at least Nk relay nodes in the annulus k satisfying Equation (17). Similar to the disk division modeling, Fi can be calculated by integrating as:
and we need at least Nk relay nodes in the annulus k satisfying Equation (17). Similar to the disk division modeling, Fi can be calculated by integrating as:
 (25)
(25)
With ellipse polar coordinates:
 (26)
(26)
we can transform Equation (2) to:
 (27)
(27)
Finally, we can obtain Fi using:
 (28)
(28)
where . Equation (28) can be solved with a numerical integral method by following an adaptive recursive Simpson’s rule. Based on Equations (19) and (28), we have:
. Equation (28) can be solved with a numerical integral method by following an adaptive recursive Simpson’s rule. Based on Equations (19) and (28), we have:
 (29)
(29)
With Equations (28) and (29), we obtain a relation between the number of RNs N and connectivity requirements  as:
as:
 (30)
(30)
6. Deployment Optimization of Large Scale Wireless Visual Sensor Network
In Section 4 and Section 5, we analyzed the coverage and connectivity requirement of at least M VNs in a uniformly distributed tier-1 sensing network and Nk RNs in annulus k of Gaussian distributed tier-2 relay network. For tier-2 relay network, choosing N and σ of Gaussian distribution in a cost efficient manner is challenging. If we choose σ as a relative small value, then we need additional RNs to satisfy the connectivity requirement, which would add to the cost. On the other hand, for certain number N RNs, if we choose a too large σ, the lifetime of network is reduced because of the energy-hole problem in the center area, and the cost of RNs and VNs in the outer area simply become useless. Therefore, in this section, we proposed optimal deployment strategies in term of the lifetime and the cost for both Circular VSN and Elliptical VSN satisfying the coverage and the connectivity constraints.
6.1. Optimal Deployment Strategy for Circular VSN
Suppose we have M VNs and N RNs in a two-tier network deployed in the monitored region and divided into multiple annuluses. Each wireless node has the same initial energy level E0. The traffic pattern we considered implies that each visual sensor periodically senses image data and send to sink node located at the center of the network. Data collection interval of sensing network is denoted by . In each data collection cycle, each VN generates L bits image data and RNs have the responsibility to forward them image to the sink node. We neglect the energy consumed by other network in the communication procedure, such as routing, MAC collisions, and assisting information exchange.
. In each data collection cycle, each VN generates L bits image data and RNs have the responsibility to forward them image to the sink node. We neglect the energy consumed by other network in the communication procedure, such as routing, MAC collisions, and assisting information exchange.
We use the notation  to indicate the lifetime of ith annulus VNs and since all VNs follow the same data collection procedure (i.e., sensing, storing, processing and transmitting) in each cycle, VNs will deplete their energy at the same time. Based on the energy model of section 3, VNs lifetime can be estimated by:
to indicate the lifetime of ith annulus VNs and since all VNs follow the same data collection procedure (i.e., sensing, storing, processing and transmitting) in each cycle, VNs will deplete their energy at the same time. Based on the energy model of section 3, VNs lifetime can be estimated by:
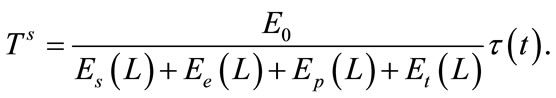 (31)
(31)
For analyzing tier-2 relay network, an energy balanced ideal routing scheme is assumed, which allocates traffic load equally to RNs. Thus, energy consumption rate for all RNs in each annulus are the same. Since RNs do not generate any data, the traffic load RNs received is equal to traffic load they transmit. We assume all the traffic load in annulus i from VNs are allocated on the same annulus RNs. So, a larger number of relatively cheaper RNs are needed. However, lifetime of VNs is not limited by the lifetime of the relay network. The traffic load in annulus i for all RNs, denoted by Loadi can be calculated as:
 (32)
(32)
where Ai is area of annulus i and can be computed easily with , and
, and  is the node density of VNs and can be calculated by
is the node density of VNs and can be calculated by . Since one-hop away VNs can directly send image data to BS, workload of RNs in annulus 1 and 2 are the same, i.e., Load1 = Load2. Then, the total energy consumed in one data collection cycle can be expressed as:
. Since one-hop away VNs can directly send image data to BS, workload of RNs in annulus 1 and 2 are the same, i.e., Load1 = Load2. Then, the total energy consumed in one data collection cycle can be expressed as:
 (33)
(33)
We have Ni out of N RNs deployed in annulus i expressed as in Equation (18). Let  be the lifetime of RNs in i annulus and can be estimated as in [7] with Equations (32) and (33):
be the lifetime of RNs in i annulus and can be estimated as in [7] with Equations (32) and (33):
 (34)
(34)
Lifetime T of two-tier network is defined as the time period when the battery-driven sensing network and the relay network are running simultaneously in all [1, k] annuli. In other words, if any annulus VNs or RNs runs out of initial power E0, lifetime of the network ends. If Ti denotes lifetime of annulus i network, our VSN lifetime T is calculated by:
 (35)
(35)
We use the notation Cr and Cs for the cost of each RN and VN, respectively. Then, the total cost of sensor devices denoted by C can be computed as:
 (36)
(36)
With the knowledge of coverage and connectivity requirements  and
and , our deployment optimization can be modeled by the following objective and constraints:
, our deployment optimization can be modeled by the following objective and constraints:
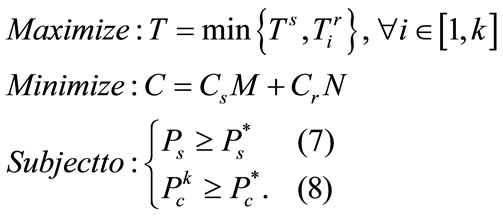 (37)
(37)
Coverage and connectivity constraints are shown by Equations (15) and (17). The multi-objective optimization problem modeled in Equation (37) typically can be translated into a single objective optimization after normalization as:
 (38)
(38)
where α, β are the weights of the corresponding two objectives, representing which objective is more important for deployment of VSN. Logarithm function is used to normalize two objectives and reduce the impact of individual attribute scale. For example, if the cost C is a large number and T is a small one, then without logarithm function, our objective will be dominated by the cost only. With logarithm function, we have
 (39)
(39)
and two objectives T and C are normalized. Now, we can maximize W satisfying two constraints. Lifetime and cost are always the most important concern for any WSN project. It is easy to increase the lifetime of sensors by increasing the cost, namely deploying a lot more additional battery-driven sensors. But, maximizing the lifetime with minimal cost is always preferred for any project. Therefore, strategy with a reasonable tradeoff between the lifetime and the cost is desirable.
The single-objective optimization problem expressed by Equation (38) can be solved by brute-force search algorithms. To reduce the search spaces (i.e., range of N, M and σ), prior knowledge of VSN deployment can be used to narrow possible combinations. At first, coverage probability is a non-decreasing monotone function and only depends on the number of VNs M. Then, increasing from a small M, the first M satisfying coverage requirement is the minimal M for tier-1 sensing network. For tier-2 relay network, deployment parameters N is integer; and σ can be approximated by an integer close-to-optimal result and is enough for deployment in a large region.
A search for the range on the number of RNs N has an upper bound for a given deployment budget cost. But, since W is a non-linear function and some local optimal maximum might exist, the range of σ would be chosen carefully. Narrow range of search would not return in an optimal objective and wide range would dramatically increase the algorithm computing complexity.
For a Circular VSN deployment, monitored region normally has a limited boundary and RNs or VNs could be deployed by a low-flying helicopter or a UAV from the sky or can be projected by artillery. Although very small value of σ can causemore cost, lower bound of σ can be simply set as 1, since very small value of σ is automatically restricted by Nmax and connectivity requirements. For upper bound of σ, since the deployment of randomly distributed RNs can not be fully controllable and position of RNs can not be predicted accurately, a large value of σ means more RNs are likely to fall outside of monitored area, which caused additional waste. Therefore, we can attain the maximal σ through the analysis of what percent of RNs fall within monitored area with CDF Fi in Equation (21).
For example, for Circular VSN in a R = 500 m cycle region, we have a relation between CDF Fk and σ as shown in Figure 9. If we have a threshold 90%, which means we allow that 10% RNs can be out of the monitored area during random deployment in a large area, we can have range of σ is [1, 234]. The threshold for obtaining σmax varies for different VSN and depends on many factors such as the cost budget, detailed situations in the monitored region etc. Then, we can use this method to find search space of σ for different regions. With search space [1, Mmax], [1, Nmax], and [1, σmax], we present pseudo code of a brute-force search optimal procedure inAlgorithm 1" target="_self"> Algorithm 1. The computational complexity is analyzed by Lemma 1.
Lemma 1.Algorithm 1" target="_self"> Algorithm 1 has a polynomial time computational complexity.
Proof.Algorithm 1" target="_self"> Algorithm 1 uses a brute-force search method to find a global optimal result for circular VSN, and searching of optimal sensing network parameter Mopt while optimal relay network parameters σ, N are separated. Searching space for three parameters M, N, σ are [1, Mmax], [1, Nmax], and [1, σmax], respectively.
Searching for an optimal number of VNs Mopt in sensing network would use one FOR loop and the cost with O(Mmax) computing complexity. In searching for optimal parameters in a relay network, one k computing steps loop is used to calculate lifetime of individual k annulus of VSN for all combination of N and σ. Assuming calculation of lifetime complexity is O(L) and extra complexity for network cost is O(C), then we need O(k × L + C) for different N and σ. Complexity for searching relay network parameter would be O (Mmax × σmax × (k × L + C)). So, the net complexity ofAlgorithm 1" target="_self"> Algorithm 1 is O(Mmax × σmax × (k × L + C) + Mmax), which is a polynomialtime
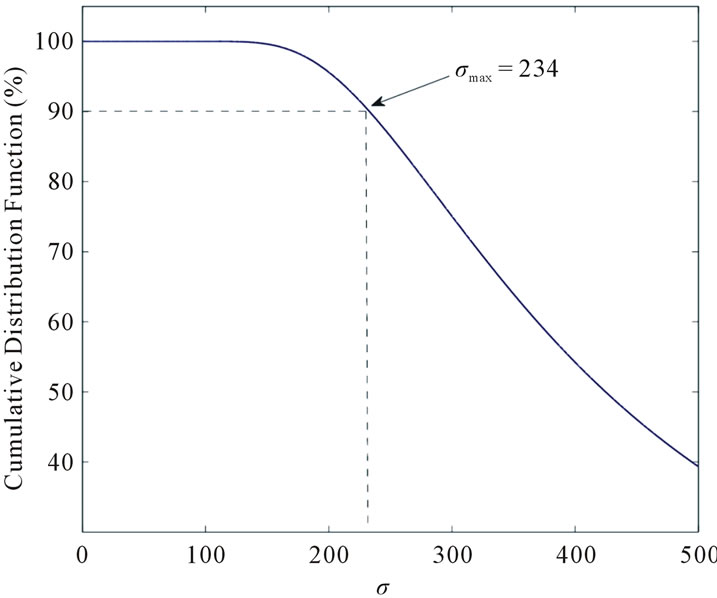
Figure 9. Analysis of maximal value of σ.


Algorithm 1. Global optimal parameters search algorithm for a Circular VSN.
complexity. Based on a priori knowledge of the VSN, Mmax < Nmax. Computing cost needs fewer steps than computing the lifetime, which needs constant steps. Finally,Algorithm 1" target="_self"> Algorithm 1 computing complexity could be represented as O(Mmax × σmax × k) for different size of the region and the search method clearly has a polynomial time computational complexity.
With Algorithm 1, the performance of proposed deployment strategy is investigated for the regions with different radius R. We compare our proposed deployment strategy results with two common deployment strategies: uniform random distribution and Gaussian distribution strategy. Sink node is always assumed to be at the center of deployed region. The VSN parameters in analysis are shown in Table 1. Weights α, β stands for weights for the lifetime and the cost object, and we always treat two

Table 1. Parameters for a wireless visual sensor network.
objectives equally in our evaluation.
To guarantee fairness in comparing the performance, we conduct our analysis in the following manner: for different regions with radius R, we calculate the optimal number of VNs M, number of RNs N and tier-2 Gaussian distribution deviation σ for our proposed deployment strategy. Next, cost C and lifetime T of VSN are evaluated for our proposed strategy. For comparison purpose, we first utilize the same cost amount to uniformly random VSN and Gaussian distributed VSN and then compare lifetime for three strategies under the same budget. Next, we compare the cost of the uniform and Gaussian distribution to our proposed deployment scheme when the lifetime of the network is maintained at certain period. For uniform random distributed VSN, VNs are uniformly and independently deployed in the monitored region and are responsible for data collection and forwarding. For conventional one-tier Gaussian distributed VSN, VNs are deployed as Gaussian distribution and they would take care of both data collection and forwarding. In the evaluation, we would search optimal Gaussian parameters to guarantee the performance of one-tier Gaussian distribution strategy. We compare three strategies for Circular VSN with radius R = 500 m, 800 m, 1000 m, 1500 m respectively.
Figure 10 shows the lifetime of VSN in different monitored region using three strategies. We first implement our proposed scheme to optimize deployment parameters for a two-tier VSN. Then, we compute the total cost of our deployment cost C for four regions and invest the same cost to deploy VNs with two other existing strategies into the same region. From Figure 10, due to energy-hole problem and cost budget, we can clearly see that in all three strategies, VSN lifetime decreases as area of monitored region increases, which verifies the correctness of our analytical method.
Figure 10 also shows that, as compared to existing strategies, our proposed scheme always has the best lifetime performance with the same cost for a given area. Using R = 500 m as an example, our proposed two-tier strategy can achieve 1250 hours VSN lifetime with cost $8975. But, uniform strategy VSN can only last 89 hours and conventional Gaussian VSN can reach to 200 hours with the same cost investment. For limited budget, our proposed two-tier VSN has 190 hours lifetime in a largearea R = 1500 m, but still beats 14 hours for uniform VSN and 37 hours for conventional Gaussian VSN.
To verify the usefulness of our proposed strategy in cost saving aspect, we also calculate the cost of three strategies when the lifetime of VSN must be maintained as certain hours. We calculate the cost of four different regions with radius R = 500 m, 800 m, 1000 m, 1500 m, respectively. Based on the results of lifetime analysis above, we compare three schemes cost when the lifetime is maintained as 1250 hours, 1249 hours, 605 hours, and 190 hours for four different regions.
As shown in Figure 11, the total budget of our proposed two-tier VSN is $8975, $35,720, $50,000 and $100,000 for four different regions. The cost of uniform VSN is $125,680, $610,520, $769,440 and $1,327,800, respectively. Cost of a uniform VSN increase dramatically when the region area get larger. One-tier Gaussian strategy costs $22,040, $107,480, $144,680 and $275,620 for four analyzed regions. Its performance on cost aspect is better than a uniform VSN, which is already shown in

Figure 10. Lifetime comparison of three strategies with the same cost for Circular VSN.

Figure 11. Cost comparison of two strategies with different region radius for Circular VSN.
many previous related work, but still worse than our proposed two-tier strategy. The analysis illustrates that no matter what the objective is, lifetime or cost, our proposed two-tier VSN deployment optimization strategy is observed to provide a better performance than a commonly distributed deployment strategy.
6.2. Optimal deployment Strategy for Elliptical VSN
Suppose we have a two-tier Elliptical VSN with M VNs and N RNs, which is divided into multiple annuli. Similar to Circular VSN, we can model the deployment strategy optimization problem as Equation (38). But, the difference is that we need to search for four deployment parameters M, N, σx, and σy, since σx ≠ σy. Although more parameters need to be optimized, brute-force search algorithm still works for Elliptical VSN. Search algorithm described in Algorithm 1 is presented for Elliptical VSN deployment strategy optimization.
Similar to a Circular VSN, the search space could be decided. Mmax and Nmax could be fixed based on the cost budget. Large values of  and
and  might cause unnecessary additional cost, since RNs might be deployed outside the monitored region. Thus,
might cause unnecessary additional cost, since RNs might be deployed outside the monitored region. Thus,  and
and  could be obtained in the way similar to Circular VSN scenario. Figure 12 shows us the relation between σx and σy and CDF when an Elliptical VSN is modeled as an ellipse with major axes is 1000 m and minor axes is 800 m. CDF at Z axis indicates the percent of RNs within the monitored area. For example, when σx = 600 and σy = 400, there are around 75% RNs are within region boundary and about 25% are wasted, then we can set
could be obtained in the way similar to Circular VSN scenario. Figure 12 shows us the relation between σx and σy and CDF when an Elliptical VSN is modeled as an ellipse with major axes is 1000 m and minor axes is 800 m. CDF at Z axis indicates the percent of RNs within the monitored area. For example, when σx = 600 and σy = 400, there are around 75% RNs are within region boundary and about 25% are wasted, then we can set  = 600 and
= 600 and  if the threshold of 75% is accept-
if the threshold of 75% is accept-

Figure 12. Analysis of maximal range of σx, σy.
able for monitored task. Now, we have the search space for Elliptical VSN optimization. Algorithm 2 is presented for optimization procedure, and computational complexity is discussed in Lemma 2.
Lemma 2. Algorithm 2 has a polynomial time computational complexity.
Proof. Same asAlgorithm 1" target="_self"> Algorithm 1, Algorithm 2 also use brute-force search method to find global optimal results for circular VSN, but searching need to be done for four parameters since σx ≠ σy. Searching space for four parameters M, N, σx, σy are [1, Mmax], [1, Nmax], [1, ], and [1,
], and [1, ] respectively.
] respectively.
Searching of optimal number of VNs Mopt in sensing network still cost O(Mmax) computing complexity. In searching optimal parameters for a relay network, for each annulus of VSN, an adaptive recursive Simpson’s algorithm is needed to calculate the lifetime of VSN. Assuming that complexity of the adaptive recursive Simpson’s algorithm is O(Lsimpson) and complexity of VSN cost computing is O(C). Then, O(k ×Lsimpson + C) complexity for different N and σx, σy is needed. Thereforecomplexity of algorithm 1 is O(Nmax × ×
× × (k × Lsimpson + C) + Mmax). Based on the analysis in Lemma 1, we finally have complexity ofAlgorithm 1" target="_self"> Algorithm 1 represented as O(Nmax ×
× (k × Lsimpson + C) + Mmax). Based on the analysis in Lemma 1, we finally have complexity ofAlgorithm 1" target="_self"> Algorithm 1 represented as O(Nmax × ×
× × k), which indicates thatAlgorithm 1" target="_self"> Algorithm 1 is a polynomial time computational complexity searching method.
× k), which indicates thatAlgorithm 1" target="_self"> Algorithm 1 is a polynomial time computational complexity searching method.
With Algorithm 2 the performance of our proposed deployment strategy is evaluated. Analysis parameters are also shown in Table 1. For Elliptical VSN, we compare our proposed strategy to uniform and Gaussian deployment strategies for different elliptical region, with major axes a and minor axes b are (a = 400, b = 200), (a = 500, b = 300), (a = 600, b = 400), and (a = 700, b = 500), respectively. Figure 13 compares the lifetime of


Algorithm 2. Global optimal parameters search algorithm for a Elliptical VSN.
three strategies VSN. Similar to Circular VSN analysis, we optimize the lifetime of VSN with cost $1915, $3465, $5860 and $8990. Then, with the same amount, we test that a uniform distribution strategy has the worst lifetime performance and optimized conventional one-tier Gaussian strategy lifetime performance is still worse than our proposed idea. For scenario in our analysis with parameters in Table 1, our two-tier strategy would prolong the lifetime of VSN by at least 6 times with the same cost.
After comparison of VSN lifetime, cost of VSN for maintaining certain period lifetime is analyzed in Figure 14. Continuing from the results of our earlier analysis, lifetime of VSN with our two-tier strategy are optimized

Figure 13. Lifetime comparison of two strategies with different region radius for Elliptical VSN.

Figure 14. Cost comparison of two strategies with different region radius for Elliptical VSN.
for 1250 hours, 841 hours, 663 hours, and 588 hours in four sample region. The costs of VSN in four monitored region using three strategies are shown in Figure 14. We note that our proposed strategy always shows smallest cost for VSN to maintain certain lifetime period and is able to keep the VSN cost increase slower than other two strategies when monitored region is increased. The uniform strategy normally needs the largest cost and cost increases quickly when the area of monitored region is increased. Gaussian strategy has a better performance in term of the cost than a uniform method. However, since it only deploys VNs, cost is wasted on extra VNs, which only provide packets forwarding function and camera hardware are not used.
Based on the Circular VSN results of the last subsection and Elliptical VSN analysis, we can conclude that our proposed two-tier deployment strategy always offers a better performance in term of the network lifetime and the cost than uniformly distributed deployment strategy and Gaussian distributed deployment strategies.
6.3. Division of Large Scale Wireless Visual Sensor Network
The algorithms described in last two subsections present an analytical method to optimize the parameters in VSN deployment strategy. For a small monitored region, we can choose a Circular VSN or Elliptical VSN to cover this area. Different types triangular shape could be fit by deploying half of Circular VSN or Elliptical VSN with the BS or sink node on the edge of monitored region. Then, optimal deployment parameters could be found with our proposed algorithms.
Based on the observation of our analysis, for keeping the same network performance, cost for VSN will increase exponentially as the area of region grows. Thus, it is unwise to keep the deployed VSN only as one network with the BS at the center of a large region. A large monitored region could be divided into multiple small area so that each small area could be covered by individual small VSN. Each small VSN could be formed with individual BS. Clustering technique could be used for dividing a large region VSN into small VSN clusters and one powerful cluster head nodes could function as a sink node, collecting data from RNs and VNs.
Figure 15 shows an example that one large monitored region is divided into seven small areas. Then, four of them is covered by Circular VSNs and others by Elliptical VSNs. Principle of region division depends on several factors such as sensing range, transmission range, region accessibility, security level, etc. For example, normally BS or sink node is not a battery-driven device. They need stable power supply and manual installation. If the region is not accessible by human or power supply is not available, it is impossible to install a BS or sink node at that location and division of the region need to be redesigned. Thus, region needs to be divided based on different monitoring tasks and specific situations.
7. Conclusion and Future Works
Lifetime and cost are two critical concerns for any large scale VSN deployment strategy. In this paper, we propose a novel two-tier VSN deployment strategy with minimal cost to prolong lifetime of VSN, which is limited by energy-hole problem. With tier-1 sensing network, we would deploy tier-2 relay network concentrically in the same region so as to help packets forwarding. Coverage and connectivity of Circular VSN and Elliptical VSN are analyzed with our disk and ellipse annuli mod-

Figure 15. Sample of large scale monitored region division.
eling. Then, we modeled our deployment strategy as a multi-objective problem that optimizes deployment parameters. Our evaluation shows that our strategy always has a better cost and lifetime performance than conventional uniform and Gaussian distribution strategies. Division of large scale VSN is presented at the end. Our future work is about analysis of large scale division scheme and optimal size of divided VSNs.
8. Acknowledgements
The authors would like to thank Dr. Weihuang Fu and Dr. Demin Wang for their helpful suggestions. The authors would also like to thank all the members of the Centre for Distributed and Mobile Computing (CDMC), for the countless interesting discussions and for creating such an excellent research environment.