Abstract

In this study, the reinforcement by screws for the wood perpendicular to the grain subjected to a rotational moment has been studied. For the estimation of rotational stiffness and yield moment, the reinforcement effect by the screws which varies depending on their position under the bearing plate was evaluated by taking the internal displacement distribution of the wood into account. The Finite Element Analysis (FEA) was used to investigate the internal displacement distribution of the wood. Then an appropriate function was found out to meet well with various internal displacement distributions under the bearing plate. The equations, which can estimate rotational stiffness and yield moment of the bearing performance of the wood reinforced by screws, were derived from the shear resistance mechanism between the screw and wood by considering their relative displacement distribution. Then rotational tests were carried out with the wood reinforced by the screws, setting screw thread at the various positions. Agreements between prediction and experimental results were very well. It was found that the screw reinforcement was effective, provided screw length should be longer for the wood height.

Keywords

Screw; Reinforce; FEA; Rotational Performance; Timber Structure

Share and Cite:

1. Introduction

The compression performance of wood perpendicular to the grain is remarkably inferior to that of wood parallel to the grain. In the case of the portal frame of through-bolt type as shown in Figure 1 (on the left), the end grain of the beam and the steel plate will be embedded in the side surface of column triangularly.

In order to improve the joint performance of timber structures, the enhancement of the bearing performance might be one of the possible choices. It is an effective method to insert the screws into the wood perpendicular to the grain as shown Figure 1. Therefore the studies on the screw reinforcement of bearing performance by inserting screws in the direction perpendicular to the wood grain has been carried out [1-3].

In reference [3], we have introduced a calculation method of stiffness and strength for screw reinforcement by considering the position of the thread of the screws. It was found that the effect of screw reinforcement varied depending on the position of screws thread. This was thought due to the inner displacement distribution on partial compression.

Since it was reported in the previous study [4] that there were outstanding differences on inner stress distribution of the wood depending on the cases subjected to uniform compression or triangular compression by the rotational moment, it was assumed that the tendency of inner displacement will not be the same for both cases. Although previous studies [1-3] focused on only uniform embedment case, as triangular embedment caused by moment resisting joint in portal frame structure has been getting interests among Japanese timber engineers recently, we intended to treat with triangular case.

In this study, assuming continuous column and column cut up to the same level as the upper surface of beam, the performance of the wood perpendicular to the grain deformed triangularly when they are received rotational moment was studied. Hereinafter we call them as continuous beam and cantilever beam respectively. It is because the stress distribution on the bearing area may be different depending on with and without the extend part of the wood. Then, the mechanical model with the screw reinforcement of rotational performance of the wood is proposed by considering the internal displacement distribution of the wood obtained by FEA.

2. Mechanical Model

In the case where the wood reinforced by the screws is subjected to rotational moment as shown in Figure 2, the resistance moment due to embedment resistance of wood (M_W) and that due to individual screw (M_S) are assumed to be independent. Hence, the total moment resistance can be expressed by Equation (1).

(1)

In Equation (1), M is the total moment resistance and n is the number of inserted screws.

Because M is the function of the rotational angle (θ), therefore, the total rotational stiffness (R) is obtained from rotational stiffness of the wood (R_W) and that of the screws (R_S) as shown in the Equation (2).

(2)

Ms can be expressed as multiplying the distance of the screw form the rotational centre (x_i) and the resistance force (P_S).

(3)

Then, θ can be expressed as below by using the displacement on the wood surface (δ_i) and x_i.

(4)

Then, R_S can be shown by using the P_S obtained from

previous study [3]. And, the displacement distribution of wood (δ_W) can be written as Equation (6).

(5)

(6)

Here, “a” and “b” are the positions on the vertical axis (z-axis) at the beginning and end of the thread. And ηis the function to decide the form of the displacement distribution and is obtained as follows.

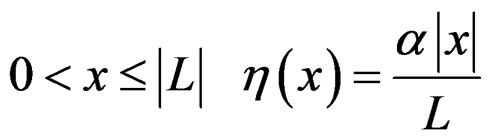(7)

In the case of the uniform embedment, the value of α in Equation (7) is denoted as mentioned in previous study [3]. While in the case of triangular embedment, the value of α must be different from uniform case. Therefore, FEA was carried out in order to obtain the value of α for triangular embedment in the next chapter.

The yield rotational angle can be defined as the deformation angle of the wood when whichever the screws or the wood reaches to the yield displacement earlier.

(8)

where: is the yield displacement of the wood. The yield strength (M_y) can be obtained by using the total initial stiffness (R) as follows.

(9)

3. Materials and Methods

3.1. Finite Element Analysis

3.1.1. Continuous Wood Beam

In order to decide the function of η, two-dimensional elastic analyses for the wood subjected to triangular embedment at the centre were conducted using commercially available FEA software “MSC’s Marc (Ver. 2011)”. Detecting influence of the distributions of δ_W, the width of the bearing plates, L was varied from 30 to 150 mm as a parameter.

The configuration of the wood analysed is shown in Figure 3. The centre of the wood was put between two rigid bodies and the wood forced to be deformed triangularly by letting two rigid bodies rotated with 0.001 rad, whose rotational centers were at the centers of the wood surface contacting with each rigid body. This moment makes triangle deformation to the wood. Since the internal displacement on the z direction at the any positions hardly changed even if the friction coefficient changed, the friction coefficient was set to zero which was easier for computation only to acquire the reinforcement effect of the screws.

Five different widths ranging from 0.3 to 1.5 times of the height (z₀) were modeled. The end distance was set at 400 mm, referring to report by Madsen [5]. Sitka Spruce (Picea sitchensis) was used for the specimen as the experimental verification. The material constants inputted into FEA are indicated in Table 1, referring to [6].

3.1.2. Cantilever Wood Beam

The configuration of the wood analysed by FEA is shown in Figure 4 in accordance with [5]. The edge distance in each condition is 400 mm. Five different widths ranging from 0.3 to 1.5 times of z₀ were modeled. The other test conditions are the same as those of the pervious clause.

3.2. Rotation Tests

3.2.1. Continuous Wood Beam

The steel frame used for the rotational test of the wood is

Conflicts of Interest

The authors declare no conflicts of interest.

References