Solvability of Inverse Eigenvalue Problem for Dense Singular Symmetric Matrices ()
1. Introduction
The inverse eigenvalue problem (IEP) involves the reconstruction of a matrix from prescribed spectral data. In order to limit the number of usually infinitely many solutions that are usually possible, if a solution does exists, it is usually required that the matrix constructed preserves a specific structure in addition to the spectral requirement. The nonnegative inverse eigenvalue problem (NIEP) is a special case of the IEP first posed by Kolmogorov in 1937. It involves the determination of the existence of entrywise nonnegative matrices when given a set of complex numbers that make up the spectrum of the yet to be determined matrix. The extensions and related conditions have been solved in several different ways. We give a brief review of results for the general inverse eigenvalue problem (IEP) and NIEP, as related to our work. A detailed treatment can be found in [1]. We begin with a realization criterion provided by Soto [2] for the NIEP. This result is based on conditions derived by Fiedler [3] and Borobia [4]. A list of real numbers  is said to be realizable if it forms the spectrum of an entry wise nonnegative matrix.
is said to be realizable if it forms the spectrum of an entry wise nonnegative matrix.
Theorem 1. Let  be a set of real numbers such that
be a set of real numbers such that

If there exits a partition  with
with






and for  odd
odd


and

satisfying

then  is realizable (by a nonnegative matrix with constant row sums).
is realizable (by a nonnegative matrix with constant row sums).
It has been proved that the above theorem is sufficient for the existence of an  symmetric nonnegative matrix with real spectrum
symmetric nonnegative matrix with real spectrum , see [2].
, see [2].
Recently Wu studied the IEP and gave the solvability criterion for its solution given a spectrum of complex numbers in the following two theorems [5].
Theorem 2. For a given list of complex numbers,  , if it has closed property under complex conjugation, that is
, if it has closed property under complex conjugation, that is  contains an element and its complex conjugation, then there must be at least one real matrix A with spectrum
contains an element and its complex conjugation, then there must be at least one real matrix A with spectrum .
.
Proof. By the closed property of  under complex conjugation, construct the polynomial:
under complex conjugation, construct the polynomial:
 (1)
(1)
By multiplying out, combining similar terms, and simplifying, the above equation can be written as:

where  are real numbers. It follows that
are real numbers. It follows that  are real numbers and the polynomial (1) has zeros
are real numbers and the polynomial (1) has zeros . Thus, using
. Thus, using , the matrix
, the matrix  can be constructed as:
can be constructed as:

It is straightforward to show that  has spectrum
has spectrum .
. 
Theorem 3. Given a list of real numbers  , the sufficient condition that there exists at least one nonnegative matrix A with spectrum
, the sufficient condition that there exists at least one nonnegative matrix A with spectrum  is that
is that  has the following properties
has the following properties

Several other results have been obtained for the inverse eigenvalue problem for Hermitian matrices (see for example [6]). It is obvious from the above theorems and the references that the solution of the IEP or even the NIEP is not unique. In addition, most of the solutions provided in the literature yield only sparse matrices. In this paper, we provide conditions for the solvability of the IEP for singular symmetric matrices. We show that unique solutions exist for matrices of rank one and give the solutions for dense matrices of rank greater than one.
2. Preliminaries
In what follows, we denote the  singular symmetric matrix
singular symmetric matrix  such that
such that  by
by . Without loss of generality, singularity is achieved by multiplying the first row by prescribed scalars. We denote a singular symmetric matrix of rank r by
. Without loss of generality, singularity is achieved by multiplying the first row by prescribed scalars. We denote a singular symmetric matrix of rank r by . In this case we write
. In this case we write  to denote that the
to denote that the  row is k times the first row, where
row is k times the first row, where . Finally, we denote the spectrum of
. Finally, we denote the spectrum of  by
by . If the rank of A is r, then we assume
. If the rank of A is r, then we assume  for
for , but
, but ,
, .
.
Lemma 1. Let A be a singular symmetric matrix of rank r. Then there exits an isomorphism between the elements of A and its distinct non-zero eigenvalues if and only if rank .
.
Corollary: The inverse eigenvalue problem has a unique solution for singular symmetric matrices of rank 1 and any prescribed row multiples.
We begin by considering . By definition,
. By definition,  is of the form:
is of the form:

Let  Since
Since  is singular of rank 1, it follows that
is singular of rank 1, it follows that . We have:
. We have:
 . Therefore
. Therefore .
.
Hence:
 (2)
(2)
Thus  has been reconstructed for given
has been reconstructed for given  and prescribed scalar k.
and prescribed scalar k.
We see from this formula that for any given  and parameter k, we can generate any 2 × 2 singular symmetric matrix of rank one. For example if
and parameter k, we can generate any 2 × 2 singular symmetric matrix of rank one. For example if ,
,  , we have
, we have

3. IEP for Dense Singular Symmetric Matrices
We generalize the method above in the following two theorems, first for an  singular symmetric matrix of rank 1 and then of rank
singular symmetric matrix of rank 1 and then of rank , where
, where .
.
Theorem 4. Given the spectrum and the row dependence relations ,
,  , where the
, where the ’s are nonzero real numbers, the inverse eigenvalue problem for a
’s are nonzero real numbers, the inverse eigenvalue problem for a  singular symmetric matrix of rank 1 is solvable.
singular symmetric matrix of rank 1 is solvable.
Proof. Given the spectrum , since rank
, since rank , it follows from our notation above that
, it follows from our notation above that  and
and ,
, . Let
. Let ,
,  be the row multiples. Letting
be the row multiples. Letting

Then
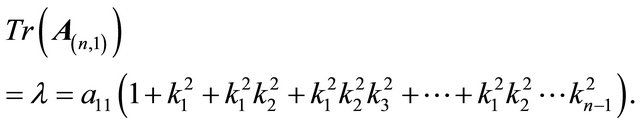
Hence

We note that for , Equation (2) shows that
, Equation (2) shows that
 . Thus by writing the matrix
. Thus by writing the matrix , the result follows by induction on
, the result follows by induction on .
. 
We state the following theorem for the general case where  has rank
has rank .
.
Theorem 5. The inverse eigenvalue problem for an n × n singular symmetric matrix of rank r is solvable provided that n − r arbitrary parameters are prescribed.
Proof. Let , where
, where . It is obvious that,
. It is obvious that,

where

and
 (3)
(3)
 such that
such that  where
where ,
,  and
and  is the
is the  row of
row of .
.
 . We see that for
. We see that for :
:

 :
:

 :
:

 :
:

The result follows for any rank .
. 
4. Numerical Examples
In this section, we illustrate the results above with small matrices of size  of rank
of rank . We begin with the singular 3 × 3 symmetric matrix of rank 1,
. We begin with the singular 3 × 3 symmetric matrix of rank 1,  , which is of the form:
, which is of the form:
 .
.
For ,
,  ,
,  , we have:
, we have:

Similarly, given ,
,  and
and , we obtain the following singular symmetric matrix:
, we obtain the following singular symmetric matrix:

In this case, . When
. When ,
,
 ,
,  and
and , we obtain the following 4 × 4 singular symmetric matrix of rank one:
, we obtain the following 4 × 4 singular symmetric matrix of rank one:

Obviously, the two examples given above can easily be verified for density, symmetry, rank, and that they satisfy the prescribed spectrum. Only the nonzero eigenvalue and the k’s have to be known for the solution of this type of IEP. As such, for given nonzero eigenvalue and k’s, the solution is unique.
The examples below clearly illustrate Theorem 5. For an n × n singular symmetric matrix of rank r, n − r arbitrary values must be prescribed in addition to the nonzero spectrum for the IEP to be solvable. This clearly leads to infinitely many solutions. We illustrate this with the following examples beginning with the IEP for n × n singular symmetric matrices of rank 2.  is of the form:
is of the form:

Here,  and
and
 . Hence
. Hence . Thus
. Thus

which yields  and
and . Therefore
. Therefore 
becomes a free variable. When ,
,  ,
,  and
and , for example, we obtain the following singular symmetric matrix:
, for example, we obtain the following singular symmetric matrix:

In general, the solution of the IEP for  leads to the solution of an rth degree polynomial equation in
leads to the solution of an rth degree polynomial equation in  of the form:
of the form:
 (4)
(4)
To solve the case for  and
and , we deduce from the general polynomial equation above that the following quadratic in
, we deduce from the general polynomial equation above that the following quadratic in  holds:
holds:

This yields: ,
,  and a14 becomes a free variable. For
and a14 becomes a free variable. For ,
,  ,
,  ,
,  and
and , we obtain a singular symmetric matrix below:
, we obtain a singular symmetric matrix below:

Similarly, for , we obtain the following quadratic in a11:
, we obtain the following quadratic in a11:

The solution gives:  and
and
 where
where  is a free variable. When
is a free variable. When ,
,  ,
,  ,
,  ,
,  and
and , we obtain a singular symmetric matrix below:
, we obtain a singular symmetric matrix below:

By the same method,  leads to the following cubic equation:
leads to the following cubic equation:

Solving the above cubic equation we obtain the following roots. ,
,  and
and
 where
where ,
,  and
and  are free variables.
are free variables.
Finally, we want to consider 5 × 5 singular symmetric matrix of rank 4. Using Equation (2), we obtain the following quartic equation in  where
where ,
,  ,
,  and
and  are the nonzero members of the spectrum.
are the nonzero members of the spectrum.
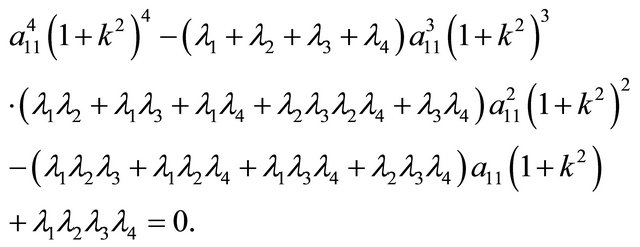
Factoring the above quartic equation, we obtain the following results: ,
,  ,
,  and
and
 . The free variables are
. The free variables are ,
,  ,
,  ,
,  ,
,  and
and .
.
As an example, if we let 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and 

We provide in the appendix, a program that generates any dense n × n singular symmetric matrix of rank 1 for given row multipliers. The program could be easily modified for rank .
.
5. Summary and Discussion
The IEP has a variety of applications which include control design, system identification, principal component analysis, geophysics and mechanical systems. Several interpretations and applications of the IEP have been considered. However, the direct IEP involving full matrices has received relatively less attention owing to the intractability of the problem for even small sized matrices. In this paper, we focused on the IEP for dense singular symmetric matrices. We showed that while unique solutions exists for an n × n matrices of rank 1, infinitely many solution exist for n × n singular symmetric matrices of rank r, where . With our method, an extension to nonsingular matrices for small n, could become feasible via a numerical analytic interpretation of the IEP.
. With our method, an extension to nonsingular matrices for small n, could become feasible via a numerical analytic interpretation of the IEP.
6. Acknowledgements
The authors Kwasi Baah Gyamfi and Joseph AckoraPrah are grateful to Eastern Connecticut State University for the resources provided at the Department of Mathematics and Computer Science to enable them to complete this research. Anthony Y. Aidoo acknowledges with gratitude the support received from 2001 CSU Research Grant for this work.
Appendix
The following program generates an n × n singular symmetric matrix of rank 1 function ()
%UNTITLED2 Summary of function goes here % Detailed explanation goes here lambda=input('Enter a positive number as trace of the generalized matrix')
k = input('1.Enter m positive numbers that characterize the generalided matrix')
m = length(k);h(1)=1;ss=[];
for i=1:m h(i+1)=h(i)*k(i);
end h;kk=1;
for i=m:-1:1 kk=kk*(k(i)^2)+1;
end kk;
format short eng a=lambda/kk ss=a*h;
mm(1,:)=ss;
for i=2:(m+1);
mm(i,:)=k(i-1)*mm((i-1),:);
end mm %fprintf('The required singular matrix of rank 1 is:\n %d \n',mm)
tr=trace(mm)
NOTES