Wireless Power Transmission into a Space Enclosed by Metal Walls Using Magnetic Resonance Coupling ()
1. Introduction
1.1. Wireless Power Transmission to a Space Closed with Metal
Accidents attributable to deteriorated infrastructure are becoming severe around the world. Automatic diagnosis devices for old infrastructure powered by wireless transmission have been investigated for solving this problem at low cost. Kuroda [1] proposed a wireless-powered inspection robot for laying pipes using the electromagnetic induction in an electric power plant.
As described herein, wireless power transmission using magnetic resonance coupling is proposed for a space enclosed by metal walls. This method can be applied as a power supply for sensors and devices in a metal pipe or over metal walls, as shown in Figure 1.

Figure 1. Images of wireless power transmission applications though a metal wall.
1.2. Magnetic Resonance Coupling
Magnetic resonance coupling is a wireless power transmission method that achieves high transmission efficiency using resonant circuits in a transmitter and a receiver [2,3]. This method is applicable even with low mutual coupling between the transmitter and receiver. Therefore, many applications are expected in various fields, such as electric vehicles [4], mobile devices [5], micro-robots [1], medical sensors and implantable devices [6,7].
Transmission efficiency depends on two parameters: 1) coupling coefficient k between a transmitter and a receiver is determined by their distance, mutual attitude, size, and shape; 2) quality factor Q of the transmitter and receiver is a ratio of energy loss such as Joule loss to energy stored in resonators. In magnetic resonance coupling, the resonance frequency is usually chosen in the kHz-MHz range to obtain a high quality factor of several hundred. When a product kQ is 10, transmission efficiency of 80% is achievable over a centimeter gap.
2. Magnetic Shielding by Metal
At a high AC frequency, large eddy current is induced on a metal plate. It shields magnetic fields generated by a resonator, as shown in Figure 2. Thereby, magnetic resonance coupling at MHz frequencies would be extremely difficult over metal walls.
Mizuno [8] proposed magnetic resonance power transmission into a metal pipe using an electrically isolating slit on the pipe, where the slit plays a role as a “repeater.” However, this method is applicable only to extremely limited cases, as when the pipe has been fabricated with a slit beforehand.
In this study, wireless power transmission to a space enclosed by metal walls at low resonant frequency was proposed and demonstrated. Deep penetration of magnetic fields into metal is expected at the power source AC frequency of 50 Hz, which is the frequency of our commercial power supply. Although Zangl [9,10] sought to transmit power into a metal pipe by electromagnetic induction at 50 Hz, transmission efficiency was not examined specifically. In this study, transmission efficiency is improved markedly by magnetic resonance coupling.
3. Transmission System
3.1. Fabrication of High-Q Resonators
Transmitter and receiver resonators with resonance fre-

Figure 2. Depth of penetration into metal.
quency of 50 Hz were designed and fabricated as shown in Figure 3 and Table 1. They comprise a solenoid coil and a core made of multilayered electric steel sheets. Their designed quality factor was several tens irrespective of the low resonance frequency of 50 Hz because the inductance was enhanced by a core. The resonance frequency was adjusted to 50 Hz by varying the number of coil turns. A switching AC power supply was used in the experiment.
Measured Q is shown in Table 2 with estimated values. Core loss and copper wire loss were considered for estimation, but radiation loss was neglected because the coil wire length was sufficiently short compared with the AC field wavelength. Although magnetic flux density in the core was assumed as uniform for estimation, it is not uniform in reality, as shown in Figure 4, resulting in discrepancy between measured and estimated values.
AC frequency must be regulated to coincide with the resonance frequency of resonators unlike conventional electromagnetic induction. When Q is 30, AC frequency fluctuation is required below 3% in order to achieve effective resonance coupling.

Figure 3. Photograph of the receiver resonator.

Table 2. Quality factor of the resonators.
Measured coupling coefficient k is shown with the distance between the resonators in Figure 5, where the solenoid axes were aligned in parallel.
3.2. Relation of Magnetic Flux Saturation and Quality Factor
A high Q is available by lengthening the core and reducing the cross-sectional area of the core. However, the current in resonators is limited because of magnetic flux density saturation. The saturation magnetic flux density is 1.9 T in the oriented electric steel sheet. Because the magnetic flux density approaches the saturation density, coil inductance is decreased and the resonance frequency changes. Here, the maximum allowable current is defined as that which is detected when the resonance frequency changes by 1%.
Because larger current flows in the transmitter resonator than in the receiver resonator, the transmitter core must be designed as thicker than the receiver core to avoid saturation. The transmitter resonator core thickness is 7 mm. That of the receiver resonator is 5 mm. The maximum allowed current was estimated using a commercial electromagnetic simulator, Femtet, as shown in

Figure 4. Computed magnetic flux density distribution in the core. Receiver resonator, current 1.7 A.

Figure 5. Measurement coupling coefficient k.
Figure 4 and Table 3. Circuit analysis shows that the maximum allowable current of 2.2 flows in the transmitter resonator when k is 0.7 and the load power consumption is 3 W. Under these conditions, the expected receiver resonator current is 1.4 A, with a margin of 0.3 A.
3.3. Resonant Circuits
In a resonator circuit, a capacitor can be connected in series or in parallel. In the transmitter, a capacitor was connected in serial. Equation (1) shows the theoretical transmission efficiency when a parallel-capacitor resonator is used for the receiver, as shown in Figure 6(a), whereas Equation (2) shows the efficiency when a serial-capacitor resonator is used for receiver as shown in Figure 6(b) [11,12].
 (1)
(1)
 (2)
(2)
Here, QT and QR respectively denote the quality factors of the transmitter and receiver resonator. Impedance ratio rR is defined as rR = Z0ld/Rr, where Rr is the resistance in the receiver resonator and Z0ld is the load impedance. Optimum impedance ratio rR,opt achieves the maximum transmission efficiency for given k as shown in Figures 7 and 8.

Table 3. Maximum allowable current in the resonators.
 (a)
(a) (b)
(b)
Figure 6. Diagram of resonant circuits. (a) Series-parallel resonant circuits; (b) Series-series resonant circuits.

Figure 7. Receiver impedance ratio and transmission efficiency (transmitter, serial; receiver, parallel).
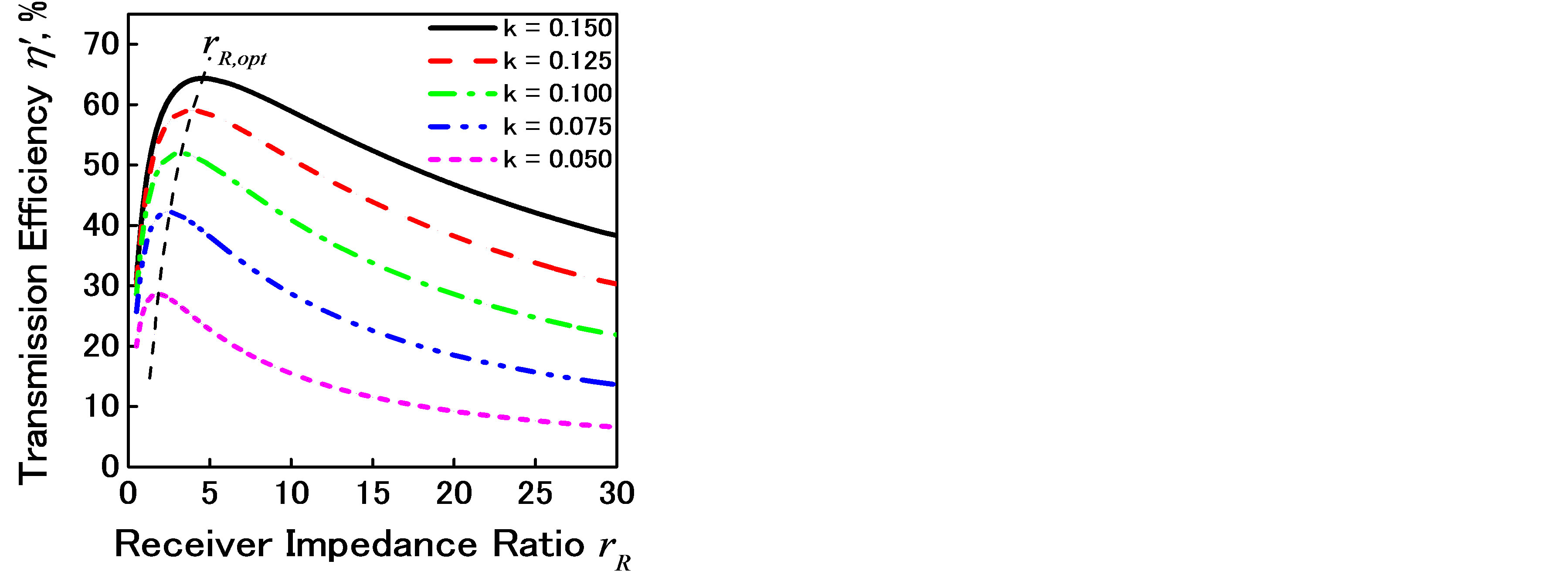
Figure 8. Receiver impedance ratio and transmission efficiency (transmitter, serial; receiver, serial).
In our demonstrations, a series-parallel circuit was chosen because the impedance ratio lies between 250 and 500. In addition, when a parallel resonator is used as a receiver, a voltage drop loss in the rectifier is small because of the high load voltage.
4. Power Transmission Demonstration to a Space Closed by Metal Walls
Figure 9 shows setups of transmission demonstration into a box-shaped metal closed space and into a metal pipe. LEDs were used as a load. For rectification, a diode bridge rectifier circuit and a smoothing capacitor were used. A single-phase auto input-transformer was used for input impedance matching.
Figure 10 presents the relation between transmission efficiency and transmission distance for the case into the metal box. The estimated efficiency using Equation (1) and the measured efficiency are in good agreement. Figure 11 shows the relation between the transmission efficiency and misalignment displacement in the coil axis direction. The distance was normalized by the
 (a)
(a) (b)
(b)
Figure 9. Photographs of demonstration setup. (a) Transmission into a space enclosed by metal walls; (b) Transmission into a metal pipe.

Figure 10. Transmission efficiency and transmission distance.
length of the transmitter resonator, which is 211 mm in this case. As the figure shows, the misalignment effect is small. The effect is also negligibly small in the direction perpendicular to the coil axis.
Figure 12 presents the relation between transmission efficiency and the SUS wall thickness, which was changed by piling up multiple 1-mm-thick SUS plates. The metal thickness was normalized by the depth of penetration into metal, which is 60.4 mm at 50 Hz. The transmission efficiency decreased monotonically with wall thickness and showed a 20% decrease from the nowall condition when the wall thickness was 16% of the depth of penetration.
Experimental conditions and results are presented in Table 4. Transmission efficiency of 43% was achieved through a 1.0 mm SUS plate and that of 10% into a metal pipe of 5.0 mm thickness.

Figure 11. Transmission efficiency and misalignment displacement in the coil axis direction normalized by the transmitter resonator length.

Figure 12. Transmission efficiency and wall thickness normalized by depth of penetration that is 60.4 mm at 50 Hz.

Table 4. Demonstration conditions and results.
5. Conclusions
Wireless power transmission to a space enclosed by metal walls was shown using magnetic resonance coupling at the resonance frequency of 50 Hz. Transmission efficiency of 43% was achieved through a 1.0 mm SUS plate and of 10% into a 5.0-mm-thick metal pipe.
Magnetic resonance coupling at AC frequency of 50 Hz can be used to transmit power into a metal pipe or over a SUS metal plate of several millimeters.
In the resonator design, a multilayered electric steel sheet was used as a core to enhance inductance. Transmission power was limited by the maximum allowable current to avoid magnetic flux density saturation in the core.
A parallel capacitor connection was used because optimum impedance ratios are 250 - 500, which match those of this demonstration system, and because high load voltage is expected, resulting in a small voltage drop loss in the rectifier.