Symmetric Identities from an Invariant in Partition Conjugation and Their Applications in q-Series ()
1. Definitions and Combinatorial Interpretations
We shall first present some basic definitions and combinatorial interpretations for basic hypergeometric series and integer partition. For simplicity, unless stated otherwise we shall assume that 
is a nonnegative integer and
, let
Definition 1.1 For any integer n, the q-shifted factorial is defined by
Definition 1.2 A partition 
of a positive integer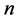 
is a finite nonincreasing sequence of integers
, such that
. 
is the conjugate partition of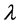
. The largest part, the number of parts, as well as the sum of the parts are denoted by
, 
and
, respectively.
An effective device for studying partitions is the graphical representation. For a partition
, its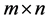 
Durfee rectangle is the maximum rectangle contained in the Ferrers diagram of
. Conjugation and the several invariants have been used in a variety of ways over the years, see Andrews’s encyclopedia [2] . It is worth pointing out that there is a fundamental invariant which despite its simplicity has not received too much attention. This is
, the number of different parts of
. For all partitions 
and its conjugation
,
(1)
In this paper, we shall show how (1) could be used to obtain a series of symmetric identities by studying modified Durfee rectangles. Consider the expansion
We interpret this as an expansion involving only one part, namely
, where the power of 
records
, while that of 
indicates whether the part occurs or not. Thus, we interpret
(2)
as the generating function of partitions 
into parts less than or equal to
, such that the power of 
records
, while that of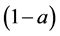 
indicates
. Then it follows that the three-parameter generating function for all unrestricted partitions
, namely, the function
(3)
We consider all partitions 
for which
. This accounts for the term 
in (3). Since 
contains 
as a part, we have the factors 
and 
in the numerator. The part 
may repeat, which is given by
. The repetition of 
will not contribute to 
and so there is no further power of
contributed by the part
. The part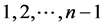 
could repeat and their contribution to the generating function is given by the term
Formula (3) follows.
2. Symmetric Expressions for 
In this section, we give several symmetric expansions for 
via modified Durfee rectangles analysis of partition.
Theorem 2.1
Proof. For every partitions 
and
, the Ferrers graph contains a largest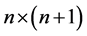 
Durfee rectangle with side 
horizontally by 
vertically. Then to the right of the Durfee rectangle, we have a partition 
which has at most 
parts, or equivalently, 
, the conjugate of
, with largest part
. Below the Durfee rectangle we have a partition 
whose parts
. We now divide our consideration into four cases.
1) 
We consider the contribution of the partition 
to 
by utilizing its conjugate
.
The factor 
in the numerator arises from the column of length 
lying to the right of the Durfee rectangle. Because 
contributes nothing to
, we omit
.
The contribution of the partition 
to 
is
Note that the parameter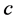 
is absent because the partition 
has no contribution to
.
Meanwhile, the contribution of the modified Durfee rectangle to 
is
Thus, we derive the generating function of every unrestricted partitions
:
2) 
The generating function of every unrestricted partitions
:
3) 
The generating function of every unrestricted partitions
:
4) 
The generating function of every unrestricted partitions
:
Summing these four generating functions for
, we get an expression for
:
Remark 2.2 Under partition conjugation, 
and 
are interchanged, it follows that 
and 
are symmetric in
.
Theorem 2.3 From formula (3) and the symmetry of 
and
, we have
(4)
(5)
Theorem 2.4 From Theorem 2.1 and the symmetry of 
and
, we have
(6)
(7)
(8)
where (8) results from the 
Durfee square analysis.
3. The Applications of the Symmetric Identities in q-Series
In this section, we shall explore the extensive applications of formulas (4) to (8) in 
-series. Without too much effort one can obtain much well-know knowledge as well as new formulas by proper substitutions and elementary calculations. It will be overly clear that the list of nice application is sheer endless.
3.1. Symmetric Identities
From (4) and (5), we get the following beautiful symmetric identity.
Corollary 3.1
(9)
Taking 
in (9), we derive the following identity, from which Liu [3] proved an identity of Andrews.
Corollary 3.2
(10)
Setting 
and then taking 
in (4) and (5), we have
Corollary 3.3
(11)
which was first stated and proved by N. J. Fine [4] . Andrews derived it combinatorially from the consideration of partitions without repeated odd parts in [5] .
3.2. Mock Theta Functions
In his famous last letter to Hardy [6] , Ramanujan introduced 17 mock theta functions without giving an explicit definition, among which, one third order mock theta function is as follows
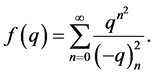(12)
In 1966, Andrews [7] defined the following generalization of 
(13)
Moreover, Watson [8] added three functions to the list of Ramanujan’s third order mock theta functions and the following identity is just one of them
By proper substitutions in Theorem 2.3 and 2.4, we obtain much simpler expressions for the above mock theta functions. Through the specializations 
and 
in (4) and (8), we derive a simpler transformation formula for
:
Corollary 3.4
(14)
Taking 
in (14), a representation for 
follows, with the powers diminished
(15)
Fine [1] first derived (15) by applying some transformation formulas and Liu [[9] , Theorem 3.7] proved it combinatorially by an application of involution. Changing 
to 
and then putting 
in (4) and (6), we get a new expression for
, with the powers diminished:
Corollary 3.5
(16)
3.3. A Two-Variable Reciprocity Theorem
Taking 
and then letting 
in (4), we have
In his lost notebook [10] , Ramanujan offers a beautiful reciprocity theorem
(17)
After the same substitutions in (5) and (7), respectively, we get
Corollary 3.6
(18)
(19)
Formula (18) is a slightly simpler representation of
. From (19) and the above reciprocity theorem (17), we get the following two variable generalization of the Quintuple Product Identity [[11] , Theorem 3.1] without any proof:
Corollary 3.7 A Two-Variable Generalization of the Quintuple Product Identity
For
, 
,
(20)
3.4. Identities from Ramanujan’s Lost Notebook
By special substitutions, we could go through a series of important Entries in Ramanujan’s Lost Notebook [12] . We take several of them as examples, for their combinatorial proofs, see [13] . The function
is defined by Ramanujan. Setting 
and then letting
, then (4) and (6) can be reduced to
Corollary 3.8 (Entry 9.2.2)
The same substitutions in (4) and (8), we have
Corollary 3.9 (Entry 9.2.3)
Putting 
and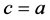
, and then setting 
in (4) and (8), we have
Corollary 3.10 (Entry 9.2.4)
For the above identity, it is interesting to note that the terms in 
and 
on the right side are the same as those on the left side, but with the powers diminished. In (4) and (6), we replace 
by 
and take 
and
, and then set
, the Entry 9.2.5 in Ramanujan’s Lost Notebook [12] follows:
Corollary 3.11 (Entry 9.2.5)
Berndt and Yee [13] proved the above two corollaries combinatorially by accounting for partitions into distinct parts. Replacing 
by 
and taking 
and 
in (4) and (6), then we get the following Entry. Berndt and Yee [13] derived it by employing 
-modular partitions.
Corollary 3.12 ( Entry 9.3.1)
In (4) and (6), we take
, and then set
, Entry 9.4.1 follows:
Corollary 3.13 (Entry 9.4.1)
(21)
This identity was derived from Franklin involution by Berndt and Yee [13] and was also got from two entries by Warnaar [14] , where analytic methods were employed.
3.5. Further Consequences
Corollary 3.14
(22)
Proof. Taking
, and then letting 
and 
in (4) and (8), we have
(23)
Identity (22) is a false theta series identity. Results like these were studied by L. J. Rogers [15] , however, the elegant result appears to have escaped him. Andrews [16] proved identity (22) by using three transformation formulas and showed that (22) implied a partition identity like that deduced from Euler’s Pentagonal Number Theorem ([2] , p. 10).
Taking 
and 
in (4) and (5), we generalize the not at all deep but elegant identity:
Corollary 3.15
(24)
Taking
, and then setting
, (4) and (8) can be reduced to the famous Gauss triangle series
Corollary 3.16
(25)