Experimental Study of Two Impinging Jets Aligned With a Crossflow ()
1. Introduction
Turbulent jets impinging on flat surfaces through a low-velocity crossflow are typical in impingement cooling applications in industry, as well as of the flow beneath a short/vertical take-off aircraft which is lifting off or landing with zero or small forward momentum. Ground effect may occur and change the lift forces on the aircraft, cause reingestion of exhaust gases into the engine intake and raise fuselage skin temperatures. In this latter application the impingement of each downward-directed jet on the ground results in the formation of a wall jet which flows radially from the impinging point along the ground surface. The interaction of this wall jet with the free stream results in the formation of a ground vortex far upstream of the impinging jet, which has profound implications on the aircraft design [1] [2] . In addition the collision of the wall jets originates a fountain upwash flow, affecting the forces and moments induced in the aircraft when operating in ground effect. Improved knowledge of impinging flows is therefore necessary to avoid these effects and to be able to model a range of jet-impingement type of applications with practical interest.
This paper presents a detailed analysis of the complex flow field beneath twin jets through a low-velocity crossflow and provides a quantitative picture of the main features of interest of impingement type of flows. The results include laser-Doppler velocity measurements of flow characteristics, which are complemented by flow visualization.
Earlier detailed measurements of the flow properties of fountain upwash are scarce and have been presented essentially in the absence of a crossflow and with the use of probe techniques. The most relevant works have been reviewed by [3] and [4] , and indicated high turbulence levels and spreading rates in the fountains [5] [6] . Different interpretations of the measurements were presented by [7] and [8] due to the difficulties in measuring complex flows using hot-film and pitot-probe techniques. Ref. [9] and [10] also presented flowfield and pressure data for twin-rectangular jets for small jet-to-crossflow velocity ratios (<10). Ref. [4] reports laser Doppler velocity (LDV) measurements, including those of shear stress, for axisymmetric impinging jets with S/D = 9 and 14 and H/D = 3 and 5.5, but again the existence of a crossflow was not considered. Detailed measurements of the velocity characteristics of normal impinging jets on a flat surface can be more easily found for single jet configurations for relatively large impingement heights and normally for H/D > 10, using either probe and optical techniques, as reviewed for example by [3] and [11] . Experiments on the aerodynamics of jets through a confined crossflow are much scarcer, and have only been reported for large impingement heights and for low velocity ratios between the jet and the crossflow Vj/Uo. These works have therefore only peripheral relevance to the VSTOL ground effect problem. Ref. [12] -[14] report hot-wire measurements for ratios H/D greater than 24 and for values of Vj/Uo respectively up to 1.95, 2 and 16. Ref. [15] presents results for H/D = 12 and [16] gives Pitot-tube measurements for values of H/D = 3.05 and for jet-to-crossflow velocity ratios up to 6.8. Ref. [17] reports LDV measurements, including those of shear stress, but for values of H/D = 12 and for velocity ratios up to 2.3. Only [3] provided detailed LDV measurements for a single jet configuration for a jet Reynolds number of Rej = 6 × 104, a velocity ratio between the jet and the crossflow of 30, 42 and 73 for the jet exit 3, 4 and 5 jet-diameters above the ground plate. The measurements include time-resolved velocity characteristics along the horizontal and vertical directions, and respective correlations, in planes parallel to the jet nozzle axis [18] [19] . Ref. [20] and [21] extended their study to multijet impinging configurations producing upwash fountain flows, which are the heart of the complicated effects by VSTOL aircraft when they operate in ground proximity, but as far as twin jets are concerned only the geometry with the jets side by side was considered. In the present work the twin jets are aligned with the crossflow, which is the geometry relevant for the next generation of VSTOL aircraft JSF (Figure 1).
The remainder of this paper is presented in four sections. Section 2 describes the experimental configuration and measurement procedure, gives details of the laser-Doppler velocimeter and provides assessments of accuracy. The arguments associated with these assessments are based on previous experiments and are presented in condensed form. Section 3 presents the experimental results obtained in the vertical plane of symmetry containing the axis of both jets and quantifies the mean and turbulent velocity characteristics of the flow. The final section summarizes the main findings and conclusions of this work.
2. Experimental Work
The wind tunnel facility designed and constructed for the present work is schematically shown in Figure 2. During all the design process, especially for the boundary layer part of the flow, were followed the recommendations of [22] for open circuit wind tunnels. A fan with 15 KW nominal power drives a maximum flow of 3000 m3/h through the boundary layer wind tunnel of 300 × 302 mm exit section. Each jet unit of 15 mm inner diameter is mounted vertically in the top of the test section with the axis contained in the vertical plane o symmetry parallel to the crossflow.
The origin of the horizontal, X, and vertical, Y, coordinates is taken at the midpoint between the centers of the
![]()
Figure 1. Representation of the ground vortex flow phenomena adapted to the JSF F-35 Variant B.
jets exit. The X coordinate is positive in the direction of the wind tunnel exit and Y is positive upwards.
The present results were obtained at the vertical plane of symmetry for jet mean velocities of Vj = 36 m/s and mean crossflow velocity of U0 = 1.6 m/s, corresponding to a velocity ratio, VR = Vj/Uo of 22.5.
The velocity field was measured with a two-color (two-component) Laser-Doppler velocimeter (DantecFlowlite 2D), which comprised a 10 mW He-Ne and a 25 mW diode-pumped frequency doubled Nd:YAG lasers, sensibility to the flow direction provided by frequency shifting from a Bragg cell at f0 = 40 MHz, a transmission and backward-scattered light collection focal lens of 400 mm. The half-angle between the beams was 2.8˚ and the calculated dimensions of the axis of the measuring ellipsoid volume at the e−2 intensity locations were 135 × 6.54 × 6.53 μm and 112 × 5.46 × 5.45 μm respectively (see Table 1 for details). The horizontal, U, and vertical V, mean and turbulent velocities were determined by a two-velocity channel Dantec BSA F60 processor. The seeding of the flow with glycerin particles of 0.1 - 5 μm was produced by a smoke generator. The transmitting
![]()
Table 1. Principal characteristics of the 2D Laser-Doppler velocimeter.
and collecting optics is mounted on a three-dimensional traversing unit, allowing the positioning of the center of the control volume within ±0.1 mm.
In order to measure the vertical components in near wall regions, the transmitting optics were inclined by half angle of beam intersection and the scattered light was collected off-axis. Measurements could then be obtained up to 0.5 mm from the ground plate without a significant deterioration of the Doppler signals. Results obtained 20 mm above the ground plate with both the on-axis and the off-axis arrangements have shown a close agreement, within the precision of the equipment.
Errors incurred in the measurement of velocity by displacement and distortion of the measuring volume due to refraction on the duct walls and change in the refractive index were found to be negligibly small and within the accuracy of the measuring equipment. Non-turbulent Doppler broadening errors due to gradients of mean velocity across the measuring volume may affect essentially the variance of the velocity fluctuations [23] , but for the present experimental conditions are of the order of  and, therefore, sufficiently small for their effect to be neglected. The largest statistical (random) errors derived from populations of, at least, 10,000 velocity values were of 0.5% and 3%, respectively for the mean and the variance values, according to the analysis recommended by [24] for a 95% confidence interval. No corrections were made for sampling bias, but no correlations were found between Doppler frequencies and time interval between consecutive bursts even in the zones of the flow characterized by the lowest particle arrival rates, suggesting that those effects are unimportant for the present flow conditions.
and, therefore, sufficiently small for their effect to be neglected. The largest statistical (random) errors derived from populations of, at least, 10,000 velocity values were of 0.5% and 3%, respectively for the mean and the variance values, according to the analysis recommended by [24] for a 95% confidence interval. No corrections were made for sampling bias, but no correlations were found between Doppler frequencies and time interval between consecutive bursts even in the zones of the flow characterized by the lowest particle arrival rates, suggesting that those effects are unimportant for the present flow conditions.
Systematic errors incurred in the measurements of Reynolds shear stresses can arise from lack of accuracy in the orientation angle on the normal to the anemometer fringe pattern, as shown in [25] , and can be particularly large in the vicinity of the zones characterized by zero shear stress: for the present experimental conditions the largest errors are expected to be smaller than −2.5%.
3. Results
In this chapter, experimental data obtained will be presented and discussed under two headings. First, flow visualization is presented, and then mean and turbulent velocity profiles are presented and discussed for the velocity ratios VR of 22.5.
3.1. Visualization
Flow visualization was performed using digital direct photography to guide the choice of the measurement locations and to provide a qualitative picture of the flow. The longitudinal vertical plane of symmetry was illuminated with a sheet of light. The photos were taken perpendicular to the vertical plane of symmetry. For all the flows studied, the results have shown (for each jet) a pattern similar to that of a single impinging jet. Figure 3 identifies the flow development along the vertical plane of symmetry, i.e. Z = 0. Each jet has an initial potential-core jet region, where the flow characteristics are identical to those of a free jet, and near the horizontal plate the impingement region, characterized by considerable deflection of the jet. It was not possible to identify all the regions simultaneously in the same photo, neither a deflection of each jet by the crossflow. The selected picture shows the wall jet corresponding to the upstream impinging jet which is almost parallel to the ground plate and exhibits a behavior similar to that of a radial wall jet where the upstream effects of interaction due to impingement are no longer important. The upstream wall jet interacts with the crossflow and forms a horseshoe vortex close to the ground plate, which wraps around both impinging jets. As a result, two streamwise counter-rotating vortices develop side-to-side and decay further downstream of each impinging zone forming a ground vortex. The nature of each ground vortex is similar to the horseshoe structure known to be generated by the deflection of a boundary layer by a solid obstacle [26] , but is different from the vortex pair known to exist in a “bent-over” jet in a crossflow far from the ground [13] . No evidence of a ground vortex corresponding to the downstream impinging jet could be confirmed, which is an indication that the upstream impinging jet and its ground vortex are blocking the crossflow and provoking an alteration to the flow pattern. If the jets were positioned side by side in front of the crossflowtwoground vortexes would appear as well as a fountain flow in the vertical plane of symmetry due to the collision of the two individual radial wall jets [20] [27] -[29] . In the present case for a velocity ratio between the jet and the crossflow of VR = 22.5 no fountain flow could be detected.
Analysis of Figure 4 also suggests that the crossflow is deflected sideways by the penetration of the jet and may cause a recirculation region just downstream of the discharge, away from the ground plate, but cannot be clearly identified. These features of the flow are quantified in Figures 5-7 through a detailed set of mean and turbulent velocity measurements obtained in the vertical plane of symmetry (Z = 0) for a Reynolds number
![]()
Figure 3. Geometrical arrangement of the jets.
![]()
Figure 4. Visualization of the twin jet flow in the vertical plane of symmetry for Rej = 4.3 × 104, Vj/Uo = 22.5, H/D = 20.1, and S/D = 6.
based on the jet-exit conditions of 4.3 × 104, a free stream to jet velocity ratio, VR = Vj/Uo of 22.5, a jet height to jet diameter ratio, H/D, of 20.1, and a spacing between the jets, S/D, of 6.
3.2. Measurements
Figure 5(a) and Figure 5(b) show vertical profiles of horizontal,  , and vertical,
, and vertical,  , mean velocity components along the vertical plane of symmetry (Z = 0).
, mean velocity components along the vertical plane of symmetry (Z = 0).
The mean horizontal velocity profiles at X/D = −2.93, −1.47, 0 and +1.47 show negative values near the ground (Y = 0) that correspond to the upstream wall jet, revealing that the first impinging jet was deflected by the crossflow. The impinging point of the first jet is located at about X/D = +2.93 in a position that is vertically near the axis of the second jet exit (X/D = +3), which is more strongly deflected due to this interference. As a consequence, the downstream wall jet of the first jet and the second jet seems to merge rapidly in a single flow in the crossflow direction. These profiles exhibit maximum positive (downstream) values of the mean horizontal velocity component between Y = 100 mm and 150 mm that reach twice the crossflow velocity. This result can also be confirmed with the help of Figure 5(b) that shows only positive values (upwards) of the mean vertical velocity component just 2D downstream of the geometrical axis of the second jet (X/D = +5.0). The second jet is still detected in the profile at X/D = +2.93 by the negative (downwards) values of , but only quite near of the upper wall for Y > 180 mm (Y/H > 0.596). This means that no upstream wall jet resulting from the second jet exists, but the complete jet is deflected by the crossflow. This result is consistent with the conclusions of [5] that found for a single impinging jet flow that the ground vortex blocks the passage of the confined crossflow increasing the velocity of the crossflow that passes over. So, for the configuration the final result is that the second jet “views” a smaller jet-to-crossflow velocity ratio and no impingement occurs. In the practical situation of a
, but only quite near of the upper wall for Y > 180 mm (Y/H > 0.596). This means that no upstream wall jet resulting from the second jet exists, but the complete jet is deflected by the crossflow. This result is consistent with the conclusions of [5] that found for a single impinging jet flow that the ground vortex blocks the passage of the confined crossflow increasing the velocity of the crossflow that passes over. So, for the configuration the final result is that the second jet “views” a smaller jet-to-crossflow velocity ratio and no impingement occurs. In the practical situation of a
VSTOL aircraft this may result in a different pressure distribution in the under surface of the aircraft, that with front wind or small forward movement may result in enhanced under pressures in the aft part of the aircraft causing a suction down force and a change of the pitching moment towards the ground.
Figure 6(a) and Figure 6(b) show horizontal transversal profiles of horizontal,  , and vertical,
, and vertical, 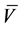 , mean velocity components, quantify the development of the impinging jets and confirm the above description of the flow. The measurements, and particularly those of the vertical velocity component, do not identify a centrally located fountain rising from the ground plate without interference from the main jets, as it occurs in practical VSTOL applications [29] . This result confirms our hypothesis that the alignment of the twin jets with the crossflow would create a special flow pattern not yet reported before. The wall jet resulting from the first jet flows underneath the second one, but the ground vortex formed upstream is only interfering away from the vertical symmetry plane.
, mean velocity components, quantify the development of the impinging jets and confirm the above description of the flow. The measurements, and particularly those of the vertical velocity component, do not identify a centrally located fountain rising from the ground plate without interference from the main jets, as it occurs in practical VSTOL applications [29] . This result confirms our hypothesis that the alignment of the twin jets with the crossflow would create a special flow pattern not yet reported before. The wall jet resulting from the first jet flows underneath the second one, but the ground vortex formed upstream is only interfering away from the vertical symmetry plane.
The mean vertical velocity component is always positive from the upper wall (Y/H = 1) up to the middle of the crossflow (Y/H = 0.5), confirming the conclusions drawn from the vertical velocity profiles in the lower part of the crossflow and discussed in the previous paragraphs.
The asymmetry of the flow can be confirmed from the horizontal profiles of the mean vertical velocity component with higher peaks up to 10% of the vertical velocity in the upstream side (X < −50 mm or 3.33D). The middle value between the maximum and the minimum of the mean horizontal velocity component or the mean vertical velocity components can be used to indicate the center of the jet, and in the upstream side it moves in the crossflow direction from −43.02 mm at Y/H = 0.92 to 10.47 mm at Y/H = 0.5 corresponding to a deflection angle of 21.9 degrees. The downstream jet is protected from the action of the crossflow by the first jet and as a consequence it is less deflected: the center of the jet is almost coincident with the geometrical axis of the exit, and for Y/H = 0.5 it is located at X/D = +4.0 corresponding to an inclination angle of 12.3 degrees. However, considering the maximum of the mean vertical velocity component the calculated inclination angle is only 4.8 degrees which reinforces the conclusion, and the difference is probably associated with an enhanced entrainment of the second jet due to its smaller angle with the surrounding flow.
Figure 7 shows horizontal profiles of the normal stresses, ![]() and
and![]() , in a rms form, and show results that
, in a rms form, and show results that
are somewhat surprising at first sight, because it seems that it is not possible to identify completely the shear layer surrounding the impinging jets.
The peaks in the fluctuating vertical velocity components occur in the upstream side of the first jet as expected, because in this region the higher velocity gradients occur. Other peaks were observed near X = 0 for the X/H = 0.83 and 0.75 that correspond to the downstream side of the first impinging jet. For the X/H = 0.66 the peak is very weak, and for the lower profiles they cannot be pointedly identified, confirming the rapid mixing between the jets as already detected from the lower part of the flow through the vertical velocity profiles.
For the second (downstream) impinging jet the shear layer surrounding the jet cannot be clearly identified. However, for the Y/H = 0.66 profile a small decrease in the normal vertical stress is noted near the center of the jet, but the peaks around the jet are so close that the minimum value is somewhat masked.
4. Conclusions
A laser Doppler velocimeter was used to provide information on the flowfield created by twin impinging jets aligned with a low velocity crossflow. The experiments were carried out for a Reynolds number based on the jet exit conditions of Rej = 4.3 × 104, an impingement height of 20.1 jet diameters, a velocity ratio between the jet exit and the crossflow VR = Vj/Uo of 22.5, and an inter-jet spacing of S = 6D.
The results show a large penetration of the first (upstream) jet, which is deflected by the crossflow and impinges on the ground, giving rise to a ground vortex due to the collision of the radial wall and the crossflow that wraps around the impinging point like a scarf. This pattern is the usual for and impinging jet through a low velocity crossflow.
The second jet (located downstream) it is less affected by the crossflow in terms of deflection, because it is protected from the influence of the crossflow by the upstream jet. It does not reach the ground. It impinges on the wall jet that flows radially from the impinging point of the first jet.
Due to the confinement and the ground vortex, the crossflow is blocked and accelerates in the upper part and also contributes to an enhanced mixing of each secondary flow. As consequence, no upstream wall jet or ground vortex resulting from the second (downstream) jet was detected. The effect of the second jet impinging on the downstream wall jet resulting from the first jet had not been reported so far and requires further investigation.
The shear layers surrounding the jet cannot be clearly identified from the fluctuating velocities that do not exhibit clear peaks in the edges, and the values in the center are also high.
Acknowledgements
The financial support of FCT-Fundação para a Ciência e Tecnologia under contract PTDC/EME-MFE/102190/ 2008 is gratefully acknowledged.
The present work was done in the scope of the activities of LAETA-Associated Laboratory of Energy, Transports and Aeronautics.
Nomenclature
D = diameter of the jet
H = impinging height
k = turbulent kinetic energy
Re = Reynolds number
S = distance between the jets axis
U = horizontal velocity, ![]()
V = vertical velocity, ![]()
W = transverse ![]()
X = horizontal coordinate
Y = vertical coordinate
Z = transverse coordinate
Subscripts
j = jet-exit value
o = crossflow value
NOTES
*Corresponding author.