The Rotationally Symmetric Flow of Micropolar Fluids in the Presence of an Infinite Rotating Disk ()
1. Introduction
Eringen [1] introduced the theory of micropolar fluids, a sub class of microfluid [2] . The theory fully explains the internal characteristics of the substructure particles which are also allowed to undergo rotation and deformation. Airman et al. [3] concluded that the micropolar fluid serves a better model for animal blood. Guram and Smith [4] considered the flow of a micropolar fluid which is steady relative to a frame of reference rotating with small uniform angular velocity when the velocity and spin are two dimensional and depend on the depth whereas pressure is independent of the horizontal coordinates. Anwar and Guram [5] considered the flow of a micropolar fluid contained between a rotating and a stationary disk. Narayana and Rudraiah [6] discussed the flow of a viscous fluid between two disks, one rotating and the other at rest. The same problem in micropolar fluid has been studied numerically taking either suction or blowing at the stationary disk by Agrawal Dhanapal [7] .
The laminar flow due to an infinite rotating disk was first theoretically investigated with an approximate method by Von Karman [8] . Later on, Cochran [9] presented accurate numerical solutions of the Von Karman’s problem. Dolidge [10] , Sparrow & Gregg [11] and Benton [12] studied the related problems for different physical situations. Rogers and Lance [13] presented numerical solution for the flow produced by an infinite rotating disk when the fluid at infinity is in a state of solid rotation. Balaram and Luthra [14] obtained numerical solution of the steady flow produced by an infinite rotating disk when the second-order fluid at infinity is in a state of solid rotation. Sajjad et al. [15] obtained numerical solution for accelerated rotating disk in a viscous fluid. Ram and Kumar [16] analyzed three dimensional rotationally symmetric boundary layer flow of field dependent viscous fluid saturating porous medium due to the rotation of an infinite disk. Evans [17] studied the effect of uniform suction on the rotationally symmetric flow produced by an infinite rotating disc with the fluid at infinity is rotatingin the same sense as the disc.
In this research, the numerical solutions of the rotationally symmetric slow of micropolar fluids in the presence of an infinite rotating disk have been discussed. In order to find the numerical solution of the problem, the Navier Stokes equations are reduced to ordinary differential equations by using similarity transformations [17] . The finite difference scheme is solved numerically by using SOR Iterative Procedure with Simpson (1/3) Rule [18] . The calculations have been carried out using three different grid sizes to check the accuracy of the results. The numerical results have been discussed both in tabular and graphically.
The purpose of using these numerical techniques for numerical solution is that, the finite difference approximations are found to be discrete techniques wherein the domain of interest is represented by a set of points or nodes and information among these points is commonly obtained by using Taylor series expansions while the finite element method employs piecewise continuous polynomials to interpolate among nodal points. The finite difference techniques are very easy to understand and straight forward for computational analysis.
2. Mathematical Analysis
The cylindrical polar coordinates 
are used, r being the radial distance from the axis, 
, the polar angle and z the normal distance from the disk. We assume that the flow is steady and incompressible. The body force and body couples are neglected. With these assumptions the equations of motion become:
(1)
(2)
(3)
where 
is the density, 
the velocity, 
the micro-rotation or spin, p the pressure, 
is dynamic viscosity coefficient, j the micro-inertia, 
, 
, 
and k are material constants.
The following similarity transformations are used:
(4)
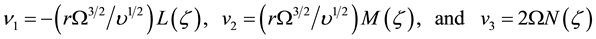
where 
is the dimensionless variable, 
being kinematics viscosity. The Equations (1) to (3) in dimensionless form become:
![]()
(5)
![]()
(6)
![]()
(7)
![]()
(8)
![]()
(9)
![]()
(10)
where primes denote differentiation with respect to![]()
. The constants C1, C2, C3, C4, C5 and C6 all are non dimensional.
The boundary conditions are
![]()
(11)
3. Finite Difference Equations
In order to obtain the numerical solution of nonlinear ordinary differential Equations (6) to (10), we approximate these equations by central difference approximation at a typical point ![]()
of the interval![]()
, we obtain
![]()
(12)
![]()
(13)
![]()
(14)
![]()
(15)
![]()
(16)
where h denotes a grid size, ![]()
and![]()
. For computational purposes, we replace the interval ![]()
by![]()
, where t is sufficiently large.
4. Computational Procedure
We now solve numerically the finite difference Equations (12) to (16) by using SOR method subject to the appropriate boundary conditions (11). The first order ordinary differential Equation (5) integrate by Simpson’s (1/3) rule subject to the initial condition ![]()
when ![]()
where a is the suction parameter.
The computation has been checked for different of the relaxation parameter between![]()
. The optimum value of the relaxation parameter for the problem under consideration is 1.5. The SOR procedure is terminated when the following condition is satisfied:
![]()
where n denotes the number of iterations and U stands for each of F, G, L, M and N. The above procedure is repeated for higher grid levels ![]()
and![]()
.
5. Discussion on Numerical Results
Numerical results have been found to observe the effect of parameters s and a on velocity field and microrotation. In order to check the accuracy of the results for velocity components F, G and H and the microrotation components L, M and N, the calculations have been carried out on three different grid sizes namely h = 0.1, 0.05 and 0.025. The three different sets of the material constants C1, C2, C3, C4, C5 and C6 in the Table 1 below have been chosen arbitrarily and calculations have been carried out for each set.
The velocity derivatives at the surface of the disc are given in Table 2 for micropolar fluids results with the results for Newtonian fluids. In Table 3 to Table 5, the numerical results are presented for s = 0.0, −0.1, −0.16 and a = 0.0, 1.5 for the material constants case I. The radial and transverse velocity components F and G are respectively depicted in Figure 1 and Figure 2 for different values of the suction parameter a when s = 0. The velocity components show a reduction in magnitude with increasing values of a. The boundary layer is clearly indicated near the surface of the disk.
Figure 3 and Figure 4 present velocity components F and G for various values of suction parameter a when s = −0.1. The figure indicates the effect of the outer flow for the first time. Some radial flow reversal is occurring in the outer flow but there is stability for the boundary layer. Thus for increasing s negatively and then the radial flow development will cause the boundary layer to leave the disk.
![]()
Table 1. Three sets of material constants used in calculations of micropolar fluids.
![]()
Table 2. The comparison of Micropolar fluids and Newtonian fluids for ![]()
and![]()
.
![]()
Figure 1. Graph of F for different values of parameter a = 0, 0.2, 0.5, 1.0 and 1.5 from top to bottom when s = 0.
![]()
Figure 2. Graphs of G for different values of parameter a = 0, 0.2, 0.5, 1.0 and 1.5 from top to bottom when s = 0.
![]()
Figure 3. Graph of F for different values of parameter a = 0, 0.3, 0.5, 1.0 and 1.5 from top to bottom when s = −0.1.
![]()
Figure 4. Graph of G for different values of parameter a = 0, 0.2, 0.5, 0.7, 1.0 and 1.5 from top to bottom when s = −0.1.
![]()
Table 3. The numerical results for velocity components F, G and H and the microrotation components L, M and N when s = 0.0 and a = 0.0.
![]()
Table 4. The numerical results for velocity components F, G and H and the microrotation components L, M and N when s = −0.01 and a = 0.0.
![]()
Table 5. The numerical results for velocity components F, G and H and the microrotation components L, M and N when s = −0.16 and a = 1.5.
![]()
Figure 5. Graph of F for different values of parameter a = 0, 0.3, 0.5 and 1.5 from top to bottom when s = −0.16.
![]()
Figure 6. Graphs of G for different values of parameter a = 0, 0.2, 0.5 and 1.5 from top to bottom when s = −0.16.
Figure 5 and Figure 6 show velocity profiles for F and G for different values of the parameter a when s = −0.16. It is noted that this value of s is limiting for which a solution for a = 0 can be found and a large value of suction is required to reduce the radial flow traversal as amount of the outflow in the boundary layer is increased. Some oscillatory behavior is seen for transverse velocity component. The flow pattern changes quickly.
NOTES
*Corresponding author.