Abstract

In this paper we shall generalize the definition given in [1] for Lipschitz condition and contractions for functions on a non-metrizable space, besides we shall give more properties of semi-linear uniform spaces.

Keywords

Lipschitz Condition, Contractions, Not Metrizable Spaces, Semi-Linear Spaces, Uniform Spaces, Fixed Point

Share and Cite:

1. Introduction

The notion of uniformity has been investigated by several mathematician as Weil [2] - [4] , Cohen [5] [6] , and Graves [7] .

The theory of uniform spaces was given by Burbaki in [8] . Also Wiels in his booklet [4] defined uniformly continuous mapping. For more information about Uniform spaces one my refer to [9] .

In 2009, Tallafha, A. and Khalil, R. [10] , defined a new type of uniform spaces, namely semi-linear uniform spaces and they gave example of semi-linear space which was not metrizable. Also they defined a set valued map on, by which they studied some cases of best approximation in such spaces. More precisely, they gave the following.

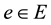Let be a semi-linear uniform space; is proximinal if for any, there exists such that. They asked that “must every compact is proximinal”, they gave the answer for the cases―i) E is finiate; ii) If converges to x, then is proximinal.

In [11] , Tallafha, A. defined another set valued map on, and gave some properties of semi-linear uniform spaces using the maps and. Also in [1] [12] , Tallafha defined Lipschitz condition and con- tractions for functions on semi-linear uniform spaces, which enabled us to study fixed point for such functions. Lipschitz condition, and contractions are usually discussed in metric and normed spaces and never been studied in other weaker spaces. We believe that the structure of semi-linear uniform spaces is very rich, and all the known results on fixed point theory can be generalized.

The object of this paper is to generalize the definition of Lipschitz condition, and contraction mapping on semi-linear uniform spaces given by Tallafha [12] . Also we shall give a new topopological properties and more properties of semi-linear uniform spaces.

2. Semi-Linear Uniform Space

Let X be a set and be a collection of subsets of, such that each element V of contains the diagonal, and for all (symmetric). is called the family of all entourages of the diagonal.

Definition 1 [10] . Let be a sub collection of, the pair is called a semi-linear uniform space if,

i) is a chain.

ii) For every, there exists such that.

iii).

iv).

Definition 2 [10] . Let be a semi-linear uniform space, for, let

. Then, the set valued map on is defined by

Clearly for all, we have and. Let

, from now on, we shall denote by.

Definition 3 [11] . Let be a semi-linear uniform space. Then, the set valued map on is

defined by,

The following results are given in [12] .

Proposition 1. Let be a semi-linear uniform space, and is a sub collection of, then, if an only if there exist such that.

Corollary 1. Let be a semi-linear uniform space. If, then,

1) There exist such that.

2).

Let the family of all entourages of the diagonal, then for all, by nV, we mean n-times and, so for all, and for all.

Proposition 2. Let be a semi-linear uniform space. If, then.

Proposition 3. Let be a semi-linear uniform space. If is a sub collection of, then

.

Question. Does?

3. Topological Properties of Semi-Linear Uniform Spaces

Definition 4 [13] . For and. The open ball of center x and radius V is defined by

, equivalently.

Clearly if, then there is a such that. So is a base for some topology on X. This topology is denoted by.

More presicly.

In [10] it is shown that is Hausdorf, so if X is finite then we have the discreet topology, therefore interest- ing examples are when X is infinite. Also, if X is infinite then should be infinite, other wise, which implies also that the topology is the discrete topology.

Proposition 4. Let be a semi-linear uniform space and a subcollection of satisfies,

i) For every, there is a such that.

ii).

iii).

Then is a semi-linear uniform space and.

Proof. Since is a subcollection of, then is a subcollection of and i), iii), iv) in definition (1.1) are satisfied. Now for ther exist such that so there is a such that So is a semi-linear uniform space. Now is clear. Let O be a nonempty open set in then if ther exist such that Let such that so hence

Theorem 1. Let be a semi-linear uniform space and the topology on X indused by, then.

i) can be consider as asubset of

ii) Fore all

Proof. i). Let, where is the interior of U with respect to the topology on

By Proposition 2.2, is a semi-linear uniform space indusing the topology on Sine we deal with the toplogy, we may replace with, so for all for some hence

ii) Is clear by definition of

In [11] , Tallafha gave some important properties of semi-linear uniform spaces, using the set valued map and.

Now we shall give more properties of semi-linear uniform spaces.

4. More Properties of Semi-Linear Uniform Spaces

Let be a semi-linear uniform space, then is a chain so there exist a well order set such that For, then, ther exist, such that. That is, there exist

such that. This implies, if then Hence

is bounded above by. By Zorn’s Lemma has a maximal element. So This copleet the proof of the following lemma.

Lemma 1. Let be a semi-linear uniform space, then where is a well order

set, then for , ther exist such that

Remember that for all the family of all entourages of the diagonal, V satisfies the following nice properties, and for all. Let and be a subcollections of, defined by and For all by Co-

rollary 1.6, there exist such that. So we can define, for an element by.

Definition 5. For and. Define by,

Clearly and for all. But need not be an element in, evin if. But we have.

Lemma 2. Let be a semi-linear uniform space, R is a well order set, and.

Then there exist, such that and if satisfied, then

Proof. For, there exist such that, so for every satisfies, we have. Hence is bounded above by. Hence be the maximal element of T.

Theorem 2. Let, and a subcolection of. For, we have

i).

ii) If satisfies, then.

iii).

iv).

v).

vi).

Proof. i). Let, then there exist such that

So there exist in such that and Since is a chain, there exist such that for all So

ii) and iv), are clear by definition of

iii) v), for all so

. Conversly, Let then, for all there exist such that So there exist in such that and

Since is a chain, there exist such that for all So

Let and replacing A by or by we have.

Corollary 2. For where is a semi-linear uniform spaces, we have,

i).

ii).

Corollary 3. Let and then

i).

ii) If satisfies then

iii).

iv).

v) If satisfies then

vi)

Also we have the follwing corollary.

Corollary 4. For where is a semi-linear uniform spaces, then.

Corollary 5. For, if then is the largest element in Γ satisfies

Also by Definition 3.6, for where is a semi-linear uniform spaces, we have,

i).

ii)

Proposition 5. Let be any distinct points in semi-linear uniform spaces. Then,

Proof. Let then, then there exist such that So there exist such that

but is a chain implies the existence of such that for all

So On the other hand by proposition 1.7,

. So for all which implies

Definition 6. For, and define

i) and the greatest common devisor of is 1.

ii).

iii).

Definition 7. Let be any points in semi-linear uniform spaces. For

, where and the greatest common devisor of is 1.

Using the a bove definition and Proposition 1.7, we have.

Proposition 6. Let and then

Proposition 7. Let be any points in semi-linear uniform spaces. If then

Definition 8. Let be an increasing sequence of positive rationals. If then

is defined by

Proposition 8. Let and an increasin sequence of positive rationals. If then

Proof. It is an immediate consequence of Proposition (7) and Definition (8).

5. Contractions

In [10] the definitions of converges and Cauchy are given. Now we shall discuss some topological properties of semi-linear uniform spaces. Since the semi-linear uniform space is a topological space then the continuity of a function is as in topology. The concept of uniform continuity is given by Wiels [4] , so we have:

Definition 9 [4] . Let, then f is uniformly continuous if such

that if then

Clearly using our notation we have:

Proposition 9. Let. Then f is uniformly continuous, if and only if such that, for all if then

The following proposition shows that we may replace by in Proposition 2.2.

Proposition 10 [12] . Let. Then f is uniformly continuous, if and only if

such that for all if then

In [10] , Tallafha gave an example of a space which was the semi-linear uniform space, but not metrizable. Till now, to define a function f that satisfies Lipschitz condition, or to be a contraction, it should be defined on a metric space to another metric space. The main idea of this paper is to define such concepts without metric spaces, and we just need a semi-linear uniform space, which is weaker as we mentioned before.

Definition 10 [1] . Let then f satisfied Lipschitz condition if there exist such

that Moreover if, then we call f a contraction.

Now we shall give a new definition of Lipschitz condition and contraction called r-Lipschitz condition and r-contraction.

Definition 11. Let then f satisfied r-Lipschitz condition if there exists such

that Moreover if then we call f a r-contraction.

Question. Let be semi-linear uniform spaces and what is the relation be- tween Lipschitz condition and r-Lipschitz condition, contraction, and r-contraction.

Remark 1 [12] . Let be semi-linear uniform spaces, then if then the topology indused by is the descrete topology which is metrizable. Therefore we can asumme that

Question [1] [12] . Let be a complete semi-linear uniform space. And be a contraction. Does f has a unique fixed point?

Question. Let be a complete semi-linear uniform space. And be r-contraction. Does f has a unique fixed point?

Conflicts of Interest

The authors declare no conflicts of interest.

References