A Micromixer Using the Taylor-Dean Flow: Effects of Aspect Ratio and Inflow Condition on the Mixing ()
1. Introduction
Recently, great attention has been paid to the development of a micro-chemical-analysis device called the micro total analysis systems (μTAS) in the field of engineering. This device, which consists of various microflow devices and sensors, functions through a series of operations such as mixture, reaction, separation, and extraction. However, the flow is in the very low Reynolds number region because of the microsize of the channel, where mechanical mixing by turbulence cannot be expected without a special artifice. Currently, a micromixer is needed to mix low-Reynolds-number flows efficiently. Stroock et al. [1] studied a micromixer generating secondary flows in a channel by carving a ditch into the channel wall surface. Sato et al. [2] made a micromixer that generates stronger secondary flows by carving ditches into the three wall surfaces of the channel. It has been shown that these methods are effective when the flow velocity is fast, although the pressure loss becomes a serious problem in this case.
On the other hand, a micromixer that uses chaos of the flow caused by a time-periodic perturbation was studied by Niu and Lee [3] and Tabeling et al. [4] . It was shown that the flow was miscible within a relatively short channel distance from the entrance compared with the mixing using only secondary flows. There also exist experimental [5] and numerical [5] [6] studies using spatially periodic boundary conditions to cause chaos. The complicated channel geometry or the device of perturbation is needed for these methods. Therefore, it is a problem that a micromixer is complicated.
Then we proposed a micromixer making use of chaos of the secondary flow, specifically, a micromixer in which the secondary flow becomes chaotic through a curved channel where two walls of the channel rotate [7] . This flow is a kind of Taylor-Dean flows [8] . Although some attempts of mixing were reported for considerably high Reynolds numbers [9] , few had been made for very low Reynolds numbers as in our study. In the present paper, we analyze the physical mechanism of chaotic mixing in the rotating curved channel flow by comparing experimental and numerical results. The secondary flow was measured by laser induced fluorescence (LIF) method to examine secondary flow characteristics. Also we performed three-dimensional numerical simulations with the open source CFD solver, OpenFOAM, for the same configuration as the experimental system to study the mechanism of chaotic mixing.
2. Experimental Setup and Procedure
The experimental setup and procedure are the same as Refs. [7] [10] . A diagram of the experimental setup is shown in Figure 1. Two working fluids (70 wt% of glycerol aqueous solution and 70 wt% of glycerol aqueous solution dissolving rhodamine B at the 2.5 ppm concentration) which are reserved in the tank ①, ② are drawn to the overflow tank ⑤, ⑥ by the pump ③, ④. Then, it flows into the curved channel, a test section ⑨, via the inlet tube ⑦ and goes to the drain tank. The test section consists of two parts, i.e., the rotor and the casing. The channel is formed of the casing and the rotor where the upper wall and right (inner) wall of the channel are the rotor walls capable of being rotated (refer to Figure 2) when one sees from the upstream of the entrance. The
![]()
Figure 1. Diagram of the experimental setup. ①, ② Tank, ③, ④ Pump, ⑤, ⑥ Overflow tank, ⑦ Inlet tube, ⑧ Motor, ⑨ Test section, ⑩ Needle valve, ⑪ Viewing block.
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 2. Enlargement of the test section (Mixer I). (a) 3-D view of the test section; (b) Top view of the test section; (c) Cross-section view of the test section.
rotor is rotated by the motor ⑧. The flux of the test section can be controlled by the needle valve ⑩ which is at the exit of the test section. We measured the number of revolutions of the rotor and the weight of outflow of working fluid during a certain time. A viewing block ⑪ is installed to ease the refraction of light in case of visualization of the secondary flow. We used Davis 8 (LaVision) for LIF.
The dimension of the curved channel is shown in Table 1. Here, 2a is the width of the curved channel, 2b the height of the curved channel, R the radius of curvature of the center line of the curved channel, and l the total length of the channel. The aspect ratio γ and the non-dimensional curvature δ are given by
 , (1)
, (1)
 . (2)
. (2)
Other non-dimensional parameters concerned are the Reynolds number Re, the Dean number De [11] and the Taylor number Tr [8] given by
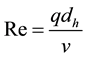 , (3)
, (3)
 , (4)
, (4)
 , (5)
, (5)
where q is the mean flow velocity in the channel axis direction,  the hydraulic diameter of the channel, ν the kinematic viscosity, and Ω the angular velocity of the rotor. If the rotation of the rotor is in the same direction as the mean flow in the channel, the parameter Ω is taken to be positive; otherwise, it is negative.
the hydraulic diameter of the channel, ν the kinematic viscosity, and Ω the angular velocity of the rotor. If the rotation of the rotor is in the same direction as the mean flow in the channel, the parameter Ω is taken to be positive; otherwise, it is negative.
Next we explain the method of visualization of the flow. A scheme of the method of visualization is shown in Figure 3. The laser sheet lights up a cross-section of the channel normal to the channel side wall and the photo- graphs of the secondary flow patterns are taken by a high speed camera. We acquired the fluorescence only of
![]()
Table 1. Dimensions of curved channel.
![]()
Figure 3. Schematic view of the method of visualization.
the rhodamine B by installing the high-pass filter (transmitted wave length of 570 nm or more) in a high speed camera for LIF to calculate the concentration distribution.
We also measured the viscosity of glycerol aqueous solution using the precision rotational viscometer before and after the experiment and confirmed that there was no viscosity change throughout the experiment. The density of glycerol aqueous solution was calculated by use of the gravimeter.
3. Numerical Simulations Methods
A numerical simulation method is the same to Ref. [10] . To examine the secondary flow characteristics in detail, we also performed three-dimensional numerical simulations for exactly the same configuration as the experimental setup. We used Open FOAM [12] for numerical simulations. The Navier-Stokes equations were solved using the icoFoam solver in which the PISO method is used for numerical calculations to obtain the flow configuration. As the inflow boundary condition, we imposed a constant axial velocity at the entrance of the channel. Constant value for the pressure and zero gradient for the velocity are imposed at the exit of the channel. After obtaining the velocity field, we solve the transport equation for the concentration using the scalar Transport Foam solver in which the SIMPLE method is used for the numerical calculation. The diffusivity is taken to be zero in the present calculation although the numerical diffusivity may be efficient in the present calculations. Two inflow conditions (refer to Figure 4) for the concentration distribution were applied at the entrance of the channel. Note that the right-hand side of each figure is the rotating inner wall.
4. Results and Discussion
Figure 5 shows experimental results of LIF under the Conditions I and II at the cross-section of 180˚ downstream from the curved channel entrance. They are results of De ≤ 0.1 Tr with the condition in which mixing was promoted as in the experiment of Condition I [7] . The right and top sides of each picture are moving walls that moves in the perpendicular direction to the sheet of the picture, while the left and bottom sides are stationary walls. The direction of the mean flow is to the other side of the sheet. The color bar on the right-hand side of the figures shows the concentration of rhodamine B. Since the concentration of rhodamine B is 100% in the half side of the entrance and 0% in the other side, it is judged that mixing is promoted if the region with intermediate concentration between 100% and 0%, specifically 50%, increases.
![]()
![]() (a) (b)
(a) (b)
Figure 4. Inflow conditions (Two fluids at the entrance. The red region is dyed by rhodamine B, whereas there is no rhodamine B in the blue region.). (a) Condition I; (b) Condition II.
![]()
Figure 5. Flow patterns of LIF at Tr = 3 and De = 0.3. (a) Mixer I; (b) Mixer II; (c) Mixer III.
In the case of Condition I of Mixer I, the region of around 50% concentration is mostly seen, where mixing is good. On the other hand, in the case of Condition II, the region of around 50% concentration becomes narrower in comparison with the result of Condition I, where mixing is not remarkable. In the case of Condition I of Mixer II, a non-mixing region is large and mixing is not remarkable. And, in the case of Condition II, the region of non-mixing becomes larger. In the case of Condition I of Mixer III, the area of good mixing region is largest among three Mixers. Thus, mixing is promoted if the aspect ratio becomes large. In addition, in the case of Condition II, a mixing region becomes narrower like other Mixers. Therefore, in this study the inflow condition that the mixing is maximally promoted is Condition I. This shows that the inflow condition is independent of the size of the interfacial area of two fluids.
Figure 6 shows the results of the numerical simulations using OpenFOAM. As the experimental results, the simulation results show the distribution of concentration in the channel cross-section 180˚ downstream from the curved channel entrance. Red color shows the region with 100% (1 when normalized) concentration, blue color shows the region with 0% (0 when normalized) concentration, and green color shows the region with 50% (0.5 when normalized) concentration. Regions of good mixing are expressed by green color.
In the case of Condition I of CFD results, mixing is promoted as the experimental (LIF) results if the aspect ratio becomes larger. In the case of Condition II, although the deformation of interfacial area of two fluids is different from the experimental results, the tendency that mixing is not promoted is the same as the experimental results. Therefore the results of experiments in the way of LIF and those of numerical simulations visualized properly agree very well, which guarantees detailed analysis of mixing process in a curved channel based on the results of numerical simulations. Thus, the discussion on the physical mechanism of mixing will be conducted using the numerical simulation results.
Using the results of the numerical simulations, the mixing rate in the cross-section at 180˚ is calculated. In order to quantitatively assess the effect of mixing, the mixture rate σ [13] defined in Equation (6) is used.
![]()
Figure 6. Flow patterns of CFD at Tr = 3 and De = 0.3. (a) Mixer I; (b) Mixer II; (c) Mixer III.
![]() (6)
(6)
In this equation ρAi is the ratio of the fluid A within the ith small region, where the region of cross section is divided into N small regions, and ![]() is as given by
is as given by
![]() , (7)
, (7)
σ = 1 when the two fluids are completely mixed, and σ = 0 when they are not mixed.
The mixing rate σ at the two conditions is plotted as De changes for three Mixers in Figure 7. Figure 7(a) and Figure 7(b) show that the mixture rate of Mixer II is small than that of Mixer I for 0 < De ≤ 1 and the difference between Conditions I and II at the inlet is small. This means that mixing process or replacing fluid particles between upper and lower parts and that between left and right parts of the channel are inactive for Mixer II. Figure 7(c) shows that the mixture rate of Mixer III is larger than that of Mixer I for 0 < De ≤ 1 if Condition I is taken as the inlet condition. This means that mixing process between left and right parts of the channel is active although mixing process between upper and lower parts of the channel is rather inactive as is illustrated by relatively small mixture rate for Condition II at the inlet.
Figure 8 shows the contour of the axial flow velocity and the streamlines of the secondary flow in case of Figure 6. In Mixer III and Mixer I where mixing is promoted, the reversal of the axial flow direction occurs. It seems that the occurrence of the axial flow reversal is caused by the pressure increase of the exit side pressure under the effect of the rotation of rotor. The secondary flow is directed toward the casing from the rotor generally, but in Mixer III and Mixer I, we notice three vortices. Figure 8(b) shows that no single vortex exists expanding from the upper wall to the lower wall, which accounts for inactiveness of mixing for Mixer II. Figure 8(c) shows that strong vortices exist between the left and right walls, which cause active mixing for Mixer III. These results mean that structure of secondary vortices play a very important role in chaotic mixing in a channel. Though in the paper by Hayamizu et al. [14] , it was shown that entanglement of path lines is important for
![]()
Figure 7. Mixing rate at Tr = 3. (a) Mixer I; (b) Mixer II; (c) Mixer III.
![]()
Figure 8. Flow velocities at Tr = 3 and De = 0.3. (a) Mixer I; (b) Mixer II; (c) Mixer III.
Lagrangian chaos in a curved channel, the present paper may add additional information of the importance of vertical structures on the enhancement of mixing.
5. Conclusion
In the present paper, we studied both experimentally and numerically the effect of varying the aspect ratio of the channel cross section on enhancement of mixing. Comparison of LIF measurements with visualization of OpenFOAM simulations exhibits very good agreement, which shows that it is possible to study mixing efficiency based on numerical simulations. It is found that for the channel elongated to the direction of the channel rotation (Mixer III), mixing is highly enhanced, for the elongated to the perpendicular direction of the rotation (Mixer II), on the other hand, mixing is rather suppressed than the case for square cross section (Mixer I). The inlet condition affects mixing efficiency a lot for Mixer III, but not for Mixer I and II. Observation of vertical structures in the channel cross section shows that mixing is strongly influenced by secondary vortices to covey fluid particles in the channel. The present results may contribute not only to μTAS designing but also to the theoretical study of chaotic mixing in a channel due to Lagrangian chaos.
Acknowledgements
One of the authors (Y. Hayamizu) expresses his cordial thanks to the Ministry of Education, Culture, Sports, Science and Technology for the financial support through the Grant-in-Aid for Scientific Research, No. 15K05814.