1. Introduction
A well-known result for a particle approaching a black hole in Schwartzschild or Kerr geometry [1] [2] is that it takes an infinite time, as measured by a clock carried by an observer in the external universe, for the particle to cross the infinite-red-shift surface given by 2GMr/ρ2 = 1. Here r is the radial distance from the center of the black hole,  , a is the rotational angular momentum of the black hole (zero in the Schwartzschild case), the angle θ is measured relative to the vertical axis of rotation, G is Newton’s gravitational constant, M is the mass of the black hole, and the light-speed c is set equal to 1. In order for a black hole to grow at a measurable rate by capturing particles of matter from the external universe, there needs to be an adjacent accretion disk [1] to aid the process. A slight possibility exists that the spherical symmetry of a Schwartzschild black hole could be sufficiently distorted, by excitation of quasi-normal modes of vibration [3] , to allow incoming particles to be captured within a finite time. For the purpose of the present note we assume that such processes are negligible.
, a is the rotational angular momentum of the black hole (zero in the Schwartzschild case), the angle θ is measured relative to the vertical axis of rotation, G is Newton’s gravitational constant, M is the mass of the black hole, and the light-speed c is set equal to 1. In order for a black hole to grow at a measurable rate by capturing particles of matter from the external universe, there needs to be an adjacent accretion disk [1] to aid the process. A slight possibility exists that the spherical symmetry of a Schwartzschild black hole could be sufficiently distorted, by excitation of quasi-normal modes of vibration [3] , to allow incoming particles to be captured within a finite time. For the purpose of the present note we assume that such processes are negligible.
The geometrical structure of a Kerr black hole of mass M and angular momentum a, as described, for example, by Padmanabhan [4] , comprises
1) A vertical symmetry axis where θ = 0 or π.
2) An outer ergosurface, given by  where a is the angular momentum and M is
where a is the angular momentum and M is
the mass of the black hole. This is a stationary limit surface, inside which it is impossible to be a stationary observer and within which the phenomenon of dragging of inertial frames occurs.
3) An outer event horizon given by . The outer event horizon and the outer ergosur-
. The outer event horizon and the outer ergosur-
face touch one another at the poles of the vertical symmetry axis. The region between these two surfaces is called either the ergosphere or the ergoregion.
4) An inner event horizon given by ,
,
5) An inner ergosurface given by , and
, and
6) A disk singularity in the plane perpendicular to the symmetry axis, given by  and z = 0.
and z = 0.
The event horizons are one-way membranes, analogous to a Schwartzschild event horizon. An incoming particle that passes through the outer event horizon must continue moving inwards until it reaches the quasi-solid core of the black hole.
The structures (2) to (6) derive from calculations rather than observations and therefore are not absolutely trustworthy, but the only serious doubt attaches to the disk singularity of item (6). This item is incompatible with the Heisenberg uncertainty principle, for the standard reason that the value of a positional variable x, y or z cannot have zero uncertainty in the physical universe without introducing an unacceptable infinite uncertainty into the conjugate momentum. The Generalized Uncertainty Principle of Vaganas and coworkers [5] -[7] provides an interesting but not yet convincing way of circumventing this difficulty. Meanwhile, the situation can be saved without doing violence to the Heisenberg principle by assuming that the predicted ring singularity is located inside the radius of the ultra-dense black hole core, so that the calculation that leads to the presence of a mathematical singularity at the center of a black hole in vacuum does not apply. In other words, the Kerr solution is a vacuum solution of Einstein’s field equation, but the core of a realistic Kerr black hole is not a vacuum.
An interesting point here is that the solution of the Einstein equation for the interior of a Kerr black hole in terms of items (2) to (6) is incomplete [4] in the sense that no known mathematical bridge exists that spans the range from a rotating neutron star which is undergoing gravitational collapse all the way to a stably rotating Kerr black hole. In the absence of such a mathematical bridge one might be driven to postulate a physical bridge, analogous to a phase change, in the form of a short-lived structure or high-energy configuration of a kind that has not yet been identified by astronomers.
In previous communications [8] [9] energy levels were calculated for neutrinos, electrons and neutrons in the gravitational potential wells of Schwartzschild black holes. It was shown that, at least in principle, a potential well could become filled with fermion neutrinos to a level above the event horizon, which would make it possible for an information-carrying flux of neutrinos to escape into the external universe. For a Kerr black hole this is true in general, not merely in principle.
2. The Growth Process
A Kerr black hole grows by capturing particles of matter inside the outer event horizon and forcibly merging them with the core. A polar on-axis approach would appear to be most effective because it reduces the likeli- hood of an incoming particle being scattered off the rotating core, but even scattered particles must eventually merge. For an off-axis incoming particle the angular momentum of the particle can either be co-rotating or coun- ter-rotating relative to rotation of the core. Padmanabhan [4] gives plots of the radius and binding energy of the innermost stable orbit prior to capture for co-rotating and counter-rotating particles that are in the accretion disk of a Kerr black hole. As would be expected, capture of a particle from a co-rotating orbit is highly favored over capture from a counter-rotating orbit.
The ultimate nature of the growth process is dependent on the depth of the gravitational potential well that has to be traversed by an incoming particle before it collides with the core. In previous communications [8] [9] the potential well depth was obtained from a solution of the Schrödinger equation for particles such as fermion neutrinos in the approximate (i.e. Newtonian) gravitational potential
 (1)
(1)
where G is Newton’s gravitational constant, M is the mass of the black hole core, and m is the neutrino mass. This gave a set of approximate energy levels as
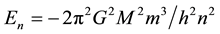 (2)
(2)
where the sum of the energy levels from n = 1 to infinity is the well depth −Ewell. One of the several approximations involved here consists of ignoring the mc2 contribution of the rest-mass of the neutrino. In practice the value of −Ewell is numerically so large (1.4 × 109 TeV for a neutrino in the gravitational well of a black hole of 106 solar masses; 1.5 × 108 TeV for the same neutrino in a black hole of 102 solar masses) that this particular approximation is valid for all likely particles. Here we are not considering the merger of two black-hole-sized objects, nor particles that arrive at the event horizon at relativistic speeds. For a very old and very large black hole the quasi-continuum of energy levels between the event horizon and the top of the potential well is available for occupation by thermally excited neutrinos and other particles that can be exchanged with the surrounding universe as part of an information flow to and from the interior of the black hole.
A particle that falls into a black hole core from the innermost stable orbit of the associated accretion disk can convey a major fraction of the energy of the well depth to the core, in addition to the kinetic energy associated with orbital motion in the accretion disk [5] . The Teravolt energies mentioned above for incoming neutrinos appear sufficient to generate a quark-gluon plasma at the site of impact of a neutrino or other particle with the core. The kinetic energy of successive particles will accumulate in the core while the relatively few scattered particles that remain temporarily outside the core become thermally distributed over the discrete energy levels in the potential well. Core temperature is assumed to be an increasing function of age. The core will be very strongly heated by the accumulation of captured particles because there is almost nowhere else for the particles’ kinetic energy to go unless one accepts, which this author does not, that anything that arrives at the center of a black hole is liable to disappear into a mathematical singularity. That hypothetical process leaves one with the unanswered question: how does a black hole ever become or remain super-massive in the presence of a mathematical singularity?
Neutrinos near the top of the thermal distribution within the well are able to escape to the external universe (Figure 1). If the energetic incoming particles are bosons rather than fermions, they too must be either added to
![]()
Figure 1. Schematic diagram of total energy (= potential energy + mass-energy + gravitational field energy + kinetic energy) minus kinetic energy for a particle, versus the distance r of the particle from the center of the black hole, for black holes of two different core temperatures.
the core or distributed over discrete energy levels inside the potential well. Therefore the extremely cold mathematical singularity that has been presumed to exist at the center of a black hole must be replaced conceptually by a quark-gluon plasma whose temperature is of the order of 1012 K or more [10] . Such plasma is both a plausible source of energetic particles in the external universe [11] and a storehouse for a large quantity of entropy [2] . The enormous depth of black holes’ gravitational potential wells, which is responsible for these remarkable heating effects, seems not to have been noticed before, except perhaps in passing (e.g. [12] [13] ).
3. Conclusion
A growing Kerr black hole has an ultra-dense, quasi-solid, spheroidal core, whose radius is greater than the radius of the theoretical ring singularity, and an associated accretion disk, whose presence is required if growth is to occur at a measurable rate. Because a black hole core is not a vacuum, the predicted ring singularity is absent. The gravitational potential wells associated with black holes are extremely deep and the kinetic energy of in- falling particles that strike the core is correspondingly large. It is proposed that bombardment of a black hole core by incoming particles of matter from the external universe can generate a quark-gluon plasma. The thermal distribution of neutrinos and other light particles over discrete energy levels in the gravitational potential well can serve as both a storehouse for entropy and a channel for transfer of information between the black hole and the external universe.
Acknowledgements
This work was supported in part by the University of Canterbury.