Abstract

As per Hawking and Bekenstein’s work on black holes, information resides on the surface and there is a limit on it amounting to a bit for every Planck area. It would seem therefore that extra dimensions would logically lead to a hyper-surface for a black hole and consequently a reduction of the corresponding information density due to the dilution effect of these additional dimensions. The present paper argues that the counterintuitive opposite of the above is what should be expected. This surprising result is a consequence of a well known theorem on measure concentration due to I. Dvoretzky.

Keywords

Higher Dimensional Black Holes, Dvoretzky’s Theorem, Information Paradox, E-Infinity Theory, Counterintuitive Geometry, Bekenstein Limit, Hawking Radiation, ‘tHooft-Susskind Black Holes

Share and Cite:

1. Introduction

It would be intuitively reasonable to suppose that in the case of black holes [1] -[10] with high dimensionality, i.e. extra dimensions [8] , the horizon i.e. the hyper quasi surface of the black hole horizon will also be of higher dimensionality. Therefore it would seem to follow that the information that resides only on the surface will be, so to speak, diluted because the Bekenstein limit is supposed to remain the same [1] [3] . In other words the net effect is that the information density will decrease or so it would seem initially [10] .

In the present short work we show that due to the well known theorem on measure concentration the above conclusion is fallacious [11] -[16] . The said theorem due to the legendary Ukrainian-Israeli mathematician and past time President of the famous Weizmann Institute, I. Dvoretzky [16] [17] leads to the definite conclusion that in sufficiently high dimensional spaces such as our quantum spacetime [12] -[14] , about 96% of the volume resides on the surface or very near to it while a near to only 4% remains in the deceptive bulk [16] [17] . An almost identical result may be obtained using E-infinity theory [11] -[14] with regard to energy where the 96% energy residing on the surface is identified with the supposedly missing so called dark energy [12] [13] . Noting the well know connection between information, entropy and thus thermodynamics and energy [2] [6] [7] we see that our conclusion has an indirect actual cosmic measurement and observational justification, in fact, confirmation [11] [12] [17] . In addition we note parenthetically that the Bekenstein wonderful result [1] -[8] upon which we are basing ourselves still needs an extension to a fractal version [11] by means of which the reduction in the information density will also be excluded [11] -[17] . It is thought that in this form the Bekenstein real limit on information will become topological and measure theoretical universality which dispels the black hole information paradox [6] [7] [11] [12] in an unheard of simplicity conserving the most important feature of the theory of Hawking on the one side and ‘tHooft-Susskind on the other without violating any fundamental laws of physics [11] [12] .

2. Analysis

In the present analysis we will follow two converging roads to show the counterintuitive results of measure concentration due to very high dimensionality. We start first by Dvoretzky’s theorem [16] [17] then we do the same using the wave-particle duality of E-infinity theory [14] .

2.1. Dvoretzky’s Theorem

The moral which we can learn, in fact relearn from this theorem is a well known wisdom from many counterintuitive results of geometry in higher dimensions, namely that we should in general never generalize an obvious conclusion from a low dimensional space to a higher one. For instance on a flat two dimensional space any two lines will intersect in a point unless they are parallel. However the spectacular failure of this simple obvious result in three dimensional space is embarrassingly clear. Now let us start with an Euclidean ball

. (1)

Working in the usual way to find the volume of this n dimensional ball we arrive via gamma function and Stirling formula to [16] [17]

. (2)

That means for V = 1 the radius is a very large one equal approximately to

. (3)

Now we proceed to the distribution of the mass, i.e. how the “volume” of this ball is distributed. To do that we estimate first the volume of a slice through the center of the unit ball. Since the radius of the ball [16] [17] is

(4)

Then the volume of the slice 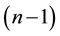dimensional ball is given by [16] [17]

. (5)

Using the Stirling formula again we find that the slice has the volume for very large n. The next question is what is the dimensional volume of a parallel slice? The slice at distance x from the center is an dimensional ball with radius so that the volume of the smaller slice is given approximately by [16] [17]

. (6)

Since r is approximately [16] [17]

(7)

one finds [16] [17]

. (8)

That means we obtain “mass” distribution that is almost Gaussian, with variance which surprisingly does not depend upon n:

. (9)

That way we conclude the following remarkable result, namely that almost all the “volume” stays within a flab of fixed width and our result announced in the introduction of the present paper follows that about 96% of the “mass”, i.e. the volume lies in the slab [16] [17]

. (10)

That means 96% is concentrated near the subspace which may be regarded as the hyper surface of an n dimensional black hole. This is a clear failure of our low dimensional intuition to anticipate what happens in high dimensional cases [16] [17] .

2.2. E-Infinity Particle-Wave Duality

In E-infinity theory the pre-quantum particle as well as the pre-quantum wave follows from the fundamental equation fixing the invariants of the noncommutative E-infinity spacetime [15]

(11)

where and. Setting a = b = 0 one finds the absolutely empty set D = 0. By contrast for a = 0 and b = 1 one finds the zero set which models the particle while its cobordism, i.e. the surface is nothing but the empty set [12] -[15]

(12)

which models the quantum wave. Transferring this result to Kaluza-Klein “quantum” spacetime we note that the “inner” volume must be correlated, i.e. intersectional which is appropriate for a volume and leads to [12] -[15]

(13)

where D (Kaluza-Klein) = 5. The outer surface, i.e. the quantum wave on the other hand is additive and non- correlated so that the union operation is what leads to the volume [12] -[15]

. (14)

A typical volume representative for both would be clearly the arithmetic mean

. (15)

In turn looking at the above as energy density we see that

(16)

for m = c = 1 while

. (17)

In other words E(O) is our familiar ordinary measurable energy density of the quantum particle [12] -[17]

(18)

while E(D) is our dark energy density of the quantum wave which we cannot measure [12] -[17]

. (19)

Adding both together we obtain the celebrated result [12] -[17]

. (20)

Now remembering that energy and information are directly related via entropy, the preceding result is confirmation of what we obtained earlier on using Dvoretzky’s theorem, namely that 96% of the information is drawn to the surface higher dimensionality rather than “diluted” by it. Needless to say, the preceding results remain valid for a rotating Kerr black hole [18] .

3. Conclusion

The mathematical literature abounds with examples demonstrating the failure of our low dimensional intuition to extrapolate from low dimensional results to higher dimensional ones [16] . The holographic boundary and the horizon of a higher dimensional black hole is no exception. Rather than diluting the density of information, a higher dimensional black hole surface has a higher information density than a lower dimensional one.

Conflicts of Interest

The authors declare no conflicts of interest.

References