Abstract

In this paper full-energy peak (photopeak) efficiency and photopeak attenuation coefficient of 3'' × 3'' NaI(Tl) well-type scintillation detector were calculated using gamma-rayisotropic radiating point sources (with photon energy: 0.245, 0.344, 0.662, 0.779, 0.964, 1.1732, 1.333 and 1.408 MeV) placed outside the detector well. These energies were obtained from ¹⁵²Eu, ¹³⁷Cs and ⁶⁰Co. The relations between the full energy peak efficiency and photopeak attenuation coefficients, were plotted vs. photon energy at different sources to detector distance, and it found that the full energy peak efficiency decreased by increasing the distance between the source and the detector.

Keywords

NaI(Tl) Well-Type Scintillation Detector, Full-Energy Peak Efficiency, Photopeak Attenuation Coefficient, Gamma-Ray Point Sources

Share and Cite:

Received 24 March 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction

In this work direct mathematical formulae for measuring the full-energy peak efficiency of HPGe well-type detector are found and the values of the measured efficiencies are compared with the published works of the experimental and theoretical old methods which have a good agreement. In this new approach the path length d(θ, ϕ) is derived as a function in the polar angle θ, and the azimuthal angle ϕ. This will reduce the mathematical formulae to an easiest and compact shape. In low level gamma-ray spectroscopy, NaI(Tl) well-type scintillation detectors are extremely useful since they offer almost 4π solid angle detection. The efficiency of such detectors can be obtained, using experimental [1] - [3] , semi-empirical [4] [5] and Monte Carlo methods [6] - [9] . The present work relies on a direct mathematical method reported by Selim and Abbas [10] - [22] , which is simple and accurate. It was used successfully in the calibration of well-type and cylindrical detectors using point, plane and volumetric sources. The efficiency is calculated in terms of the geometrical parameters of the source-detector configuration and the photopeak attenuation coefficient of the incident photon. Here, we consider 8 gamma-ray energies based on three different point sources.

2. Mathematical Treatment

In our analysis, we consider only an axial point source P, as shown in Figure 1. The efficiency in this case is given by [15]

(1)

where, d is the path length traveled by a photon through the detector active medium, μ is the attenuation coefficient of the detector material, and f_att is the attenuation factor, which is given by [17]

(2)

Here, μ_n is the attenuation coefficient of the n^th absorber for the gamma-ray photon [16] , and δ_n is the path length of the gamma-ray photon through the n^th absorber read [23] .

The polar angles, θ, are given by (see Figure 1):

(3)

(4)

(5)

(6)

The distance is the photon traveled distance (path length) inside the detector active volume. Several cases arise, let the gamma-ray photons enter from the inner bottom of the well. If they emerge from the outer bottom of the well, then is given by:

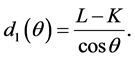(7)

But, if they emerge from the side of the outer well, reads:

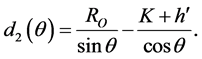(8)

Next, when the gamma-ray photons enter from the inner side of the well and emerge from the bottom of the outer well, we have

(9)

If they emerge from the side of the outer well, the photon path length is given by

(10)

Finally, when the gamma-ray photon enters from the upper surface of the well and emerge from the bottom of the outer well, then

(11)

If emerging from the side of the outer well, we have

(12)

The resulting efficiency depends on the magnitudes of the polar angles. This results in the following three cases. When θ₃ > θ₂ > θ₄ > θ₁, using Equation (1) the efficiency is given by

(13)

with

(14)

Similarly, if θ₃ > θ₂ > θ₁ > θ₄

(15)

with given by Equation (14), but j = 1, 2, 4, 6 Finally, for θ₃ > θ₄ > θ₂ > θ₁, we have

(16)

3. Results and Discussions

Using the above formalism, the full-energy peak efficiency and the photopeak attenuation coefficient of 3'' × 3'' NaI(Tl) well-type scintillation detector are calculated for in the case of point sources placed outside the detector well. The 3'' × 3'' NaI(Tl) well-type model number is 802-Canberra. The dimensions of this detector are, outer radius, 3.81 cm, cavity radius, 0.858 cm, outer height, 7.62 cm, and cavity depth, 4.987 cm. The full-energy peak efficiencies are calculated using the present work and compared with those obtained by theoretical and experimental data, for various values of the source to detector distance, h', above the detector starting approximately at 20 cm up to 50 cm in a step of 5 cm.

The results of the calculations are given in Tables 1-7, along with the experimental data and the theoretical calculations based on the transfer method presented in Ref. [23] . It is clear that our theoretical results are identical to the experimental data. The error in the theoretical results of reference [23] based on the transfer method is approximately 1%. So, our present formalism consistently produces more accurate results than the other methods.

Comparing the various data in Tables 1-7, we can see that the full-energy peak efficiency decreases as the distance h' increases for the same energy of the gamma-rays. Obviously, it can be seen that the efficiency depends on the position of the source as will as it depends on the activity of the radioactive source. In Figure 2, we summarize this point by plotting the full-energy peak efficiency versus the distance h' for the eight energies of the gamma-rays. We notice the tendency that the efficiency decreases as the energy increases for the same distance as seen in Figure 2. In addition, the efficiency curves are converging at high energies. To explain these observations, we calculate the energy dependence of the attenuation coefficient.

In our formalism, the energy of the photon only enters through the dependence of the attenuation coefficient. From Equation (14), we see that the function decreases as increases. So for the efficiency to decrease with increasing gamma energy, the attenuation coefficient should diminish. We confirm this analysis by plotting the photopeak attenuation coefficient (μ_P) against the energy of the gamma-rays in Figures 3-9 for

the different values of the distance considered so far. The figures also include polynomial fits up to 6^th order. A common trend in μ_P is that it decreases rapidly at lower energies and approximately levels of at high energies about 0.05 cm⁻¹. The sharp decrease in μ_P is reflected in the large change of the efficiency at low energies. However, the negligible variation of the attenuation coefficient with the gamma energy plays a smaller rule in determining the efficiency at high energies. Thus the efficiency curves converge as indicated in Figure 2.

4. Conclusion

The full-energy peak efficiency (ε_p) of 3'' × 3'' NaI(Tl) well-type scintillation detector, using axial point sources is calculated and compared with both the experimental and the theoretical data in Ref. [23] . In addition, the photopeak attenuation coefficients (μ_p) have been calculated as a function of the gamma-ray photon energy. Our formalism gives more accurate data than that of the transfer method presented in Ref. [23] . The dependence of the photopeak attenuation coefficient on the gamma energy is used to explain the variations in the efficiency as the distance between the point source and the detector changes. From the result it is clear that the full-energy peak efficiency ε_p decreases by increasing the distance between the detector and the source.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References