Numerical Study of Natural Convection in Square Cavity with Inner Bodies Using Finite Element Method ()
Received 28 March 2016; accepted 26 April 2016; published 29 April 2016

1. Introduction
The natural convection study in cavities with inner bodies has been of great interest nowadays due to several engineering applications. It can be useful for heat exchangers companies, electronic components cooling, heating or cooling of food products, chemical process equipment, environment control systems and others. The advance- ment in knowledge of computational in fluid dynamics (CFD) capability has contributed for more sophisticated equipment development with highest performance levels [1] .
A numerical study of natural convection inside a square cavity with inner bodies is presented in this paper. A FORTRAN algorithm code has been developed to solve the governing equations using the finite element method (FEM). The unstructured mesh developed has triangular elements and the fluid flow is laminar, two-dimensional, in transient or steady regime. FEM is chosen for this study due to its capacity in solving governing equations for complex geometries domain with efficiency and easiness of use, which is considered a great advantage of this method.
2. Problem Description
This paper aims with conjugate heat transfer study. Heat transfer by natural convection occurs in fluid air domain, Wf, and conduction in solid domain, Ws, in a square cavity with inner bodies of thermal conductivity Ks. The bottom wall is held at the uniform high temperature Th and the top wall in uniform low temperature Tc. The initial condition is assumed with fluid and bodies kept in average temperature . The dimensionless schematic of the problem is shown in Figure 1 for both cases.
. The dimensionless schematic of the problem is shown in Figure 1 for both cases.
![]() (a) (b)
(a) (b)
Figure 1. Dimensionless schematical cavities for both cases; (a) case 1 with square inner bodies, (b) case 2 with circular inner bodies.
3. Mathematical Formulation and Boundary Conditions
The finite element method is applied to solve the conservation equations for both fluid and solid domain. The air flow of this study is taken as two-dimensional, laminar, incompressible and under unsteady regime. The physical properties for fluid and solid are constant with exception of density in the body term of momentum equation for fluid and the Boussinesq approximation is invoked for fluid properties to relate density changes to temperature changes. There is not internal heat generation in the system. The governing equations for mass, momentum and energy are defined in dimensionless form. The dimensionless variables used in equations are introduced as follow:
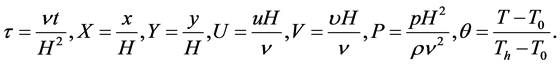 (1)
(1)
The governing equations for fluid domain are defined in dimensionless form as follow:
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
where Prandtl and Grashof numbers are defined by:
 ;
; (6)
(6)
For solid domain the energy equation is:
 (7)
(7)
where D is thermal diffusivity ratio of solid to fluid defined by:
 (8)
(8)
and thermal diffusivities are:
 ;
; (9)
(9)
The terms y, q and w are introduced in this formulation resulting in partial differential equations (PDE) valid for fluid and solid domain written as:
 (10)
(10)
 (11)
(11)
![]() (12)
(12)
Detailed mathematical procedure to achieve these PDE is described in [10] .
For Equations (10) to (12) are considered:
![]() (13)
(13)
![]() (14)
(14)
The initial and boundary conditions for Equations (10) to (12) in dimensionless form are given as:
a) For ![]()
![]() (15)
(15)
b) For ![]()
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
For Equations (16) to (21) S1, S2, S3 and S4 are surfaces of boundary in domain Ω (see Figure 1).
The average and local Nusselt number are defined by following relations, respectively:
![]() (22)
(22)
![]() (23)
(23)
where S can be S1 or S2 surface.
All the symbols and alphabetical letters used in the above equations are defined in the nomenclature chart.
4. Numerical Procedure
The numerical solution of PDE is obtained by FEM approach using Galerkin method [11] . The results of the computational code are validated by comparison with results found in literature given in Table 1. The cavity used for code validation is a standard square cavity presented in dimensional and dimensionless forms with boundary conditions shown in Figure 2.
Table 1 presents the results comparison for average Nusselt number in cold surface, Nuc, with fixed Grashof and Prandtl numbers. Table 2 presents similar comparison but with some different values for Grashof number keeping fixed Prandtl number.
![]()
Table 1. Average Nusselt number in cold surface, Nuc, for Gr = 20000 and Pr = 0.733.
![]()
Figure 2. Schematical square cavity for computational code test: (a) dimensional form, (b) dimensionless form.
![]()
Table 2. Average Nusselt number in cold surface, Nuc, for Pr = 0.733 and a number of Gr.
According with deviation values for both tables it is noted that they are higher in Table 1 but in general, the results can be considered acceptable for code validation.
Figure 3 shows the result for grid independence study for both cases 1 and 2. The average Nusselt number at cold surface for steady state, Nuc, versus grid elements number, NE, is presented. Three different non-uniform grid systems are examined for each case. Four values for Grashof number are considered (Gr = 2 × 104 to 105) and diffusivity ratio, D, and Prandtl number, Pr, are kept in 10 and 0.733 respectively.
Regarding case 1, the numbers of elements for examined grids are: 2546, 4056 and 4674. For low Grashof number 2 × 104 the average Nusselt number convergence is observed for all set of grids but for higher Grashof numbers the convergence occur for grids more refined with 4056 and 4674 elements. Considering only these two more refined grids, the maximum difference in Nusselt number values is 0.367% for all Grashof number range.
Different situation is observed for case 2, where convergence occur in practically all set of grids, independent of Grashof number. The numbers of elements for examined grids are: 1464, 2190 and 3508. In the same way, if considered only two more refined grids, the maximum difference in Nusselt number values is 0.778% for all Grashof number range.
In both cases, for the rest of calculation in this study, the non-uniform grid with 4674 and 3508 elements were chosen for case 1 and case 2, respectively, for better accuracy in the results.
5. Results and Discussion
The numerical solution was performed in transient and steady regime. The results of heat transfer by natural convection for both cases are showed in follow items. The Prandtl number is fixed in 0.733 for every numerical
![]()
Figure 3. Average Nusselt number at cold surface, Nuc, versus grid elements number, NE: (a) case 1 and (b) case 2.
solution presented in this study.
Figure 4 presents the average Nusselt number at cold surface, Nuc, versus Grashof number, Gr. The influence of parameter diffusivity ratio, D, is analyzed for four distinct values: 0.1, 1, 10 and 100. The result is presented for steady state regime and in this situation, the average Nusselt number at cold surface is equal the average Nusselt number at hot surface. For both cases is noted that for a specific Grashof number, increasing the value of D increases the average Nusselt number. For smaller values of D (0.1 and 1) the difference in average Nusselt number is more expressive than for higher values of D (10 and 100). For a fixed value of Grashof, the results have no significant variation with utilization of high values of D. Analyzing in Figure 4 the Grashof number influence for both cases, as expected, increasing Grashof number increases the average Nusselt number. The increasing in Grashof number results in higher velocities in fluid flow and more efficient heat exchange between fluid and cavity surface. Consequently, this situation improves the conductive heat transfer coefficient and increase average Nusselt number at cavity surface.
There is a good approximation in Nusselt values for case 1 and case 2, except for Gr = 5 × 104 where the difference is more notable with little advantage for case 2. These values approximation show that the difference in solid bodies geometry (square and circular) has no significant influence in final results for average Nusselt number, according with the cavity configuration (size and bodies position) and thermal parameters involved in this study.
Figure 5 presents the average Nusselt number at cold surface, Nuc, versus dimensionless time, τ. The average Nusselt number behavior with the time is presented for Grashof numbers 2 × 104, 5 × 104, 7.5 × 104 and 105 with D kept in value 10. The average Nusselt number is higher at initial dimensionless time due to high temperature gradients between fluid and cold surface. It decreases drastically in the beginning and following reach the steady regime.
In case 1, for Gr = 2 × 104 and τ > 1 the average Nusselt number tends to stabilization and steady regime. For Gr = 50 × 104 the average Nusselt number presents a stabilization in time 1 to 6, increases the value in time 6 to 8 and finally reach the steady regime. This increase observed between time 6 and 8 is due to the modification in fluid flow pattern, which presents four convective cells and change to two big ones. This situation occurs in a minor time value for higher Grashof numbers (5 × 104 and 105). This fluid flow behavior is illustrated with more detail in Figure 9 and Figure 10.
The main differences between results for case 1 and 2 in Figure 5 are: 1) case 2 presents result for average Nusselt number practically equal case 1 for Grashof number 2 × 104 but they are greater for Grashof number 5 × 104 to 105 and 2) in despite of the general behavior of average Nusselt number for case 2 is similar of case 1, the transition in fluid flow pattern from four to two convective cells occur in different values of t.
At fixed value of Grashof number equal 7.5 × 104, Figure 6 presents the average Nusselt number at cold surface, Nuc, versus dimensionless time, τ. The average Nusselt number behavior with the time is presented for diffusivity ratio values 0.1, 1, 10 and 100. For both cases 1 and 2 the curves stabilization is noted in time around 4.5, following to steady regime. It is noted that increase in D values do not represent expressive changes in behavior of average Nusselt number with time. Comparing Figure 5 and Figure 6, it is noted in steady regime that
![]()
Figure 4. Average Nusselt number at cold surface, Nuc, versus Grashof number, Gr: (a) case 1 and (b) case 2.
![]()
Figure 5. Average Nusselt number at cold surface, Nuc, versus dimensionless time, τ: (a) case 1 and (b) case 2.
![]()
Figure 6. Average Nusselt number at cold surface, Nuc, versus dimensionless time, τ: (a) case 1 and (b) case 2.
average Nusselt number is more affected by Grashof number variation than by diffusivities ratio variation.
The distribution of dimensionless temperature, q, and stream function, Y, in steady regime, is shown in Figure 7. Three values of Grashof number (2 × 104, 5 × 104 and 105) are considered and D value is fixed in 10. For low
![]()
Figure 7. Distribution of dimensionless temperature, q, and stream function, y, for case 1 in steady regime.
Grashof number 2 × 104, there are four convective cells with low values of Y, indicating that the fluid has low velocity and small recirculations, which cause small deformations in the temperature field. As can be seen, the isotherms lines are almost horizontal lines, indicating characteristic situation of pure conduction. On the other hand, for Grashof numbers 5 × 104 and 105 there are two major convective cells, with the cell situated on right side rotating in clockwise direction and the cell on left side rotating in counterclockwise direction. The higher the Grashof number, there are higher speeds and higher fluid flow recirculation resulting in greater deformation in temperature field and thus higher heat transfer hate.
For Figure 8 the considerations are the same made for Figure 7. However, it appears in case 2 greater fluid recirculation in comparison with case 1, resulting in a higher heat exchange, as evidenced by the slightly greater results of average Nusselt number for this case. This fluid recirculation is higher in case 2 due to circular geometry of inner bodies, that is more favorable for fluid recirculation between the cylinders and walls than for case 2, with square bodies.
![]()
Figure 8. Distribution of dimensionless temperature, q, and stream function, y, for case 2 in steady regime.
Different of the Figure 7 and Figure 8 where only steady regime is shown for different values of Grashof number, the Figure 9 and Figure 10 present the distribution of dimensionless temperature, q, and stream function, Y, in function of dimensionless time, τ, for case 1 and for case 2, respectively. For these analysis are considered Gr = 105 and D = 10. The main purpose of these figures is to show the evolution in time of the temperature field and the structures of fluid flow field. It is observed in these figures a stabilization of the velocity field and fluid temperature from the dimensionless time τ = 5 where steady regime is reached. For τ = 0.5 there is the formation of eight convective cells. In the time interval 0.5 to 1.2, the four cells formed between the bodies reduce their size and intensity. Following the top two cells become more intense and reduce the effects on the two cells below. In the steady regime there are pratically two predominant major cells and two small recir- culations in the cavity top.
6. Conclusions
This study numerically investigated the heat transfer problem by natural convection in a square cavity with two
![]()
Figure 9. Distribution of dimensionless temperature, q, and stream function, y, in dimensionless time, τ, for case 1.
![]()
Figure 10. Distribution of dimensionless temperature, q, and stream function, y, in dimensionless time, τ, for case 2.
inner bodies. Two cases have been studied: one of them with square inner bodies (case 1) and the other with circular inner bodies (case 2). For both cases, the bodies are solid and thermally conductive and the cavity lower and upper horizontal surfaces are isothermal with high temperature Th and Tc, respectively. Both vertical surfaces are adiabatic. A FORTRAN code using FEM is developed to solve the governing equations. The fluid is air with Prandtl number fixed in 0.733.
The results show for both cases that increasing the value of diffusivity ratio, D, increases the average Nusselt number. This difference in average Nusselt number is more expressive for variation in low values of D (0.1 to 1) than for variation in higher values of D (10 and 100).
The Grashof number has significative influence in both cases. Increasing Grashof number increases the average Nusselt number. The increasing in Grashof number results in higher velocities in fluid flow and more efficient heat exchange between fluid and cavity surface, resulting in higher average Nusselt numbers. It is noted in steady regime that average Nusselt number is more affected by Grashof number variation than by diffusivities ratio variation.
In despite of the results for average Nusselt number is near similar for both cases, it is noted that case 2 has a little advantage due its bodies with circular geometry. This circular condition is more favorable for fluid recirculation between the cylinders and walls than for fluid recirculation in case 1, with square bodies.
The distribution of dimensionless temperature, q, and stream function, Y, in function of dimensionless time, τ, are presented for both cases in this study. The parameters used are Gr = 105 and D = 10. The evolution in time of the temperature field and the structures of fluid flow field are presented. The results show that in dimensionless time τ = 5 pratically steady regime is stablished with two predominant major cells, one on cavity left side and other on right side. The cell on left presents recirculation on counterclowise direction and the cell on right side presents recirculation on clockwise direction.
Acknowledgements
The authors thank FAPEMIG for its financial support.