1. Introduction
The role of finance in economic development has been the focus of widespread discussion1. The connection between economic development and the reduction of poverty has been at the centre of a heated debate. The work of Lopez [1] identifies at least two branches of the literature which furnish a quite different response to the question of the relation between development and poverty reduction2.
On the question of the relation between finance and development it is not clear which comes first. There is most likely a wash back effect, although, according to studies by Calderon and Liu [2], the effects of financial growth on economic growth are stronger than those of the latter on the former and they are also more pronounced in developing economies than in developed ones.
Financial growth may be hampered by low interest rates which may discourage saving and thus make investments sub-optimal. The low cost of money might also encourage not very efficient investments. In this regard, McKinnon [5] and Shaw [6] have independently found that most of the state’s negative impact comes from the imposition of artificially low interest rates.
The recommendation was therefore to leave as much freedom as possible for the unfolding of economic forces. This recommendation, on the other hand, was in line with the general climate of those years, during which many scholars began to believe that state intervention in the economy was the main obstacle to achieving prosperity.
The world economy has therefore abandoned “financial repression”, and globalization has been increasingly characterized and accelerated by what is called “financialization”. The result, however, has been far beyond expectations: interest rates raised more and for longer than expected, especially in less developed countries [7]. This resulted in strangulation of small and medium-sized enterprises, which have no easy access to direct financing, and in a compression of wage levels.
There is still no common agreement about the exact meaning of the term “financialization”. Krippner [8] provides a discussion on the meaning assigned to it by various scholars who have an interest in this phenomenon:
• Growth of equity values as a form of “corporate governance”;
• Growing dominion of systems based on the financial markets rather than on “bank intermediation”;
• The increase of economic and political power of the “rentier class”;
• Explosion of financial intermediation caused by the increasing number of technical tools.
Krippner, for her part, in identifying the phenomenon underlines the growing relative importance of financial profits compared to those deriving from trade and the production of real goods.
Epstein [9] maintains that each of these definitions captures a particular aspect of the “financialization” phenomenon and adds that, in a nutshell, it is the growth of the financial institutions, markets, actors and motivations in National and International economic operations.
Also in the viewpoint of Palley [10] financialization is a process “whereby financial markets, financial institutions, and financial elites gain greater influence over economic policy and economic outcomes” [10] and therefore it is essentially an abnormal growth of finance, if compared to production activities.
In Palley’s opinion, as well as a growing importance of the financial sector over the real one, and a resulting transfer of resources for the benefit of the former, financialization has also caused an increasing inequality in income distribution and a stagnation of wages [10] and it has transformed the functioning of economic systems at both micro and macro-economic levels. At the macro level it is supposedly associated with the slowdown in growth and a greater fragility of the financial systems [10], as shown by the recurrent crises [11]. On the other hand, these crises have a less and less localized dynamic. Investments are made far from the places where the savings originate, according to a short-term logic, focused on getting quick returns. These phenomena may seem new and quite typical of our times, and this is certainly true if we look at their size and their spatial and temporal aspects, but actually they are not without historical precedent. Andriani [11] notes that the current process of globalization and financialization is not new and irreversible, because it has at least a historical precedent (of which, however, the scholar emphasizes the differences, in the period from the second half of 1929 [11]3.
2. Modelling Financialization
Before building a model to describe financialization, we must identify the essential dynamics of this phenomenon. In fact we must represent these dynamics with the utmost simplicity consistent with the need not to lose relevant information.
Andriani notes that the financialization process emanates from the real economy and then feeds back onto it [14]. The origin of development, in fact, is determined by an accumulation process. This can be started simply by saving, resulting in its turn from a surplus production or, following Schumpeter [15], by the creation on the part of the banking system, of means of payment, which become available for investment of innovative entrepreneurs who remove them from consumption.
Whichever way it began, the accumulation process, once started in an area (which we will call A), tends to expand into other areas if they are able to offer access to natural and human resources, or for selling products so as to ensure further growth of capital. We will call these expansion areas B. The greater profitability can be determined essentially by two factors: lower costs (for equal productivity) or higher revenues. The latter may result from various causes, among which, however, there is a higher productivity due to a relative abundance of some factors.
The investment in B implies an increase in local revenues, but only for the salary component, with a consequent low local saving. The savings generated may also not necessarily involve investment in B by local entrepreneurs, because the local banking system may prefer financing activities already underway, even if they are of foreign origin. All this can then make economy B into a satellite of A. Obviously this process is more likely and more rapid when the financial means allowing a relocation of investment are more flexible. In addition, the ability to quickly move capital gives landowners a greater power over employees, who are therefore forced, for the same productivity, to accept lower wages. This happens even in the country where accumulation started, thus prefiguring a polarization that is not only territorial but also functional (between the different components of the economic system).
In the following sections we will try to transfer into a mathematical model the dynamics we have just described, simplifying them as far as possible, but saving those which are essential for meaningful results to be obtained.
3. Mathematical Model
The model we are presenting at first will referred to a single closed and homogeneous economic system. We assume, for the sake of simplicity, that the only cost for entrepreneurs, besides the interest rate, is wages, and that prices are stable. Productivity, moreover, depends on the difference between the target wage T and the real wage w. T could be identified with the real wage received by workers in central areas or even with an amount considered reasonable in relation to productivity. The closer the workers’ wage is to T, the greater their effort and therefore their productivity4.
The number of workers who offer their labour will depend on the wages (in fact we can suppose that, if the wage is too low, workers will move to other regions). The equation of profit (net of interest on financing) will be:
 (3.1)
(3.1)
As a result of the arguments above, we can write the function of productivity:
 (3.2)
(3.2)
Naturally we assume w ≤ T and also α < 1 (to make the model able to exhibit decreasing marginal outputs). The first hypothesis (w ≤ T) implies that the maximum effort is produced with a wage equal to target T and that beyond this limit the effort cannot grow, because it is already at its maximum value.
If w = T, we have π = H H, then, is the maximum production of a worker in a given environment. Its value, in fact, is not unrelated to the geographical location of the firms. If the location is peripheral (i.e. if markets and/or supply sources are distant), the transport costs will reduce profits by acting on H. In fact the production will be lower if a portion of the investment is channelled into transport rather than into direct production. On the other hand H can vary from place to place, not only due to the distance (between markets or between factors), but also because of more complex reasons such as the presence (or absence) of agglomeration economies, human capital and (above all) organizational capital (not easily transferable).
Also N, the number of workers which offer their labour, as mentioned above, depends on w. For the sake of simplicity we can assume that the relation between N and w is linear:
 (3.3)
(3.3)
Inserting 3.2 and 3.3 in 3.1, we obtain:
 (3.4)
(3.4)
Equalizing to 0 the first derivative of 3.4, with respect to w, we can find the conditions which maximize profit:
 (3.5)
(3.5)
The wage which maximizes profit (which we will call w*: calculations in fn5) is:
 (3.6)
(3.6)
This wage can be, in dependence of the values of the parameters H, α, T and i (j is irrelevant) less than, equal to or greater than T. However we have assumed that the effort is maximum when w = T and therefore w* will never exceed T.
However we can easily see, by examining 3.6, that the equilibrium wage grows when productivity (expressed by H) increases, and that it is suffers a negative effect not only from the interest rate i (Figure 1 shows how an increase in i, not improbable in zones which, being depressed, have a higher risk of failures, reduces w*), but from the target wage T. This is due to the fact that a higher target, for any given wage less than w*, causes a less intense effort.
Notice, incidentally, that w* can be equal to T only if
 (3.7)6
(3.7)6
The value of H (i.e. H*) which guarantees an optimal wage (for the entrepreneurs) and allows the last to equalize the target T (we could suppose that this condition can happen in the central areas) grows, therefore, if the target T and the interest rate i increase and decrease if α grows. From 3.7 we can obtain the value of T compatible with a certain productivity H (i.e. T*, which allows equality between w* and T*):
 (3.8)
(3.8)
3.8 shows that an increase of the interest rate reduces T*, i.e. the wage to which workers can realistically aspire.
We have underlined that H in a peripheral region is usually lower than in a central area.
We could ask what happens in a similar circumstance. As we can see by examining 3.4, it is not only the equilibrium wage w*, but also the profit that decreases when H is reduced. To check what happens when two regions, a central one (which we will name A) and a peripheral (B), with HA > HB, interact, we have to compare the

Figure 1. The graph shows the relation between the interest rate i (independent variable) and the equilibrium wage w*.
marginal profits of the two regions and not the average profits7 For this purpose, then, it will be useful to use the following relation, which is the first derivative, with respect to w, of the profit:
 (3.9)
(3.9)
At this point, however, it is also necessary to distinguish at least two types of peripheral areas: those with the same target wage as the central area and those with a lower target. In fact the peripheral regions which are next to the central area8, with no geographical, political or linguistic and cultural barriers, will show, more probably than other more distant or less integrated regions, a target wage closer to the wages received by the workers of the central area.
We have already seen that a reduction of H reduces w*. We must add that in this case also the supply N, which depends on w, decreases.
Generally if HA > HB there will be a flow of capital from B to A (i.e. towards the centre) because, if TA = TB, the profits are greater in A, and this will happen with greater intensity if iA < iB.
However the opposite phenomenon is also possible, i.e. the flow of financial resources towards the peripheral areas. This will happen above all if the target of the workers in the latter areas is lower than that of the workers in the central areas (TA > TB), making them work harder for the same wage.
To make a comparison, we must use two relations as 3.9, one referring to the central area A, the other to B. In this way we will able to know the direction of investments and also to what extent they will be active:
 (3.10)
(3.10)
Due to the fact that the parameter j is irrelevant in the determination of w*, we will assume in all cases jA = jB. We will assume, moreover, the following condition (A being the central zone): HB < HA. As for interest rates, although it is reasonable to assume that they are usually but not necessarily higher in the peripheral zones, we will assume their equivalence, i.e. iA = iB, while for TB we will consider both the possible hypotheses, i.e. both TB = TA, and TB < TA. If TB is lower than TA, it is possible that lower wages are not associated to a lower effort, and this could attract investments from area A and hinder disinvestment by local firms (despite the lower value of HB).
To verify these hypotheses, it is useful to insert 3.10 into a system of differential equations:
 (3.11)9
(3.11)9
In these equations v is an investment variation coefficient. For the sake of simplicity, we can assume that it has the same value in the two areas (vA = vB = v). We assume that also φ, which measures the degree of openness of the two economic systems towards each other, has the same value in the two areas.
By observing 3.11 we can see that if the marginal profit in A is greater than in B, wages and investments will grow in A and will decrease in B, and vice versa. The second term of 3.11 in fact describes a variation in the capital invested in the respective areas which proportional to the marginal profits and also to the difference (if positive) between these marginal profits, wages and employment in the area under consideration.
Figures 2(a), (b), 3, 6, and 7 show the values of wA
 (a)
(a) (b)
(b)
Figure 2. (a) The graph shows the combinations of wA and wB which may or may not imply, for given values of the parameters (shown in the bottom of the figure), a growth of wages (and profits) in areas A and B; (b) The figure shows a detail of the graph of Figure 2(a), evidencing how, near the axis of abscissas, there are combinations of the wA and wB for which wB decreases (we have an analogous situation near the axis of ordinates, where wB grows and wA decreases).

Figure 3. The graph shows how the equilibrium wage of the area B (in E4) is lower than in Figure 1, in dependence of a higher value of TB (1000 instead of 900).
and wB, whether or not they are associated to a growth in the respective areas, ceteris paribus, for different values of φ, TA, TB. The equilibrium points are E1, E2, E3 and E4. The first is a trivial point, because it entails the absence of investments and economic activities in both regions, E2 entails the absence of investments in area B, E3 the absence of investments in area A. E4 is the only stable equilibrium point, implying an effective equilibrium between the two regions, and therefore we will concentrate on it.
The coordinates of E4 are the following10:
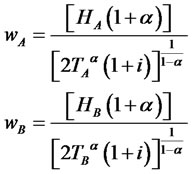 (3.12)
(3.12)
We have already shown when examining 3.6 that the growth of T reduces the equilibrium wage. Therefore, if TB is related to the wage of the central area (A), since we can assume that the latter is incompatible with the productivity of the peripheral area for the purpose of profit maximization, the equilibrium wage of the peripheral zone will decrease (see Figure 3). This is confirmed by the numerical simulations of Figures 4 and 5, in which the sole parameter that changes value is, precisely, TB (900 in the simulation of Figure 4, 1000 in the simulation Figure 5): the final wage wB in the second case is far lower.
The growth of φ, on the other hand, does not affect the final equilibrium. Figure 6, in fact, shows that, even when sets of values of wA and wB associated to their growth are changed, E4 does not change. However the area of combinations of wA and wB which cause a growth of both the variables ( and
and ) decreases.
) decreases.
Generally, however, high values of φ (which imply a great sensitivity of investments to the difference in profitability between the two areas) cause a delay in reaching the equilibrium. In addition, if the value of wA is quite a bit higher than the value of wB (showing a significant difference between the development of the two areas), before moving towards the final equilibrium value it can greatly decrease (see Figure 6: evolutionary trajectories in the zone ,
, ).
).
Figure 7 shows a situation in which the propensity to relocation is very high (φ = 11): the area of combinations of wA and wB which cause both of them to grow is divided into two zones separated by the combinations which bring about the growth of wA alone. This is indicative of the fact that if two economic systems, with dif-