2021 年 99 巻 2 号 p. 537-554
2021 年 99 巻 2 号 p. 537-554
This study examines the role of boundary layer dynamics in tropical cyclone (TC) intensification using numerical simulations. The hypothesis is that although surface friction has a negative effect on TC intensification due to frictional dissipation (direct effect), it contributes positively to TC intensification by determining the amplitude and radial location of eyewall updrafts/convection (indirect effect). Results from a boundary layer model indicate that TCs with a larger surface drag coefficient (CD) can induce stronger and more inwardly penetrated boundary layer inflow and upward motion at the top of the boundary layer. This can lead to stronger and more inwardly located condensational heating inside the radius of maximum wind with higher inertial stability and is favorable for more rapid intensification.
Results from full-physics model simulations using TC Model version 4 (TCM4) demonstrate that the intensification rate of a TC during the primary intensification stage is insensitive to CD if CD is changed over a reasonable range. This is because the increased/reduced positive contribution by the indirect effect of surface friction to TC intensification due to increased/reduced CD is roughly offset by the increased/reduced negative (direct) dissipation effect due to surface friction. However, greater surface friction can significantly shorten the initial spinup period through stronger frictional moisture convergence and Ekman pumping and thus expedite moistening of the innercore column of the TC vortex but is likely to lead to a weaker storm in the mature stage.
Tropical cyclone (TC) intensification has been extensively studied in the literature. Observations indicate that TCs tend to develop and intensify over the ocean with high enthalpy flux potential, rich moisture, and high conditional instability in the mid–lower troposphere (Riehl 1950; Malkus and Riehl 1960; Gray 1968). The energy transferred from the ocean to the atmosphere, in terms of surface enthalpy flux, largely determines the development and maximum intensity of a TC (e.g., Malkus and Riehl 1960; Emanuel 1995, 1997). Because the boundary layer is the medium that communicates between the free atmosphere above and the ocean below, the boundary layer dynamics in the presence of surface friction are recognized as being important for TC intensification, but their actual role has not been fully understood (Smith et al. 2009; Stern et al. 2015; Heng and Wang 2016a, b; Smith and Montgomery 2016; Heng et al. 2017; Kepert 2017; Kilroy et al. 2017; Heng et al. 2018; Montgomery and Smith 2018).
Most previous studies (Craig and Gray 1996; Persing et al. 2013; Thomsen et al. 2012; Peng et al. 2018) demonstrated that the intensification rate of a TC simulated in state-of-the-art high-resolution numerical models is often insensitive to surface drag coefficient (CD) or surface friction. Craig and Gray (1996) argued that this insensitivity implied the unimportance of the convective instability of the second kind (CISK, Charney and Eliassen 1964) to TC intensification. The CISK theory describes a positive feedback between cumulus convection in the TC core and frictionally induced boundary layer moisture convergence and Ekman pumping. This seems to imply that the positive feedback in CISK should be enhanced with a larger CD; this is not true in model simulations, as noted by Craig and Gray (1996). In a more recent study, Montgomery et al. (2010) examined the sensitivity of the intensification rate of a simulated TC to CD using a three-dimensional, nonhydrostatic, cloud-resolving model. They demonstrated that the intensification rate and mature intensity of the simulated TC increased slightly with an increase in CD when CD was less than 2.0 × 10−3, but only the mature intensity decreased for a larger CD. By contrast, the storm without surface friction (CD = 0) does not intensify in their simulation. In a follow-up modeling study, Thomsen et al. (2012) demonstrated that the simulated TC intensification rate and mature intensity were both insensitive to randomly perturbed CD with changes as large as 60 %. Therefore, based on previous studies, surface friction is indispensable to the formation and intensification of a TC and limits its mature intensity. The intensification rate of a TC during its primary intensification stage (namely, after the initial spinup period) is insensitive to the surface drag coefficient in a reasonable range, which is in the order of 10−3 based on the observed estimation. However, such insensitivity is still not well understood.
Previous studies based on balanced vortex dynamics demonstrate that the intensification rate of a TC is largely controlled by both the amplitude and radial location of condensational heating in the eyewall (Schubert and Hack 1982; Shapiro and Willoughby 1982; Nolan et al. 2007; Vigh and Schubert 2009; Pendergrass and Willoughby 2009). These studies indicate that TCs with condensational heating (convection) inside the radius of maximum wind (RMW), where inertial stability is high, intensify more rapidly. Pendergrass and Willoughby (2009) found that the intensification rate of a TC vortex also depends on the storm structure in addition to the radial location of condensational heating. The dependence of the TC intensification rate on the storm structure was examined based on composite aircraft data by Rogers et al. (2013), who found that the intensifying TCs had a more rapid radial decay rate of tangential wind outside the RMW and had more convective bursts inside the RMW. Recently, Zhang et al. (2017) and Zhang and Rogers (2019) also suggested that the boundary layer inflow and eyewall convection would be stronger if reduced vertical eddy diffusivity was used, leading to an improved TC intensification forecast. These studies thus suggest that the radial location and amplitude of eyewall convection and the radial profile of tangential wind outside the RMW are essential to TC intensification. However, currently, there is limited knowledge of what determines the radial location of eyewall convection and how the vortex structure plays an important role in determining the amplitude, radial location of eyewall convection and, thus, condensational heating.
Eyewall convection in a TC is always rooted in the frictional boundary layer, where mass and moisture convergence and large surface enthalpy flux are located. In most early successful numerical simulations of TCs, moist convection was often parameterized based on mass flux (vertical motion) at the top of the boundary layer (e.g., Ooyama 1969; Yamasaki 1968; DeMaria and Schubert 1984). Based on results from a revised version of Ooyama's three-layer model, Frisius and Lee (2016) found that the TC intensified less rapidly in the simulation with a balanced boundary layer than in the simulation with an unbalanced boundary layer. They demonstrated that the faster intensification with the unbalanced boundary layer resulted from the more inwardly penetrated boundary layer inflow, which leads to the eyewall convective ring well inside the RMW. This indicates the importance of the unbalanced boundary layer dynamics to the radial location of eyewall convection. More recently, Kepert (2017) studied the boundary layer's influence on the radial location of frictional eyewall updraft (and thus convection) and demonstrated that the frictional eyewall updraft is typically displaced toward the inside of the RMW. This inward displacement of the eyewall updraft relative to the RMW favors eyewall contraction, particularly when the RMW is relatively large. Kepert (2017) found that the inward displacement of the frictional eyewall updraft relative to the RMW is positively proportional to the boundary layer inflow and inversely proportional to the inner-core inertial stability. As for a given TC intensity and structure, greater surface friction (CD), as well as smaller vertical diffusivity, can produce stronger boundary layer inflow, larger CD may favor a stronger and more inwardly displaced eyewall updraft and, thus, a more rapid TC intensification. These studies demonstrated the positive role of boundary layer dynamics in controlling the organization of eyewall convection and condensational heating in the eyewall and, thus, the intensification of a TC.
However, surface friction also acts as a sink of kinetic energy and should thus dynamically have an overall negative effect on TC intensity and intensification (Stern et al. 2015; Heng and Wang 2016a; Heng et al. 2017, 2018). Note that although some studies consider that the development of supergradient wind in the boundary layer could contribute to the spinup of the eyewall of a TC (Smith and Montgomery 2015; Montgomery and Smith 2017), other studies demonstrate insignificant contributions of the upward advection of supergradient component of tangential wind in the boundary layer to the spinup of the eyewall above the boundary layer (Li et al. 2020; Fei et al. 2021). Nevertheless, one can consider that surface friction has two opposing effects on TC intensification. On the one hand, surface friction can reduce kinetic energy of the TC system through the frictional dissipation effect (direct effect). On the other hand, it may lead to stronger and more inwardly displaced eyewall updraft and convection, contributing positively to TC intensification (indirect effect). Contrary to the direct frictional dissipation effect, we use “indirect effect” to represent the boundary layer's dynamical controls on eyewall condensational heating. Ooyama (1969) did an energy budget for a TC lifetime in his three-layer model and found that the net gain from potential energy to kinetic energy (condensational heating) was greater than the net loss of kinetic energy to the ocean (frictional dissipation effect) in the TC inner core during the intensification stage and became nearly balanced by the net energy loss due to surface friction when the TC entered its mature stage. These results provided insights into the energetics in the lifetime of a TC. It is our hypothesis that in a reasonable parameter space, changes in the positive indirect effect and negative direct frictional dissipation effect due to change in CD often largely offset each other, giving rise to the insensitivity of the simulated TC intensification rate to change in CD.
The purpose of this study is to verify our aforementioned hypothesis, understand the role of boundary layer dynamics in TC intensification, and examine how the TC structure affects the TC intensification rate through boundary layer dynamics. In Part I, both a boundary layer model and a full-physics model are used to perform a series of sensitivity experiments to help understand why the simulated TC intensification rate is insensitive to CD. In Part II, the sensitivity of TC intensification to the initial TC vortex structure will be understood based on the dependence of the frictional eyewall updraft on the TC structure. The rest of the paper is organized as follows. A brief description of the models used and the experimental design are given in Section 2. Results from the boundary layer model are briefly discussed in Section 3 to demonstrate how the frictional eyewall updraft in the steady-state response depends on CD. Results from the sensitivity experiments using a full-physics model are discussed in Section 4 to help understand why the simulated TC intensification rate is insensitive to change in CD. Our main conclusions are provided in Section 5.
The multi-level axisymmetric TC boundary layer model used in this study is a simplified version of the TC boundary layer model of Kepert and Wang (2001) and is similar to that used in Kepert (2017). The model includes two momentum equations and a mass continuity equation as follows:
 |
 |
 |
 , where vp is the gradient (tangential) wind above the boundary layer. Fu and Fv are the vertical diffusion terms of u and v; and Du and Dv are the horizontal diffusions of u and v, respectively, all calculated following Rotunno and Emanuel (1987), except for a constant Brunt-Väisälä frequency N of 10−3 s−1, namely a very weakly stable boundary layer. The surface drag coefficient is given as
, where vp is the gradient (tangential) wind above the boundary layer. Fu and Fv are the vertical diffusion terms of u and v; and Du and Dv are the horizontal diffusions of u and v, respectively, all calculated following Rotunno and Emanuel (1987), except for a constant Brunt-Väisälä frequency N of 10−3 s−1, namely a very weakly stable boundary layer. The surface drag coefficient is given as
 |
The modified parametric TC tangential wind profile (Wood and White 2011; Wood et al. 2013) is used to define the gradient wind at the model top, namely
 |
 |
To understand the effect of surface friction on the steady-state response of the boundary layer flow to a specified gradient wind distribution at the model top, the sensitivity experiments to CD were conducted by multiplying the default value of CD in equation (1) by a factor from 0.5 to 2, with an interval of 0.05 (31 cases in total). In Part I, because we focused on the sensitivity to CD, only one set of parameters were used for the TC vortex with Vm = 15 m s−1, Rm = 40 km, and b = 1.0. Note that given a time-independent radial distribution of tangential (gradient) wind at the model top, the boundary layer response achieves a steady state after several hours of the model integration (not presented). In this regard, the boundary layer response can be considered a fast adjustment process compared to the lifecycle of a TC. All boundary layer model experiments were integrated for 12 hours when a steady state was reached. Note that surface friction does not affect the radial distribution of gradient wind at the model top in all boundary layer model experiments.
2.2 Tropical Cyclone Model (version 4)TC Model version 4 (TCM4) developed by Wang (2007) was used in this study, which is a quadruply nested, fully compressible, and nonhydrostatic primitive equation model. The lower boundary is a flat surface with unperturbed surface pressure of 1,010 hPa. The upper boundary is set at an approximately 38 km height, with a sponge-type layer above an approximately 20 km height to absorb the upward-propagating gravity and sound waves, as in Durran and Klemp (1983). The model domain has four two-way, interactively nested meshes, with horizontal grid spacings of 67.5, 22.5, 7.5, and 2.5 km and domain sizes of 281 × 241, 181 × 181, 217 × 217, and 271 × 271 grid points, respectively. The model has 32 vertical levels with relatively higher resolutions in the boundary layer and near the tropopause.
The model physics includes a modified Monin-Obukhov scheme for surface flux calculation (Fairall et al. 2003); an E-ε turbulence closure scheme for subgrid-scale vertical turbulent mixing (Langland and Liou 1996), an explicit treatment of mixed-phase bulk cloud microphysics (Wang 1999, 2001); a Newtonian cooling term that is added to the potential temperature equation to mimic long-wave radiative cooling used by Rotunno and Emanuel (1987); a nonlinear fourth-order horizontal diffusion term with the deformation-dependent diffusion coefficient for all prognostic variables, except for that related to the mass conservation equation; and dissipative heating due to the turbulent kinetic energy dissipation ε added to the thermodynamic equation. Cumulus parameterization was not employed even in the outermost domain, because in an environment at rest, convection and spiral rainbands are mainly active within a radius of around 300 km from the TC center and are thus covered by the innermost mesh. A more complete description and application of TCM4 to TC studies can be found elsewhere (e.g., Wang 2007, 2008a, b, 2009; Wang and Xu 2010; Xu and Wang 2010a, b; Li and Wang 2012; Li et al. 2015; Wang and Heng 2016; Heng and Wang 2016a; Heng et al. 2017).
The model was initialized with an idealized axisymmetric cyclonic vortex, which has a radial tangential wind distribution at the surface given below:
 |
In TCM4, the surface stress is calculated based on surface drag coefficient, which can be fitted as a function of 10 m wind speed as given below.
 |
Table 1 lists the numerical experiments conducted using TCM4. In the control experiment (CTRL), the initial vortex had the maximum tangential wind speed Vm = 15.0 m s−1 at Rm = 75 km with b = 1.0. In the sensitivity experiments to CD (CT05 and CT20), the default value used in CTRL in (4) was multiplied by a factor of 50 % and 200 %, respectively. To exclude the impact of CD on the initial spinup period of the TC prior to the primary intensification stage, experiments CT05 and CT20 were repeated but with CD multiplied by, respectively, 50 % (CT05R) and 200 % (CT20R) after a 36 h spinup in CTRL.

To understand the effects of the dependence of CD on surface wind speed, a new surface wind speed-dependent CD modeled with a 50 km fetch by Donelan (2018) was fitted and given as follows.
 |
 |
Figure 1 presents the four surface wind speed-dependent CD values calculated using Eqs. (1), (4), (5), and (6). In experiments CTDO and CTD1, the surface wind speed-dependent CD values given in (5) and (6) were used to replace the CD used in CTRL (4) to examine the effect of different surface wind speed-dependent CDs on TC intensification. All full-physics model experiments were integrated for 180 h, but the following analyses will focus on the initial spinup stage and the subsequent primary intensification stage (see the definition in Section 4a). Here, the initial spinup stage refers to the initial period prior to the primary intensification stage.

The dependence of surface drag coefficients (10−3) on 10-m height wind speed (m s−1) used in the boundary layer model (red), used as default in TCM4 (black), used in Donelan (2018) (CTDO, magenta), and used as modified Donelan (CTD1, blue).
The dependence of the steady-state response of the boundary layer to the prescribed radial distribution of gradient wind at the model top on CD was examined using the boundary layer model described in Section 2.1. Figure 2 illustrates the radius-height cross-sections of the steady-state response of both tangential and radial winds and vertical relative vorticity and vertical motion at different CD values. We can see from Fig. 2 that the boundary layer inflow is stronger and deeper, and the upward motion is stronger and located more inward with a larger CD. The stronger and more inwardly penetrated inflow may contribute to the contraction of the RMW and the stronger and more inwardly displaced vorticity ring and frictional eyewall updraft. These features favor eyewall convection to occur more inside the RMW with higher inertial stability and could thus contribute positively to TC intensification (indirect effect of surface friction), as inferred from the balanced dynamics (Schubert and Hack 1982; Vigh and Schubert 2009).

Radius-height cross-sections of (a, c, e) tangential (shaded; m s−1) and radial wind speeds (contours; m s−1) and (b, d, f) vertical vorticity (shaded; 10−4 s−1) and vertical velocity (contours; with contour interval of 2 m s−1) for (a, b) 100 % CD, (c, d) 50 % CD, and (e, f) 200 % CD in the steady-state response in the boundary layer model.
To give an overall description of the dependence of the boundary layer response on CD, Fig. 3a presents the minimum radial wind (maximum inflow) and the maximum vertical motion at the top of the inflow boundary layer from all sensitivity experiments with the boundary layer model. The figure indicates that a storm with a larger CD corresponds to stronger boundary layer inflow along with stronger upward motion at the top of the inflow boundary layer. A larger CD can also induce stronger and more inwardly displaced frictional updraft inside the RMW (Fig. 3b) and would be favorable for more rapid intensification if only the indirect effect of surface friction is considered. Note that the effect of increasing CD on both maximum vertical motion and updraft location relative to the RMW decreases when CD is larger, implying that the indirect effect may be saturated at some point because there is little room for further penetration of the frictional inflow. Also note that because the gradient wind distribution at the model top was prescribed and independent of time, the maximum gradient wind speed (i.e., storm intensity) was not affected by the frictional dissipation effect of surface friction in the boundary layer model experiments. However, these results from the boundary layer model imply possible positive indirect effect of surface friction on TC intensification. This is further demonstrated and compared with results from the full-physics model TCM4 in the next section.

Dependence of (a) the maximum radial wind (inflow) speed (solid, left ordinate, m s−1) and the maximum vertical velocity (dashed, right ordinate, m s−1) and (b) the inward displacement (km) of the frictional eyewall updraft relative to the RMW near the top of the boundary layer (at the 866 m height) on multiples of the surface drag coefficient in the steady-state response in the boundary layer model.
Figure 4 illustrates the time evolution of the maximum 10-m height azimuthal mean tangential wind speed and the corresponding intensification rate with different CD values from the beginning of all simulations. In our discussion, we divide the storm intensity evolution into three different stages: the initial spinup stage, the primary intensification stage, and the quasisteady stage. The initial spinup stage is defined as the period from the initial time to the time when the storm intensity (maximum 10-m height tangential wind speed) becomes higher than its average intensity during the past 12 h of the simulation. The primary intensification stage is defined from the end of the initial spinup stage to the time when the storm intensity is no longer higher than the average intensity in the past 12 h of simulation. The last stage, the quasi-steady stage or mature stage, is defined as the time period from the end of the primary intensification stage to the end of the model simulation. In CTRL, the TC experienced an initial spinup stage for approximately 24 h and then intensified until approximately 120 h. This was followed by a quasi-steady stage until the end of the 180 h simulation (Fig. 4a), with a maximum 10-m height wind speed of around 75 m s−1 at an RMW of around 15–20 km. The period 24–120 h of the simulation was the primary intensification stage of the simulated TC in CTRL.

Time evolution of (a) the maximum azimuthal mean 10-m height tangential wind speed (m s−1) with a 5 h running mean in the control experiment (CTRL, black), 50 % CD experiment (CT05, blue), and 200 % CD experiment (CT20, red), and (b) the 24 h intensification rates [m s−1 (24 h)−1] with a 5 h running mean in CT05 (blue), CTRL (black), and CT20 (red).
From Fig. 4a, we can see that the storm with larger CD (CT20) intensified 12 h earlier than the storm with smaller CD (CT05). The initial spinup stage was shorter in the former (approximately 24 h) than in the latter (approximately 36 h). By contrast, the overall intensity during the quasi-steady stage was weaker with a larger CD than that during the quasi-steady with a smaller CD. This is consistent with the theoretical maximum potential intensity (MPI), which predicts an MPI inversely proportional to the square root of CD (Emanuel 1988, 1989). However, the simulated storms with different CD values had similar intensification rates during their corresponding primary intensification stage (Fig. 4b). For example, the 24 h intensification rates of the storms in CT05, CTRL, and CT20 were all around 20 m s−1 (24 h)−1 before 72 h of the simulations. The intensification rate in CT20 decreased after reaching a maximum, while a high intensification rate remained in other experiments even after 48 h of the simulations. This is mainly because the storm with a larger CD in CT20 had the lowest quasi-steady intensity and reached its quasi-steady stage earlier than storms in other experiments because it intensified at a similar intensification rate. This led to the shortest primary intensification stage for the storm in CT20.
The duration of the initial spinup stage in the simulated storm is closely related to the initial moistening and saturation of the inner core, which is accomplished predominantly by moisture convergence in the boundary layer and Ekman pumping associated with surface friction and vertical mixing (Xu and Wang 2018). This can be clearly seen in Fig. 5, which indicates the radius-time cross-sections of relative humidity near the top of the boundary layer for the storms in CT05 and CT20. Comparing Fig. 5a with Fig. 5b, we can see that the boundary layer was more rapidly moistened in CT20 than in CT05, indicating that a larger CD favored greater moisture convergence and stronger Ekman pumping and moistening of the inner core of the storm in the simulation. Greater Ekman pumping in response to a larger CD (and surface friction) can transport more moisture from the boundary layer upward to moisten the inner-core column of the TC, leading to an earlier saturation and initiation of convection in the inner core and the onset of the primary intensification stage. This suggests that boundary layer dynamics are key to the initial moistening and initiation of convection in the inner core of the TC vortex, which would shorten the initial spinup stage of the simulated storm. Note that the storm started to intensify after the averaged relative humidity at the top of the boundary layer within the RMW reached approximately 90 % in both CT05 and CT20 (Fig. 5c). The onset time of the primary intensification stage for the storm with smaller CD was considerably delayed. This is consistent with the results of Kilroy et al. (2017), who demonstrated that surface friction plays a key role in organizing deep convection in the inner core and shortening the initial spinup stage compared to an experiment without surface friction.

Radius-time cross-sections of the azimuthal mean relative humidity (%) at the 1,331 m height in (a) CT05 and (b) CT20. The black dots represent the RMW at the same height. (c) Time evolution of relative humidity (%) with a 5 h running mean at the 1,331 m height averaged within the RMW in CT05 (blue) and CT20 (red). The blue (red) dashed line denotes the time when the storm starts its primary intensification stage in CT05 (CT20).
To isolate the impact of CD on the primary intensification stage from that on the initial spinup stage, CT05R and CT20R were conducted with CD multiplied by 0.5 and 2.0 after the initial 36 h spinup in CTRL. Figure 6 compares the evolution of the simulated storm intensities and intensification rates in CT05R, CT20R, and CTRL. We can see that the intensification rates during the primary intensification stage were very close to each other in the three experiments, confirming that the TC intensification rate during the primary intensification stage is insensitive to CD. Because the storm in CT20R approached its quasi-steady stage after approximately 60 h of simulation (Fig. 6a), the intensification rate decreased afterwards (Fig. 6b). The storm in CT05R was still in its primary intensification stage after 60 h of simulation (Fig. 6a). Correspondingly, the intensification rate in CT05R indicated an increase between 54 h and 72 h (Fig. 6b). Note that the storm intensity in the quasi-steady stage in CT05R and CT20R was very similar to that in experiments CT05 and CT20 (cf. Fig. 4a). This implies that the quasi-steady intensity is independent of the duration of the initial spinup stage of the simulated storm.

(a) Time evolution of the maximum azimuthal mean 10-m height tangential wind speed (m s−1) with a 5 h running mean in CTRL (black), 50 % CD, and 200 % CD experiments with CD changed after 36 h spinup in CTRL (CT05R, dashed blue; CT20R, dashed red). (b) Time evolution of the 24 h intensification rate [m s−1 (24 h)−1] with a 5 h running mean in CTRL (black), CT05R (dashed blue), and CT20R (dashed red).
The aforementioned results demonstrate that the increased surface friction due to an increase in CD shortens durations of the initial spinup stage and the primary intensification stage and reduces the quasisteady TC intensity but has little effect on the intensification rate during the primary intensification stage. In addition, we note that although the intensification rates in CT05R and CT20R were similar during the primary intensification stage, the storm's inner-core size in CT05R was larger due to relatively weaker contraction associated with the reduced surface friction than in CT20R (not presented).
4.2 Direct and indirect effects of surface frictionOne of the main objectives of this study is to understand why the simulated TC intensification rate during the primary intensification stage is insensitive to CD. As mentioned in the introduction, it is our hypothesis that this insensitivity results mainly from an offset of changes in the negative dissipation effect and the positive indirect effect of surface friction on TC intensification. Results from the boundary layer model in Section 3 suggest that greater surface friction may enhance the indirect effect of surface friction on TC intensification by enhancing the amplitude of the inwardly displaced eyewall updraft and condensational heating inside the RMW in the region with higher inertial stability. However, because the radial distribution of gradient wind at the model top is prescribed, results from the boundary layer model discussed in Section 3 are the steady-state response and thus only provide some implications to the possible indirect effect of surface friction on TC intensification. Therefore, here we must examine both the indirect effect and the direct dissipation effect of surface friction in the full-physics model simulations.
Figure 7 illustrates the radius-height cross-sections of the azimuthal mean radial wind, vertical velocity, and the condensational heating rate averaged in the 3 h period between 37 h and 40 h of the simulations, shortly after the change in CD, in experiments CT05R and CT20R. The azimuthal mean boundary layer inflow was stronger in CT20R than in CT05R, and the associated vertical motion was stronger and penetrated more inward in CT20R (with the maximum at a radius of around 25 km) than in CT05R (with the maximum at a radius of around 50 km) (Figs. 7a, b). As a result, the azimuthal mean condensational heating rate also became higher and was located more inward in CT20R than in CT05R (Figs. 7c, d). Similar behaviors are illustrated in Figs. 7e and 7f, which come from two additional experiments using the boundary layer model forced by the azimuthal mean pressure gradient force in the boundary layer, averaged between 37 h and 40 h. In experiments CT05R and CT20R using TCM4, we can see that the overall structure and the differences among the experiments are quite similar to those directly from TCM4 (Figs. 7a, b). These results are generally consistent with those implied from the boundary layer model discussed in Section 3, which suggest that larger CD can induce stronger and more inwardly penetrated boundary layer inflow and stronger and more inwardly displaced eyewall updraft and condensational heating through the boundary layer dynamics. Note that although the surface wind dependences of CD and tangential wind profile are different between the boundary layer model and TCM4 (cf. Fig. 1), the boundary layer responses are quite consistent. Also note that whereas considerable differences in the condensational heating rate in the inner-core region occurred shortly after CD was changed, radial wind above the boundary layer indicates little difference between experiments CT05R and CT20R (Figs. 7a, b), suggesting that the response of the transverse circulation above the boundary layer to changes in condensational heating in the eyewall is slower than the response of the boundary layer to surface friction.

Radius-height cross-sections of (a, b) the azimuthal mean radial wind speed (shading, m s−1) and vertical velocity (contours, m s−1) and (c, d) condensational heating rate (shading, K h−1) and inertial stability (contours, 10−4 s−1) for CT05R (a, c) and CT20R (b, d) from 36 h of simulation in CTRL after CD was modified in the two experiments; all variables are averaged between 37 h and 40 h of simulations. The red solid curve shows the RMW in the corresponding experiments. (e, f) Radius-height cross-sections of radial wind speed (shading, m s−1) and vertical velocity (contours, with contour interval of 0.1 m s−1) for (e) CT05R and (f) CT20R in the steady-state response in the boundary layer model to the azimuthal radial gradient wind distribution averaged between 37 h and 40 h of full-physics TCM4 simulations.
Previous studies suggest that stronger and more inwardly displaced condensational heating could favor a higher intensification rate of the TC (Schubert and Hack 1982; Vigh and Schubert 2009). However, the simulated storm in the full-physics model indicated similar intensification rates in CT20R and CT05R, although CD differed by a factor of 4. This is mainly because larger CD imposed a larger dissipation effect on the simulated storm in the full-physics model. This is different from that in the boundary-layer model experiments, where surface friction did not affect the maximum gradient wind speed because the gradient wind was prescribed and time-independent in the boundary layer model. This means that the increased positive contribution by the indirect effect of surface friction in CT20R was largely offset by the increased negative contribution by the direct dissipation effect of surface friction. Hence, it is necessary to compare the indirect and direct effects of surface friction in the full-physics model simulations.
Figure 8 compares the time evolutions of the vertically integrated energy gain rate from condensational heating and the rate of kinetic energy loss due to surface fiction, both averaged between 0.5 and 1.5 times the RMW in the simulated TCs in experiments CT20R and CT05R. The energy gain rate (J kg−1 s−1) and the rate of kinetic energy loss are calculated and converted from the volume-integrated condensational heating rate and vertical diffusion term (which includes surface friction)1 based on the model output, respectively. The difference in the energy gain rate from condensational heating between the two experiments can be regarded as the difference in the indirect effect of surface friction on TC intensification, whereas the difference in the rate of kinetic energy loss due to surface friction between the two experiments can be regarded as the difference in the direct dissipation effect of surface friction on TC intensification. Although the storm intensities in CT05R and CT20R are similar to each other until 60 h of simulation (Fig. 6a), the condensational heating rate (Fig. 8a) and the rate of frictional kinetic energy loss (Fig. 8b) are larger in CT20R than in CT05R. Because the storms in both experiments intensified synchronously, this again supports the idea that the increased positive indirect effect of surface friction is largely offset by the increased negative dissipation effect of surface friction in CT20R with larger CD. This explains why the simulated TC intensification rate during the primary intensification stage is insensitive to CD in numerical simulations of TCs.

Time evolutions of (a) the vertically integrated energy gain rate from condensational heating (J kg−1 s−1) and (b) the rate of kinetic energy loss due to surface friction (J kg−1 s−1) with a 5 h running mean, both averaged in the area between 0.5 and 1.5 times of the RMW in CT05R (blue) and CT20R (red) from 36 h to 60 h of simulations after CD was modified. The black (green) slashed area can be considered as the difference in the indirect (direct dissipation) effect of surface friction in the two experiments.
Since Sections 4.1 and 4.2 have demonstrated the insensitivity of the intensification rate of the simulated storm during the primary intensification stage, it is expected that the intensification rate of the simulated storm would be insensitive to different surface wind-dependent drag coefficients. To verify this point, two more experiments (CTDO and CTD1) with two different surface wind-dependent CD values given in (5) and (6) were conducted and compared with CTRL. The surface wind dependence of CD in the three experiments is illustrated in Fig. 1 (CTRL–black, CTDO–magenta, and CTD1–blue). The main difference between CTRL and CTDO is that the CD in CTRL is larger in the low-wind regime (below 15 m s−1) and smaller in the moderate-wind regime (between 15 m s−1 and 40 m s−1) and becomes larger again in the high-wind regime (above 40 m s−1). By contrast, the dependence of CTD1 is the same as that of CTDO when the 10-m height wind speed is below 30 m s−1 and remains constant with increasing wind speed and CD much larger than that in CTDO.
Figure 9 illustrates the time evolution of the maximum 10-m height azimuthal mean tangential wind speed and the corresponding intensification rate in CTRL, CTDO, and CTD1. Again, we see that the intensification rates during the primary intensification stage are very close to each other in the three experiments, confirming that the TC intensification rate during the primary intensification stage is insensitive to CD. Note that the durations of the initial spinup stages in CTDO and CTD1 are longer than that in CTRL because of the smaller CD in the low-wind regime in both CTDO and CTD1. This is consistent with the results for a storm with a smaller CD in CT05 compared with that in CT20. Note that the overall steady-state intensity of the simulated storm is weaker (stronger) in the experiment with larger (smaller) CD at the high-wind regime (Figs. 1, 9a). These results are consistent with those discussed in Section 4.1.
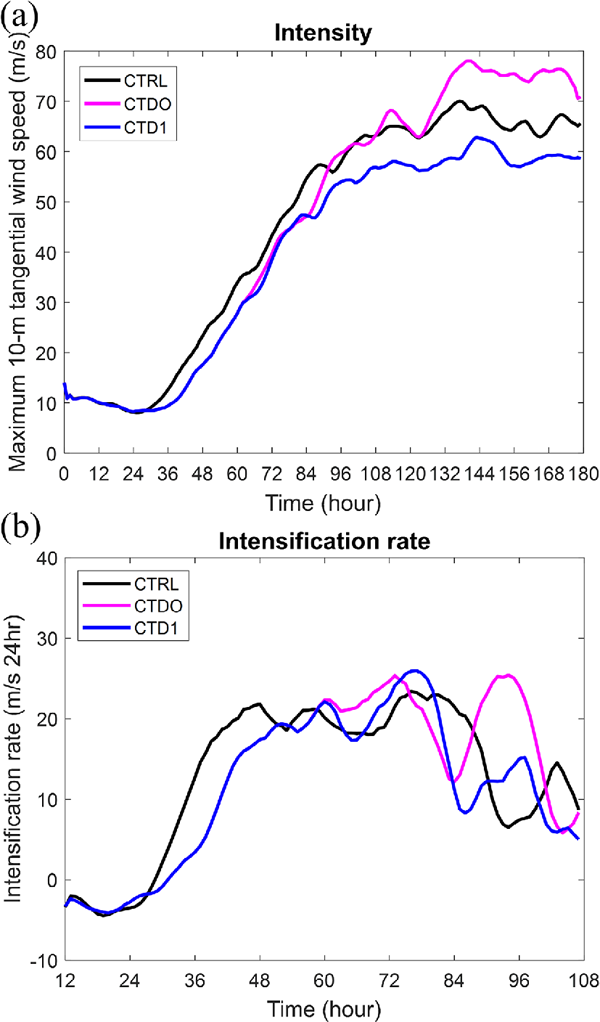
Same as Fig. 4, but for CTRL (black), CTDO (magenta), and CTD1 (blue).
Figure 10 illustrates the time evolutions of the vertically integrated energy gain rate from condensational heating and the rate of kinetic energy loss due to surface friction, both averaged between 0.5 and 1.5 times the RMW, in experiments CTRL versus CTDO and in CTDO versus CTD1. Since we attempt comparison of the rates of energy gain and energy loss for the storms with similar intensities in the pair experiments, different time periods are chosen, namely from 0 h to 30 h (46 h to 76 h in CTRL and 53 h to 83 h in CTDO) in Figs. 10a and 10c and from 60 h to 84 h in Figs. 10b and 10d. We can see that the storm in CTDO has a higher condensational heating rate and surface wind stress during the primary intensification stage than those of the storm in in CTRL (Figs. 10a, c). Indeed, CD is larger in CTDO when the surface wind speed is over 15 m s−1 (Fig. 1). The positive indirect effect due to a higher heating rate is largely offset by the negative dissipation effect of higher surface wind stress, leading to similar intensification rates of the simulated storms. Similarly, because CD in CTD1 is larger than that in CTDO in the high-wind regime (Fig. 1), the surface wind stress becomes larger in CTD1 than that in CTDO (Fig. 10d) after the 10-m height wind speed exceeds about 30–35 m s−1 (Fig. 9); even the storms in the two experiments have similar intensities (72 h). By contrast, larger CD at the high-wind regime in CTD1 also leads to higher condensational heating rate than that in CTDO (Fig. 10b). Again, the positive indirect effect due to the higher condensational heating rate is largely offset by the negative dissipation effect of higher surface wind stress in CTD1, leading to similar intensification rates of the simulated storms during the primary intensification stage.

Same as Fig. 8, but for (a), (c) CTRL (black) and CTDO (magenta) from 46 h to 76 h and 53 h to 83 h of simulations when the intensity is over 20 m s−1, respectively, and (b), (d) CTDO (magenta) and CTD1 (blue) from 60 h to 84 h of simulations.
Results from this subsection demonstrate that different dependencies of CD on surface wind speed can only change the duration of the initial spinup stage of the simulated TC. The intensification rates of the simulated TCs with different surface wind-dependent CD values during the primary intensification stage are similar because changes in the positive indirect and negative dissipation effects of surface friction largely offset each other, resulting in the insensitivity of the simulated TC intensification rate to the change in CD.
Figure 11 summarizes boundary layer processes that contribute to TC intensification in this study. The key processes are first investigated as a forced boundary layer response to a given radial distribution of gradient wind above the boundary layer using a boundary layer model. This helps quantify the dependence of the boundary layer response on CD (and thus surface friction). The results demonstrate that the boundary layer response of a TC vortex to a larger CD (and thus higher surface friction) is stronger and deeper boundary layer inflow. Meanwhile, more inwardly displaced larger radial mass convergence and stronger eyewall updraft appear inside the RMW together with a more inwardly displaced vorticity ring. This implies a faster contraction of the RMW and higher and more inwardly displaced condensational heating inside the RMW with higher inertial stability, which is favorable for a higher intensification rate of the TC vortex as expected from the balanced dynamics (e.g., Schubert and Hack 1982; Vigh and Schubert 2009). This is consistent with the finding by Frisius and Lee (2016), who demonstrated that it is the unbalanced nature of the boundary layer that leads to the occurrence of convective heating inside the RMW of a simulated TC and thus gives rise to a more rapid intensification than the simulation with a balanced boundary layer. The above sequential processes are similar to those hypothesized to explain the role of the boundary layer dynamics in the axisymmetric eyewall replacement cycle by Kepert (2013).

Schematic diagram summarizing the indirect effect of surface friction on TC intensification. The direction of the arrow represents the cause and effect. The blue dashed line denotes the RMW. The blue scalloped area denotes the predominant radial location of eyewall convection. There are four sequential interactive processes described in Section 5. The intensification rate of the storm can be attributed to changes in the radial distribution of gradient wind, which determines the strength and radial location of eyewall convection through the unbalanced boundary layer dynamics.
The full-physics model TCM4 is then used to investigate the TC intensification forced by condensational heating as a response of eyewall updraft/convection to boundary layer dynamics. Results indicate that large CD (and thus high surface friction) can considerably shorten both the initial spinup stage and the primary intensification stage of a simulated storm through the indirect effect of boundary layer dynamics. Previous studies have demonstrated that the duration of the initial spinup stage in numerically simulated TCs is determined by the rate of moistening in the inner-core region, which is largely controlled by moisture convergence in the inflow boundary layer and Ekman pumping at the top of the boundary layer and vertical mixing (Rotunno and Emanuel 1987; Emanuel 1989; Xu and Wang 2018). Results from the full-physics model TCM4 demonstrate that the inner-core region is moistened more rapidly in the case with larger CD. As the result from the boundary layer model indicates, larger CD tends to produce larger horizontal moisture convergence and stronger updraft inside the RMW, leading to faster moistening and initiation of eyewall convection and, thus, a shorter period of the initial spinup stage. However, large CD reduces the quasisteady intensity, which is consistent with the MPI theory (Emanuel 1988, 1997).
During the primary intensification stage, larger CD can induce stronger radial inflow together with higher and more inwardly displaced condensational heating inside the RMW, as predicted in the boundary layer model, contributing positively to TC intensification. However, a larger CD also induces a higher rate of frictional kinetic energy loss. The changes in the positive and negative effects due to change in CD in a reasonable range often offset each other during the primary intensification stage of a TC. As a result, the simulated TC intensification rate during the primary intensification stage is insensitive to CD in this study, as found in many previous studies.
In addition, results from the sensitivity experiments to surface wind speed-dependent CD confirm that different dependencies of CD on surface wind speed can change the duration of the initial spinup stage and the quasi-steady intensity of the simulated TC but have little effect on the intensification rate during the primary intensification stage of the simulated TC. Note that these conclusions are based on atmospheric model simulations only. With ocean coupling, increased surface stress due to larger CD may induce stronger upwelling and turbulent mixing at the mixed layer base and, thus, larger cooling in the mixed layer. This, in turn, may introduce a negative effect on TC intensification. Future studies should further examine the sensitivity by using a coupled ocean-atmospheric model.
In Part II, we demonstrate that the indirect effect of boundary layer dynamics in the presence of surface friction on TC intensification strongly depends on storm structure and intensity, whereas the (direct) dissipation effect of surface friction depends primarily on storm intensity. As a result, the intensification rate of a simulated TC during its primary intensification stage can be very sensitive to the structure of the initial TC vortex.
The authors are grateful to two anonymous reviewers for their constructive comments, which helped improve the manuscript. This study has been supported in part by the National Key R&D Program of China under grant 2017YFC1501602 and in part by NSF grants AGS-1326524 and AGS-1834300 and the National Natural Science Foundation of China under grant 41730960.
The rate of kinetic energy loss due to surface friction can be expressed by the volume-integrated time change in kinetic energy related to vertical diffusion terms (including surface friction) Fu and, i.e.,  , where V2 = u2 + v2, where Fu and Fv are the vertical diffusions of zonal and meridional winds, respectively.
, where V2 = u2 + v2, where Fu and Fv are the vertical diffusions of zonal and meridional winds, respectively.